基于三维地形修正的无线传感器网络覆盖盲区检测*

神显豪，李　军，奈　何（桂林理工大学信息科学与工程学院，广西桂林541004）



基于三维地形修正的无线传感器网络覆盖盲区检测*

神显豪*，李军，奈何
（桂林理工大学信息科学与工程学院，广西桂林541004）

摘要：三维地形下传感器节点经随机部署后，由于地形起伏的特点，会导致覆盖盲区的产生。为了能够有效检测覆盖盲区，本文提出了一种基于三维地形修正的无线传感器网络覆盖盲区检测方法，通过建立单位球感知模型，随机部署传感器节点，对节点进行Delaunay三角剖分。计算出三角形的外接圆，根据边界检测算法求出覆盖盲区边界，并且剔除假边界节点，得出改善后的边界。计算传感器节点的坡度和坡向信息，根据地形修正原理计算出传感器节点的实际探测半径，最终得出覆盖盲区的最小边界。仿真实验结果验证了该检测方法可有效检测三维地形下的覆盖盲区，对于起伏较大的地形也有一定的适应性。

关键词：覆盖盲区；三维地形修正；坡度和坡向；Delaunay三角剖分；外接圆

无线传感器网络WSN（Wireless Sensor Net⁃work）是由大量廉价的微型传感器节点随机部署在某一需要监测的区域，通过无线通信的方式自组织而形成的网络系统［1］。覆盖性能是衡量WSN服务质量的关键指标，不断改进和提高覆盖性能成为近年来研究的主要热点，覆盖盲区（或空洞）的修复是其中的一个重要研究内容。在目标区域中，传感器节点采用随机部署，导致部分监测区域没有传感器节点，从而出现覆盖盲区（或覆盖空洞），严重影响网络的性能。另外，随着网络的运行，传感器节点的能量耗尽也会导致覆盖盲区的形成。因此，当网络中出现覆盖盲区时，应该立即被检测到，维持WSN的完整性和可靠性［2］。

目前对于WSN覆盖盲区的研究，许多研究者提出了一些解决方法。如高昊，王庆生，冯秀芳等人［3］，提出一种基于几何图形的分布式覆盖盲区发现算法，该算法根据几何图形学的相关理论判断节点附近是否存在覆盖盲区；李明义，陈俊杰提出的无线传感器网络中覆盖空洞的检测算法［4］，根据无线传感器网络的覆盖空洞是由边界弧包围的，通过计算覆盖空洞的边界节点和边界弧，进而检测到覆盖空洞；戴国勇，陈麓屹，周斌彬等人提出的基于Voronoi图的无线传感器网络覆盖空洞检测算法［5］，该算法利用节点的位置信息在覆盖区域范围内构建Voronoi图，通过计算每个Voronoi区域内的节点到该区域的顶点和边的距离来判断是否存在覆盖空洞；邢冬平，段富，樊茂森提出的基于极坐标的无线传感器网络覆盖盲区发现算法［6］，该算法运用极坐标来表示节点之间的关系，通过几何算法来检测无线传感网络中是否存在覆盖盲区。上述的几种算法都属于二维平面的覆盖盲区检测方法，并不适用于三维地形。刘晔，傅忠谦［7］提出一种基于数字高程地图坡度信息的地形修正方法，通过构建传感器节点方向梯度感知模型，实现起伏地形下的陷阱空洞检测。但是该方法只适用于坡度变化平缓的三维起伏地形，对于起伏较大的三维地形并不适用。

在上述研究的理论基础上，本文针对更实际的三维起伏地形，提出了基于三维地形修正的WSN覆盖盲区检测方法，该方法能够有效的检测目标区域中的覆盖盲区。

1　覆盖盲区的形成

在WSN研究中，覆盖问题是基本问题之一，它影响到WSN的工作效率和质量。覆盖问题的核心是网络中传感器节点通过收集信息来实现对目标区域的监测和感知。通过合理的部署网络中的传感器节点，在保证满足相关的网络服务质量的要求下，最大程度的对监测区域进行覆盖。通常情况下，部署方式采取随机部署，传感器节点随机播散在目标区域中。然而这种方式很难一次把多个传感器节点的位置部署合理，导致网络覆盖不合理，最后形成感知重叠区和盲区［8］。如图1所示，二维平面的覆盖研究方法不能应用于三维平面，三维地形下的传感器节点经随机部署后，由于三维地形的起伏特点，会导致覆盖盲区的产生［9］。

由图1可知，投影到二维平面上的传感器节点实现了全覆盖。然而，传感器节点只能被放置在地表面，在三维地形表面上仍然存在覆盖盲区。

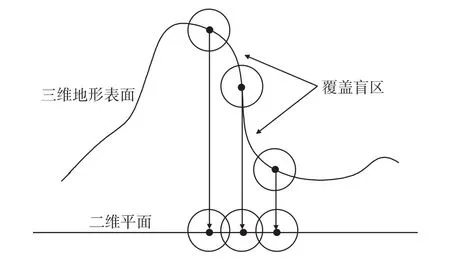
图1　覆盖盲区的截面图

2　网络模型与度量

2.1建立单位球感知模型

假设：目标区域是三维空间类的一个凸表面S，在笛卡尔积坐标系统中S可以表示为一个单值函数z=h(x，y)，当且仅当函数为z=c，c为常数时S为平面。一个传感器si被放置在目标区域S中，当传感器的坐标满足目标区域S的方程时，那么si∈S。

本文采用单位球感知模型，假设在三维的欧几里得空间中每个传感器的感知半径r都相同，每个传感器可以通过自己的感知范围感知和探测事件。这样感知区域形成了一个在三维空间中以si为中心，r为半径的球体。单位球模型的二维平面如图2所示。

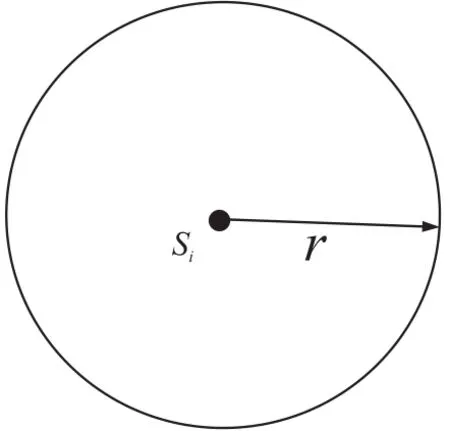
图2　单位球模型的二维平面

2.2传感器部署模型

传感器节点在目标区域的随机部署［10］，考虑了表面泊松点分布部署模型。假设n个传感器是均匀分布的，目标区域的面积S→∞，那么就能得到泊松分布的参数［11］：

那么m个传感器位于面积为G的传感器集合中的概率为：

2.3坡度与坡向的定义

坡度是三维地形表面陡缓的程度，通常把坡面的垂直高度和水平距离的比叫做坡度，即坡角的正切值。坡向是坡面法线在水平面上的投影的方向，亦高程下降最快的方向。三维地形表面上的传感器节点实际覆盖面可以等效成平面。在笛卡尔积坐标系中，通过AB线段为直径的圆来表示坡度和坡向，如图3所示。

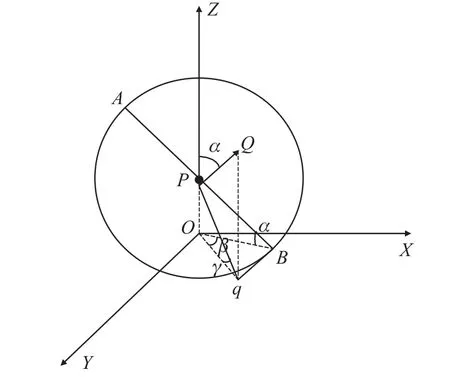
图3　AB段的坡度和坡向

其中，P点为三维凸曲面上的一点，PQ为AB段的法线，q为Q在XY平面上的投影，Oq为PQ在XY平面上的投影，α为法线PQ与Z轴的夹角，同时∠PBO=α，即坡度为I=tan α。β是Oq与OB的夹角，即坡向。γ为点P在β方向上的坡度。

通过GIS软件，从DEM地图数据中提取高程数据和坡度信息，在曲面z=h(x，y)上，对于点p(x，y)方向梯度为：

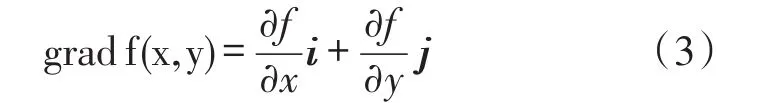
单位矢量，方向梯度的模为坡度。

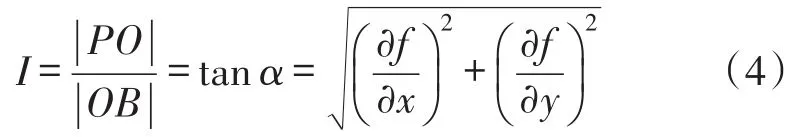
点P沿着β方向的坡度G为：

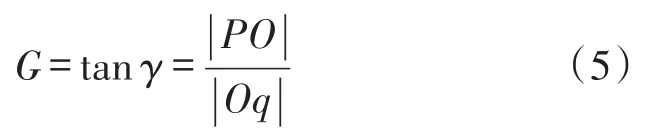
由式（4）、式（5）可知：

图3中，AB段为直径，即|AB|=2r。由于三维地形的起伏特点，传感器节点沿β方向的实际探测半径r’与理想探测半径r的关系可表示为：

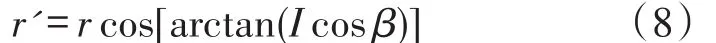
2.4地形修正原理

如图4所示，在50 m×50 m的区域中，随机部署40个传感器节点。图中给出了高程数值为100 到150的等高线。

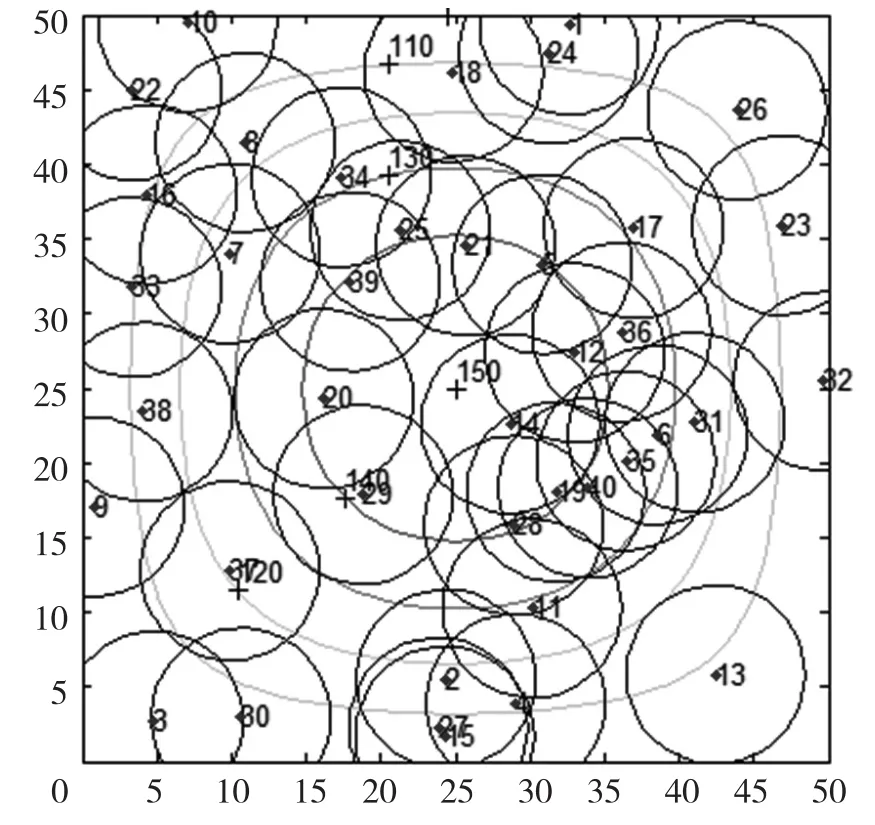
图4　地形修正原理

已知传感器节点坐标，可计算出每个节点的坡度和坡向角。沿着坡向方向，节点相交的两条等高线之间的差值，即高度差为Δh。相交的两条等高线之间的距离为Δd，那么坡度I可以表示为：

可以根据公式（8）算出实际探测半径。最终算出三维地形下每个传感器节点在二维平面上的椭圆投影，达到地形修正的目的。

2.5Delaunay三角形剖分

在目标区域内，以传感器节点为顶点对目标区域进行Delaunay三角剖分。假设V是二维实数域上的有限点集，e是点构成的封闭线段，e的集合为E。那么点集V的一个三角剖分T=(V，E)是一个平面图G，该平面图满足条件：①除端点外，平面图G中的边不包含点集V中的其他任何点。②没有相交边。③平面图G中所有的面都是三角面，并且所有三角面的合集是点集V的凸包。若存在一个圆经过V中a，b两点，并且圆内不含其他的点，则称ab边为Delaunay边。如果V的一个三角剖分T只包含Delaunay边，那么该三角剖分称为Delaunay三角剖分［12］。

2.6外接圆

每个Delaunay三角形的外接圆都是不包括其他Delaunay三角形的任何顶点的圆［13］。假定a，b，c 是Delaunay三角形的三条边，S是三角形的面积，（x，y）为外接圆的圆心，如图5所示。

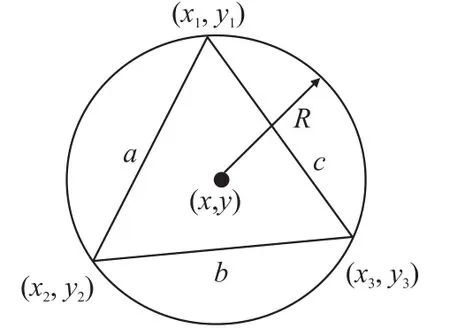
图5　外接圆

外接圆半径R表示为：

Android操作系统维护着自己的一套事件分发机制，Android应用程序、触发事件和后台逻辑处理，都是根据该机制一步步向下执行，恶意软件的敏感行为也不例外。若能在事件传送到终点前将事件截获并对其操作进行一定修改，就可以有效地抑制恶意行为的效果，这就是Hook机制。

假定三条边的坐标分别是（x1，y1），（x2，y2），（x3，

y3），那么外接圆的圆心坐标（x，y）可表示为：

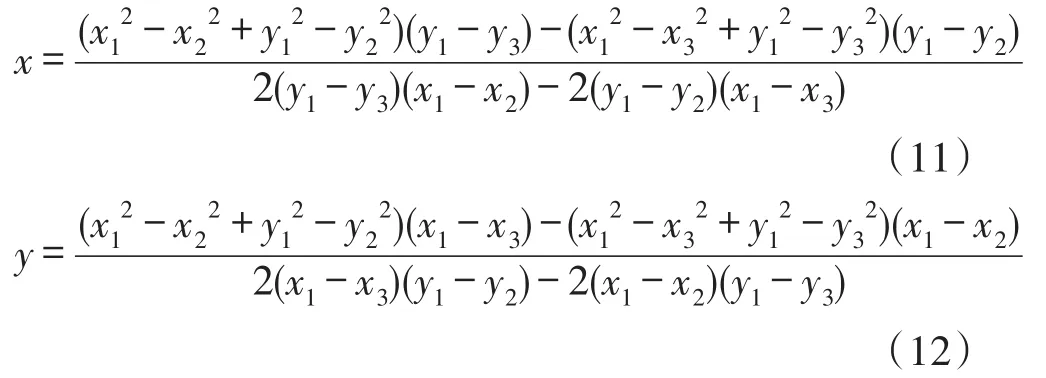
2.7边界节点和假边界节点

在覆盖盲区的边界上，能够包围覆盖盲区的节点称为边界节点［14］。然而这些边界节点中存在着假边界节点。假定覆盖盲区边界中Delaunay三角形的三个顶点分别是S1，S2，S3，如图6、图7所示。

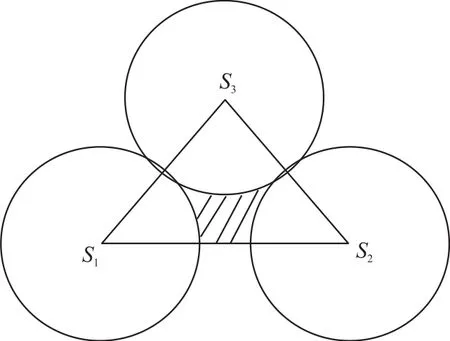
图6　边界节点

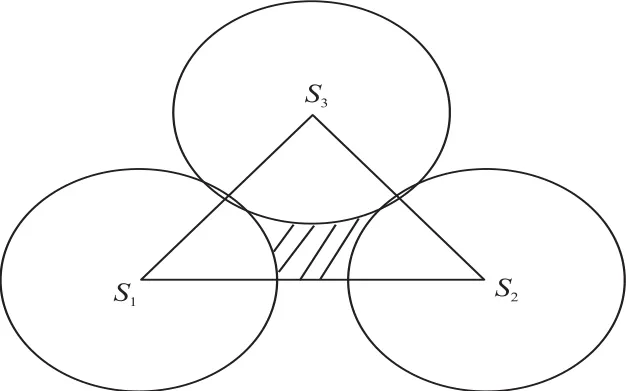
图7　假边界节点

因为覆盖盲区是在Delaunay三角形之外的部分，图6中存在部分区域未被任何节点覆盖，如阴影部分所示，所以S1，S2，S3都是边界节点。然而图7 的Delaunay三角形中没有未被覆盖的区域，所以S1和S2节点是边界节点，而S3是假边界节点。

假边界节点的判定如下：假设S1，S2，S33个节点的感知半径为r，外接圆的圆心为Oc，外接圆半径为R。图中O1为S1和S3的垂直平分线与S2的交点，同理O2为S2和S3的垂直平分线与S1和S2的交点，直线S3O3垂直于直线S1S2，如图8所示。如果S3O1>r或者S3O2>r，那么在ΔS1S2S3中肯定存在一些覆盖盲区。如果S3O1>r、S3O2>r并且S3O3<=r，那么在ΔS1S2S3中存在两个分离的覆盖盲区。

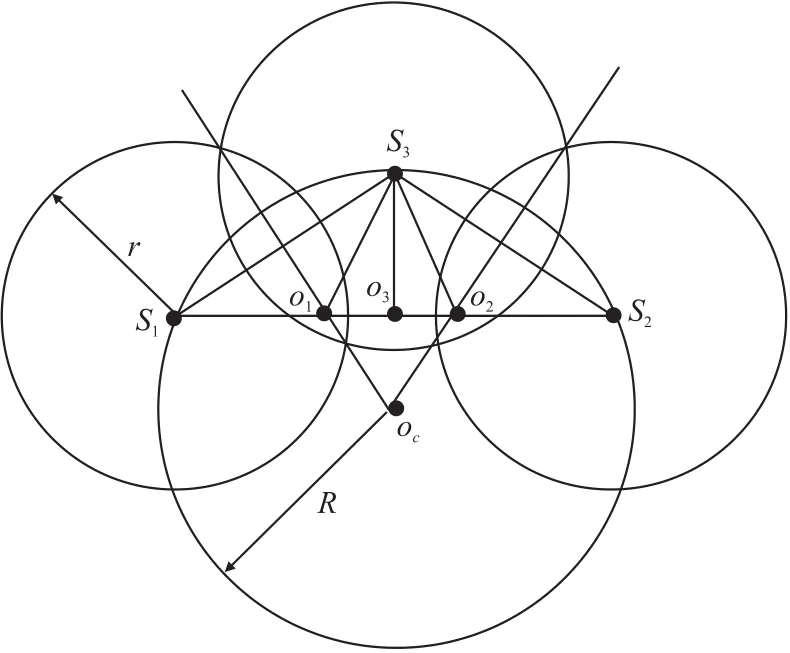
图8　假边界节点的判定

对于外接圆圆心在Delaunay三角形外面并且R>r的边界节点，利用假边界节点的判定方法，判断Delaunay三角形内部是否被节点全覆盖。如果Delaunay三角形中不存在覆盖盲区，那么Delaunay三角形中最长边对应的节点为假边界节点。

3　覆盖盲区的检测算法和地形修正

传感器节点随机部署在目标区域中，可能会存在覆盖盲区。通过Delaunay三角形剖分算法对传感器节点中心点进行三角形划分。根据每个De⁃launay三角形的坐标来算出自身的外接圆。假设传感器节点半径为r，每个外接圆的半径为R，相邻两个Delaunay三角形的公共边长为d，检测算法如下：①将N个传感器节点随机部署在目标区域中，对每个节点的中心点进行Delaunay三角形剖分。②做出每个Delaunay三角形的外接圆。比较节点半径和外接圆半径，如果R>r，那么肯定存在覆盖盲区，保存下这个Delaunay三角形和外接圆，否则去掉外接圆。③计算剩余两个相邻三角形的公共边长d。如果d>2r，或者公共边不与两个三角形外接圆的中心连线相交，那么对这些三角形进行聚类分组得到边界节点，每个聚类分组都会存在覆盖盲区。④对每个聚类分组中的传感器节点（边界节点）中心点，用能够包含覆盖盲区的最小多边形的方法，表示出覆盖盲区边界。⑤对边界节点进行假边界节点的判定，去掉假边界节点之后，再次用能够包含覆盖盲区的最小多边形方法，表示出覆盖盲区的边界。⑥由于三维地形的起伏特点，传感器节点随机部署在目标区域的实际覆盖面积会变小，经过地形修正的传感器节点的二维覆盖区域为椭圆。利用坡度和坡向角算出实际半径，最后使用检测算法求出修正后的覆盖盲区边界。

4　仿真评估

4.1表面的生成

论文采用MATLAB 2012b仿真平台来进行仿真。为了表示表面的覆盖性能，我们用单值函数z=h(x，y)，来表示生成的表面。

其中x和y∈［0，50］，系数C=1，2，3时生成曲面。在［0，50］×［0，50］m的区域中，曲面有1，4，9个顶峰和低谷。图9~图11为曲面的等高线，单位为米。图中标注了每条等高线的数值。

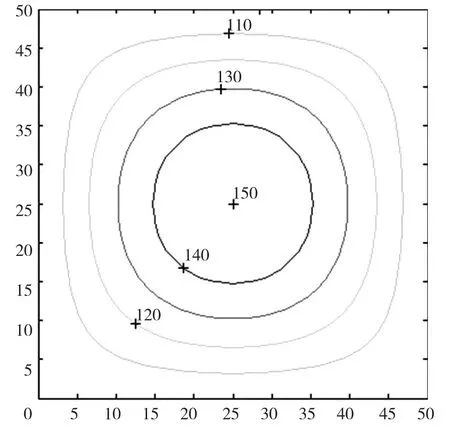
图9　C=1时的等高线

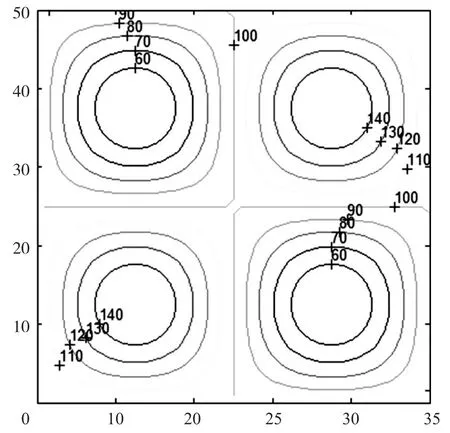
图10　C=2时的等高线

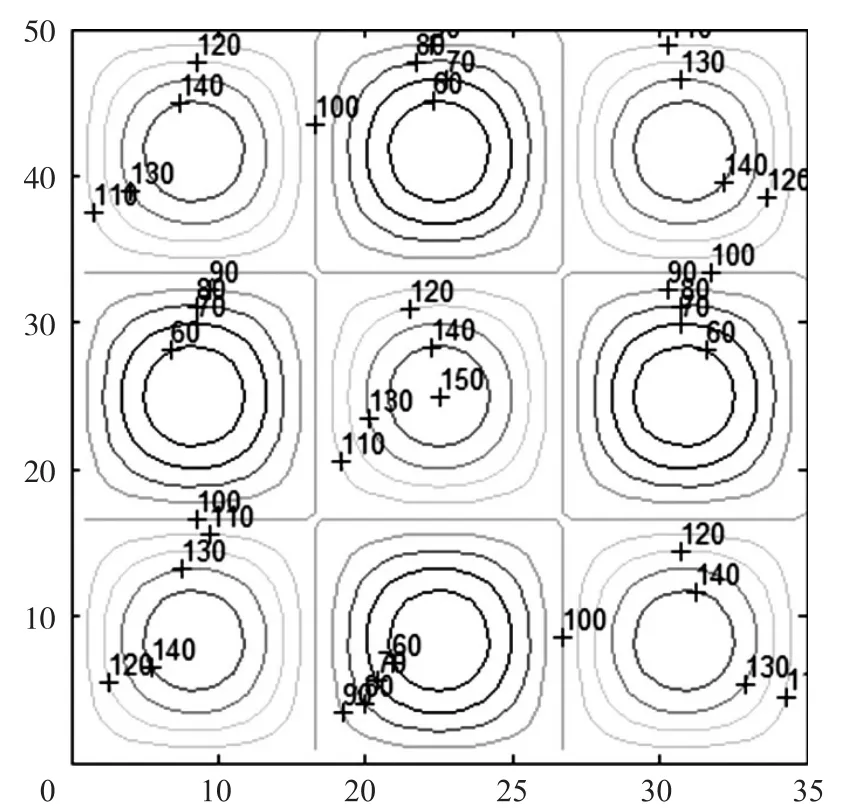
图11　C=3时的等高线

4.2仿真结果对比

假设在50 m×50 m的区域内，随机部署的传感器节点数N=40，节点的理想探测半径为r=6。每个Delaunay三角形的外接圆半径为R。仿真参数如表1所示。对40个传感器节点的中心点进行Delaunay三角剖分，可以得到多个Delaunay三角形。如图12所示。其中圆形区域表示节点的覆盖区域。

表1　仿真参数

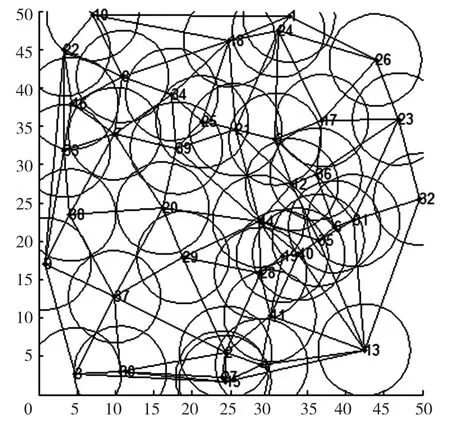
图12　Delaunay三角剖分

已知Delaunay三角形的顶点坐标，可以求出每个三角形的外接圆半径R和外接圆心。如图13所示，如果R>r时，表示存在覆盖盲区。

图13　Delaunay三角形的外接圆

根据覆盖盲区边界的检测算法，对符合条件的Delaunay三角形进行聚类分组。分组得到多个边界节点之后，用能够包含覆盖盲区的最小多边形的方法来表示出覆盖盲区的边界，如图14所示。

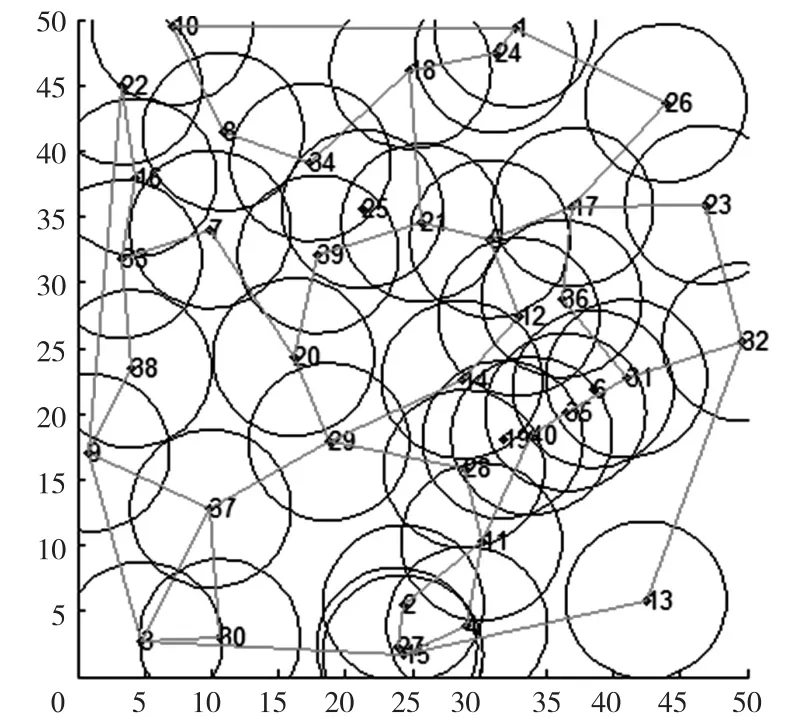
图14　覆盖盲区的边界

去掉边界节点中存在的假边界节点，得出改善的盲区边界。如图15所示。

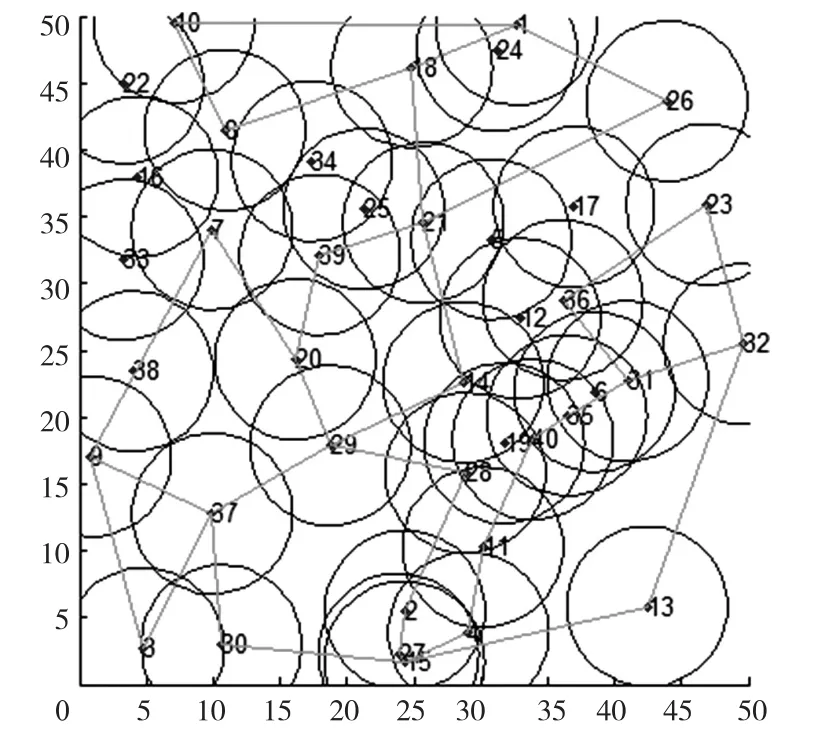
图15　去掉假边界节点后的边界

根据地形起伏程度，如表2所示，设置了3种地形。对三维起伏地形进行地形修正之后，得出覆盖盲区边界。

表2　地形参数

在地形I，II，III的情况下，地形修正后覆盖盲区的边界如图16~图18所示。

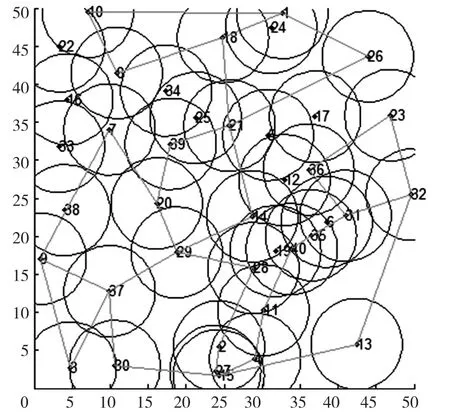
图16　地形I的修正结果

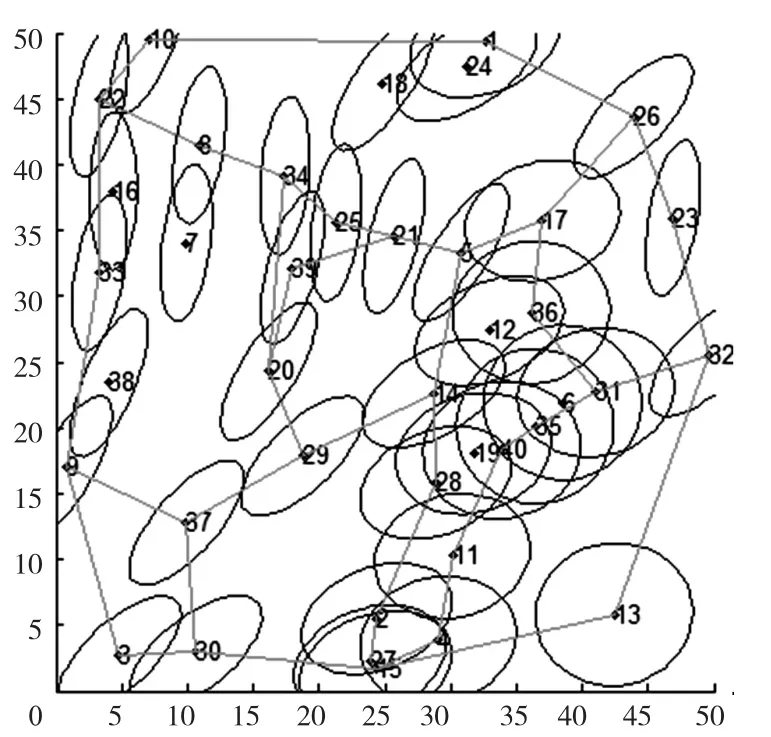
图17　地形II的修正结果

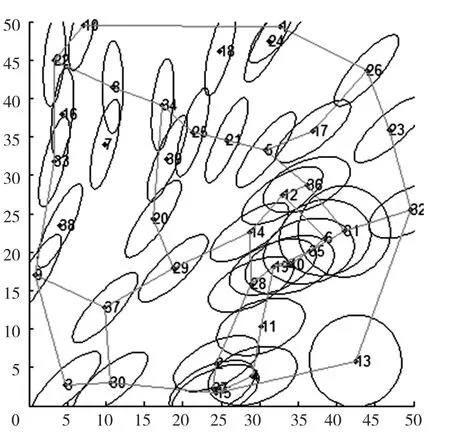
图18　地形III的修正结果

在区域范围相同、节点数目相同的情况下，随着顶峰和低谷数增加，地形起伏程度逐渐增大。由上述地形I、地形II和地形III修正结果对比可知，随着地形起伏程度增大，盲区面积逐渐增大，导致覆盖边界逐渐增大，WSN的覆盖率逐渐下降。仿真结果表明，该结果在起伏较大的地形情况下同样适用。

为了进一步评价三维地形修正方法的性能，在相同的仿真实验条件下，与未去掉假边界节点的传统修正方法［7］进行对比，其中“平面”表示传感器节点随机部署后未进行地形修正的覆盖率，仿真对比如图19所示。

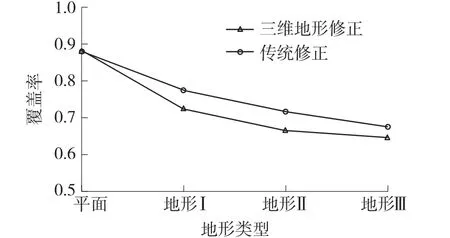
图19　与传统修正方法的仿真对比

由图19可知，传统修正方法和三维地形修正方法随着地形起伏程度增大，经地形修正后的覆盖率均逐渐下降。三维地形修正方法在三种地形下的覆盖率均低于传统修正方法，说明它能检测出目标区域中更多的覆盖盲区。因此，三维地形修正方法对覆盖盲区的检测效果更好，更适用于起伏较大的三维地形。

5　结论

对于三维地形起伏的特点，本文提出了一种基于三维地形修正的WSN覆盖盲区检测方法。通过覆盖盲区边界检测算法，求出目标区域的覆盖盲区边界，经过地形修正后得出最终的覆盖盲区边界。仿真实验结果表明，地形修正后的覆盖盲区边界明显变大，该结果在三维起伏较大的地形条件下得出，对三维起伏地形下的传感器节点部署具有参考价值。

参考文献：

［1］王伟，林锋，周激流.无线传感器网络覆盖问题的研究进展［J］.计算机应用研究，2010，27（1）：32-35.

［2］胥楚贵，邓晓衡，邹豪杰.无线传感器网络覆盖空洞修复策略［J］.传感技术学报，2010，23（2）：256-259.

［3］高昊，王庆生，冯秀芳，等.无线传感器网络中覆盖盲区发现算法［J］.传感器与微系统，2012，31（9）：109-115.

［4］李明义，陈俊杰.无线传感器网络中覆盖空洞的检测算法［J］.计算机测量与控制，2013，21（9）：2501-2505.

［5］戴国勇，陈麓屹，周斌彬，等.基于Voronoi图的无线传感器网络覆盖空洞检测算法［J］.计算机应用，2015，35（3）：620-623.

［6］邢冬平，段富，樊茂森.基于极坐标的无线传感器网络覆盖盲区发现算法［J］.传感器与微系统，2014，33（9）：117-119.

［7］刘晔，傅忠谦.基于地形修正的无线传感器网络陷阱空洞检测［J］.传感技术学报，2014，27（6）：785-790.

［8］Xiao Yang L，Kai Liang W，Yanmin Z，et al. Mobility Increases the Surface Coverage of Distributed Sensor Networks［J］. Comput⁃er Networks，2013，57：2348-2361.

［9］刘志坤，夏清涛，罗浩.无线传感器网络三维覆盖策略研究［J］.武汉理工大学学报（交通科学与工程版），2013，37（3）：581-584.

［10］李猛，丁代荣，郭廷立.一种无线传感器网络节点随机部署策略［J］.计算机工程，2012，38（5）：99-101.

［11］徐奕昕，白焰，赵天阳，等.泊松分布下无线传感器网络多目标覆盖控制［J］.计算机应用，2013，33（7）：1820-1824.

［12］余杰，吕品，郑昌文. Delaunay三角网构建方法比较研究［J］.中国图象图形学报，2010，15（8）：1158-1167.

［13］Hwa Chun M，Prasan Kumar S，Yen Wen C. Computational Geom⁃etry Based Distributed Coverage Hole Detection Protocol for the Wireless Sensor Networks［J］. Journal of Network and Computer Applications，2011，34：1743-1756.

［14］Wei L，Wei Z. Coverage Hole and Boundary Nodes Detection in Wireless Sensor Networks［J］. Journal of Network and Computer Applications，2015，48：35-43.

神显豪（1980-），男，广西南宁横县人，博士，桂林理工大学副教授，主要研究方向为智能故障诊断、无线传感器网络，lyj_sxh@sina.com；

李军（1990-），男，安徽滁州市人，桂林理工大学硕士研究生，研究方向为无线传感器网络，leejun19901113@163.com；

奈何（1992-），男，湖北省襄阳市人，桂林理工大学硕士研究生，研究方向：无线传感器网络，985515263@qq.com。

Research on the Capacity of Wireless Networks Based on the Network Coding*

MENG Limin*，ZHANG Jing，ZHOU Kai，YING Songxiang
（College of Information Engineering，Zhejiang University of Technology，Hangzhou 310023，China）

Abstract：The network capacity has been a hotspot in the field of wireless network. Network coding has the advan⁃tage that the intermediate node can encode the data it receives，which can efficiently improve end-to-end through⁃put. In this paper，we first analyze the multi-hop capacity of wireless network based on the signal-to-interference ra⁃tio model proposed by Gupta. Then an algorithm of wireless network capacity based on the network coding is pro⁃posed and to compute the upper bound of the network capacity，we obtain the network maximum flow and each link flow by utilizing the method which solves linear programming problems in the MATLAB. The simulation experi⁃ments show that the capacity using network coding is higher than that of traditional routing strategy and the upper bound of network capacity has a trend of first increasing and then decreasing with the number of nodes.

Key words：wireless network；network capacity；network coding；max-flow min-cut theorem

doi：EEACC：723010.3969/j.issn.1004-1699.2016.01.020

收稿日期：2015-08-12修改日期：2015-09-20

中图分类号：TP393

文献标识码：A

文章编号：1004-1699（2016）01-0109-07

项目来源：国家自然科学基金项目（E050603）；广西高等学校科研项目（YB2014157）；广西自然科学基金项目（2015GXNSFBA139254）