多准则MEMS陀螺随机误差在线建模与实时滤波*

代金华，张丽杰（.内蒙古工业大学信息工程学院，呼和浩特0005；2.内蒙古工业大学电力学院，呼和浩特0005）



多准则MEMS陀螺随机误差在线建模与实时滤波*

代金华1，张丽杰2*
（1.内蒙古工业大学信息工程学院，呼和浩特010051；2.内蒙古工业大学电力学院，呼和浩特010051）

摘要：针对随机误差相关性较弱的MEMS陀螺仪，提出采用多准则曲线方法辨识其带有截距项的随机误差时间序列模型。采用该模型可直接对MEMS陀螺仪的实测量数据进行在线建模，而无需零均值化离线处理。基于该模型并采用状态扩增的方法设计卡尔曼滤波器，实现了MEMS陀螺仪随机误差的实时滤波。实验结果表明，针对某MEMS陀螺仪带有截距项的AR（2）模型可以作为其随机误差模型，经过在线建模和实时滤波后，MEMS陀螺仪随机误差的标准差降低了50%，有效抑制了MEMS陀螺仪的随机误差。

关键词：MEMS陀螺仪；时间序列模型；在线建模；卡尔曼滤波

MEMS（Micro-Electro-Mechanical Systems）陀螺仪具有成本低、尺寸小、重量轻、可靠性高等优点，在低成本惯性系统中获得越来越广泛的应用。但是MEMS陀螺仪的测量精度等性能指标却远低于传统的陀螺仪，制约了其在高精度姿态控制中的应用［1-2］。通过对MEMS陀螺仪随机漂移误差信号进行有效的建模和补偿来提高测量精度的方法越来越受到重视［3］。常用的MEMS陀螺仪随机误差建模方法包括神经网络技术、小波分析、时间序列法、一阶高斯—马尔柯夫随机过程等［4-5］。神经网络和小波分析随机误差建模方法得到的模型通常具有较高的阶次，并不十分适合于低成本系统随机误差的实时在线估计［6-9］。采用一阶高斯—马尔可夫随机误差建模方法的缺点是由于自相关序列判定的不精确带来惯性敏感器随机误差建模的不精确［10-11］。时间序列分析法直接对随机序列建立差分方程，与一阶高斯—马尔可夫过程相比，其具有更好的建模灵活性和稳定性，计算得到的参数值不会随着样本长度的改变而改变。对MEMS陀螺仪随机漂移误差信号进行时间序列建模和补偿来提高测量精度的方法越来越受到重视［12］。

本文以实验室已开发的MIMU模块的角速率测量输出为实验对象［13］，研究基于时间序列分析的误差建模和补偿方法。提出采用多准则曲线方法辨识MEMS陀螺仪随机误差的时间序列模型，该模型不要求对序列进行零均值化预处理，将序列均值作为一个未知参数，在ARMA模型中加上一个截距项，以保证建模的准确性和实时性。采用该模型可直接对MEMS陀螺仪测量噪声进行在线建模，进而基于该模型并采用状态扩增的方法设计卡尔曼滤波器，可使滤波器对数据无零均值要求，有效减小MEMS陀螺仪的随机误差。

1　MEMS陀螺仪随机误差的时间序列模型

1.1具有截距项的时间序列模型

时间序列ARMA（p，q）模型要求信号为平稳、正态分布和零均值时间序列。统计检验证明MEMS陀螺仪测量输出数据可以看作平稳、正态时间序列，但是由于其零偏的存在，需要离线进行零均值化预处理才能建模。为了可以直接对MEMS陀螺仪静态输出信号在线建模，本文考虑将MEMS陀螺仪随机序列的均值μ作为模型的一个未知参数。

平稳、正态、非零均值时间序列｛Xt｝的ARMA（p，q）模型可写为［14］：

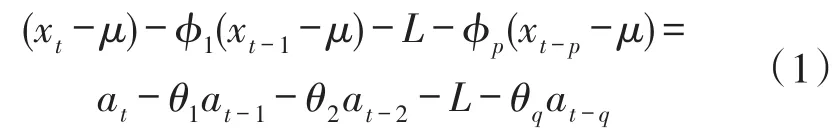
其中，ϕ1，ϕ2，L，ϕp称为自回归参数，θ1，θ2，L，θq称为滑动平均参数，μ是时间序列{Xt}的均值。若滑动平均参数为零，则ARMA（p，q）变为AR（p）模型；若自回归参数为零，则ARMA（p，q）变为MA（q）模型。

式（1）可变形为

令c=(1-ϕ1-ϕ2-L-ϕp)μ，则式（2）可写为，

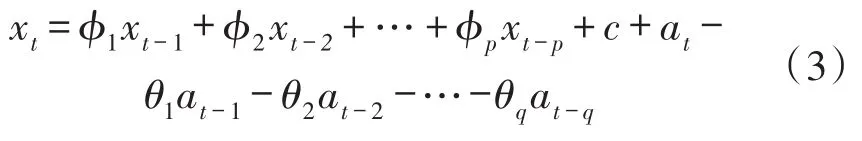
由式（3）可知，序列均值对模型的影响体现在多了一个参数c。因此，在MEMS陀螺仪随机误差模型识别阶段，可对其随机误差序列的均值是否为零不予考虑，只需给ARMA模型增加一个截距项，在参数估计阶段进行在线估计即可，从而保证建模实时性。

1.2基于相关性分析的MEMS陀螺仪随机误差模型辨识

通常，可依据随机序列自相关函数（ACF）和偏相关函数（PACF）的“拖尾”和“截尾”性质辨识时间序列的模型结构（ARMA、AR、MA）［14］。自相关函数和偏相关函数特性见表1。

表1　自相关函数和偏相关函数特性

对MEMS陀螺仪进行相关性分析，结果如图1所示。由图1可知，MEMS陀螺仪随机误差序列的ACF和PACF都具有1阶截尾特性，无法判断其属于哪种时间序列模型结构。产生这种现象的原因是MEMS陀螺仪的随机序列相关性较弱，因此不能完全依据ACF和PACF“拖尾”和“截尾”的性质来判定MEMS陀螺仪随机序列的模型结构及阶次，还需采用其他方法进行模型的识别。

图1　陀螺的自相关和偏相关

2　MEMS陀螺仪随机误差模型的多准则曲线辨识

2.1多准则曲线辨识性能函数的定义

常用的时间序列模型辨识方法包括AIC准则、BIC准则、FPE准则以及残差值等［13］。不同准则对拟合残差与参数个数之间进行不同的权衡，因此不同准则挑选出的最优模型，其渐进性是不同的［14］。为了减小建模误差，提高误差补偿精度，本文取残差方差>、FPE函数、AIC函数、BIC函数同时达到最小时的p，q值作为适用模型的阶数。定义此时的性能函数为

J(p，q)=min(FPE(p，q)，AIC(p，q)，BIC(p，q)，)（4）由式（3）可知，MEMS陀螺仪时间序列模型含有p+ q+1个参数，因此需将、AIC函数、BIC函数、及FPE函数的计算公式改为

其中，N为观测序列样本个数。考虑到函数曲线的直观性，可根据多个准则函数的曲线趋势直接确定J取最小值时阶次p和q的值。

2.2多准则曲线辨识模型的步骤

根据式（3）和式（4），MEMS陀螺仪的ARMA（p，q）模型的多准则曲线辨识模型的步骤如下，

①设定一个合适的模型阶数上限值L。通常MEMS陀螺仪的时间序列模型的阶数较低，一般不超过3阶，对于实际的随机系统，随机ARMA模型的自回归阶数大于或等于滑动平均阶数［15-16］，并且通过ARMA模型和AR模型辨识可以间接确定MA模型是否合适，所以仅需针对ARMA模型和AR模型进行辨识。

②依据式（3），采用最小二乘法估计参数

ϕ1，ϕ2，L，ϕp，c，θ1，θ2，L，θq(0≤p≤L，0≤q≤L)。

④对随机误差模型进行适用性和显著性检验。若残差序列为白噪声序列说明该拟合模型能够提取观测序列中几乎所有的样本相关信息，说明该拟合模型是适用的［14］；显著性检验是通过假设检验方法［14］，检验模型参数是否显著非零，剔除不显著的参数所对应的变量，达到精简随机误差模型的目的。

3　卡尔曼滤波器的设计

根据式（3）带有截距项的ARMA（p，q）模型，采用状态扩增法设计卡尔曼滤波器，将截距项c也列为状态，对其进行在线估计，则可直接对MEMS陀螺仪的实测信号进行卡尔曼滤波。

不妨以ARMA（2，1）为例（其他阶次模型同理），扩增状态后的系统状态方程和测量方程可表示为

其中，扩增后的状态变量Xk=[xkxk-1c]T，系统过程噪声，系数矩阵，Vk是测量误差，Wk和Vk为互不相关的零均值白噪声序列。

Xk的估计量可以根据以下卡尔曼滤波递推方程求解：

状态的一步预测方程为

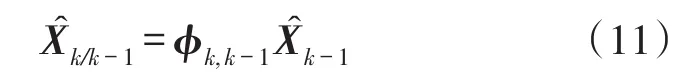
滤波状态估计方程为

滤波增益方程为

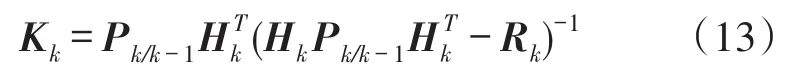
估计协方差阵的一步预测方程为

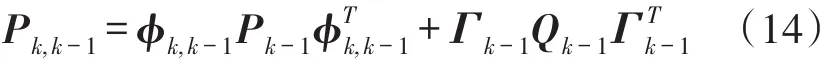
估计协方差阵的更新方程为

状态变量初始值X0选为角速度测量序列的初值；实际测量数据作为观测量Ζk，其协方差为测量噪声的正定方差阵Qk，经过ARMA模型拟合后的残差信号的协方差为系统噪声协方差阵Rk，随机误差序列的方差作为初始误差协方差阵P0。

4　实验验证

为了验证误差模型的准确性和滤波器的有效性，针对实验室研制的无人机项目中应用的MIMU模块进行了实验，该MIMU模块包括：3个单轴陀螺ADXRS610，其灵敏度是6 mV/（°/s），噪声密度是一个三轴MEMS加速度计MMA7260，其灵敏度是800 mV/gn（1.5 gn），噪声密度是4.7 mV/（rms）［13，17］。

在室温条件下，首先加电预热60 min，利用STM32F103MCU采集陀螺仪的静态角速率输出，且外部转台输入量为零。此处仅给出单轴陀螺仪的实验结果。

4.1多准则曲线模型辨识实验

4.1.1定阶和参数估计

对于ARMA（p，q）模型，取L=2，即0≤p≤2，0≤q≤2；对于AR（p）模型，取L=5，即0≤p≤5。以100 Hz采样频率采集并保存1min的测量输出数据，进行离线分析。分别作出AR模型和ARMA模型的、FPE函数、AIC函数和BIC函数的曲线，如图2所示，其中图2（a）中的横坐标为1和2时分别表示ARMA（1，1）和ARMA（2，1）模型的和FPE、AIC、BIC函数的值。根据不同准则的数量级和相应曲线的变化趋势，将AIC和BIC准则的曲线绘制在一张图上，将和FPE准则的曲线绘制在一张图上。

图2　陀螺仪的AR模型和ARMA模型的多准则函数曲线

采用最小二乘法估计得到的AR（2）模型和ARMA（1，1）模型见表2。

表2　陀螺时间序列模型

4.1.2随机误差模型的适用性和显著性检验

利用Matlab中的函数lbqtes对表2中的模型残差序列进行Q检验可知，模型残差序列不具有相关性，满足白噪声序列的要求，即AR（2）模型和ARMA（1，1）模型是适用的。

临界值取标准正态分布的上侧a=0.025分位数1.96，对于表2中的模型进行参数的显著性检验，t检验的结果见表3。

表3　模型参数的显著性检验

由表3可知，ak-1项对模型影响很小，剔除该项后，ARMA（1，1）模型精简为AR（2）模型，则参数显著性检验结果可确定MEMS陀螺仪的随机误差模型为

4.2卡尔曼滤波实验

根据4.1得到的AR（2）模型结构，编写在线建模和卡尔曼滤波程序。

卡尔曼滤波递推方程中状态变量初值X0=[x2x1c]T，其中x1，x2是角速率测量输出序列的前两个值。估计协方差阵初值

将MEMS陀螺仪的静态输出信号直接作为上述卡尔曼滤波器的输入，在前2 min内完成建模，然后开始滤波。

图3　陀螺仪的静态测量数据卡尔曼滤波

表4　卡尔曼滤波前后陀螺数据的均值和标准差

陀螺仪测量输出数据卡尔曼滤波结果如图3，滤波前后的数据均值和标准差见表4。由图3和表4可知，陀螺静态输出信号曲线的均值没有明显改变，但标准差减小了50%。说明卡尔曼滤波可以有效降低陀螺的随机噪声，从而验证了将具有均值估计的AR（2）随机误差模型用于滤波算法对于减小噪声是有效的，同时说明将信号均值作为卡尔曼滤波状态变量也是合理的。

5　结论

为了解决MEMS陀螺仪零偏影响随机误差建模实时性的问题，本文将信号的均值作为时间序列模型中的一个参数进行估计，同时针对随机误差序列的相关性较弱的MEMS陀螺仪，本文提出了一种多准则曲线辨识方法对MEMS陀螺仪的随机误差模型进行辨识。并在此基础上设计卡尔曼滤波器，对MEMS陀螺仪的测量输出进行随机误差补偿。实验结果表明，具有截距项的AR（2）模型适合用作MEMS陀螺仪随机误差序列的数学模型，用在线得到的参数值直接进行卡尔曼滤波，可以有效降低信号的噪声。

参考文献：

［1］房建成，张霄，李建丽.一种MEMS陀螺标度因数误差补偿方法［J］.航空学报，2010，31（2）：350-355．

［2］徐定杰，苗志勇，沈锋，等. MEMS陀螺随机漂移误差系数的动态提取［J］.宇航学报，2015，36（2）：217-223．

［3］Ren B，Zhang D M，Li H. MEMS Gyroscope Random Error Model⁃ing and Filtering［J］. Applied Mechanics and Materials，20l0，29-32：829-834.

［4］杨庆辉，杜红英，陈雄，等.微机电陀螺随机漂移建模与卡尔曼滤波［J］.计算机仿真，2015，32（3）：68-72．

［5］蔡雄.硅微机械陀螺仪的随机误差建模与补偿［D］.南京：南京理工大学，2011．

［6］Minha P，Yang G. Error and Performance Analysis of MEMS Based Inertial Sensors with a Low-Cost GPS Receiver［J］. Sen⁃sors，2008，8（4）：2240-2261．

［7］吉训生，王寿荣. MEMS陀螺仪随机漂移误差研究［J］.宇航学报，2006，27（4）：640-642．

［8］何昆鹏. MEMS惯性器件参数辨识及系统误差补偿技术［D］.哈尔滨：哈尔滨工程大学，2009．

［9］袁赣南，梁海波，何昆鹏，等. MEMS陀螺随机漂移的状态空间模型分析与应用［J］.传感技术学报，2011，24（6）：853-858.

［10］Chen D K，Hart J Q. Application of Wavelet Neural Network in Sigma Processing of MEMS Accelerometers［J］.Microsystem Tech⁃nologies，2011，17（1）：l-5．

［11］王浩，黄长强，王勇，等.基于自回归过程的惯性敏感器随机误差建模［J］.中国惯性技术学报，2008，16（2）：224-227．

［12］姜宇，金晶，张迎春，等.基于异方差分析的多MEMS陀螺随机误差补偿方法［J］.宇航学报，2012，33（6）：776-780．

［13］张丽杰，常佶.小型飞行器MEMS姿态测量系统［J］.振动测试与诊断，2010，30（6）：698-704.

［14］王振龙.应用时间序列分析［M］.北京：中国统计出版社，2010：132-133．

［15］蒙涛，王昊，李辉，等. MEMS陀螺误差建模与滤波方法［J］.系统工程与电子技术，2009，31（8）：1944-1948．

［16］李杰，张文栋，刘俊，等.基于时间序列分析的Kalman滤波方法在MEMS陀螺仪随机漂移误差补偿中的应用研究［J］.传感技术学报，2006，19（5）：2215-2219．

［17］张丽杰，常佶.微小型航姿测量系统及其数据融合方法［J］.中国惯性技术学报，2011，19（3）：307-311．

代金华（1980-），女，蒙古族，内蒙古赤峰人，硕士，讲师，研究方向为检测与控制、导航等，djh19@126.com；

张丽杰（1973-），女，辽宁省康平县人，博士，副教授，研究方向为检测与控制、导航等。

Energy-Consumption Balancing Routing Protocol Based on Regions*

ZHAI Chunjie1，XU Jianmin2，LIU Yonggui1*
（1.School of Automation Science and Engineering，South China University of Technology，Guangzhou 510641，China；2.School of Civil Engineering and Transportation，South China University of Technology，Guangzhou 510641，China）

Abstract：An energy-consumption balancing routing protocol based on regions is proposed to balance the energy consumption of wireless sensor network and enhance the network stability. The protocol designs an optimized regiondivided algorithm which divides sensor nodes into clusters based on the regions to solve the random problem of clus⁃ters’number and distribution in previous protocols. In selecting clusters，a three-level selectional mechanism of clus⁃ter heads is adopted after taking consideration the factors of the residual energy of sensor nodes，the cluster topology and the internal total energy consumption of cluster. In forwarding the data，general nodes can choose the nearest cluster head which can select the next hop one in a two-upper level within the threshold of communication distance. Simulation results suggest，compared with DREEM-ME and MEET protocols，the proposed protocol can better bal⁃ance the nodes’energy consumption，enhance the network stability and improve the quality of network service.

Key words：wireless sensor network；balancing energy-consumption；region-divided algorithm；selectional mecha⁃nism of cluster heads

doi：EEACC：6150P；723010.3969/j.issn.1004-1699.2016.01.015

收稿日期：2015-07-22修改日期：2015-10-15

中图分类号：V241.5

文献标识码：A

文章编号：1004-1699（2016）01-0075-05

项目来源：内蒙古自然科学基金面上项目（2012MS0924）;内蒙古自治区重大基础研究开放课题项目（内蒙古工业大学内蒙古自治区机电控制重点实验室）