光纤陀螺随机误差特性ThêoH辨识

徐东升，陆　明，贾长治，康海英（1.解放军理工大学野战工程学院，南京10007；.军械工程学院火炮工程系，石家庄050003）



光纤陀螺随机误差特性ThêoH辨识

徐东升1，2，陆明1*，贾长治2，康海英2
（1.解放军理工大学野战工程学院，南京210007；2.军械工程学院火炮工程系，石家庄050003）

摘要：随机误差特性分析是光纤陀螺进入工程应用阶段的关键技术。针对Allan方差、总方差、Thêo1 （Theoretical variance #1）等分析方法的不足，以Thêo1为基础，通过偏差消除获得ThêoBR（Bias-removed ver⁃sion of Thêo1），并将其与Allan方差合成，得到光纤陀螺随机误差特性分析的ThêoH（Hybrid-ThêoBR）法。通过计算重叠Allan方差、总方差、Thêo1以及ThêoH的等效自由度，结合仿真和实测信号的随机误差特性分析实验，证明ThêoH法不仅提高了Allan方差估计的置信度，且解决了Thêo1估计有偏的问题，表明了该方法是目前能够有效辨识光纤陀螺随机误差特性的最佳方法。

关键词：光纤陀螺；随机误差；ThêoH；无偏估计

光纤陀螺具有体积小、功耗低、无机械运动部件等优点，在导航控制等多领域具有广泛的应用前景，因此受到世界各国的高度重视。目前，中低精度的光纤陀螺已经获得了广泛应用，而高精度光纤陀螺的推广还存在一些关键技术亟待突破，其中最突出的问题是存在很多难以解决的确定性误差和随机误差。为了减小光纤陀螺的误差提高精度，需要建立系统误差模型补偿确定性误差，并对光纤陀螺随机特性进行评价，辨识出影响其精度的主要随机误差项，进而采取适当措施控制其噪声水平［1］。

根据IEEE标准关于光纤陀螺随机误差的定义，光纤陀螺随机误差主要包括量化噪声、角度随机游走、零偏不稳定性、速率随机游走以及速率斜坡等能量谱密度相互独立的5类噪声项，其经典的辨识方法包括自回归滑动模型（ARMA）、功率谱密度法以及Allan方差法［2］。其中，ARMA在噪声较大时模型精度会受到一定的影响；功率谱密度法分析时，不同噪声项的功率谱密度对数曲线可能相似度较高，从而难以区分［3］；而Allan方差法是在时域分析频域稳定性的方法，应用于光纤陀螺随机误差辨识效果较好且实用性很强，因此被IEEE推荐为进行光纤陀螺随机误差特性辨识的方法。Allan方差法也存在一定的不足，其主要问题是：当平滑因子较大时，该方法辨识结果置信度较差。一般要求在进行Allan方差计算时，其平滑时间应小于总采样时间的20%。当采样数据时间较短时，不宜采用Allan方差进行辨识。为此，在Allan方差的基础上发展了总方差以及Thêo1等辨识方法。总方差和Thêo1法大幅提高了估计值的置信度，但总方差法映射延伸采样数据的同时也造成了数据的不连续性，致使其估计是有偏的，且延伸的数据是人为给定的，有时不能真实反映被测系统的特性，因此存在不可避免的缺陷；而Thêo1将平滑时间乘以3/4进行采样，其估计也是有偏的［4-5］。针对这一情况，本文引入ThêoBR消除Thêo1与Allan方差之间的偏差，并将其与Allan方差合成得到ThêoH，利用该方法分析光纤陀螺随机误差特性既能保持较高的估计值置信度，且为无偏估计，因此将具有良好的辨识效果。

1　Allan方差、总方差及Thêo1

1.1Allan方差

假设某一光纤陀螺输出的角速率采样信号数据序列为{yi，i=1，2，…，N}，采样间隔时间为t0，将该数据序列划分为k组，每组m个采样点，即m=N/k，定义

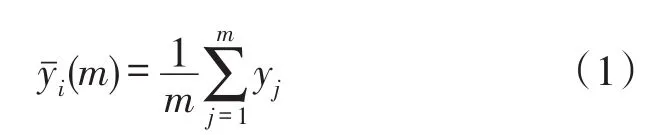
则Allan方差为［6］：

Allan方差与光纤陀螺随机误差的功率谱密度Sy（f）之间的存在确定的转换关系［7］

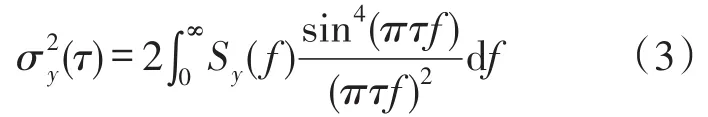
因此，Allan方差估计是无偏的，在进行光纤陀螺随机特性分析时，通过计算其Allan方差，绘制Allan方差和相关时间（σ（t）~t）的双对数曲线图，从而辨识出光纤陀螺的不同随机误差项，进一步对双对数该曲线进行拟合，可以求取各误差项的系数。Allan方差的估计值可以看作是一组决定于划分组数k的随机变量，因此随着相关时间τ增大，划分的组数减少，Allan方差估计值的置信度降低，其1σ的百分比误差E可以表述为

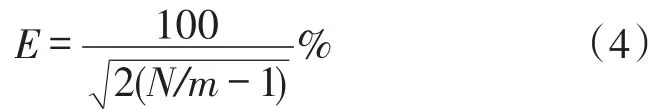
式中，N为数据长度，m为划分的数据组数。

为了减小Allan方差估计的误差，一般在进行Allan方差分析时，采用重叠采样进行估计，重叠采样Allan方差定义为［7-8］：

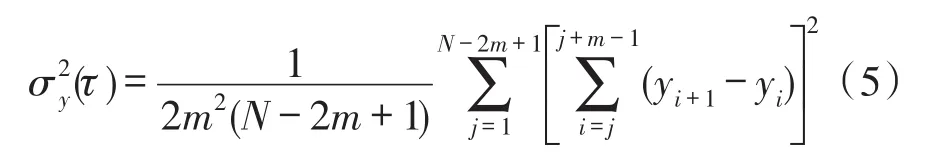
式中，N、m等参数代表的物理意义与式（1）和式（2）中相同。

重叠采样Allan方差通过最大限度形成所有平滑时间为mt0的子序列，充分利用已有采样数据进行分析，提高了估计值的置信度，因此在进行Allan方差分析时，一般采用重叠Allan方差进行估计。

1.2总方差

对应Allan方差中对原始数据序列的假设，按如下方式进行扩展，产生延伸序列{y#i，i=1，2，…，N}，其中

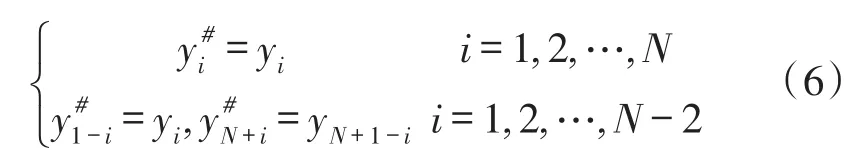
对于延伸后的序列，总方差定义为［9］：

对比Allan方差和总方差可以看出，通过映射将原始数据长度由N延伸到3N-2，总方差估计的最大平滑因子可以达到N，相对于Allan方差估计的N/2扩展了一半的数据长度，因此在长相关时间下能够提高估计值的置信度。但是，数据延伸扩展的同时也造成其本身的不连续性，致使总方差估计值相对于Allan方差是有偏的，该偏差计算表达式为［10-11］

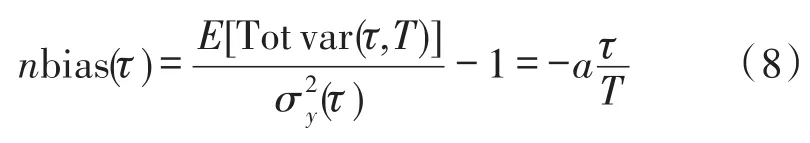
式中，t表示平滑时间，T为总采样时间，a为偏差因子，其取值与噪声类型有关。当噪声类型为零偏不稳定性、速率随机游走以及速率斜坡时，a=0；当噪声类型为量化噪声时，a=0.75；当噪声类型为角度随机游走时，a=0.48。因此，对于量化噪声和角度随机游走，总方差相对于Allan方差是有偏估计，其偏差随着平滑时间的增大而增大。当平滑时间t=T/2，量化噪声估计的偏差将达到37.5%，角度随机游走估计的偏差将达到24%。另外，总方差法中两端的延伸数据是人为设定的，这些数据有时并不能如实体现被测系统的真实性能，因此总方差法具有不可避免的缺陷。

1.3Thêo1方差

Thêo1是由美国国家标准局（NIST）提出的一种新的描述频率稳定性的方差分析方法，其计算表达式为［12-13］：

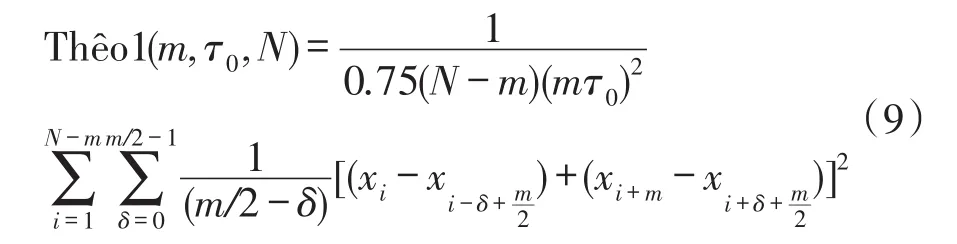
式中，{xi，i=1，2，…，N}表示时偏采样数据长度，t0为数据采样时间间隔，Nt0为总测量时间长度，m= 10，…，N-1且m为偶数。

Thêo1方差的主要特点是采用了新的采样数据方法，其计算的相关时间的步幅ts=0.75mt0，而m最大可取到N-1，二次采样的相关时间可以达到0.75 （N-1）t0，即可以达到总测量时间的75%，而Allan方差二次采样的最大相关时间为Nt0/2，只能达到总测量时间的一半。因此，Thêo1方差在长相关时间测试中具有很大的优势，是目前所有估计长期频率稳定性的方差算子中置信度最高的一种［1］。

虽然Thêo1相对于Allan方差估计值置信度有很大的提高，但是Thêo1方差相对于Allan方差估计是有偏的，对于光纤陀螺的5项主要噪声，其偏差可以由表1近似表示［5］。

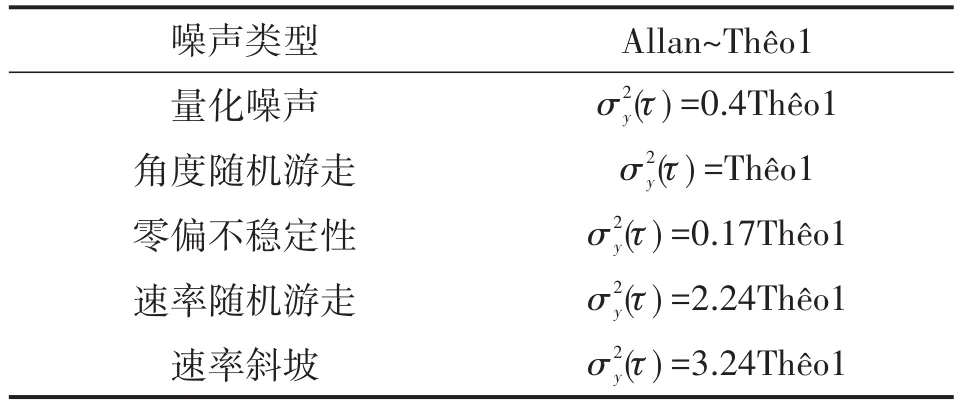
表1　Thêo1相对Allan方差的偏差

2　ThêoH

采用表1中的系数消除Thêo1相对Allan方差的偏差具有计算简便的优势，但是利用该经验公式计算必须首先假设噪声类型已知，且当平滑因子m>N/2（N为采样数据点数）时，Allan方差不存在，此时其相对偏差无法估计。为此，本文引入ThêoBR去除Thêo1的相对偏差，其计算表达式为［14］：

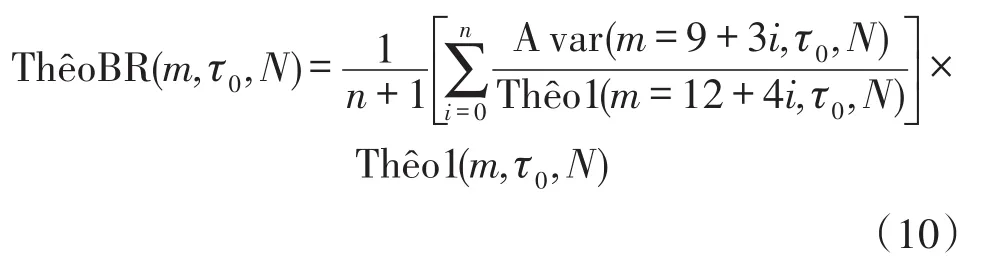
式中，Avar（）表示重叠Allan方差，Thêo1（）表示Thêo1方差，n=‖0.1N/3-3‖，‖‖表示数值向下取整。

ThêoBR去除了Thêo1方差与Allan方差之间的偏差，可以表述为Allan方差在最大可能平滑因子上的无偏估计。因此，对Allan方差和ThêoBR进行合成，可以得到一种新的方差，称为ThêoH，其计算表达式为［15-16］：

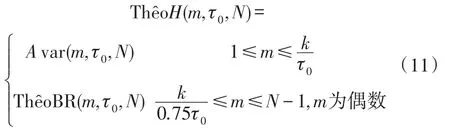
其中k表示τ<0.1Nt0时的最大值。

ThêoH是在Thêo1的基础上去除偏差并与Allan方差进行合成的结果，其最大平滑因子可以达到0.75N，相对Allan方差估计有很大提高。ThêoH利用ThêoBR去除偏差，而且能够适应多种噪声混合时频率稳定性的估计，因此在光纤陀螺随机误差特性辨识，尤其是在大平滑因子条件下具有很大的优势。

3　估计置信度对比分析

利用Allan方差、总方差、Thêo1以及ThêoH辨识光纤陀螺的随机误差特性，其估计值可以视为一组随机变量，因此在计算时应当给出相应的估计置信度，以判定该估计是否有效。估计值的置信度决定于方差类型、数据长度、平滑因子以及噪声类型、置信因子等多个条件。对于Allan方差，估计置信度可以采用公式（4）进行计算；对于重叠Allan方差、总方差、Thêo1以及ThêoH，最常用的方法是按照指定的置信因子基于χ2统计量进行计算。

根据基于χ2统计量计算置信区间的方法，定义采样方差分布函数为：

式中，edf为等效自由度，其大小由方差类型以及数据长度、噪声类型等确定，S2为采样方差，σ2为真实方差，通常以多组采样方差的平均值代替。根据公式（12），当指定置信因子p后，可以确定各方差估计置信度决定于等效自由度，等效自由度越大，估计的置信度就越高。因此，比较重叠Allan方差、总方差以及Thêo1方差估计的置信度实质为比较各方差的等效自由度。等效自由度计算的表达式为：

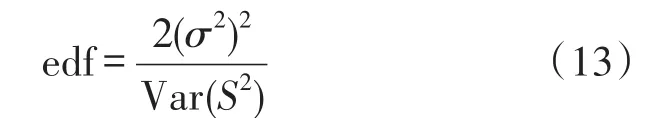
式中，Var（S2）表示S2的方差。

实际计算中，等效自由度常常针对不同的噪声类型采用经验公式进行计算。对于功率谱密度相互独立的5类噪声，其重叠Allan方差等效自由度计算公式分别为［17］：

式中，N为采样数据点个数，m为平滑因子。

总方差等效自由度可以依据重叠Allan方差以及经验公式计算。当噪声为速率随机游走噪声和速率斜坡时，总方差的等效自由度比重叠Allan方差等效自由度多两个；当噪声为量化噪声、角度随机游走和零偏不稳性时，总方差等效自由度的计算依据以下经验公式［18-19］：

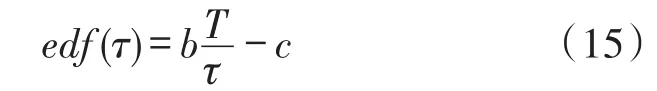
b和c的取值如表2所示。

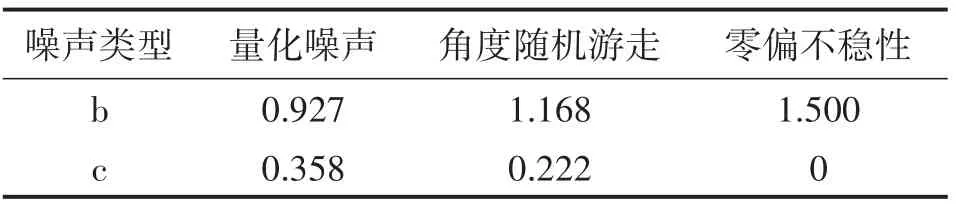
表2　不同噪声类型下b和c的取值

应当注意的是上述公式是基于函数连续推导的，在进行计算时，对于零偏不稳定性要求t满足τ≥8τ0，对于角度随机游走噪声要求t满足t≥3τ0。

利用Thêo1方差进行估计，5类噪声项等效自由度计算公式为［20］：

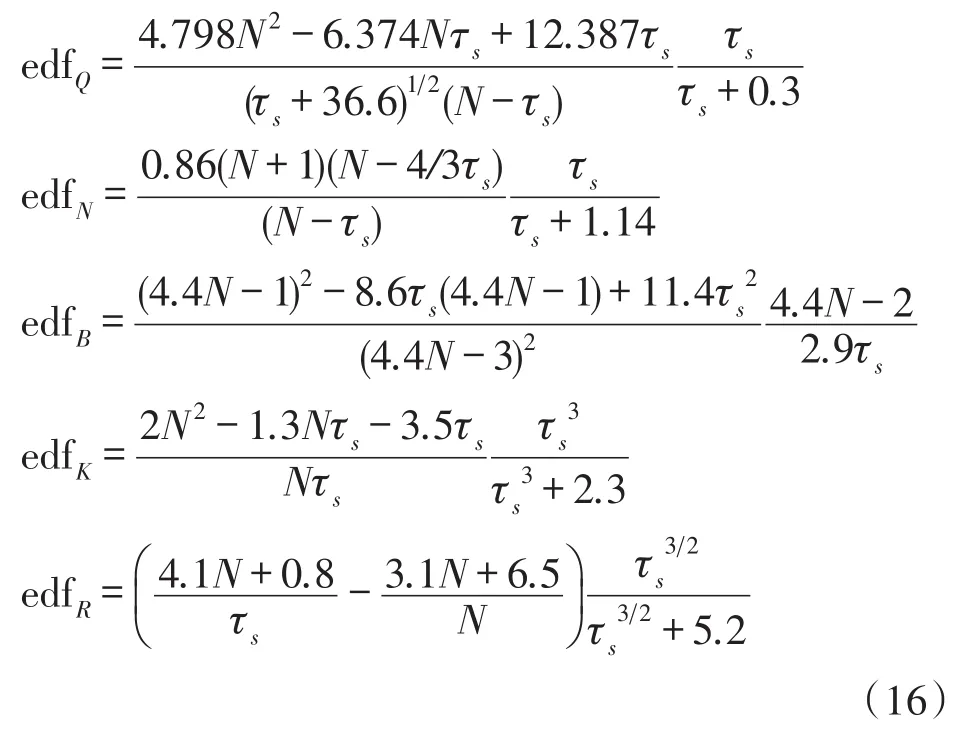
式中，N为采样点数据个数，τts为采样时间，且ts= 0.75mt0，t0≤T/10。

与Thêo1方差相比较，ThêoH估计的等效自由度为［21］：

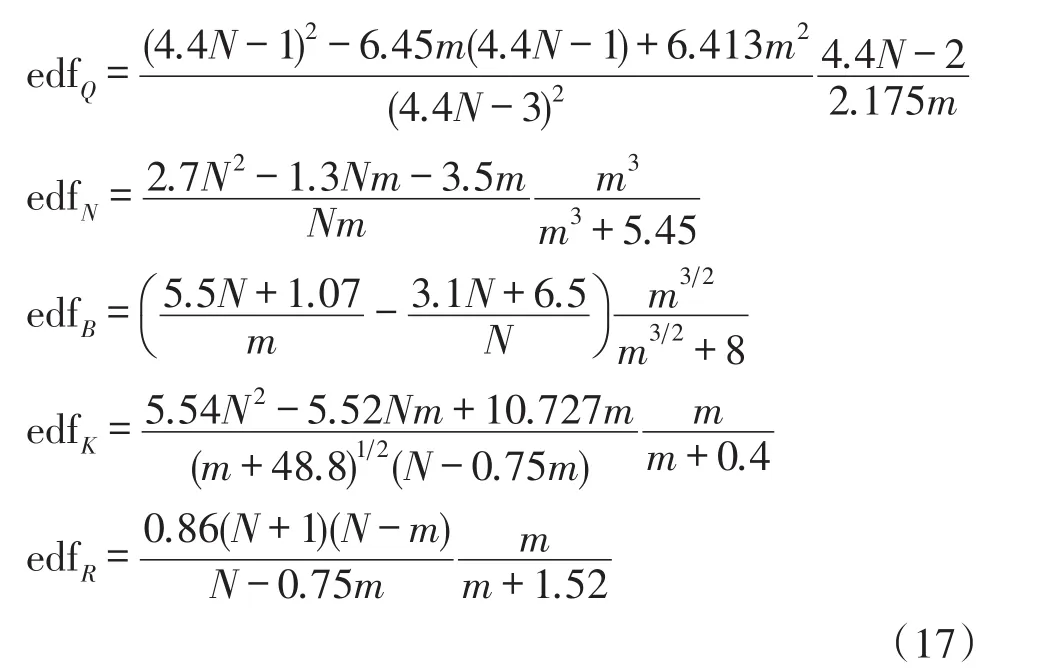
式中，N为采样数据点数，m为平滑因子。

图1~图5绘制了5类噪声项的重叠Allan方差、总方差、Thêo1以及ThêoH的等效自由度。图中采样数据点数N设定为1000，采样时间间隔t0设定为0.01 s。

图1~图5表明，对于5类功率谱密度相互独立的噪声项，总方差、Thêo1以及ThêoH的等效自由度均大于重叠Allan方差；而随着平滑因子的增大，Thêo1的等效自由度相对于总方差及ThêoH都有明显的优势；另外，对于量化噪声、角度随机游走以及零偏不稳定性，总方差的等效自由度大于ThêoH方差，对于速率随机游走和速率斜坡，ThêoH的等效自由度大于总方差。因此，对于上述4种方差估计，总方差、Thêo1以及ThêoH相对于重叠Allan方差具有更高的估计置信度，其中Thêo1估计的置信度最高，总方差和Thêo1方差则针对不同的噪声类型，在估计置信度上各有优势。

图1　量化噪声等效自由度

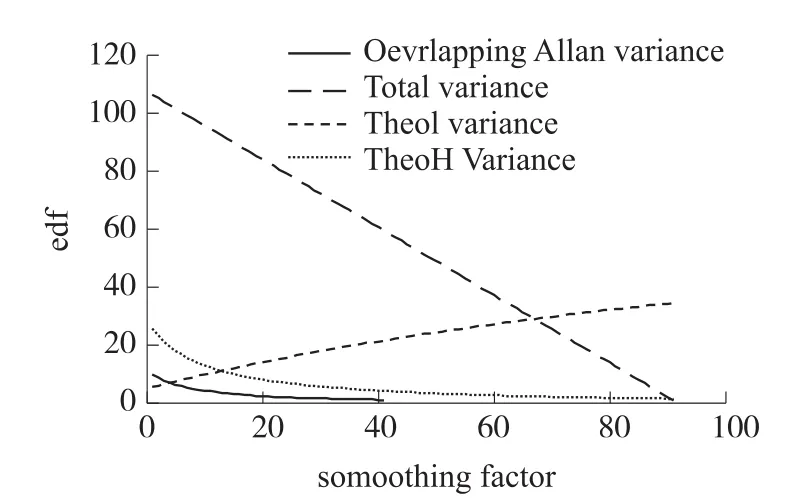
图2　角度随机游走等效自由度

图3　零偏不稳定性等效自由度

图4　速率随机游走等效自由度

图5　速率斜坡等效自由度

4　实验及结果讨论

在Allan方差、总方差以及Thêo1、ThêoH的估计值与平滑时间构成的双对数图中，对应的曲线斜率表征了光纤陀螺的不同噪声类型及其参数。以下本文将设计仿真实验和实测信号噪声特性分析实验，验证Allan方差、总方差以及Thêo1、ThêoH能够实现光纤陀螺噪声特性的辨识，并进一步对比各方差在光纤陀螺噪声特性分析中的优越性。

4.1仿真实验

光纤陀螺5类噪声项中的角度随机游走主要来源于光源的光子噪声、相对强度噪声以及探测器的散粒噪声、热噪声等，这类噪声主要为白噪声［19］；而对白噪声进行数值积分，则可以表征光纤陀螺的速率随机游走。如图6和图7所示，分别用采样点数N=1000、采样时间t=0.01s、均值为0、方差为1的白噪声及其数值积分表征角度随机游走和速率随机游走。

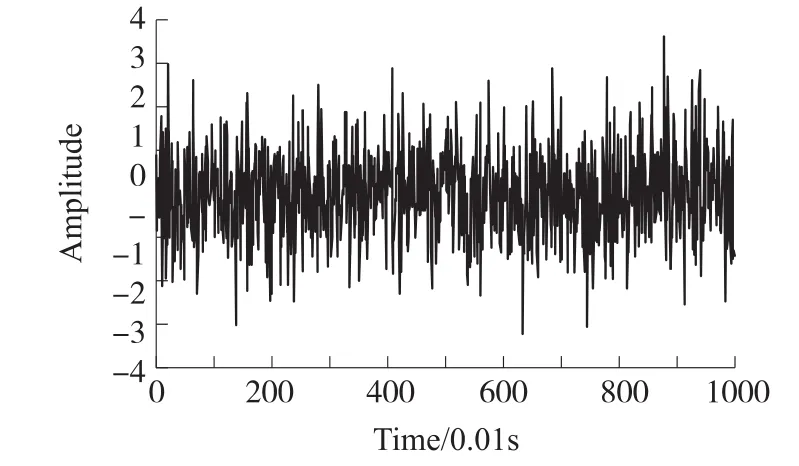
图6　角度随机游走

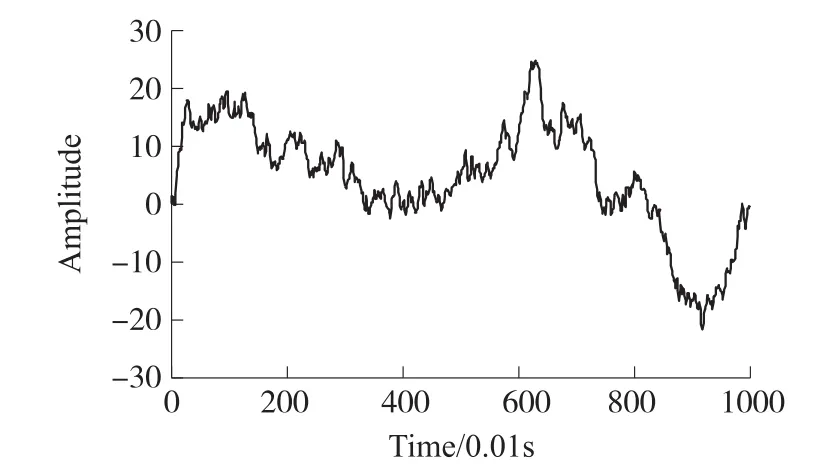
图7　速率随机游走

对白噪声及其积分表征的角速度随机游走及速率随机游走，分别计算其Allan方差、总方差以及Thêo1、ThêoH，结果如图8和图9所示。

图8反映出对于角度随机游走，Allan方差、总方差以及Thêo1、ThêoH能够实现随机误差特性辨识，但是当相关时间较长时，Allan方差估计由于置信度较低会出现一定的波动，而总方差、Thêo1以及ThêoH估计值对数曲线相对平滑，证明其置信度较高；图9针对速率随机游走进一步印证了图8中的结论，并反映出相对于Allan方差估计，Thêo1对速率随机游走的估计是有偏的。

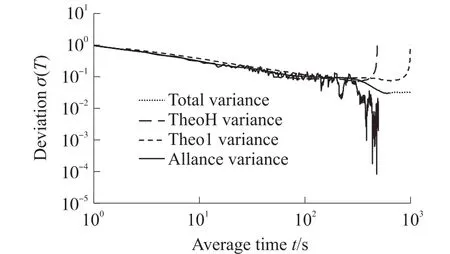
图8　角度随机游走仿真分析结果

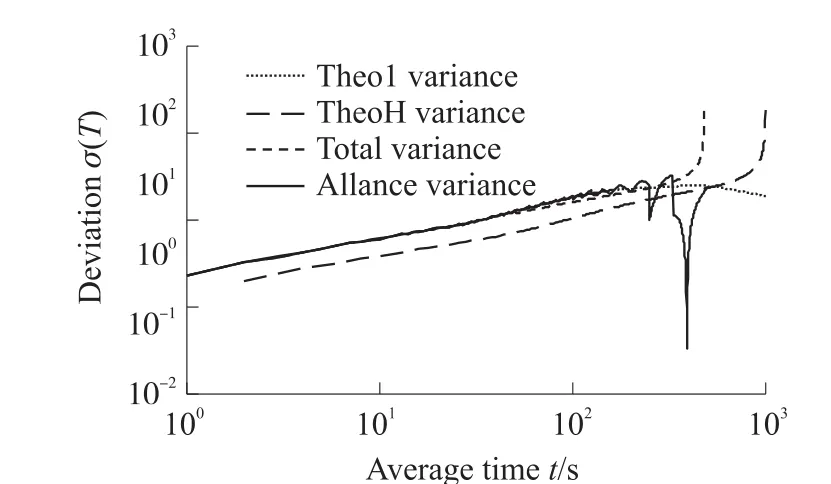
图9　速率随机游走仿真分析结果

4.2实测信号随机误差特性分析实验

仿真实验证明总方差以及Thêo1、ThêoH相对Allan方差估计的置信度有很大的提高，且Thêo1估计是有偏的，但是，对于前述总方差估计的有偏性并未得到体现。为此，本文将通过分析光纤陀螺实测信号的随机误差特性对比各方差估计的优劣。

如图10所示是某型光纤陀螺实测信号，总测试时间为3000s，采样间隔为0.3 s，对该实测信号进行Allan方差、总方差、Thêo1以及ThêoH计算，其结果如图11所示。

图11的计算结果表明，利用总方差、Thêo1和ThêoH辨识该型光纤陀螺的随机误差特性，其估计值置信度相对Allan方差有较大的提高，但是总方差和Thêo1估计是有偏的，且相关时间较短时Thêo1估计偏差大于总方差偏差，相关时间较长时总方差估计偏差大于Thêo1偏差，而ThêoH估计则是无偏的，因此ThêoH更适用于光纤陀螺随机误差特性的辨识。

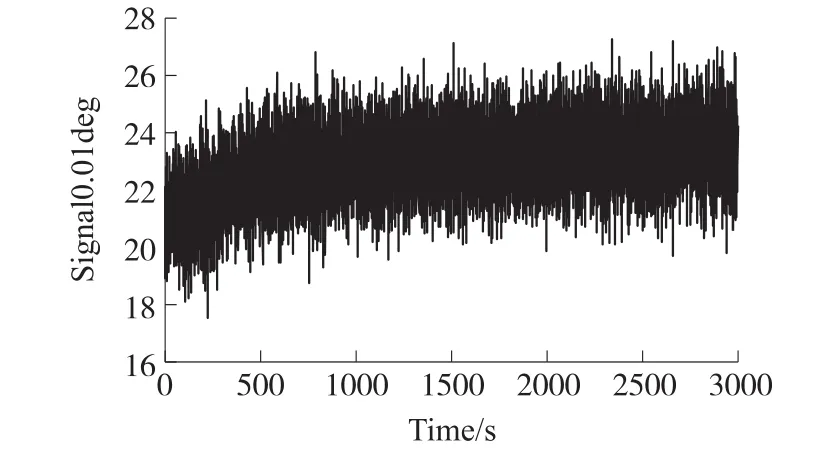
图10　某型光纤陀螺实测信号

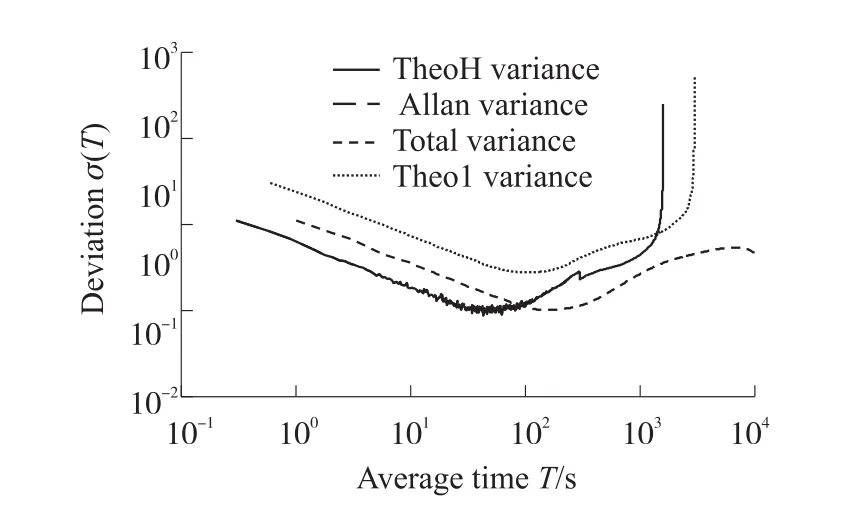
图11　实测信号误差特性各方差分析结果

依据辨识结果，利用最小二乘法拟合ThêoH曲线，得到的光纤陀螺各项噪声系数，如表3所示。表3中各噪声类型及其噪声系数表明速率斜坡、角度随机游走以及量化噪声为该组实测信号的主要噪声项，而根据前述分析，采用Thêo1估计速率斜坡及量化噪声将引起的较大偏差，采用总方差估计角度随机游走及量化噪声将引起随相关时间增长而增大的偏差，这就进一步验证了实测信号随机误差特性辨识结果与前述理论分析是吻合的。

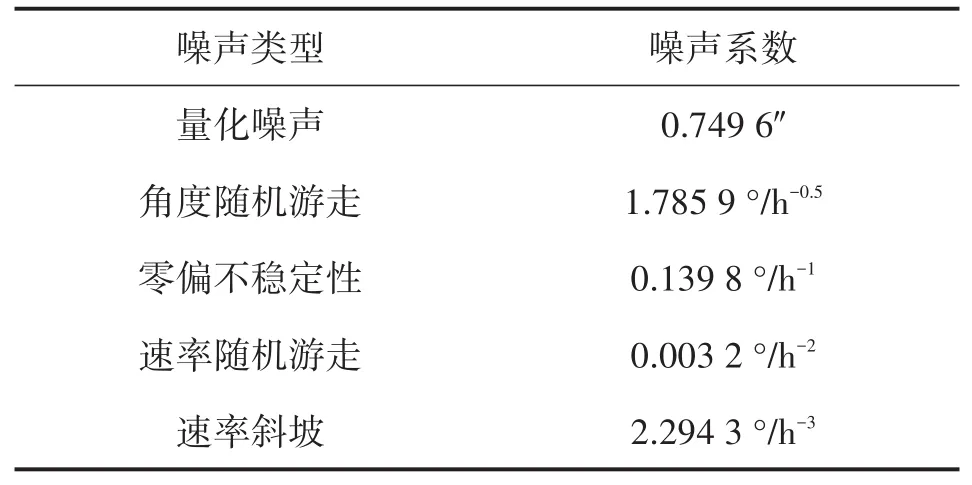
表3　光纤陀螺各项噪声ThêoH辨识结果

5　结论

随机误差特性分析是光纤陀螺进入工程应用阶段的关键技术。本文介绍了光纤陀螺随机误差特性辨识的Allan方差、总方差和Thêo1方法，并针对其不足，提出采用ThêoH分析光纤陀螺的随机误差特性。通过对比重叠Allan方差、总方差、Thêo1以及ThêoH的估计置信度，并结合仿真和实测信号随机特性分析实验，证明ThêoH作为一种具有较高估计置信度的无偏估计方差，有效解决了Allan方差、总方差以及Thêo1估计存在的问题，是目前能够实现光纤陀螺随机误差特性辨识的最佳方法。

参考文献：

［1］韩军良.光纤陀螺的误差分析、建模及滤波研究［D］.哈尔滨：哈尔滨工业大学博士学位论文，2008.

［2］Skaloud J，Bruton A M，Schwarz K P. Detection and Filtering of Short-Term（1/f Exp Gamma）Noise in Inertial Sensors［J］. Navi⁃gation，1999，46（2）：97-107.

［3］刘付强.船用卫星天线微型姿态测量系统关键技术研究［D］.哈尔滨：哈尔滨工程大学，2008.

［4］Li J T，Fang J C. Not Fully Overlapping Allan Variance and Total Variance for Inertial Sensor Stochastic Error Analysis［C］// IEEE Transactions on Instrumentation and Measurement，2013，62 （10）：2659-2672.

［5］程旭维，汤霞清，黄湘远.基于＃1理论方差的光学陀螺长期随机误差分析［J］.中国激光，2014，41（10）：1005003.

［6］姬伟，李奇.光纤陀螺信号误差分析与滤波算法的研究［J］.传感技术学报，2007，20（4）：847-852．

［7］方琳，申冲，陈熙源.基于小波多尺度变换的光纤陀螺振动误差分析与补偿［J］.传感技术学报，2012，25（7）：902-906.

［8］李晓莹，胡敏，张鹏，等.交叠式Allan方差在微机械陀螺随机误差辨识中的应用［J］.西北工业大学学报，2007，25（2）：225-229.

［9］Howe D A. Total Variance Explained［C］//Jiont Meeting EFTEIEEE IFCS，1999：1093-1099.

［10］Howe D A. The Total Deviation Approach to Long-Term Charac⁃terization of Frequency Stability［C］//IEEE Transactions on Ultra⁃sonics Ferroeletrics and Frequency Control，2000，47（5）：1102-1110.

［11］Greenhall C A，Howe D A，Percival D B. Total Variance，an Esti⁃mator of Long Term Frequency Stability［C］//IEEE Transactions on Ultrasonics，Ferroelectrics，and Frequency Control，1999，46 （5）：1183-1191.

［12］Howe D A，Tasset T N. Theo1：Characterization of Very Long-Term Frequency Stability. Proceedings of the 18thEuropean Fre⁃quency and Time Forum［C］//2004，4：581-587.

［13］Tasset T N，Howe D A，Percival D B. Theo1 Confidence Intervals ［C］//IEEE International Ultrasonics，Ferroelectrics and Frequen⁃cy Control Joint 50th Anniversary Conference，2004：725-728.

［14］Howe D A，Taylor M G，Tassett G. TheoH Bias-Removal Method［］. National Institute of Standards and Technology 325 Broad⁃way，Boulder，CO 80305 USA，2006：788-792.

［15］Jennifer A M，Howe D A. TheoH and Allan Deviation as Power-Law Noise Estimators［C］//IEEE Transactions on Ultrasonics，Ferroelectrics，and Frequency Control，2007，54（2）：448-452.

［16］焦月，张升康.频率稳定度测量方法的对比分析［J］.宇航计测技术，2013，33（1）：35-37.

［17］Howe D A，Allan D W，Barnes J A. Properties of Signal Sources and Measurement Methods［C］//Proc 35th Ann Freq Control Sym⁃posium，USAERADCOM，Ft Monmouth，NJ，1981，A：1-47.

［18］Burch B D. Generalized Confidence Intervals for Proportions of Total Variance in Mixed Linear Models［J］. Journal of Statistical Planning and Inference，2007（137）：2394-2404.

［19］郭海荣，郭树人，焦文海.原子钟时域频率稳定度分析中等效自由度的计算与分析［J］.天文学进展，2007，25（4）：375-383.

［20］郭海荣.导航卫星原子钟时频特性分析理论与方法研究［D］.郑州：解放军信息工程大学，2006.

［21］Howe D A. TheoH：a Hybrid，High Confidence Statistic that Im⁃proves on the Allan Deviation［J］. Metrologia，2006，43：S322-S331.

徐东升（1988-），男，安徽黄山人，博士研究生，研究方向为武器系统运用工程，xds19881127@163.com；

陆明（1958-），男，江苏南京人，博士生导师，研究方向为军用精确爆破，305497576@qq.com.

Mobile Robot Target Recognition Based on Dynamic Template Matching*

PENG Yuqing*，LI Mu，GAO Qingqing，ZHANG Yuanyuan
（Department of Computer Science and Technology，Hebei University of Technology，Tianjin 300401，China）

Abstract：A target recognition strategy under unknown environments for mobile robot was presented with the combi⁃nation of vision salience and the target recognition method based on dynamic template matching. Specifically，a mo⁃bile robot vision system based on distributed control was designed for improving the efficiency of video processing. Secondly，the saliency measure based on background priors was used for image preprocessing and excluded the background regions which were less important. Finally，the recognition accuracy of the target was improved accord⁃ing to the dynamic template matching to images which had been processed. The experimental results show that the method can meet the requirements of real-time and veracity in the process of mobile robot’s target recognition，the method show good effectiveness.

Key words：mobile robot；target recognition；template matching；vision salience；distributed control

doi：EEACC：6135；722010.3969/j.issn.1004-1699.2016.01.011

收稿日期：2015-07-14修改日期：2015-10-21

中图分类号：TN256

文献标识码：A

文章编号：1004-1699（2016）01-0051-07