基于载波相位的GPS周跳恢复方法研究

吕振扬，刘伯鸿，伏玉明

（兰州交通大学自动化与电气工程学院，甘肃兰州730070）



基于载波相位的GPS周跳恢复方法研究

吕振扬，刘伯鸿，伏玉明

（兰州交通大学自动化与电气工程学院，甘肃兰州730070）

摘 要：在GPS定位中，周跳的探测和修复是获得高精度定位结果的前提。针对载波相位周跳数据的探测和修复这一问题已经提出了很多方法，但都有各自的不足之处。文中针对恶劣环境下的载波相位定位问题，通过使用多个历元的数据构建方程，提出一种新的整周模糊度定义方法，并预期能够在仅有3颗可用卫星且周跳发生时实现快速、准确的定位。

关键词：GPS；载波相位；周跳；整周模糊度

随着GPS（全球定位系统）被越来越广泛地用于获取用户的位置信息，例如汽车导航，以及移动电话等，在人类生活中成为了重要的组成部分。因此定位精度的逐步提高是非常必要的。载波相位定位这种精确定位的方法也受到人们越来越多的关注［1－4］。载波相位定位时，则需要计算接收机和卫星之间的波数，并且只要保持接收GPS信号则该值不变。目前城市的网络RTK全部采用载波相位定位，但在复杂的城市环境中，信号容易受到障碍物的拦截，导致该值发生变化，这就是所谓的周跳。

通过GPS载波相位实现高精度定位最主要的问题在于准确地获得整周模糊度。整周模糊度的参数大多采用整数最小二乘估计的方法求解。近几年出现了许多相关的搜索算法，主要有：最小二乘模糊搜索技术［5］、整型模糊度求解法［6］和快速模糊求解方法（FARA）［7］等。本文提出一种在周跳发生时重新定义整周模糊度的方法，并预期能够借此实现在复杂城市环境中的精确定位［8］。

1　载波相位差分定位原理

为了定位接收机，需要计算各GPS卫星和接收机之间的距离。已知接收机接收到的各GPS卫星的三维坐标（xi，yi，zi），可以将接收机和各GPS卫星之间的距离表示为［9］

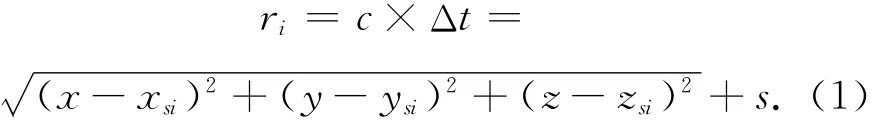
式中：ri为接收机和每个GPS卫星之间的距离，c为光速，Δt为波的传输时间，（x，y，z）为接收机坐标，s为接收机钟差引起的误差。伪距包含的误差因素如下：

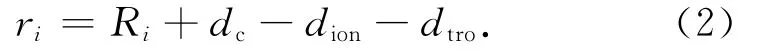
式中：dc为卫星钟差引起的误差，dion为电离层延迟误差，dtro为对流层延迟误差。Ri表示伪距无修正。为了获得精确的误差范围，消除卫星钟差和接收机钟差的影响，载波相位测量通常使用二次差分方法。

参考接收机R和用户接收机U，通过载波相位定位接收机R，U和卫星K，L两两之间的距离分别为rkr，rku，rlr，rlu。双差Φklru可通过式（3）求得，如图1所示。

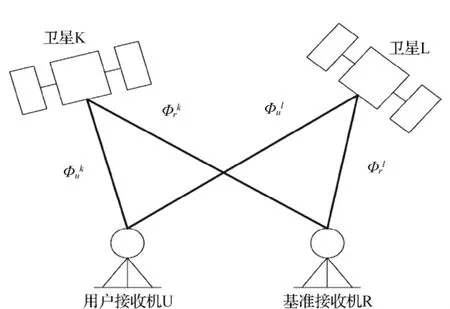
图1　双差原则

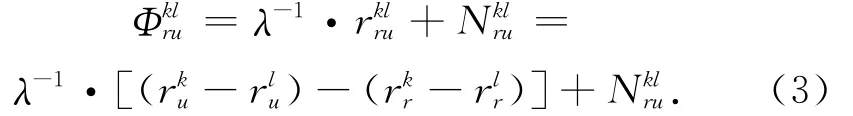
式中，Nklru为整周模糊度，为未知整数，且收敛很慢［10］。Nklru一旦被定义，只要接收机持续接收GPS信号，则该值不变。

2　差分GPS数学模型

如果可以观察到足够的卫星，刚好可以得到用户的位置（xu，yu，zu）和模糊值Nklru。假定N已经被定义，可以设想利用很少的可观察卫星进行定位。具体方法如下：

2．1 可观察到4颗卫星

在时间T可见卫星有4颗，假定卫星1是基本星。如果每颗卫星的模糊值已定义，并求得伪距，通过载波相位求得双差，此时有以下3个方程式［11］：

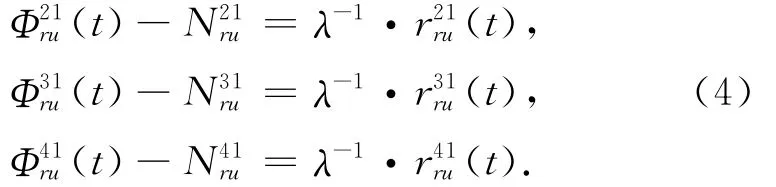
上述方程组中未知值的数量有3个（xu，yu，zu），理论上可以解出未知数。

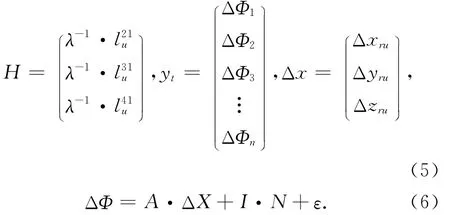
位置X的值由修正值ΔX更新。

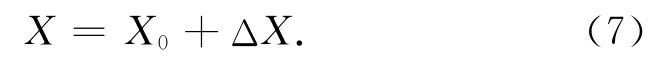
式中，X0是默认位置，通过伪距进行定位计算。

2．2 可观察到3颗卫星

如果4颗卫星中有1颗无法被观察到，将不能继续精确定位，因为此刻有3个未知数的值（xu，yu，zu），但只有两个方程式。

假定Z轴方向的分量固定不变，此刻未知数（xu，yu）可由式（8）求解［12］。

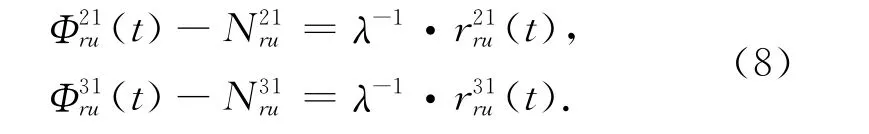
理论上可以通过减少未知值的个数从而求得位置参数。

2．3 发生周跳后的过程

当2．2中的可见星无法观察到时将产生周跳现象，此时需重新定义卫星的整周模糊度。根据该方法，通过在2．2中求得的位置参数计算该值。

假设有4颗可见星，并设定卫星1是基本星，能够求得双差和3个方程

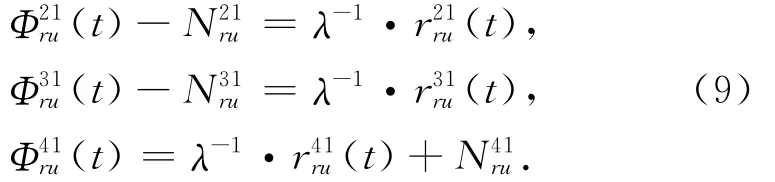
但此时有4个未知值而仅有3个方程，所以理论上该方法无法实现。

因此，通常使用两个历元的数据来进行求解，即历元t和t＋1，如式（10）所示。

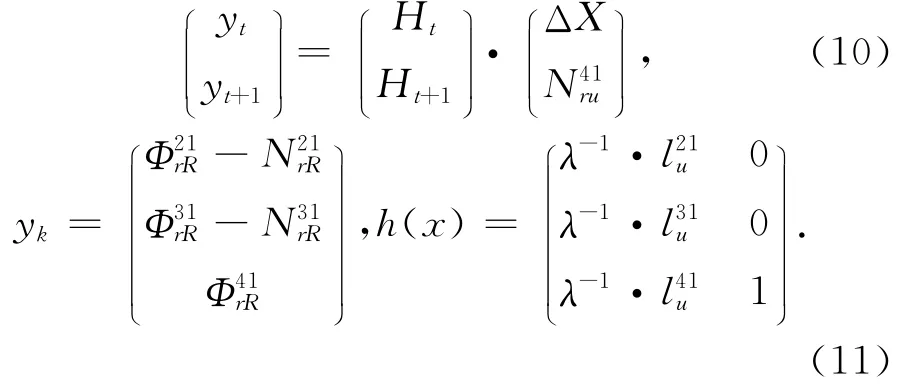
通过上述计算之后，求得参数并带入式（5）～（7）计算。

2．4 Z轴方向的分量发生变化

如果接收机的位置发生改变，即Z轴方向的分量发生变化，此时需预测接收机和不可见的卫星之间的距离。

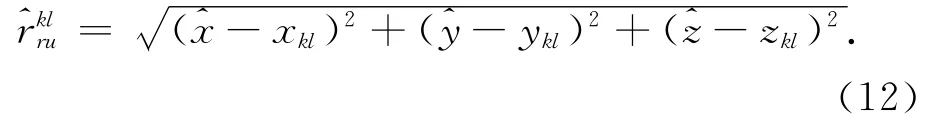
3　仿真实验

设置GPS接收机的高程截止角为5°，数据采样间隔为1s。对照试验使用数据为接收机热启动后300s内接收的数据。由于在市区中接收机的可用卫星数目会受周围环境影响而不断变化，而在某些时刻接收机的可见卫星仅有3颗。

图2显示的是当接收机的可用卫星的数目从4颗变为3颗时分别采用两种方法所获得的定位结果（实验过程中每秒采集一次数据）。三角形表示接收机正常工作时的定位结果，而圆形表示利用上述方法进行定位的结果。原点（0，0）是接收机的真实位置。

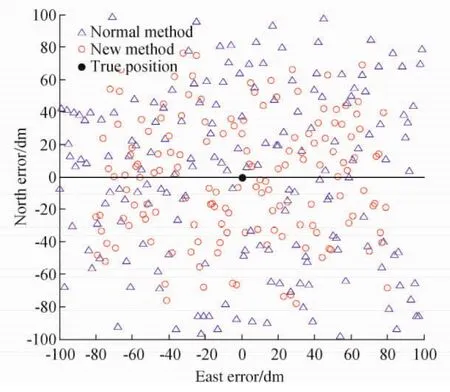
图2　接收机定点定位结果

图2显示，通过载波相位进行定位，接收机的定位精度得到较大的改善。实验证明，新的方法提高了定位的精度，但是这一结果低于对载波相位的预期。究其原因在于仅使用两个历元的数据来计算位置和整周模糊值，浮点的精度并不能完全收敛。

仅有3颗卫星时，如果发生周跳接收机将无法准确定位，此时用本文提出的方法尝试进行定位。图3显示接收机正常定位时的定位结果，其在垂直方向的最大误差达到100dm，平均误差为59dm；图4显示利用本文方法定位时接收机的定位结果，其在垂直方向的最大误差达到82dm，平均误差为41dm。实验证明，新的定位方法获得的结果相比原有方法，定位的精度得到了较大的提高。因此，该方法可以有效地修复定位误差。

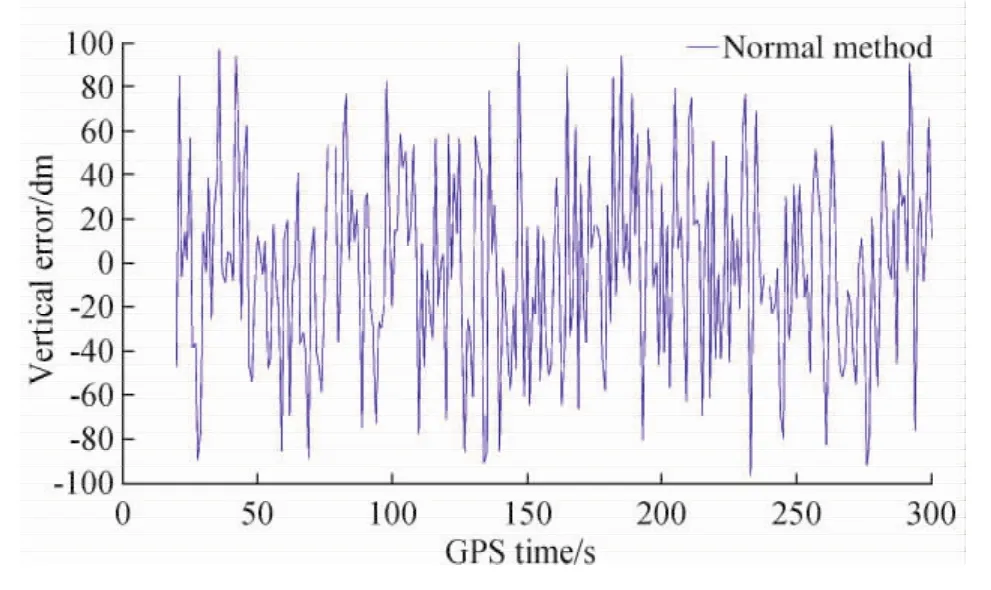
图3　接收机正常工作定位误差

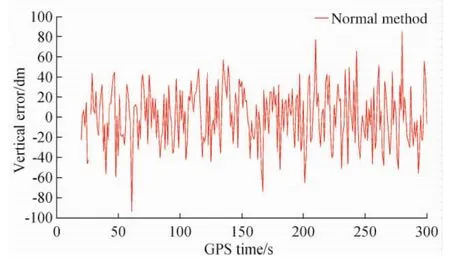
图4　改进方法定位误差

4　结 论

快速、准确地解算出整周模糊度是通过GPS载波相位实现高精度定位的前提。本文提出了一种在复杂城市环境中，当可见星数不足4颗且发生周跳时，重新定义整周模糊度的方法，提高了GPS接收机定位的速度和准确性。

实验证明，本文针对复杂城市环境中GPS定位精度较低这一问题所提出的方法有很好的效果。通过该方法，动态目标在该复杂环境中的定位精度也获得了一定程度的提高，但效果并不明显。如何进一步提高复杂城市环境中恶劣条件下动态目标的定位精度，是接下来需要解决的关键问题。

参考文献：

［1］ 温旭．基于小波变换的GPS整周跳变的探测及修复［D］．赣州：江西理工大学，2009．

［2］ 张晖，陆敏燕．单频精密单点定位周跳探测方法研究［J］．测绘与空间地理信息，2015，38（1）：132－134．

［3］ 王金龙，兰孝奇，高奋生．多项式拟合法和电离层残差法联合探测与修复周跳［J］．测绘工程，2013，22（1）：25－27．

［4］ 任小伟．军用卫星导航接收机现状及发展趋势［J］．现代导航，2014（1）：58－61．

［5］ HWANG P Y C．Kinematic GPS for Differential Positioning：Resolving Integer Ambiguities on the Fly［J］．Navigation，1991，38（1）：1－15．

［6］ CHEN D．Fast Ambiguity Search Filter（FASF）：A Nova1Concept for GPS Ambiguity Resolution［C］．Proceedings of the 6th International Technical Meeting of the Satellite Division of The Institute of Navigation （ION GPS 1993）．1993：781－787．

［7］ HATCH R，SHARPE T．A Computationally Efficient Ambiguity Resolution Technique［C］．Proceeding of ION GPS 2001：11－14．

［8］ 蔡艳辉，程鹏飞，李夕银．整周模糊度去相关的两种实现方法［J］．测绘工程，2003，12（4）：36－38．

［9］ 朱志宇，刘维亭，张冰．差分GPS载波相位整周模糊度快速解算方法［J］．测绘科学，2005，30（3）：54－57．

［10］陈树新，王永生．一种消除GPS模糊度相关性的新算法［J］．航空学报，2002，23（6）：542－546．

［11］高成发．GPS事后相位差分坐标解算模型及其相关问题的研究［J］．测绘学报，2006，35（2）：148－148．

［12］兰孝奇，张兵良，黄继红，等．GPS伪距差分定位技术的试验研究［J］．河海大学学报（自然科学版），2004，32 （3）：300－303．

［责任编辑：刘文霞］

Research on the recovery method of GPS cycle slips based on carrier phase

LYU Zhenyang，LIU Bohong，FU Yuming

（School of Automatic and Electrical Engineering，Lanzhou Jiaotong University，Lanzhou 730070，China）

Abstract：Cycle slip detection and repair is the prerequisite for obtaining high－precision positioning results in GPS positioning．Many methods have been proposed for the question of detection and repair of the cycle slips data in carrier phase，but they all have their own shortcomings．Aiming to accurate positioning fast with three satellites when the date generate cycle slips，this paper propose a new method to define the integer ambiguity，through construction equations by using multiple epochs data，for the carrier phase positioning in harsh environments．

Key words：GPS；carrier phase；cycle slips；integer ambiguity

作者简介：吕振扬（1990－），男，硕士研究生．

收稿日期：2015－05－26

中图分类号：P228

文献标识码：A

文章编号：1006－7949（2016）01－0021－03