基于二分图的疾病与中药关联性研究*
李梦箐,朱友泽,马 利,胡 芳
(湖北中医药大学信息工程学院 武汉 430065)
基于二分图的疾病与中药关联性研究*
李梦箐,朱友泽,马 利,胡 芳**
(湖北中医药大学信息工程学院 武汉 430065)
目的:本研究基于二分图对疾病和中药之间的关联性进行分析,构成“疾病-中药”的复杂网络模型。 方法:首先,根据每种疾病对应方剂中的中药分别构建疾病数据库与中药数据库,计算出每种疾病和中药所对应的度数;其次,运用Jaccard相似度函数建立中药关联性,并根据中药关联性推断出疾病关联性;最后,利用二分图和复杂网络方法对疾病与中药之间的关系进行分析,并用PAJEK软件进行仿真实验。结果:得出疾病与中药、疾病与疾病、中药与中药、证候与中药之间的二分图关系。结论:通过对实验结果进行分析,得出药物和疾病相关性结论,并进一步提出在以后研究中采用二叉树建立“疾病-中药”数据库,以便后期对数据进行关联分析。
疾病 方剂 中药 二分图 数据建模
21世纪已进入大数据时代,数据挖掘的重要性日益显现[1]。在中医药研究领域,很多研究方法都用到了数据挖掘。杨铭等[2]将复杂系统熵网络方法应用到中医肿瘤临床数据中。沈洪等[3]提出了基于数据挖掘的溃疡性结肠炎核心中药和配伍分析,林基伟等[4]用数据挖掘的方法总结名老中医黄春林治疗慢性肾炎的用药经验。将疾病看作方剂组成事务项,并在此基础上进行分类、聚类、关联等分析,挖掘出的潜在信息对中医药研究具有非常重要的意义[5]。
二分图又称作二部图,是图论中的一种特殊模型。目前二分图的应用非常广泛,例如工业制造、农产品生产、航空航天工业等等,应用最广泛于人际关系网,应用二分图匹配法对大数据集进行分析[6]。Cui Y Z等[7]提出了一种在二分图中发现重叠社团结构的算法,Li K等[8]提出了一种基于模块度值的二分图划分算法。目前,通常有两种二分图研究方法,一种是基于原始的二分图进行网络分析,一种是投影的方式,将二分图投影到单层网,然后进行网络分析[9-12]。由于方剂是疾病与中药之间的桥梁,因此本研究通过对方剂中药构成的研究,采用确定性二分图投影的方式,构建疾病与中药之间关联性的二分图网络,并在此基础上进行分析和探讨,深入挖掘疾病和中药之间的潜在联系。
1 分析数据和二分图介绍
1.1 疾病和中药数据
方剂学运用实验研究的手段,从实证的角度认识疾病与方剂中药之间的配伍关系[13],中医辩证治疗是中医学的核心,在基础理论指导下按照中药配伍原则辩证施治,选择合适中药并斟酌用量。方剂共有19种剂型,参照汪氏分类法共可以分21类,具体数目不确定,因为根据不同的中药加减配伍会有不同的变化,也就有了不同的方剂。生物谷数据中心提供的数据表明,方剂数据库信息列表共有84 449种方剂,所治疗的疾病近万种[14]。本研究通过对疾病对应方剂中的中药原始数据进行整理解决中药同名异物、同物异名等术语不规范问题,并构建“疾病-中药”矩阵。本研究的研究数据来源于三大科室(外科、内科、皮肤科)中常见的28种疾病(包括肝病的相关数据)和治疗这些疾病所需要的常用185种中药。
1.2 二分网络投影方法介绍
用二分图G=(X,Y)来表示一个二分网络,其投影方法也分为两类:加权和无权投影。例如,对一类节点,比如X类节点,无权投影的规则是:如果两个X类节点有至少一个公共的邻居(Y类节点),那么这两个节点之间有连边,无权投影所得网络只能给出一类节点之间是否存在边(是否合作过),无法描述节点之间的合作强度,也就是说无权单顶点网络无法给出两个同类节点之间的合作强度,造成了信息的丢失,两类二分图如图1所示。
图1可简单定义为G(V,E),其中,V、E分别表示点和边的集合,二分图亦可以理解为因果图的一个特例[15]。二分图中所有节点按照各自属性分为两类节点,本研究中分别是疾病类和中药类。权值不同二分图也可以分为确定性二分图和非确定性二分图两类[16]。根据对确定性二分图的定义,原因与结果之间因果关系即疾病与中药之间的关系,只有两种:若为1表示具有必然导致关系;若为0表示因果没有联系。
1.3 疾病与中药的度计算

图1 两类二分图
疾病与中药的关联性主要根据中药之间的关联进行连接。由于中医和西医具有很大的区别,用中药治疗西医分类的疾病需要具体看临床反应。如一些病人虽然疾病相同,但是体质不同,所需要的中药也会有所区别。本研究重点针对三大科室(外科、内科、皮肤科)中常见的28种疾病所需要的常用185种中药数据进行分析,通过这些中药去深入挖掘疾病之间的隐性关联性。在数据建模过程中,对疾病和中药关联性分析都是建立在无中药加减、无药引的情况下建立的。疾病的度的计算是根据与之关联的中药多少来计算的,例如疾病节点“痛风”与“大川乌、黑豆、全虫、地龙、麝香”等5种中药关联,因此该节点的度是5;中药节点“桔梗”与“冠心病、偏头痛、急性肺炎、肩周炎、黄褐斑”等5种疾病关联,因此该节点的度是5,依次方式,分别计算出28种疾病和185种中药的度,分别如图2和3所示。
从图2可以看出,不同的疾病对应中药的度相差较大,其中脚气对应的中药最多。大多数疾病对应的中药数量集中在8-16之间。

图2 疾病的度计算结果图
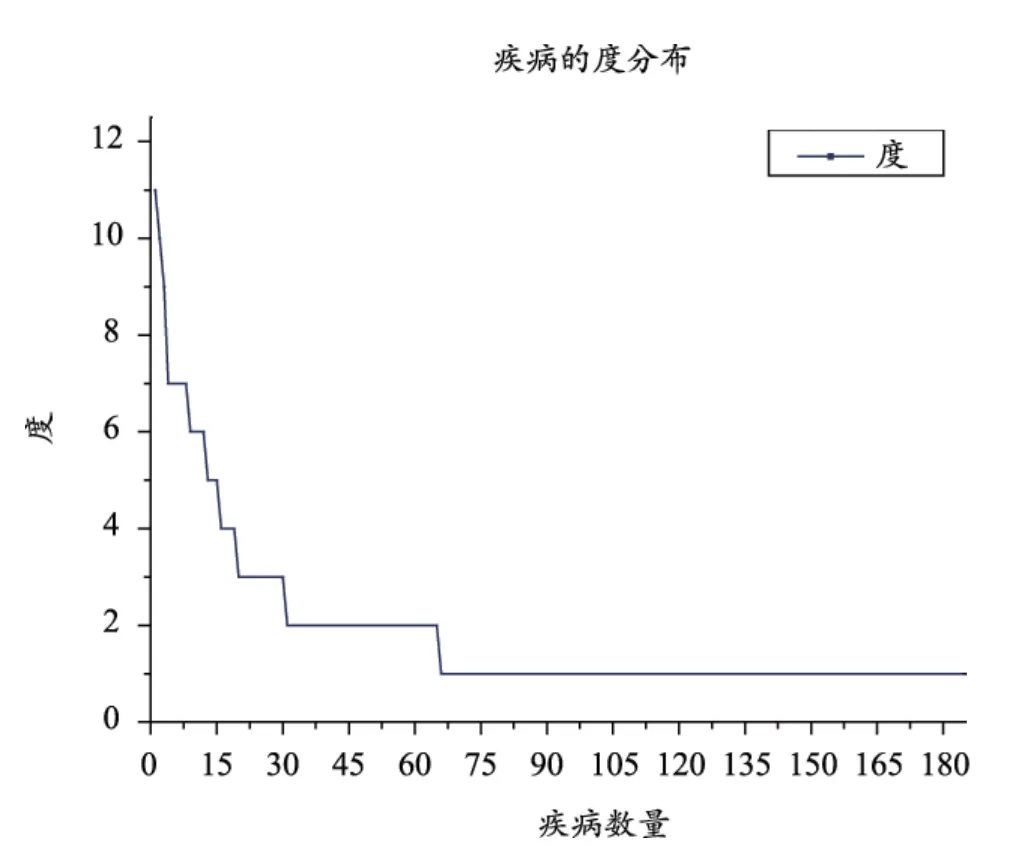
图3 中药的度计算结果图
从图3看出,大多数的中药只对应一种疾病,只有少数几种常用中药可以对应多种疾病甚至超过10种疾病如枳壳、丹参、当归等。
2 疾病-中药关联性二分网络图
2.1 疾病-中药关联性二分网络图构建思想
由于疾病与中药之间的关系,符合构建二分图的构建的条件,即疾病之间不连接,中药之间不连接,疾病与中药之间连接等特点。因此,为了研究疾病之间及中药之间的这种潜在的关联性,选择二分图投影方法,构建疾病-中药关联性二分网络图。并在此基础上,深入分析中药之间及疾病之间的隐形关联,虽然疾病节点之间虽然没有直接相连,但通过中药节点之间的联系可以建立疾病之间的隐性关联。同理,可以建立中药之间的隐形关联。在构建疾病-中药关联性二分网络图过程中,采用无权投影方法,即两个疾病中至少有一个中药相同,则两个疾病节点有连边。
本研究将西医中分类的科室和疾病,找到所治疗的方剂和包含中药,挖掘两者之间潜在关系,算出阈值。采用二分图分类分析,将疾病和中药分为两类,首先,分别计算出它们的度,其次,采用基于Jaccard相似度的算法[17]计算各中药之间的关联度。Jaccard相似度用来比较样本集中的相似性和分散性的一个概率。在本研究中,其中X、Y表示两种中药,|X∩Y|表示X和Y共同方出现的次数,|X∩Y|表示X组方次数和Y组方次数之和。Jaccard相似度能够很好地描述个体相似性。
2.2 疾病-中药关联性二分网络构建步骤
以下是疾病与中药关联性二分网络构建步骤:
步骤1:疾病和中药的关联式性是确定性的,疾病发生中药肯定使用,概率为1,所以本研究使用确定性二分图进行研究,该确定性二分图有3种元素组成:
①疾病发生源集合T=(t1, t2, ……, tm),T中元素取值为1表示疾病假定发生,取值为0表示疾病假定未发生。
②中药使用集合C=(c1, c2, ……, cn),C中元素取值为1表示相应的中药假定使用,取值为0表示中药假定未使用。
③按照二分图定义,疾病集合T=(t1, t2, ……, tm),中药集合C=(c1, c2, ……, cn),关系矩阵rij表示疾病和中药之间的因果关系。矩阵关系如下:

c1c2…cnt1r11r12…r1nt2r21r22…r2n……………tmrm1rm2…rmn
m×n的关系举证R表示疾病和中药之间的因果关系。R中元素rij=1表示疾病ti发生将导致中药cj的使用;rij=0表示疾病ti不发生不会导致中药cj的使用。
步骤2:求解T集合中2个元素关系,设关系值为a,b,c,d:
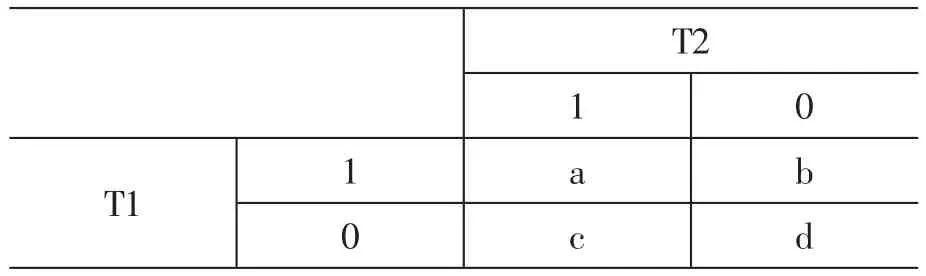
T2 1 0 T1 1 a b 0 c d

3 疾病-中药关联性结果分析
疾病-中药关联二分网络如图4所示,其中,黄色节点代表中药(185个),绿色节点代表疾病(28个),蓝色直线连接中药和疾病之间的直接作用关系。
二分图中节点度是指该节点连边的数量,中药节点的度表示与其相关的疾病个数,疾病节点的度表示与其相关的中药个数。从图4可以看出来,疾病节点(脚气)度最大为23,表示该疾病共引用中药23种,中药节点(枳壳)度最大为40。统计图4中节点的度发现,度数为1的中药占总数的64.86%(120/185),度数为2的占总数的37.84%(70/185)。说明大部分的中药被引用1次或者2次。只有少数中药被引用多次,如枳壳和丹参。
图5包含185个节点(中药),1 421条边,其中,有4孤立节点,分别是大川乌、麝香、黑豆、全虫。
图6包含28个节点(疾病)、242条边,其中,有1孤立节点“痛风”,说明此疾病和其他疾病在中药治疗上没有任何关联。网络的平均度为24.43,说明一个疾病与多个疾病存在潜在相关性。

图4 疾病-中药关联网络示意图

图5 185种中药关联图

图6 28种疾病关联图

图7 中药-证候关联网络示意图
证候-中药关联二分网络如图7所示,其中,和T2之间的简化公式:黄色节点代表中药(14个),绿色节点代表证候(144个),蓝色直线连接中药和证候之间的直接作用关系。
从图7可以看出来,中药(大黄)度最大为16,表示该中药可对应16种证候。统计图7中节点的度发现,度数为11的中药占总数的50%(7/14),度数为10的占总数的21. 43%(3/14)。
4 结论
本研究针对外科、内科和皮肤科的常见疾病和对症中药之间的关联性进行研究,构建28种疾病和185种中药的二分图网络模型,归类算出疾病和中药的节点度;根据节点关联度算出集聚系数,疾病之间通过中药的关联进行联系,计算出关联度较强的几种疾病,并对疾病-中药关联网络图进行深入分析,预测或挖掘疾病之前潜在的关联性和中药之间的关联性。
在未来的研究工作中,可进一步将中药名进行规范化处理,可以尝试用二叉树来建立中药名数据库。后期如若增加节点,可以在原模型上增删、择优,“疾病-中药”扩展图上挖掘更多的信息或者进行更多的算法研究,可以尝试中药社团和疾病社团划分,中药性质作用机制等方面的研究。
1 孟凡红,万芳,张早华,等.关于中医药信息化建设与发展的思考.世界科学技术-中医药现代化, 2011, 13 (3): 461-465.
2 杨铭,焦丽静,陈佩奇,等.复杂系统熵网络方法及其在中医肿瘤临床数据挖掘中的应用.世界科学技术-中医药现代化, 2012, 14(2): 1376-1383.
3 沈洪,叶柏,张露,朱磊,等.基于数据挖掘的溃疡性结肠炎核心中药及配伍分析.世界科学技术-中医药现代化, 2013, 15(5): 926-931.
4 林基伟,邹川,刘旭生.基于数据挖掘方法总结黄春林名老中医治疗慢性肾炎的用药经验.世界科学技术-中医药现代化, 2015, 17(2): 382-388.
5 李明,佟琳,张维娜,等.汉唐止痛方剂的复杂网络方法分析.中医药信息, 2012, 29(3): 22-24.
6 Wasseraman S, Faust K. Social Network Analysis: methods and applications. Cambridge:Cambridge University Press. 1994: 188-194.
7 Cui Y Z, Wang X Y. Uncovering overlapping community structures by the key bi-community and intimate degree in bipartite networks. Physica A: Statistical Mechanics and its Applications, 2014, 407: 7-14.
8 Li K, Pang Y. An unified community detection algorithm in complex network. Neurocomputing, 2014, 130: 36-43.
9 BaraAsi A L, Albert R. Emergence of scaling in random networks. Science, 1999, 286(5439): 509-512.
10 Newman M E. Scientific collaboration network.Network construction and fundamental results. Phys Rev E Stat Nonlin Soft Matter Phys, 2001, 64(1 Pt 2): 016131.
11 王进良,张鹏,递增如,等.北京师范大学图书借阅系统的网络分析.情报学报, 2009, 28(1): 137-141.
12 Lambiotte R, Ausioos M. Uncovering collective listening habits and music genres in bipatite networks. Phys Rev E Stat Nonlin Soft Matter Phys, 2005, 72(6 Pt 2): 066107.
13 何阅,张培培,唐继英.中药方剂的合作网络描述.科技导报, 2005, 23(11): 36-39.
14 孙正.基于药物属性的中药方剂组网及药物社团发现研究.南京:南京大学硕士学位论文, 2013: 18-29.
15 李楠楠,张宁.图书馆借阅网的二分图研究.复杂系统与复杂性科学, 2009, 6(2): 33-39.
16 蔡莹莹.基于二分图的应急预案体系有效性研究. 大连:大连理工大学硕士学位论文, 2012: 8-10.
17 刘正.基于MapReduce的中药数据网络化及挖掘. 南京:南京大学硕士学位论文, 2012: 23-26.
An Association Study on the Correlation Between Diseases and Herbal Medications Based on Bipartite Graph
Li Mengqing, Zhu Youze, Ma Li, Hu Fang
(Information Engineering Institute, Hubei University of Chinese Medicine, Wuhan 430065,China)
Bipartite graph is a special model in the graph theory with the characteristics of clustering andassociativity. In this study, the analysis of the correlation between diseases and herbal medications was performed based on bipartite graph before constructing the “Disease-Herb” complex network model. Firstly, the disease database and herb database were established in which the diseases and their prescriptions were involved. After that, the degrees of diseases and herbs were calculated separately. Secondly, the correlation among herbs was analyzed through the “Jaccard” similarity function, and so was the correlation of diseases. Finally, the correlation between diseases and herbal medications was deduced via the methods of bipartite graph and complex network; and the simulate experiment was implemented by “Pajek” software. As a result, the correlations of diseases and herbal medications, diseases and diseases, herbs and herbs, and syndromes and herbs were obtained. It was concluded that the correlation between diseases and herbal medications can be drove through data analysis. The binary tree method should be reasonably used to establish a “Disease-Herb” database in the future to analyze the correlations conveniently.
Disease, prescription, herb, bipartite graph, data modeling
10.11842/wst.2016.04.004
R283.6
A
(责任编辑:马雅静,责任译审:朱黎婷)
2015-09-28
修回日期:2015-10-09
* 2014年湖北中医药大学校级教学研究项目(2014B17):医学信息工程专业学生数据建模能力培养模式研究,负责人:胡芳;2014湖北省教育厅科学研究计划项目(D20152003):基于肝病的中医临床术语本体构建研究,负责人:马利。
** 通讯作者:胡芳,讲师,博士,主要研究方向:医学信息学,复杂网络与复杂系统。

