区间灰色不确定语言多属性群决策方法*

韩二东，郭　鹏，赵　静西北工业大学管理学院，西安710072

* The National Natural Science Foundation of China under Grant Nos. 71272049，71402142（国家自然科学基金）; the Specialized Research Fund for the Doctoral Program of Higher Education of China under Grant No. 20126102110052（高等学校博士学科点专项科研基金）; the Humanities，Social Science and Management Research Foundation of Northwestern Polytechnical University under Grant No. 3102014RW0008（西北工业大学人文社科与管理研究基金）.

Received 2015-03，Accepted 2015-05.

CNKI网络优先出版：2015-05-29，http://www.cnki.net/kcms/detail/11.5602.TP.20150529.1608.002.html

ISSN 1673-9418 CODEN JKYTA8

Journal of Frontiers of Computer Science and Technology

1673-9418/2016/10（01）-0093-10



区间灰色不确定语言多属性群决策方法*

韩二东＋，郭鹏，赵静
西北工业大学管理学院，西安710072

* The National Natural Science Foundation of China under Grant Nos. 71272049，71402142（国家自然科学基金）; the Specialized Research Fund for the Doctoral Program of Higher Education of China under Grant No. 20126102110052（高等学校博士学科点专项科研基金）; the Humanities，Social Science and Management Research Foundation of Northwestern Polytechnical University under Grant No. 3102014RW0008（西北工业大学人文社科与管理研究基金）.

Received 2015-03，Accepted 2015-05.

CNKI网络优先出版：2015-05-29，http://www.cnki.net/kcms/detail/11.5602.TP.20150529.1608.002.html

ISSN 1673-9418 CODEN JKYTA8

Journal of Frontiers of Computer Science and Technology

1673-9418/2016/10（01）-0093-10

E-mail: fcst@vip.163.com

http://www.ceaj.org

Tel:＋86-10-89056056

Key words: multi-attribute group decision making; grey fuzzy number; information entropy; interval grey uncertain linguistic variables; geometric aggregation operator

摘要：针对属性值为区间灰色不确定语言信息的多属性群决策问题，在定义区间灰色不确定语言变量及其运算规则的基础上，给出了3种几何加权集结算子，由区间灰色不确定语言几何加权算子集结各决策者给出的决策矩阵得到群体决策矩阵。在属性权重已知的情形下，基于该算子集结单个决策者给出的属性权重向量得到群体属性权重向量；在属性权重完全未知的情形下，采用信息熵法确定属性权重向量。采用区间灰色不确定语言混合几何加权算子集结各属性评价信息，得到各方案的综合评价值，基于区间灰色不确定语言变量大小比较的方法得到方案排序结果。算例分析表明了该方法的有效性与可行性。

关键词：多属性群决策；灰色模糊数；信息熵；区间灰色不确定语言变量；几何集结算子

1　引言

多属性群决策是将群体中各决策者对有限方案的多个属性评价信息按照某种规则集结为一致或妥协的群体偏好序[1-4]。在实际决策过程中，决策专家对诸如干部考核与选拔、风险投资公司投资方案选择、经济效益评价等决策对象进行评价判断时，决策问题往往表现出复杂性与不确定性。此外，由于不同决策专家知识水平、经验和对事物认知能力的差异使得评价信息具有不完全性[5-6]，导致决策问题兼具有模糊性与灰色性的双重特点，即为灰色模糊的多属性群决策问题[7-8]。针对模部为精确数的灰色模糊多属性决策问题，文献[9]将灰色模糊数评价信息的模部与灰部统一转化为区间数，由区间数排序方法对备选方案排序择优；文献[10]采用理想点法，通过计算各方案到理想方案的模糊距离得到方案排序结果；文献[11]基于熵权法确定属性权重，综合灰色模糊数的模部与灰部集结每个方案的各属性评价信息。精确数表示的模部对决策问题的模糊性体现不够充分，使得决策信息背离了备选方案本身的复杂性及决策思维的模糊性。此后，文献[12]使用区间数表示模部，依然采用精确数表示灰部；文献[13]统一使用区间数表示模部与灰部，由有序加权平均算子集结各属性评价信息得到方案的综合评价值；文献[14]采用语言短语表示模部，区间数表示灰部，在定义区间灰色语言变量及其运算规则的基础上，给出了区间灰色语言变量混合几何集结算子，基于几类集结算子对评价信息进行集结；文献[15]将语言短语表示的模部转化为二元语义，在属性权重不完全已知的条件下，给出了基于灰色关联分析的灰色模糊多属性群决策方法；与文献[14-15]均采用区间数表示灰部不同，文献[16]采用三参数区间数表示灰部，提出了一种基于投影模型的三参数区间灰色语言变量多属性群决策方法。根据语言短语与不确定模糊数的对应转换关系，文献[17]将语言变量表示的模部转化为三角模糊数，提出了一种基于平均相似度且带有主观偏好的多属性群决策方法；文献[18]将模部转化为梯形模糊数，在定义区间灰色梯形模糊数运算规则及其距离的基础上，采用灰色关联法得到了方案的排序结果。以上研究针对灰色模糊数模部与灰部的不同表达（区间数、语言短语、二元语义等），分别采用了有效的确定属性权重的方法，在定义信息集结算子及其运算规律的基础上，对各决策者给出的灰色模糊评价信息进行集结，从而得到各方案的优先序。

与语言短语表达的模部相比，不确定语言变量更能体现决策问题的复杂性及现实环境的不确定性，同时考虑到决策专家对评价对象认知的局限性，决策者更可能给出区间灰色不确定语言评价信息。基于此，本文针对具有区间灰色不确定语言评价信息的多属性群决策问题，采用不确定语言变量表达模部，采用区间数表示灰部，给出区间灰色不确定语言变量的定义、运算性质、相互之间距离及大小比较的方法；针对属性权重已知及完全未知两种不同的情形，在定义3类几何加权集结算子的基础上提出了群决策方法，并将该群决策方法应用到移动银行服务质量评估问题中。

2　预备知识

2.1区间灰色不确定语言变量的定义及运算

假设语言评价集为S＝{s0，s1，…，sT}，T为偶数，其粒度为T＋1，例如粒度为7的语言评价集定义为S＝{s0＝非常差，s1＝很差，s2＝差，s3＝中等，s4＝好，s5＝很好，s6＝非常好}。关于语言评价集的有序性、存在逆算子、极大化运算、极小化运算等性质，这里不再赘述。语言评价集中的语言短语si与其下标i之间存在严格单调递增关系，设下标函数为i＝f（si），若si≤sj，则有i＜j，反之亦然；下标函数的反函数为si＝f−1（i），若i＜j，则有si≤sj，反之亦然，即下标函数与其反函数均为严格单调递增函数。为最大限度地减少评价信息的丢失，将定义的离散语言评价集S拓展为连续语言评价集，即ST＝{sα|α∈[0，T]}，拓展后的语言评价集ST仍然满足严格单调递增关系，且相关的运算性质保持不变。

设sα、sβ为ST中的语言变量，且α≤β，则[sα，sβ]为不确定语言变量[19]，区间的两端点分别为不确定语言变量的下限和上限。当α＝β时，不确定语言变量退化为连续语言评价集中的语言变量。

模部反映评价信息的模糊性及不确定性，灰部反映评价信息所造成的灰色性。灰部的灰度越大表示决策者给出的评价信息的可信度越低，可利用的信息量越少，当灰度大到一定程度时，决策者给出的评价信息完全丧失价值，对方案评价不起作用；反之，灰度越小表示信息可利用价值越大，信息可靠性越高。在灰色模糊集定义的基础上，给出如下区间灰色不确定语言变量的定义。

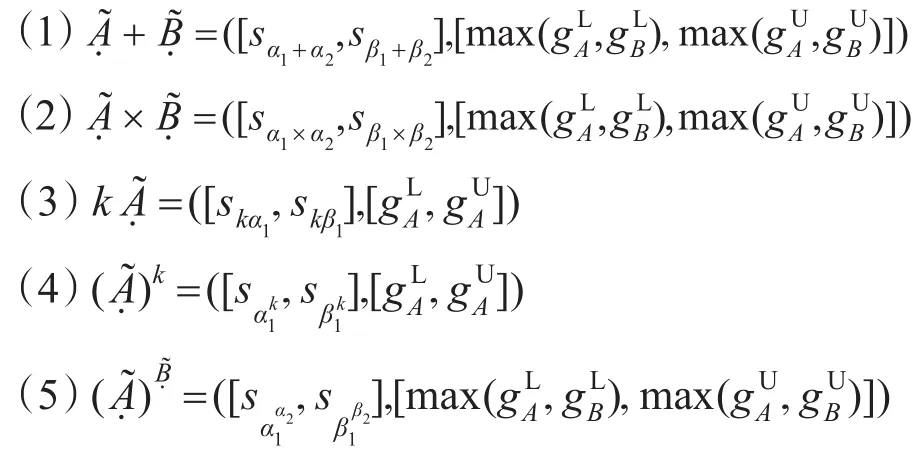
2.2区间灰色不确定语言变量之间的距离及大小比较

定义2两个区间灰色不确定语言变量之间的Hamming距离为：

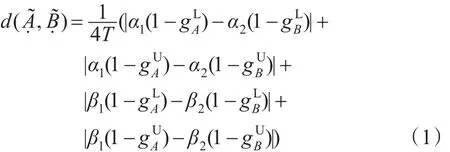
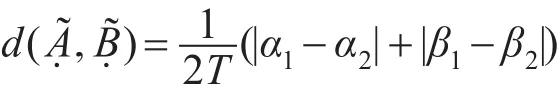
定义3[20]设[a，b]为区间数，连续区间数有序加权平均（continuous interval ordered weighted averaging，C-OWA）算子定义为：

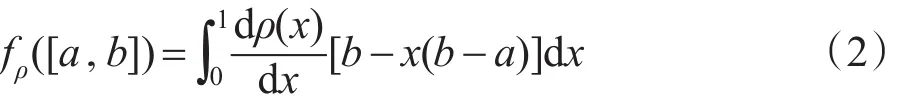
其中，函数ρ（x）:[0，1]→[0，1]为基本单位区间单调（basic unit-interval monotonic，BUM）函数，满足ρ（0）＝0，ρ（1）＝1，当x1＜x2时，有ρ（x1）≤ρ（x2）。令ρ（x）＝xr（r≥0），可得fρ（[a，b]）＝。

定义4设[sα1，sβ1]为不确定语言变量，连续区间二元语义的有序加权平均（continuous interval two-tuple ordered weighted averaging，ITC-OWA）算子定义为：

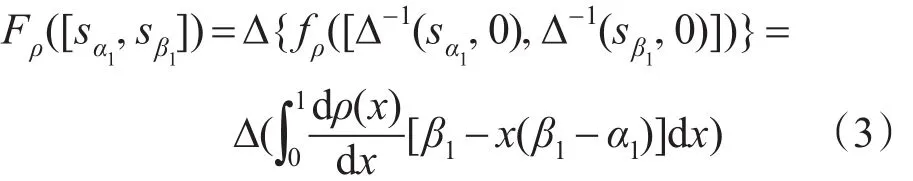
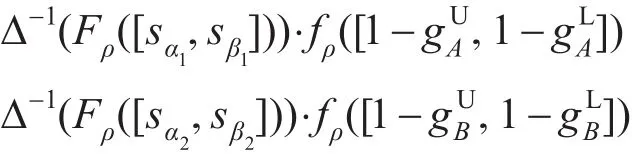
3　区间灰色不确定语言变量几何加权集结算子

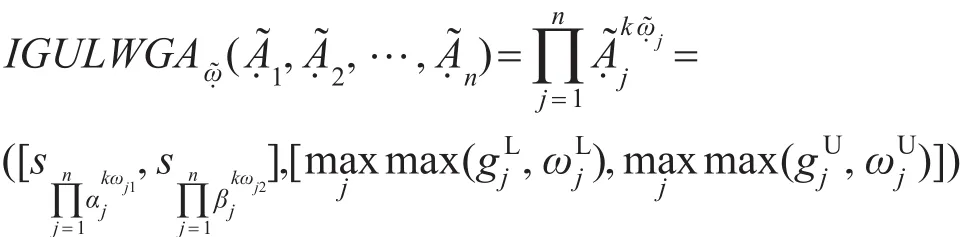
称IGULWGA（interval grey uncertain linguistic weighted geometric aggregation）为区间灰色不确定语言几何加权集结算子。其中，Ω为全体区间灰色不确定语言变量的集合；͂＝͂1，͂2，…，͂n）是这组区间灰色不确定语言变量的权重向量，为的权重，也是区间灰色不确定语言变量，即＝（[sωj1，sωj2]，[，]），j＝1，2，…，n；k为调节系数，一般取为1/T。

该算子是对给定的区间灰色不确定语言变量自身的重要性程度进行加权集成，权重与是一一对应的。

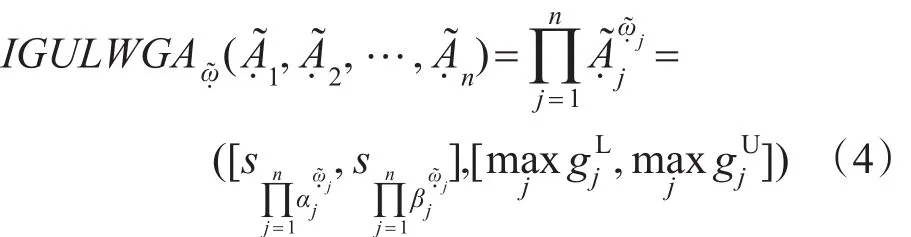
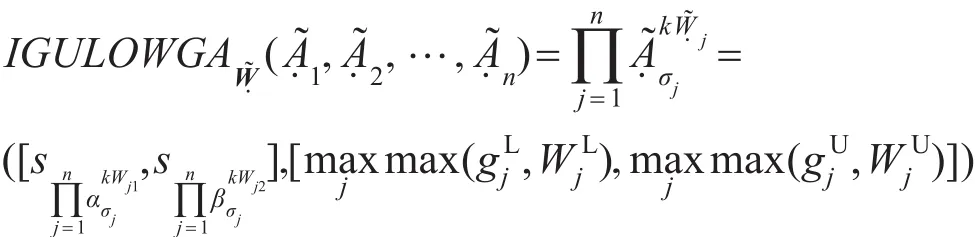
称IGULOWGA（interval grey uncertain linguistic ordered weighted geometric aggregation）为区间灰色不确定语言有序几何加权集结算子，其中͂＝͂1，͂2，…，͂n）是与算子相关的区间灰色不确定语言加权向量，即͂j＝（[sWj1，sWj2]，[，]），j＝1，2，…，n；（σ1，σ2，…，σn）为（1，2，…，n）的一个置换，使得对于任意的j，有≥，即j是所有中第j大的元素；k为调节系数，一般取为1/T。

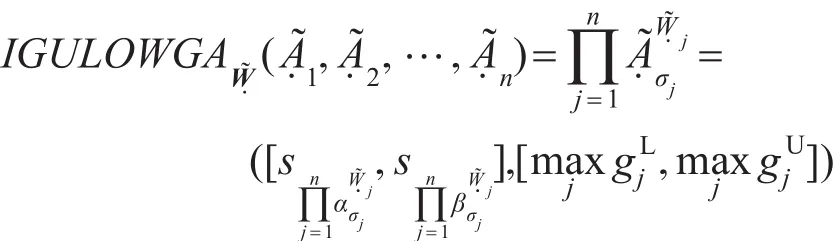
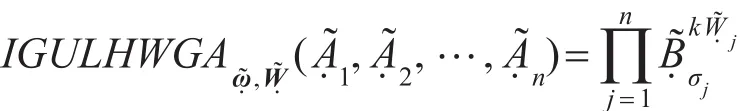
称IGULHWGA（interval grey uncertain linguistic hybrid weighted geometric aggregation）为区间灰色不确定语言混合几何加权集结算子。其中͂＝͂1，，…，͂n）是与算子相关的区间灰色不确定语言加权向量，即͂j＝（[sWj1，sWj2]，[，]），j＝1，2，…，n；͂＝͂1，͂2，…，）为͂j（j＝1，2，…，n）的权重向量，其各分量均为区间灰色不确定语言变量，即͂j＝（[sωj1，sωj2]，[，]），令：

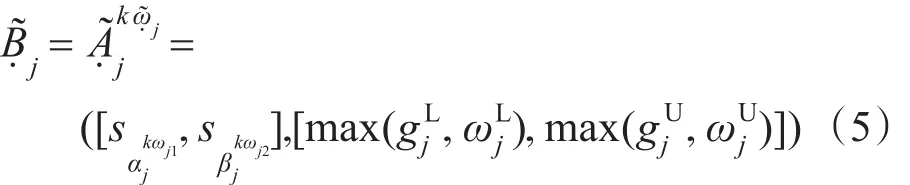
其中，k为调节系数，一般取为1/T；（σ1，σ2，…，σn）为（1，2，…，n）的一个置换，使得对于任意的j，有≥。

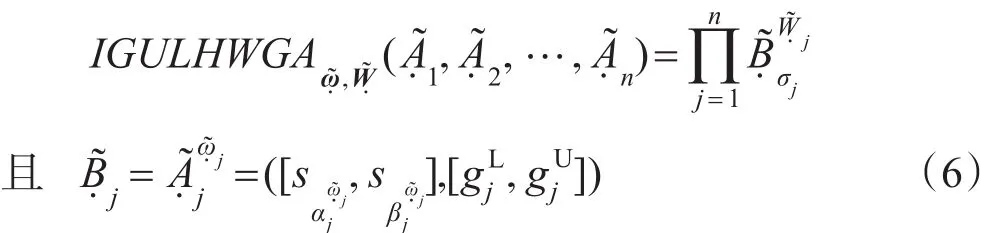
4　基于几何加权集结算子的多属性群决策方法

4.1问题描述

在多属性群决策问题中，设专家集为E＝{ek|k＝1，2，…，p}，决策方案集为C＝{ci|i＝1，2，…，m}，属性集为U＝{uj|j＝1，2，…，n}，决策者ek选择粒度为T＋1的语言评价集，对决策方案ci关于属性uj进行测度，属性评价值采用区间灰色不确定语言变量表示为：

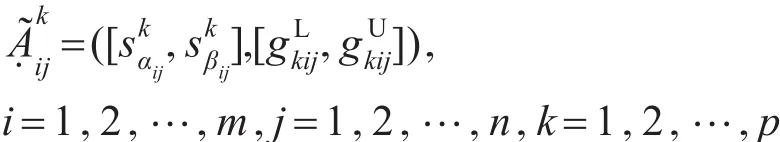
本文要解决的是具有区间灰色不确定语言变量的多属性群决策问题，依据决策矩阵及决策者权重并在属性权重已知及完全未知两种不同的情形下实现对方案的排序择优。

4.2群决策步骤

步骤1群体决策矩阵的集成。

每个决策者对不同方案关于所有属性进行评价，给出各自的决策矩阵，k＝1，2，…，p，根据决策者权重向量ωe，由IGULWGA算子得到群体决策矩阵A＝）m×n，其中：

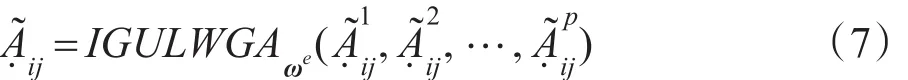
步骤2属性权重的确定或集成。

（1）针对属性权重已知的情形，根据决策者权重向量ωe及单个决策者给出的属性权重向量＝），其中），j＝1， 2，…，n，k＝1，2，…，p，由IGULWGA算子得到群体属性权重向量），其中：

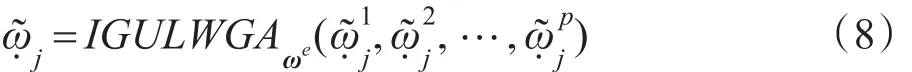
（2）针对属性权重未知的情形，采用信息熵法确定属性权重。信息熵可用来度量两离散概率分布的偏差程度[21-22]，是信息不确定性的一种度量。若所有方案对某属性的评价偏差越大，则该属性所确定的信息熵就越小，所包含的信息量就越大，该属性对方案排序所起的作用就越大，应赋予越大的权重。根据所有方案对某属性的评价偏差大小与该属性权重大小的一致性确定属性权重，即偏差越大的属性应赋予越大的权重。特别地，若各方案对某属性的评价值无差异，则该属性对方案排序择优不起任何作用，其权重应当为0。基于此，方案ci与其他所有方案关于属性uj的评价偏差为：

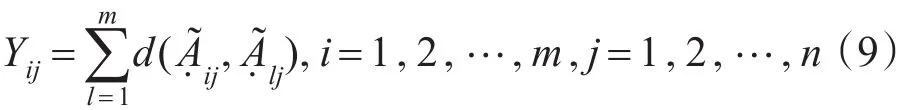
则每个方案与其他所有方案关于属性uj评价值的总偏差为：

属性uj的信息熵值表示为：

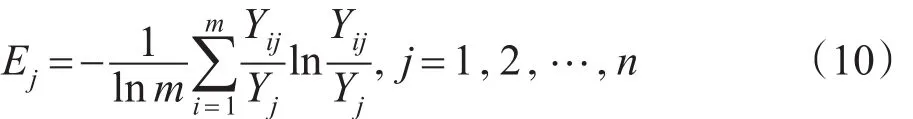
从而确定属性uj的权重为：

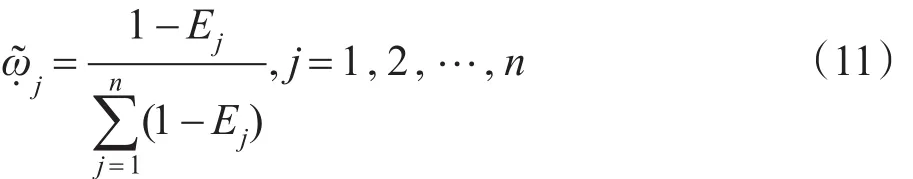
步骤3由IGULHWGA算子计算每个方案的综合评价值。

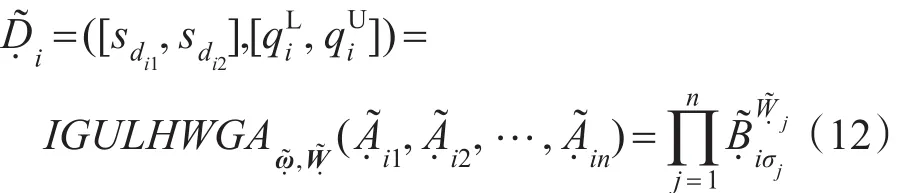
步骤4对各方案的综合评价值进行比较得到各方案排序结果。

每个方案的综合评价值仍然为区间灰色不确定语言变量，由综合评价值的代表数值Di＝∆−1（Fρ（[sdi1，sdi2]））⋅fρ（[1−，1−]）对所有方案排序，代表值越大，方案越优。

5　算例分析

移动银行网站服务质量的高低直接影响客户对移动银行的美誉度与忠诚度，对移动银行的经济效益产生巨大影响，同时也是移动商务运营商成功的关键因素。基于此，采用本文群决策方法对移动银行服务质量进行评估。现有3位相关领域专家，即E＝{e1，e2，e3}，分别从服务场景（u1）、易于使用程度（u2）、服务信息质量（u3）及信息安全性（u4）这4个指标对4个移动银行服务质量进行评估，即C＝{c1，c2，c3，c4}，专家权重向量为ωe＝（0.3，0.4，0.3）。3位决策专家均采用7粒度（即T＝6）的语言评估标度，即S＝{s0，s1，s2，s3，s4，s5，s6}，针对各方案的每个属性给出如表1～表3所示的灰色不确定语言评价信息。

由式（4）、式（7）将3位决策专家给出的评价信息进行集结，得到群体决策矩阵A＝͂ij）4×4即：

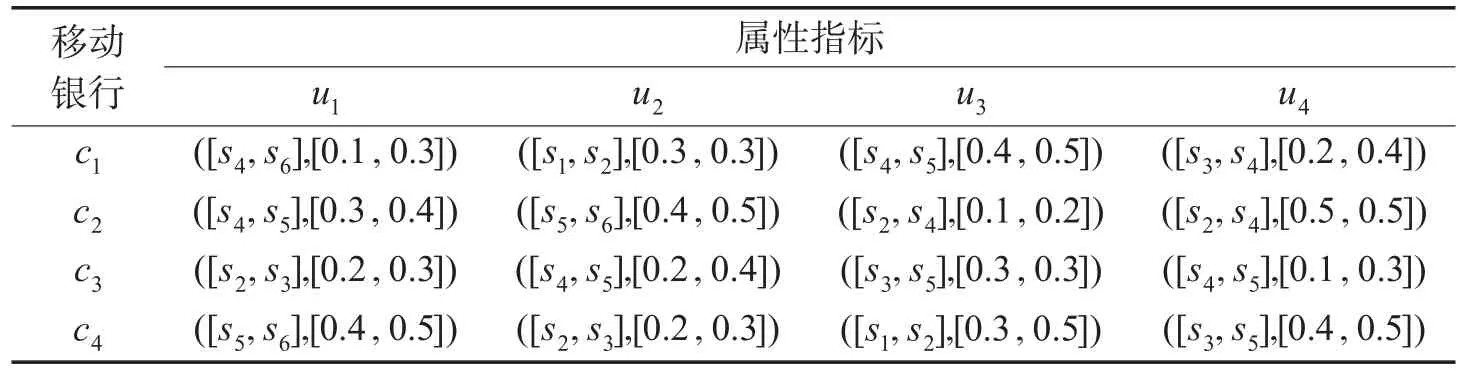
Table 1 Evaluation values of different attribute indexes of four mobile banks given by decision expert e1表1　决策专家e1给出的4个移动银行不同属性指标的评价值

Table 2 Evaluation values of different attribute indexes of four mobile banks given by decision expert e2表2　决策专家e2给出的4个移动银行不同属性指标的评价值

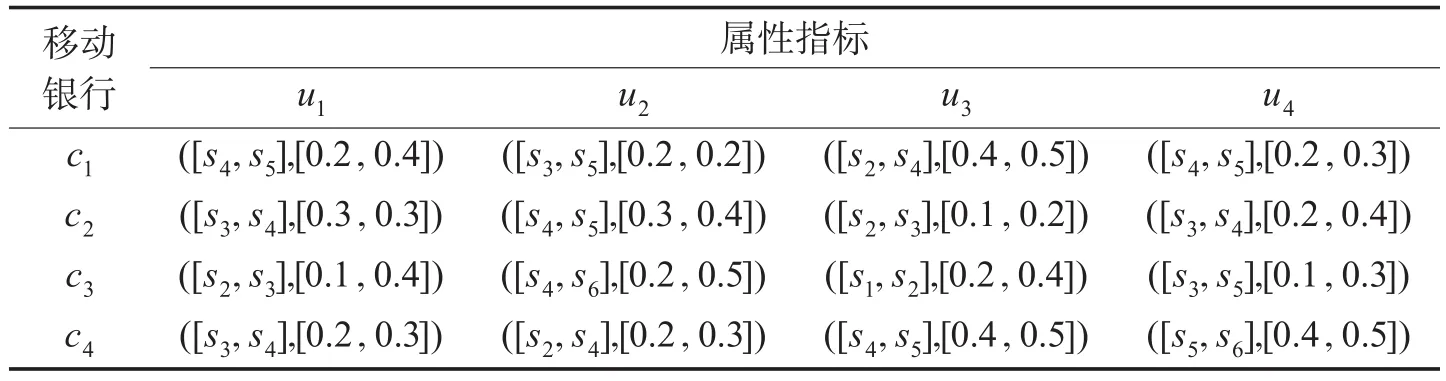
Table 3 Evaluation values of different attribute indexes of four mobile banks given by decision expert e3表3　决策专家e3给出的4个移动银行不同属性指标的评价值

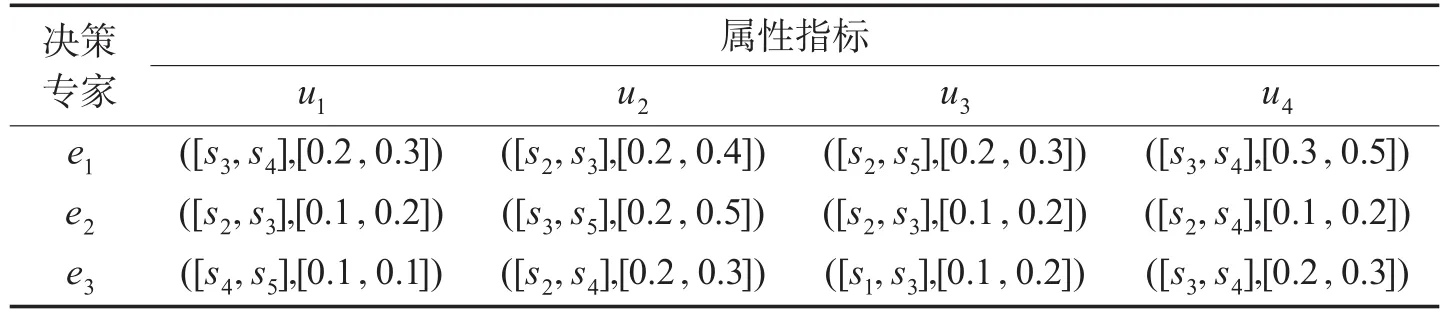
Table 4 Weight values of attribute indexes given by three decision experts表4　3位决策专家给出的属性指标权重值

5.1属性权重已知的情形

针对属性权重已知的情形，假设3位决策专家给出的属性权重值如表4所示。

由式（8）得到群体属性权重向量为：

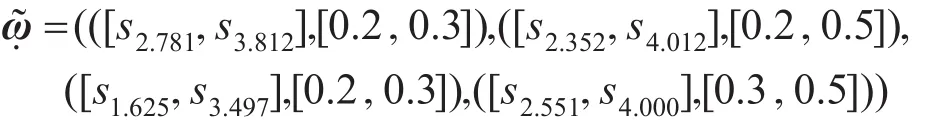
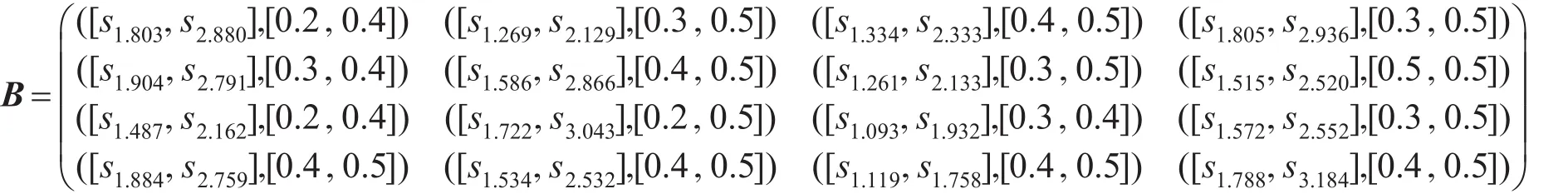
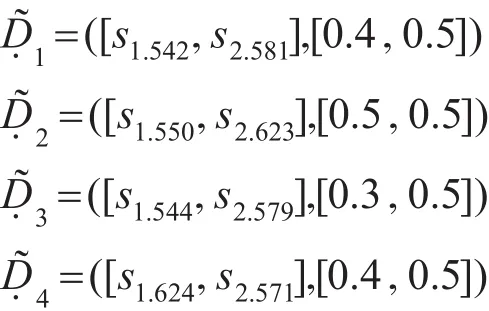
D1＝1.007，D2＝0.954，D3＝1.070，D4＝1.034从而得到4个移动银行服务质量优劣的排序c3≥c4≥c1≥c2，即c3为服务质量最优的移动银行。

5.2属性权重未知的情形

针对属性权重完全未知的情形，由式（1）、式（9）得到方案ci（i＝1，2，3，4）与其他所有方案关于属性uj（j＝1，2，3，4）的评价偏差所构成的矩阵为：

由式（10）可以得到所有属性的信息熵值分别为：

E1＝0.990，E2＝0.973，E3＝0.977，E4＝0.965

则由式（11）求得属性权重向量为：

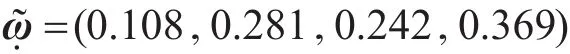
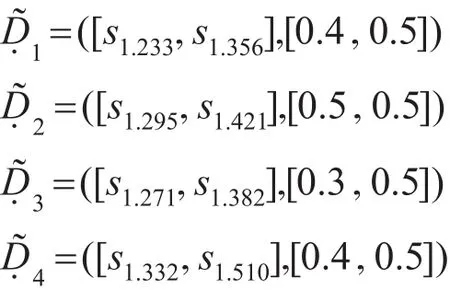
D1＝0.679，D2＝0.669，D3＝0.741，D4＝0.742

从而得到4个移动银行服务质量优劣的排序c4≥c3≥c1≥c2，即c4为服务质量最优的移动银行。

当属性权重由各决策者直接给出时，属性权重值与各决策者给出的评价信息无直接关系；而当属性权重完全未知时，采用信息熵法确定属性权重，即基于所有方案对某属性的评价偏差大小与该属性权重大小的一致性确定属性权重，所得属性权重值与各决策者给出的评价信息直接相关。因此，在属性权重已知或完全未知这两种不同的情形下，得到的移动银行服务质量优劣的排序结果存在一定的差异，这是完全正常的，在一定程度上体现了实际决策问题的模糊性与灰色性。

6　结束语

从客观事物的复杂性、不确定性及决策专家思维特点出发，实际决策问题兼具有模糊性与灰色性。基于不确定语言变量表达模糊信息的优势，本文针对属性权重已知或完全未知两种的不同情形，提出了一种属性值为区间灰色不确定语言变量的多属性群决策方法。采用IGULWGA算子及IGULHWGA算子集结评价信息，采用信息熵法确定未知的属性权重，给出了群决策方法及步骤，并用决策方法对移动银行服务质量进行了评估。本文方法丰富了已有的灰色模糊多属性群决策方法，为解决区间灰色不确定语言多属性群决策问题提供了良好的途径。

References:

[1] Jiang Yanping，Fan Zhiping，Ma Jian. A method for group decision making with multi-granularity linguistic assessment information[J]. Information Sciences，2004，178（4）: 1098-1109.

[2] Wei Guiwu. Uncertain linguistic hybrid geometric mean operator and its application to group decision making under uncertain linguistic environment[J]. International Journal of Uncertainty，Fuzziness and Knowledge-Based Systems，2009，17（2）: 251-267.

[3] Fan Zhiping，Liu Yang. A method for group decision making based on multi-granularity uncertain linguistic information[J]. Expert Systems with Applications，2010，37（5）: 4000-4008.

[4] Li Peng，Liu Sifeng. Interval-valued intuitionistic fuzzy numbers decision-making method based on grey incidence analysis and D-S theory of evidence[J]. Acta Automatica Sinica，2011，37（8）: 993-998.

[5] Han Erdong，Guo Peng，Zhao Jing. Group decision making method based on two-tuple linguistic with different forms of preference evaluation information[J]. Computer Engineering and Applications，2015，51（4）: 35-40.

[6] Dai Wenzhan，Li Jiuliang. Off-target deviation degree method for grey multi-attribute group decision making[J]. Systems Engineering Theory and Practice，2014，34（3）: 787-792.

[7] Lin S L，Lee P C，Chang T P. Practical expert diagnosis model based on the grey relational analysis technique[J]. Expert Systems with Applications，2009，36（2）: 1523-1528.

[8] Hamzaçebi C，Pekkaya M. Determining of stock investments with grey relational analysis[J]. Expert Systems with Applications，2011，38（8）: 9186-9195.

[9] Bu Guangzhi，Zhang Yuwen. Grey fuzzy comprehensive evaluation based on the theory of grey fuzzy relation[J]. Systems Engineering Theory and Practice，2002，22（4）: 141-144.

[10] Jin Na，Lou Shouchun. A grey fuzzy multi-attribute decision making method[J]. Fire Control Command Control，2004，29（4）: 26-28.

[11] Luo Dang，Liu Sifeng. Analytic method to a kind of grey fuzzy decision making based on entropy[J]. Engineering Science，2004，6（10）: 48-51.

[12] Zhu Shaoqiang，Meng Ke，Zhang Hengxi. Interval numbers grey fuzzy comprehensive evaluation and its application[J]. Electronics Optics and Control，2006，13（3）: 36-37.

[13] Wang Jianqiang，Wang Jun. Interval grey fuzzy multi-criteria decision making approach[J]. Systems Engineering and Electronics，2008，30（12）: 2409-2411.

[14] Liu Peide，Zhang Xin. Multi-attribute group decision making method based on interval grey linguistic variables weighted geometric aggregation operator[J]. Control and Decision，2011，26（5）: 743-747.

[15] Wei Guiwu. Grey relational analysis method for 2-tuple linguistic multiple attribute group decision making with incomplete weight information[J]. Expert Systems with Applications，2011，38（5）: 4824-4828.

[16] Cao Guo，Shen Lixiang. A multiple attribute group decision making model based on three-parameter interval grey linguistic variable[J]. Operations Research and Management Science，2014，23（1）: 66-73.

[17] Hu Lifang，Guan Xin，He You. A new approach for grey multi-attribute decision making[J]. Control and Decision，2012，27（6）: 895-898.

[18] Wang Huidong，Liu Peide，Li Chengdong，et al. A multiattribute group decision making method based on interval grey trapezoidal fuzzy numbers[J]. Journal of Inner Mongolia University: Natural Science Edition，2014，45（1）: 51-58.

[19] Han Erdong，Guo Peng，Zhao Jing. Method for uncertain linguistic group decision making based on projection and dominance degree[J]. Journal of Sichuan University: Engineering Science Edition，2015，47（1）: 143-149.

[20] Yager R R. OWAaggregation over a continuous interval argument with applications to decision making[J]. IEEE Transactions on Systems，Man，and Cybernetics: Part B Cybernetics，2004，34（5）: 1952-1963.

[21] Zhang Qiansheng，Jiang Shengyi. A note on information entropy measures for vague sets and its applications[J]. Information Sciences，2008，178（21）: 4184-4191.

[22] Boran F E，Genç S，Kurt M，et al. A multi-criteria intuitionistic fuzzy group decision making for supplier selection with TOPSIS method[J]. Expert Systems with Applications，2009，36（8）: 11363-11368.

附中文参考文献：

[4]李鹏，刘思峰.基于灰色关联分析和D-S证据理论的区间直觉模糊决策方法[J].自动化学报，2011，37（8）: 993-998.

[5]韩二东，郭鹏，赵静.二元语义处理不同偏好评价信息的群决策方法[J].计算机工程与应用，2015，51（4）: 35-40.

[6]戴文战，李久亮.灰色多属性偏离靶心距群决策方法[J].系统工程理论与实践，2014，34（3）: 787-792.

[9]卜广志，张宇文.基于灰色模糊关系的灰色模糊综合评判[J].系统工程理论与实践，2002，22（4）: 141-144.

[10]靳娜，娄寿春.一种灰色模糊多属性决策模型[J].火力与指挥控制，2004，29（4）: 26-28.

[11]罗党，刘思峰.一类灰色模糊决策问题的熵权分析方法[J].中国工程科学，2004，6（10）: 48-51.

[12]朱绍强，孟科，张恒喜.区间数灰色模糊综合评判及其应用[J].电光与控制，2006，13（3）: 36-37.

[13]王坚强，王君.一种区间灰色模糊多准则决策方法[J].系统工程与电子技术，2008，30（12）: 2409-2411.

[14]刘培德，张新.一种基于区间灰色语言变量几何加权集成算子的多属性群决策方法[J].控制与决策，2011，26（5）: 743-747.

[16]曹国，沈利香.一种基于三参数区间灰色语言变量的多属性群决策方法[J].运筹与管理，2014，23（1）: 66-73.

[17]胡丽芳，关欣，何友.一种新的灰色多属性决策方法[J].控制与决策，2012，27（6）: 895-898.

[18]王会东，刘培德，李成栋，等.一种基于区间灰色梯形模糊数的多属性群决策方法[J].内蒙古大学学报:自然科学版，2014，45（1）: 51-58.

[19]韩二东，郭鹏，赵静.基于投影及优势度的不确定语言群决策方法[J].四川大学学报:工程科学版，2015，47（1）: 143-149.

HAN Erdong was born in 1987. He is a Ph.D. candidate at School of Management，Northwestern Polytechnical University. His research interests include grey system theory，decision theory and method，etc.

韩二东（1987—），男，河南三门峡人，西北工业大学管理学院博士研究生，主要研究领域为灰色系统理论，决策理论与方法等。

GUO Peng was born in 1962. He is a professor and Ph.D. supervisor at School of Management，Northwestern Polytechnical University. His research interests include project risk management and decision support system，etc.

郭鹏（1962—），男，陕西西安人，西北工业大学管理学院教授、博士生导师，主要研究领域为项目风险管理，决策支持系统等。

ZHAO Jing was born in 1984. She is a lecturer at School of Management，Northwestern Polytechnical University. Her research interests include project decision making and evaluation，project risk measure and control，etc.

赵静（1984—），女，河南禹州人，西北工业大学管理学院讲师，主要研究领域为项目决策与评价，项目风险测度与控制等。

欢迎订阅2016年《计算机科学与探索》、《计算机工程与应用》杂志

《计算机科学与探索》为月刊，大16开，单价40元，全年12期总订价480元，邮发代号：82-560。

邮局汇款地址：

北京619信箱26分箱《计算机科学与探索》杂志社（收）邮编：100083

《计算机工程与应用》为半月刊，大16开，每月1日、15日出版，单价45元，全年24期总订价1080元，邮发代号：82-605。

邮局汇款地址：

北京619信箱26分箱《计算机工程与应用》杂志社（收）邮编：100083

欢迎到各地邮局或编辑部订阅。个人从编辑部直接订阅可享受8折优惠！

发行部

电话：（010）89055541

Method for Multi-Attribute Group Decision Making Based on Interval Grey Uncertain Linguistic Information*

HAN Erdong＋，GUO Peng，ZHAO Jing
School of Management，Northwestern Polytechnical University，Xi’an 710072，China
＋Corresponding author: E-mail: handong1987_2006@126.com

HAN Erdong，GUO Peng，ZHAO Jing. Method for multi-attribute group decision making based on interval grey uncertain linguistic information. Journal of Frontiers of Computer Science and Technology，2016，10（1）：93-102.

Abstract:With respect to multi-attribute group decision making problems，where the attribute values take the form of the interval grey uncertain linguistic variables，three kinds of geometric aggregation operators are given based on the definition and operation rules of interval grey uncertain linguistic variables. According to interval grey uncertain linguistic weighted geometric aggregation operator，evaluation matrices which are given by all decision makers are aggregated to the group evaluation matrix. In the case of known attribute weights information，attribute weights vectors which are given by every decision maker are aggregated to the group attribute weights vector; when the attribute weights are unknown completely，the attribute weights are determined based on information entropy method. All attribute values of alternatives are concentrated by interval grey uncertain linguistic hybrid weighted geometric aggregation operator，then comprehensive evaluation values of alternatives are received，the rank results of alternatives are obtained based on one comparison of the interval grey uncertain linguistic variables. Finally，an illustrative example analysis shows the effectiveness and feasibility of the proposed method.

文献标志码：A

中图分类号：C934

doi:10.3778/j.issn.1673-9418.1503033