基于马尔可夫决策过程的机会网络转发策略*
张 杨,王小明+,林亚光,张 丹
1.现代教学技术教育部重点实验室,西安710119
2.陕西师范大学计算机科学学院,西安710119
* The National Natural Science Foundation of China under Grant No. 61373083 (国家自然科学基金); the Fundamental Research Funds for the Central Universities of China under Grant No. GK201401002 (中央高校基本科研业务费专项资金); the Program of Science and Technology Innovation Team of Shaanxi Province under Grant No. 2014KTC-18 (陕西省重点科技创新团队项目).
Received 2015-04,Accepted 2015-08.
CNKI网络优先出版:2015-08-27, http://www.cnki.net/kcms/detail/11.5602.TP.20150827.1531.012.html
ISSN 1673-9418 CODEN JKYTA8
Journal of Frontiers of Computer Science and Technology
1673-9418/2016/10(01)-0082-11
基于马尔可夫决策过程的机会网络转发策略*
张杨1,2,王小明1,2+,林亚光1,2,张丹1,2
1.现代教学技术教育部重点实验室,西安710119
2.陕西师范大学计算机科学学院,西安710119
* The National Natural Science Foundation of China under Grant No. 61373083 (国家自然科学基金); the Fundamental Research Funds for the Central Universities of China under Grant No. GK201401002 (中央高校基本科研业务费专项资金); the Program of Science and Technology Innovation Team of Shaanxi Province under Grant No. 2014KTC-18 (陕西省重点科技创新团队项目).
Received 2015-04,Accepted 2015-08.
CNKI网络优先出版:2015-08-27, http://www.cnki.net/kcms/detail/11.5602.TP.20150827.1531.012.html
ISSN 1673-9418 CODEN JKYTA8
Journal of Frontiers of Computer Science and Technology
1673-9418/2016/10(01)-0082-11
E-mail: fcst@vip.163.com
http://www.ceaj.org
Tel: +86-10-89056056
摘要:在机会网络节点随机移动的场景中,提高路由算法性能评价中的投递率,控制开销率,降低平均迟延是持续的研究方向。由于目前机会网络结构稀疏和拓扑多变,单副本路由转发策略效率较低。通过结合花粉布朗运动与机会网络节点的随机运动的相似性,并分析节点随机运动的规律,定义了一种基于马尔可夫决策过程的节点转发策略。该策略在平均延时适当增加的情况下,可以有效控制网络开销率,提高消息投递率。最后通过仿真实验验证了理论模型的正确性。
关键词:机会网络;马尔可夫决策;投递率
1 引言
机会网络[1-2](opportunistic network)源于容忍延迟网络[3](delay tolerant networks,DTN)和移动自组网[4](mobile ad-hoc networking,MANET),可以视为是两者的子类。机会网络是一种不需要在源节点和目的节点之间存在完整路径,利用节点移动带来的相遇机会实现网络通信,时延和分裂可容忍的自组织网络[5]。
在机会网络路由节点转发算法评价分析中,需要关心3个参数[6]:(1)递交率,目的节点成功接收到的报文与所有目的节点接收的报文个数之间的比值;(2)平均迟延,被成功递交的报文从源节点到达目的节点所耗费的时间总和与递交报文个数之比;(3)开销率,成功递交的数据包被中继的次数与被成功递交的数据包个数之差再除以被成功递交的数据包的个数。一个有效的节点转发策略需要考虑3个参数之间的约束以达到最佳期望[4,7-8]。
单副本[9-11]的路由策略是同一时间内网络中只保留消息的一个副本。现有几种基于单副本的机会网络节点转发策略:(1)First Contact[12],该算法源节点将数据分组转发给它遇到的第一个节点;(2)Direct Delivery[13],该算法源节点仅在遇到目标节点时才将数据分组转发给下一节点;(3)随机路由[14]以概率P将消息发送给其遇到的节点;(4)Seek and Focus[11]结合了随机路由和基于效用路由的转发策略;(5)Simbet[15]中节点只将数据分组转发给具备一定相似度的节点。
在某些随机网络场景中,如地震、海啸等灾难后短期缺乏充电条件的情况下,幸存者之间用智能手机组成一个随机网络传递各种救援消息。考虑到网络节点设备的电源有限,需要节省网络中的开销率,同时提高消息对目标节点的投递率。结合随机网络中节点随机运动,并且在单副本的情况下,在有效保持源节点对目的节点的投递率的同时,控制一定的开销率使平均延迟最小,即找出一种机会网络节点的转发策略,使该策略的评价参数以此方式达到最优平衡。
本文机会网络中的节点在规定区域内的随机移动类似于花粉的布朗运动[16]。对布朗运动的数学描述是维纳过程[17],而维纳过程具有马尔可夫性质[18]。马尔可夫决策过程[19](Markov decision processes,MDP)根据每个时刻观察到的状态,从可用的行动集合中选用一个行动作出决策,系统下一步的状态是随机的,并且其状态转移概率具有马尔可夫性。本文利用机会网络随机过程的马尔可夫性寻找符合课题要求的单副本节点转发策略。
本文研究了机会网络单副本情况下现有的两种转发策略:First Contact和Direct Delivery。在此基础上,分析了另外两种已有单副本路由Seek and Focus 和Simbet。针对机会网络3种路由评价分析参数,进行了如下研究:
(1)找出了一种机会网络中基于马尔可夫决策过程的节点转发状态转移规律,并且遵循规律推算出与此相关的参数平衡收益;
(2)根据上述规律提出了一种节点转发策略,该策略可以在一定的平均时延下,用有限的开销率使节点投递率最大化;
(3)通过实验对比了多组本文所提策略相关参数和经典单副本路由,用仿真实验验证了模型和理论的正确性。
2 相关工作
现有机会路由按选择广播节点的方式可分为两类[20-22]:第一类算法根据链路统计信息为每个节点赋予一个全局度量值,又称优先级或梯度,数据总是从低优先级的节点向高优先级的节点传输,而目的节点具有最高的优先级,从而保证传输方向正确;第二类算法为每个节点指定一组可能的下一跳节点集合,又称转发集合或候选集合,该类算法通过避免环路以保证传输方向正确。这两类算法都借鉴了传统无线路由的转发机制,每个广播节点将数据包成功转发后不会再次参与广播,下一跳节点从刚接收到数据包的节点中选择。
First Contact路由[9-10,12],在理论上不考虑丢包和延时的情况下,对目标节点的投递概率为f1=1/n,开销率最大。但是在实际情况中,该算法通过节点多次相遇转发完成投递,因为最先遇到的节点是未知的,所以该策略具有一定的盲目性,在大范围的随机场景中投递率不高。
Direct Delivery路由[9-10,13],理论上对目标节点的投递概率f2=1,但是平均延时最大;实际情况中,每个消息只传输一次,从而总的传输次数最少,但是在间歇连接的网络中,由于链路的可靠性不能保障,从而导致投递率低,平均迟延高。
P路由[11,14],对于任意非目的节点,会以一定概率P(P>0)将本节点所持有的消息传递给对方,其投递率与P有关。在没有任何先验知识的情况下,无法选择一个符合网络最优情况的概率P。
Seek and Focus路由[9-11],这是一个混合策略,此路由存在一个二维策略函数F(P,S),P为节点转发概率,S为节点效用值的阀值。当遇到随机节点n时,如果当前节点效用值低于阀值,则执行随机概率转发;如果当前节点效用值大于阀值,则执行基于效用的转发。节点的效用值根据两类路由基础算法在不同的场景中存在不同的定义方法。SF路由实际上是P路由的改进版本。同样在没有任何先验知识的情况下,无法选择合适的转发概率P和阀值S,应该在具体场景中以实验来验证。
Simbet路由[9,15],该策略以社会网络的思想确定相遇节点的相似度判断是否转发消息。而节点相似度的判断标准是根据第一类路由算法为每个节点赋予一个全局度量值,即节点等级。节点的相似度有运动相似度和节点社会属性相似度等。
文献[19]提到马氏决策过程的定义,系统地分析了其理论框架并给出了有效的算法。除此之外,该文献定义了有现阶段马尔可夫决策过程的五重组:
{T,S,A(i),P(⋅|i,α),R(i,α)}
其中,T为离散时间决策阶段;S为系统所有可能状态,在每个决策时刻,对系统的描述就是状态,S也称为状态空间。如果在任一个决策时刻,决策者观察到的状态是i∈S,他可以在状态i的可用行动集A(i)中选取行动α,其中A(i)也称为行动空间,并且假定S 和A(i)都不依赖于时刻T,除非特别声明,总考虑S和A(i)都是离散的情况。任意一个决策时刻,在状态i采取行动α∈A(i)后,有两个结果:(1)决策获得报酬R(i,α);(2)下一个决策时刻系统所处的状态由概率分布P(⋅|i,α)决定。R(i,α)是定义在i∈S和α∈A(i)上的实值函数。当R(i,α)为正值时,表示收入;当其为负值时,表示费用。从模型的角度来看,报酬R(i,α)是即时的。通常情况下报酬还依赖下一个决策时刻的状态j,即R(i,α,j),那么行动α的期望值报酬为:
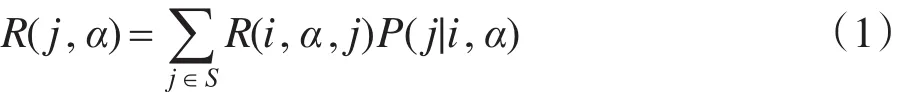
非负函数P(j|i,α)是下一个决策时刻系统转移到状态j的概率。函数P(j|i,α)被称为转移概率函数。根据马氏状态转移矩阵性质,通常假设:

文献[11]分析了主流单副本机会网络路由,并且提出了基于马尔可夫链的节点概率转发策略。文献[23]分析了校园环境下学生所携带移动节点的运动特点,采用半马尔可夫过程模拟节点运动并建立了相应的DTN节点移动模型,对模型进行了仿真和分析,将仿真结果与随机路径点(random way point,RWP[24])模型及实际路径信息进行对比,可以看出半马尔可夫过程模型能够更准确地描述实际网络环境。文献[25]中的算法具有学习功能,能够解决复杂的容迟容断网络环境中的高延迟和频繁割裂问题。文献[26]提出了基于网络拓扑图的马氏链模型,为多副本的节点转发策略找到了基于马氏链的预测投递机制。
现有关于应用马尔可夫决策过程的文献很多都是研究多副本情况下的机会网络转发策略。因此本文结合机会节点移动的特点,利用马尔可夫决策过程构建机会网络节点转发策略,研究和对比分析单副本情况下的投递率、开销率与平均时延之间的平衡关系。
3 机会网络节点转发策略
首先建立一个完全随机的机会网络模型,该随机模型完全符合马尔可夫决策过程。然后静态定义网络中节点的优先级,建立基于马尔可夫决策过程的节点转发策略模型。该策略的思想是,在节点遇到前[N/e]个节点中,如果遇到目的节点则直接递交消息;如果没有遇到目的节点,则递交于下一个遇到的且当前优先级最高的节点。
3.1场景描述
如图1所示,在一个地形随机的区域中,存在不同优先级梯度的节点N个,按照第一类基础路由算法定义源节点S,目的节点D,场景中有N个节点。假定从源节点转发消息到目的节点,按照优先级梯度,S的优先级最小,D最大。从低优先级的节点向高优先级的节点传输,根据遇见节点的优先级梯度来判断消息转发与否。考虑到场景中源节点携带消息按照随机方式运动,途中遇见的任意节点也是随机的,符合离散时间有限阶段马尔可夫决策过程。
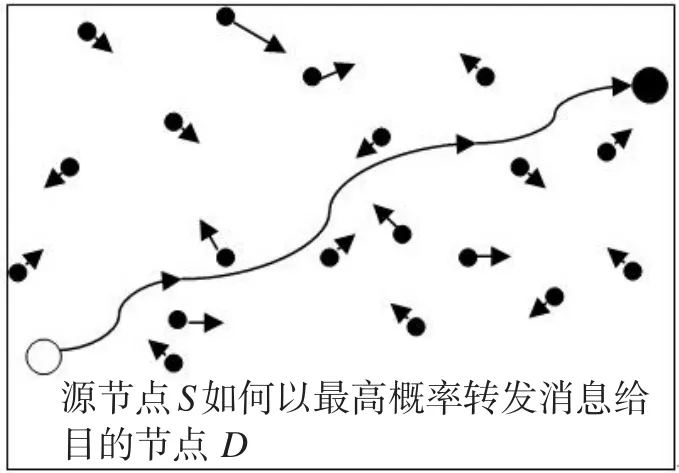
Fig.1 Stochastic model of opportunistic network图1 机会网络随机场景
3.2转发策略
本文不考虑计算节点的优先级,直接定义节点的优先级排序,把源节点S定义为Lv0,把目的节点D定义为Lv(N−1):
Lv0<Lv1<Lv2<…<Lv(N−1)
该策略是找到源节点携带消息出发,遇见高优先级的节点然后转发消息,重复路由策略直到目的节点收到消息过程结束。节点按照随机方式移动,定义基于马尔可夫决策过程的节点转发策略模型。
当源节点随机遇见某一个节点时,需要判断高优先级节点后决定消息是否转发,这里设定从阶段1开始到阶段N时结束,因此决策的阶段数与节点数目相同,即有N个不同优先度的节点,就会有T个决策时刻。定义马尔可夫决策过程状态空间S′={0,1}。状态空间S′有两个元素0和1。其中1代表当前的节点是目的节点;0表示当前的节点不是目的节点。
对于每一个状态定义行动集A(0)=A(1)={X,Y},行动Y表示传送消息给当前节点,行动X表示跳过当前节点,并准备相遇下一个节点。根据机会路由投递消息的要求,除了在全部过程停止时,所有其他时间阶段的报酬都是0,也就是在选取行动X(放弃当前的节点)时的报酬总是0。反之,只有当采取行动Y的时刻系统具备有效报酬。有效报酬的概念表示选中的节点是目标节点的概率,它是这样确定的:
P(D)=P{目的节点在前n个相遇节点中}

定义报酬值:

另外,为了描述过程的结束情况,用Ø表示过程的停止状态。根据马尔可夫性质,转移概率是不依赖于当前状态i的,而且只要采取行动X,过程就会继续下去。
定义转移概率,在时刻t+1,恰好在前n+1个节点中遇到目的节点的概率是:

根据式(2),则未遇到目的节点的概率是:

图2为路由模型的状态转移图。对于i=0,1,得出马氏决策过程的五元组:
{T,S,A(i),Pt(j|i,α),Rt(i,α)}
决策时刻T={1,2,…,N},N<∞
可能的状态S=S′∪{Ø}={0,1,Ø}
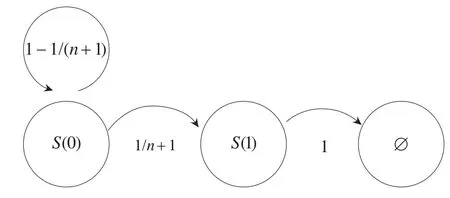
Fig.2 State transition diagram图2 状态转移图
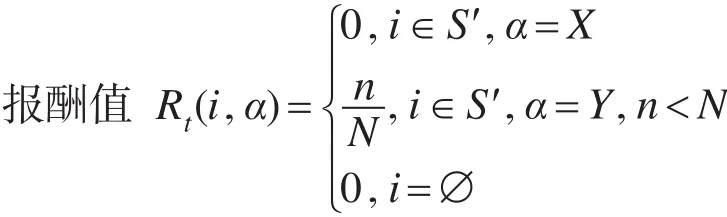
则转移概率为:
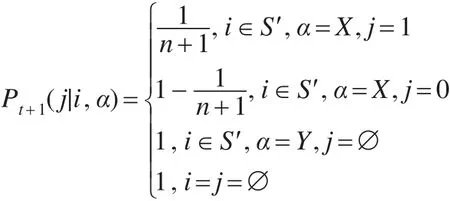
这里就定义好了解决这个节点转发策略的马氏决策过程数学模型。下面给出求解过程。用Ut(1)表示从当前时段到过程结束源节点能够遇到目标节点的最大概率;用Ut(0)表示在剩下时段中源节点能够遇见目的节点的最大概率,而此时遇见的节点不是目标节点。那么,它们满足下面的关系:
对于n=1,2,…,N−1,有:
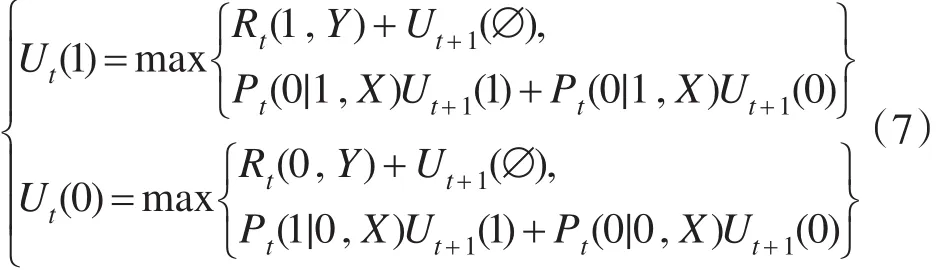
考虑到Ut+1(Ø)=Ut(Ø)=0,Ut≥0,化简:
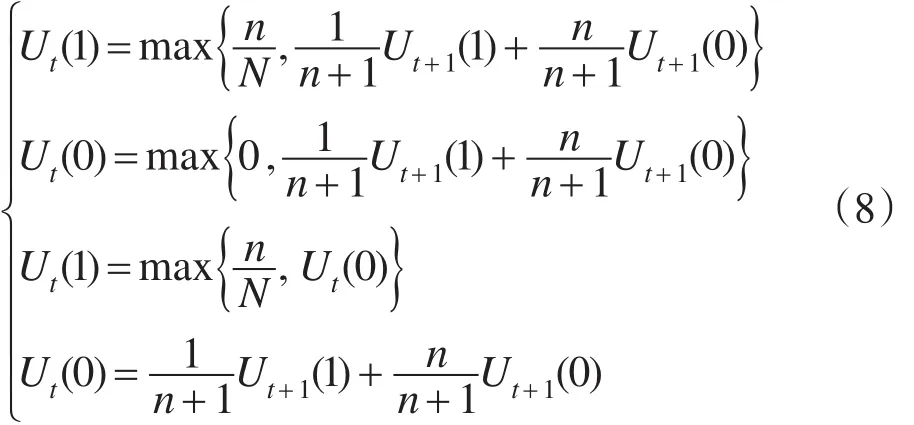
从上式分析得出,最优策略具有这样的结构:t时刻如果在状态S(1),有Ut(0)<n/N,最优行动是停止并且传递消息;如果Ut(0)>n/N,最优行动就是继续寻找下一节点;如果Ut(0)=n/N,两者都是最优行动。在状态S(0),继续下去是最优的选择。
当节点数目N确定以后,此机会网络节点转发策略是先观察K个候选节点,然后比较并记录其中最好的节点Lv(a),在放弃前K个节点后,选择第一个优于Lv(a)的节点Lv(b),其中b>a。下面给出求解K的过程:
把1到N个节点按照优先级进行排列共有N!种可能。对于某个固定的K,如果目的节点出现在第M个位置(K<M≤N),且从K+1到M−1位置的节点优先级小于前K位置中的最优节点,就必须得满足前M−1个节点中的最优节点在前K个节点里,这有K/(M−1)的可能。得到计算目的节点被选中的概率公式P(K):
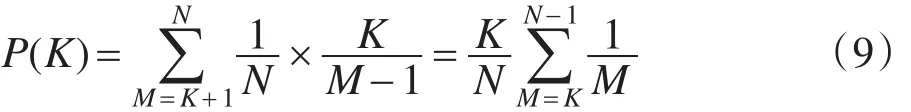
用x来表示K/N的值,x=K/N,K=Nx,确定积分上界N−1,积分下界M=K=Nx,假设N充分大,N−1≈N,则上述公式可以改写成:
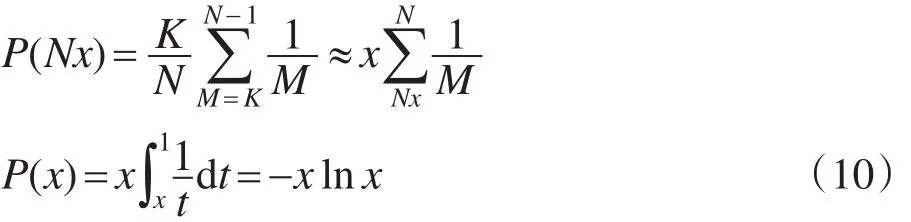
为了求出K和P(K)的极值,对上式求导,并令这个导数为0。
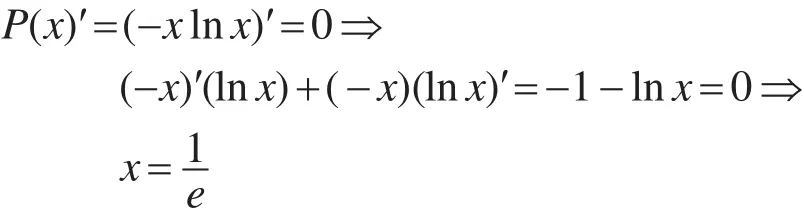
因为x=K/N且K是自然数,所以结果取整得到:

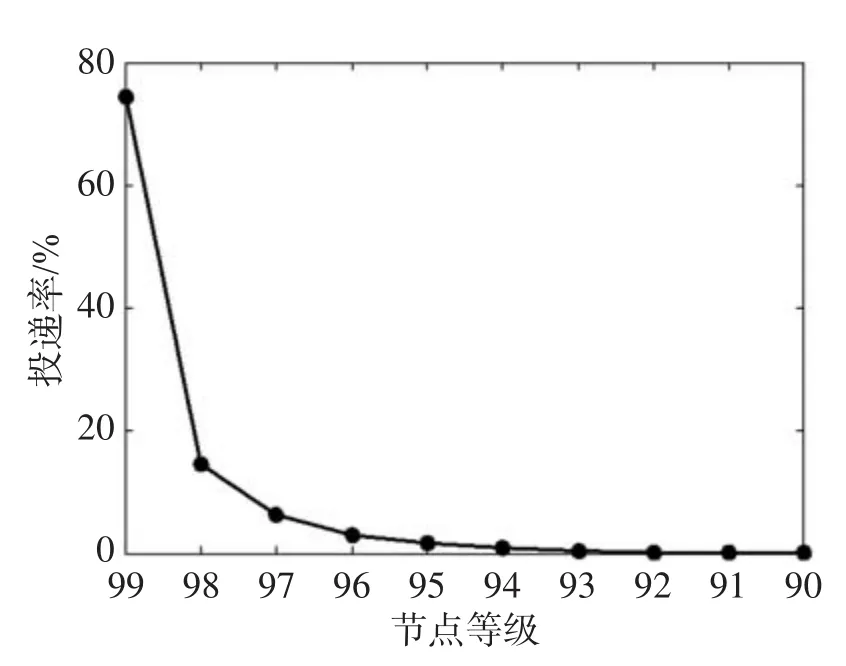
该机会网络转发策略的核心思想是记录源节点遇见的前[N/e]个节点,如果遇见目的节点则直接递交消息,如果前[N/e]个节点不是目的节点,记录其中最高优先度节点的Lv(a)值并放弃前[N/e]个节点,之后选择剩下的N−[N/e]中的任何一个优于Lv(a)的节点传递消息,并继续寻找目的节点D,直到消息传递完毕为止。此转发策略使源节点对目的节点的跳数最小值为1。
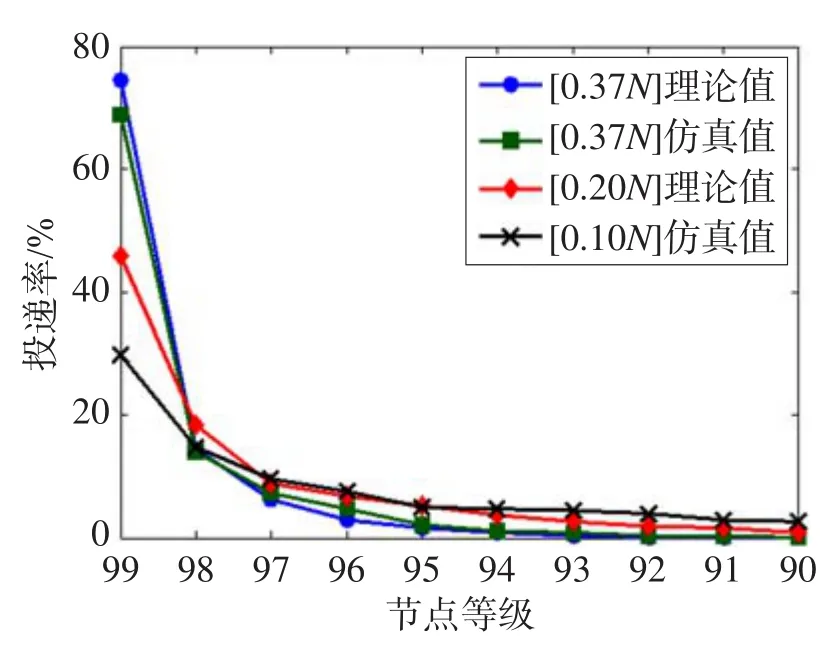
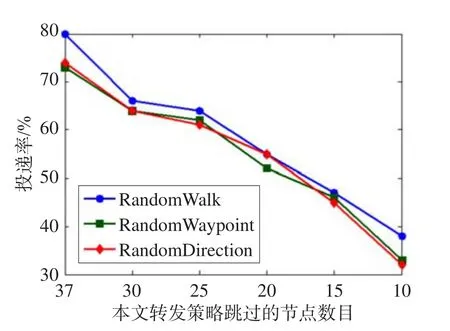
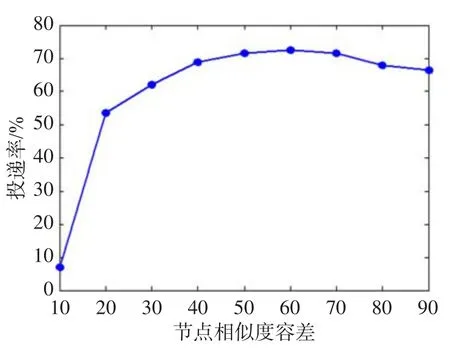
对于任意节点i的转发策略代码如下所示:
1. Begin
2. if (contact Node i)
3. //源节点相遇节点i
4. if (i=Message’s target)
5. transfer Message to Node i;
6. //如果节点i是目标节点,则转发消息
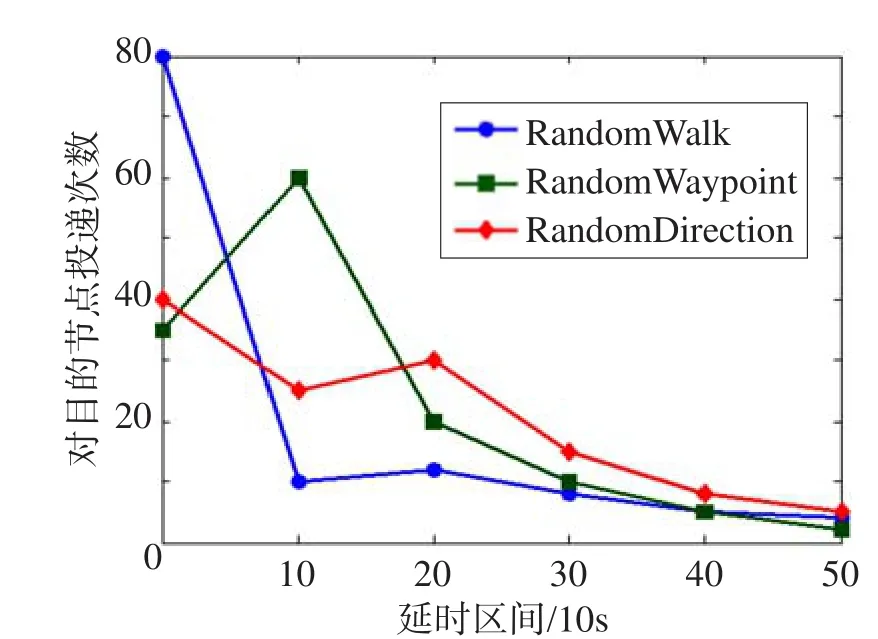
7.else if ([N/e].length 8.add i to [N/e]; 9. //判断是否是前[N/e]的节点 10. else if (i>[N/e].Max) 11. transfer Message to Node i; 12. //选择剩下的N−[N/e]中的任何一个优于Lv(a)的节点传递消息 13.else 14.return; 15.End if 16.End if 17. End if 18.End if 19.End 整个算法理论上源节点对目的节点的投递率最大值为: 源节点相对于其他等级节点的投递率按照递推公式计算: 4.1数值实验 算法数值实验采用Matlab编程计算,设节点数N=100,按节点等级区分,0号节点是源节点,99号节点是目的节点,根据递推公式(12),可以计算出本文转发策略下对应不同等级节点的投递率,如图3所示。 Fig.3 Statistical result of numerical experiment图3 数值实验统计结果 本文的转发策略是K1=[N/e],取整后等于[0.37N],即略过前37个节点后转发给第一个比之前遇到所有节点等级都高的节点。 4.2仿真实验 本文采用ONE仿真平台[27]评估转发策略。利用ONE仿真平台可以有效地模拟真实情况下节点的活动与相遇情况。 仿真实验中进行了随机运动模式实验,模拟场景大小为1 000 m×1 000 m,节点个数为100,平均移动速度为10 m/s,接口带宽为250 Kb/s,接口范围为10 m,仿真次数200次取平均值,消息大小为50 KB。采用3种不同的随机移动模型:随机路点RandomWaypoint,随机方向RandomDirection,随机漫步RandomWalk。 4.2.1投递率 通过前面的数学计算,了解到在一个随机场景中,源节点跳过先前遇到的37个节点会使对目的节点的投递率最大化。第一组实验是为了对比本文转发策略其他阀值的效果,即可以选取跳过的节点数。这里取了另一组经验参数K2=[0.20N],即跳过前20个节点。选取这个参数的依据来源于邓巴定律[28],文献中提到无论你曾经认识多少人,或者通过一种社会性网络服务与多少人建立了弱链接,那些强链接仍然在此次此刻符合“二八”法则[29],即在机会网络中随机遇到的20%的节点里面包含着目标节点的可能性是80%。第三组参数采取随机经验参数K3=[0.10N]。实验仿真的数据来源于3种随机运动模式下节点投递率的平均值。 如图4所示,通过统计节点投递率,对比另外两组经验参数,本文转发策略在提高对目的节点的投递率方面有着非常明显的效果,但是对其他相似的非目的节点并无明显优势。同时也验证了理论计算出来的消息转发概率规律。 Fig.4 Delivery rates parameter experiment results analysis of forwarding strategy图4 转发策略参数实验投递率结果分析 如图5所示,第二组投递率实验在第一组内部参数的基础上对比了3种随机运动模式。由实验统计发现,自由漫步这种随机运动模式取得的投递率最高,说明节点运动模式越随机,则越符合本文提到的马尔可夫决策过程的相关规律。图中横坐标“转发策略跳过的节点数目”为本文所提策略的阀值。通过对比不同阀值观察投递率的变化。 Fig.5 Delivery rates of motion models on ONE simulation platform图5 ONE仿真平台上移动模型投递率实验 第三组投递率实验在随机运动模式的情况下,引入另外两种单副本路由策略作为比较。依据文献[11]提到的路由策略算法,仿真了Seek and Focus(SF)和Simbet在本文实验设计中的实际投递率。从图6和图7中发现,SF路由在不同转发概率和不同阀值的情况下,投递率围绕着一个数学期望呈现随机分布的特性。在第三组实验中SF路由取其投递率均值作为对比。Simbet的仿真实验用了节点相似度容差作为观察参数,节点相似度容差越小则节点越相似,容差越大则说明节点相似度差异就越大。在仿真实验中其路由投递率随着不同节点相似度容差的递增而增加,在本组实验中,取其最优值进行实验对比。通过实验观察,本文策略在3种节点随机移动模型中投递率差异较小。 Fig.6 Simert delivery rates analysis图6 Simbert投递率分析 Fig.7 SF delivery rates analysis图7 SF投递率分析 图8统计了本文路由策略和另外3组路由策略Direct Delivery(DD)、Seek and Focus(SF)、Simbet在不同随机运动模型下的投递率,通过200次实验取其平均值,可以发现在随机漫步的运动模型下,本文策略的投递率略高于DD路由、SF路由和Simbet路由,说明越随机的行为模式越符合马尔可夫决策过程的规律。同时发现一个现象,就是在随机路点模型下,Simbet路由的投递率上升。这是因为随机路点运动模型下,节点的运动规律趋于中心化,这符合节点运动的社会属性的规律,从而基于节点相似度的单副本路由Simbet的优势就体现出来。 Fig.8 Delivery rates of different routing strategies on ONE simulation platform图8 ONE仿真平台上不同路由策略投递率实验 4.2.2开销率 第一组实验对比了本文转发策略3个参数在3种随机运动模型下的开销率:成功递交的数据包被中继的次数与被成功递交的数据包个数之差再除以被成功递交的数据包的个数。从表1中可以发现,自由漫步运动模式有着稍好的表现。说明节点运动模式越随机,则越符合本文提到的马尔可夫决策过程的相关规律,具体表现为网络中的数据包成功递交的次数越多,而被中继的次数越少,网络负载越低,效率越优秀。 第二组开销率实验统计了本文路由策略和另外3组路由策略Seek and Focus(在相同实验场景设计中,取不同的转发概率P和不同阀值S后的开销率平均值)、Simbet(在相同实验场景设计中,取不同的节点相似度容差后的开销率平均值)以及有着最优开销率的Direct Delivery在3种随机运动模型下的开销率。通过200次实验取平均值,从表2中可以发现,在3种随机运动模型下各种路由的开销率差异不大,但是自由漫步模式总体最优。本文转发策略和Direct Delivery因为每次节点传递消息中介次数只有一次,所以开销率明显低于Seek and Focus和Simbet路由,同时本文转发策略因为规避一定数量的相遇节点,所以比盲目寻找目的节点的Direct Delivery路由的实际投递率高。开销率与递交成功的数据包有直接关系,这也造成了本文路由的开销率低于DD路由的实际结果。另外Simbet路由在随机路点移动模型中发挥了其社会属性的优势,节省了开销率。 4.2.3平均迟延 除此之外,需要研究实际情况中节点的延时情况,如图9和图10所示。 Table 1 Overhead rates of different motion models on ONE simulation platform表1 ONE仿真平台上不同运动模型开销率实验 Table 2 Overhead rates of different routing strategies on ONE simulation platform表2 ONE仿真平台上不同路由策略开销率实验 可以看出,本文转发策略在延时方面是有不足的,但是处于可以接受的范围内。图10中的延时是在略过37个节点的情况下与其他算法比较的,此时差于Simbet算法,但是依然远远优于Seek and Focus算法和Direct Delivery算法。从图9中可以看出,经验参数0.20N的延时要比0.37N的延时短,而0.10N有着最小的延时,也就是说略过前37个节点这个转发策略需要消耗一定的时间。因此本文的高投递概率是以牺牲一定延时为代价的,略过的节点越多,延时更大,但是递交率越高。 Fig.9 Statistical average delay of different motion models on ONE simulation platform图9 ONE仿真平台上不同运动模型平均延时统计 Fig.10 Statistical average delay of different routing strategies on ONE simulation platform图10 ONE仿真平台上不同路由策略平均延时统计 从图5、图9和表2中还可以发现,平均延时随略过节点数目增加而增加的趋势,略小于投递率随略过节点数目增加而增加的趋势,而远远小于网络负载随略过节点数目增加而减少的趋势。前两种变化呈现正比例的关系,而后者呈现指数关系。这是因为马氏决策过程在略过一部分节点后投递次数更少,网络负载更低,且递交率更为准确。这也验证了本文的理论,在略过一部分节点后,基于马氏决策过程的路由选择策略使得网络综合效率更高。因此,在对投递率要求较高的场景中,通过马氏决策过程适当略过一部分节点则对网络性能有很大的提升,根据实验结果认为37%为较好的选择。而在一般场景中,可以适当选取较少的略过节点的数量参数,在递交率和延时之间平衡折中,保证较高递交率和较低网络负载的同时也有着较短的消息延时,提高网络的整体通信效率,根据实验结果认为20%为较折中的选择。 为了更好地研究本文策略,设横轴为延时区间,纵轴为对目的节点投递次数,对比3种节点运动模式,如图11所示。 Fig.11 Statistical average delay on ONE simulation platform图11 ONE仿真平台上平均延时统计 可以发现RandomWalk在很快的时间内完成了绝大部分针对目的节点投递次数,从节省时间的情况上看是最为理想的,间接地验证了马尔可夫决策过程规律时间方面与空间方面的相似性。 机会网络是一种不需要源节点和目的节点之间存在完整链路,利用节点移动带来的相遇机会实现通信的自组织网络。 在随机的机会网络场景中,平衡3个机会网络的评价参数是一直研究的方向。本文结合了花粉布朗运动的数学含义与机会网络节点的随机运动特性,分析了节点随机运动的规律,定义了基于马尔可夫决策过程的一种节点转发策略,并研究了此策略下机会网络的参数平衡关系。通过理论模型分析和实验验证,本文提出的机会网络节点转发策略可以有效控制源节点对目的节点的开销率,并且保证其对目的节点的较高投递率,而不足之处是会增加平均延时。可以根据实际情况,向下调整转发策略参数,以求得更好的网络性能。 References: [1] Nguyen H A, Giordano S. Context information prediction for social-based routing in opportunistic networks[J]. Ad Hoc Networks, 2012, 10(8): 1557-1569. [2] Lin Yaguang, Wang Xiaoming, Zhang Lichen, et al. The impact of node velocity diversity on mobile opportunistic network performance[J]. Journal of Network and Computer Applications, 2015, 55: 47-58. [3] Casteigts A, Flocchini P, Mans B, et al. Measuring temporal lags in delay-tolerant networks[J]. IEEE Transactions on Computers, 2014, 63(2): 397-410. [4] Jeong J, Lee K, Yi Y, et al. ExMin: a routing metric for novel opportunity gain in delay tolerant networks[J]. Computer Networks, 2014, 59: 184-196. [5] Jiao Xianlong, Wang Xiaodong, Zhou Xingming. An efficient routing protocol in wireless ad hoc networks[J]. Journal of Frontiers of Computer Science and Technology, 2008, 2(5): 478-486. [6] Soares V N G J, Rodrigues J J P C, Farahmand F. GeoSpray: a geographic routing protocol for vehicular delay-tolerant networks[J]. Information Fusion, 2014, 15: 102-113. [7] Jang I, Choi W, Lim H. An opportunistic forwarding protocol with relay acknowledgment for vehicular ad hoc networks[J]. Wireless Communications and Mobile Computing, 2011, 11 (7): 939-953. [8] Shin W Y, Chung S Y, Lee Y H. Parallel opportunistic routing in wireless networks[J]. IEEE Transactions on Information Theory, 2013, 59(10): 6290-6300. [9] Conan V, Leguay J, Friedman T. Fixedpoint opportunistic routing in delay tolerant networks[J]. IEEE Journal on Selected Areas in Communications, 2008, 26(5): 773-782. [10] Liu Haitao, Zhang Baoxian, Mouftah H, et al. Opportunistic routing for wireless ad hoc and sensor networks: present and future directions[J]. IEEE Communications Magazine, 2009, 47(12): 103-109. [11] Spyropoulos T, Psounis K, Raghavendra C S. Efficient routing in intermittently connected mobile networks: the single-copy case[J]. IEEE/ACM Transactions on Networking, 2008, 16 (1): 63-76. [12] Amantea G, Rivano H, Goldman A. A delay-tolerant network routing algorithm based on column generation[C]//Proceedings of the 12th IEEE International Symposium on Network Computing and Applications, Cambridge, USA, Aug 2013. Piscataway, USA: IEEE, 2013: 89-96. [13] Lu Xiaofeng, Pan Hui, Lio P. High delivery performance opportunistic routing scheme for delay tolerant networks[J]. China Communications, 2012, 9(6): 145-153. [14] Daraghmi YA, Yi C W, Stojmenovic I. Forwarding methods in data dissemination and routing protocols for vehicular ad hoc networks[J]. IEEE Network, 2013, 27(6): 74-79. [15] Shin K, Lee D. Fame-based probabilistic routing for delaytolerant networks[J]. IEICE Transactions on Communications, 2010, E93-B(6): 1451-1458. [16] Shen Guangjun, Yan Litan. An approximation of subfractional Brownian motion[J]. Communications in Statistics: Theory and Methods, 2014, 43(9): 1873-1886. [17] Bahram A. Convergence of the increment of a wiener process[J]. Acta Mathematica Universitatis Comenianae, 2014, 83(1) : 113-118. [18] Dombry C, Eyi-Minko F. Stationary max-stable processes with the Markov property[J]. Stochastic Processes and Their Applications, 2014, 124(6): 2266-2279. [19] Niyato D, Wang Ping. Optimization of the mobile router and traffic sources in vehicular delay-tolerant network[J]. IEEE Transactions on Vehicular Technology, 2009, 58(9): 5095-5104. [20] Singh M P, Deen A J, Shukla P K. A comprehensive survey of routing strategies for vehicular ad-hoc networks[J]. Wireless Communication, 2013, 5(8): 328-333. [21] Spyropoulos T, Picu A. Opportunistic routing[M]//Mobile Ad Hoc Networking: the Cutting Edge Directions. 2nd ed. [S.l.]:Wiley-IEEE Press, 2013: 419-452. [22] Xiao Mingjun, Wu Jie, Liu Cong, et al. TOUR: time-sensitive opportunistic utility-based routing in delay tolerant networks[C]//Proceedings of the 32nd IEEE International Conference on Computer Communications, Turin, Italy,Apr 14-19, 2013. Piscataway, USA: IEEE, 2013: 2085-2091. [23] Guo Hang, Wang Xingwei, Huang Min, et al. Mobility modelof DTN nodes based on semi-Markov process[J]. Journal of Chinese Computer Systems, 2011, 32(7): 1273-1276. [24] Rhee I, Shin M, Hong S, et al. On the Levy-walk nature of human mobility[J]. IEEE/ACM Transactions on Networking, 2011, 19(3): 630-643. [25] Zhang Wenzhu, Sun Fayong, Wang Xuan. Study of the DTN routing algorithm based on the Markov decision[J]. Journal of Xidian University: Natural Science Edition, 2011, 38(2): 18-22. [26] Zhu Hao, Zhang Yu, Bai Shiyu. Evaluation method for node importance in networks based on Markov chain[J]. Journal of Circuits and Systems, 2013, 18(2): 452-456. [27] Pan Daru, Sun Jiajia, Liu Xiong, et al.Acampus based mobility model for opportunistic network[C]//Proceedings of the 2nd International Conference on Communications, Signal Processing, and Systems. [S.l.]:Springer International Publishing, 2014: 1039-1046. [28] Gonçalves B, Perra N, Vespignani A. Modeling users’activity on twitter networks: validation of dunbar’s number[J]. PloS One, 2011, 6(8): e22656. [29] Zhang Hangqing. Topological analysis of SNS social networks[D]. Shanghai: Donghua University, 2011. 附中文参考文献: [5]焦贤龙,王晓东,周兴铭.无线自组网中一种高效的路由协议[J].计算机科学与探索, 2008, 2(5): 478-486. [23]郭航,王兴伟,黄敏,等.基于半马尔可夫过程的DTN节点移动模型[J].小型微型计算机系统, 2011, 32(7): 1273-1276. [25]张文柱,孙发勇,王炫.基于马尔科夫决策的容迟网络路由算法[J].西安电子科技大学学报:自然科学版, 2011, 38 (2): 18-22. [26]朱浩,张玉,柏诗玉.基于马氏链的网络节点重要性评价方法[J].电路与系统学报, 2013, 18(2): 452-456. [29]张瀚青.基于SNS社交网络的模型及其拓扑分析[D].上海:东华大学, 2011. ZHANG Yang was born in 1984. He is a Ph.D. candidate at School of Computer Science, Shaanxi Normal University. His research interests include opportunistic network and social network, etc. 张杨(1984—),男,安徽阜阳人,陕西师范大学计算机科学学院博士研究生,主要研究领域为机会网络,社会网络等。 WANG Xiaoming was born in 1964. He received the Ph.D. degree from Northwest University in 2005. Now he is a professor and Ph.D. supervisor at School of Computer Science, Shaanxi Normal University, and the senior member of CCF. His research interests include wireless sensor network, mobile ad hoc networks, pervasive computing and social computing, etc. He has published more than 80 papers in international journals and conferences. 王小明(1964—),男,甘肃天水人,2005年于西北大学获得博士学位,现为陕西师范大学计算机科学学院教授、博士生导师,CCF高级会员,主要研究领域为无线传感器网络,移动自组织网络,普适计算,社会计算等。发表学术论文80余篇,出版专著2部,主编并出版教材1部。 LIN Yaguang was born in 1990. He is an M.S. candidate at School of Computer Science, Shaanxi Normal University. His research interests include opportunistic network and social network, etc. 林亚光(1990—),男,陕西渭南人,陕西师范大学计算机科学学院硕士研究生,主要研究领域为机会网络,社会网络等。 ZHANG Dan was born in 1991. She is an M.S. candidate at School of Computer Science, Shaanxi Normal University. Her research interests include opportunistic network and social network, etc. 张丹(1991—),女,甘肃酒泉人,陕西师范大学计算机科学学院硕士研究生,主要研究领域为机会网络,社会网络等。 Message Forwarding Strategy Based on Markov Decision Process in Opportunistic Networks* ZHANG Yang1,2, WANG Xiaoming1,2+, LIN Yaguang1,2, ZHANG Dan1,2 ZHANG Yang, WANG Xiaoming, LIN Yaguang, et al. Message forwarding strategy based on Markov decision process in opportunistic networks. Journal of Frontiers of Computer Science and Technology, 2016, 10(1):82-92. Abstract:To improve the delivery rates, control overhead rates and reduce the average delay is the ongoing research in the random opportunistic networks moving scenes. Due to the opportunistic network structure is sparse and the network topology is variable, the efficiency of single copy routing forwarding strategy is very low. This paper defines a forwarding strategy based on Markov decision by combining the similarity between Brownian motion of pollen and nodes random movement in opportunity networks and analyzing the law of the random motion of nodes. In the case of an appropriately growing average delay, the strategy can control the overhead rates and advance the delivery rates. Finally, this paper verifies the correctness of the theoretical models by simulation experiments. Key words:opportunistic network; Markov decision; delivery rate 文献标志码:A 中图分类号:TP393 doi:10.3778/j.issn.1673-9418.1504001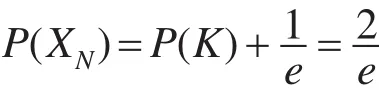
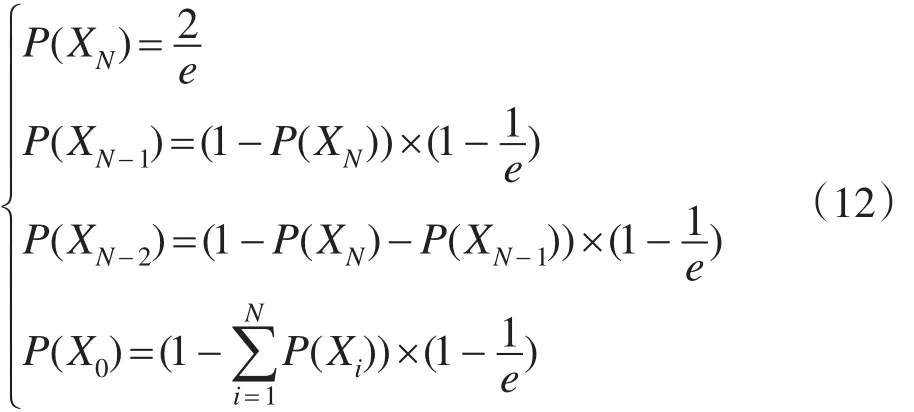
4 实验评估
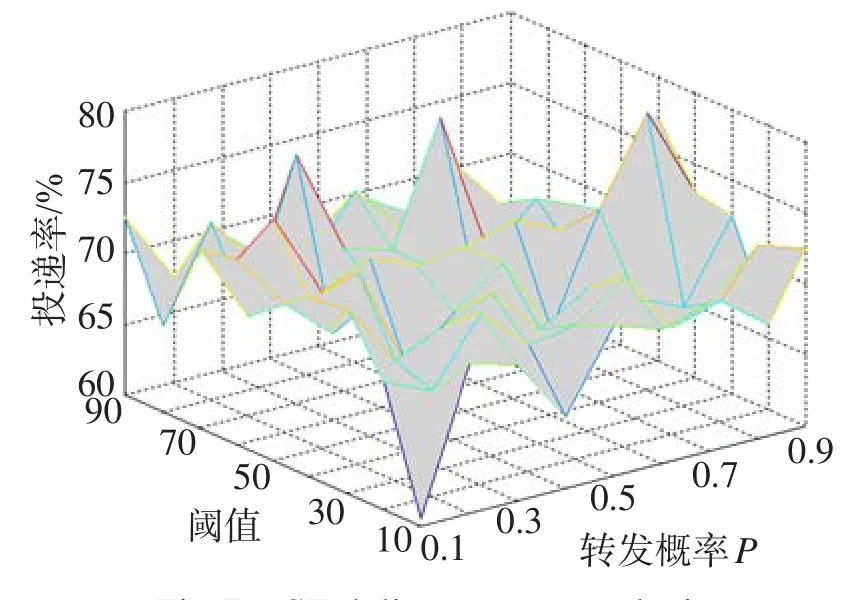
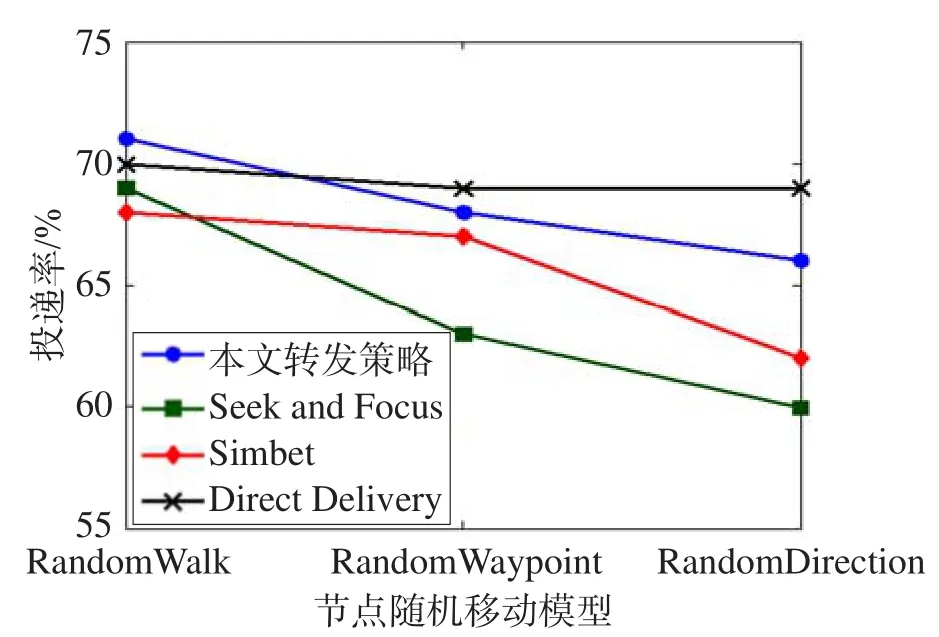


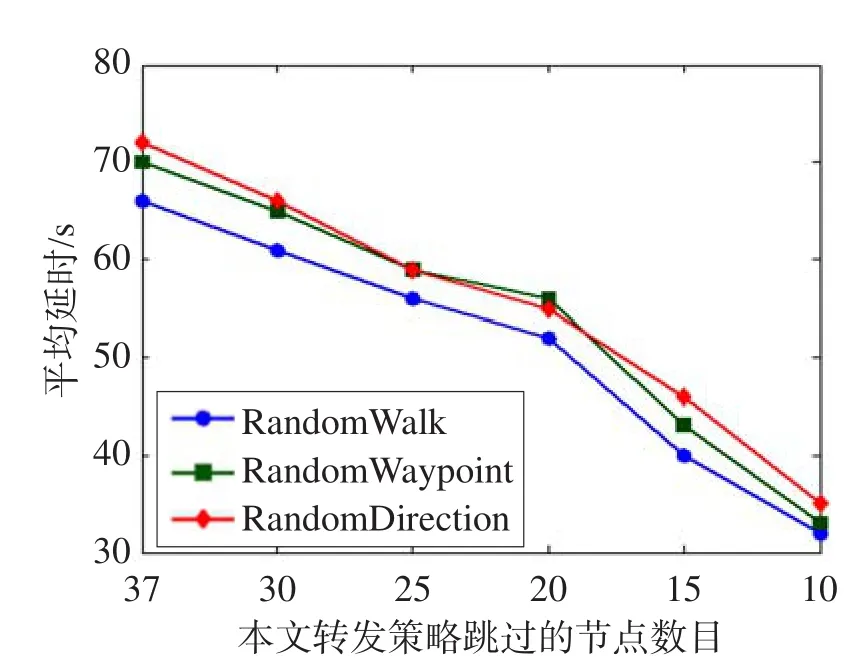
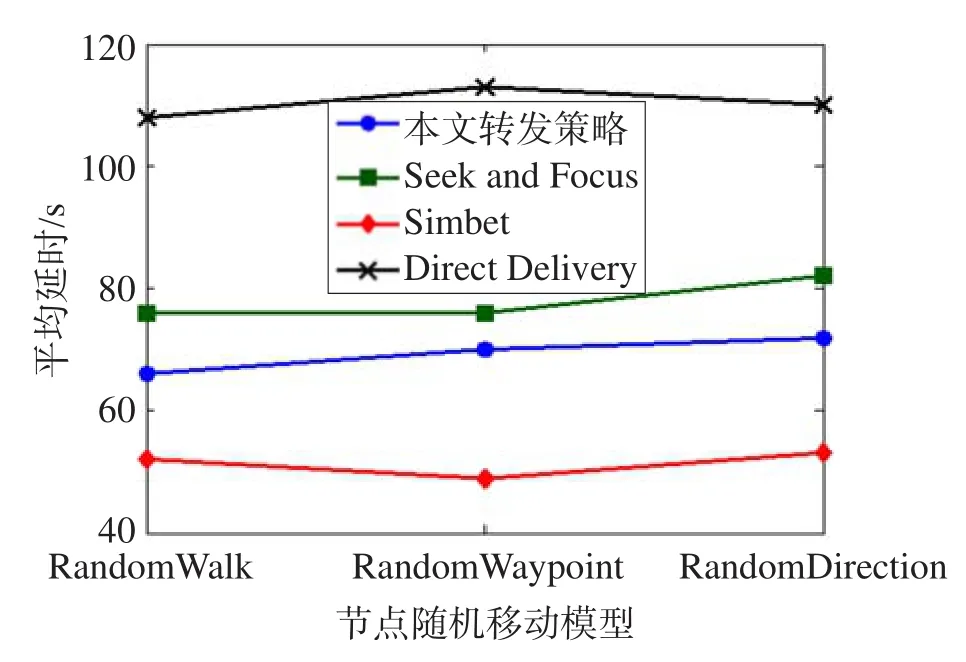
5 结束语




1. Key Laboratory of Modern Teaching Technology, Ministry of Education, Xi’an 710119, China
2. School of Computer Science, Shaanxi Normal University, Xi’an 710119, China
+ Corresponding author: E-mail: wangxm@snnu.edu.cn

