基于ARIMA模型的台风频次预测
刘珊,陈幸荣,蔡怡
(国家海洋环境预报中心,北京100081)
基于ARIMA模型的台风频次预测
刘珊,陈幸荣,蔡怡
(国家海洋环境预报中心,北京100081)
摘要:基于日本东京台风中心的逐月台风生成频次资料,为最近30 a的台风逐月生成频次时间序列建立了合适的ARIMA乘积季节模型,并用该模型对2010—2014年的台风逐月生成频次进行了预测。结果表明:时间序列中的ARIMA乘积季节模型在预测台风频次方面具有一定的预测技巧,除2013年外,其余4 a模型提前1 a预测的全年台风生成总数的异常情况均与观测一致。
关键词:台风生成频次;时间序列分析;ARIMA模型
1 引言
台风是夏秋季节影响我国东部沿海地区的最重要灾害性天气系统。每年因台风引起的直接和间接自然灾害给人民生命和国家财产造成的损失十分巨大。
提高台风灾害的预测水平是增强台风防御能力和减轻台风灾害损失的有效手段。在台风预测方面,李祚泳等[1-2]尝试用人工神经网络方法和投影寻踪回归方法对台风次数做出预测;Chan等[3-4]利用ENSO各项指数、东亚及西北太平洋的环流因子及南方涛动指数,澳大利亚季风强度和南太平洋副高强度等作为影响因子,建立统计模型来预测西北太平洋地区的热带气旋活动;范可[5]研究了冬春季大气环流对台风生成频次的影响,并确定了冬春季的北太平洋海冰面积指数和春季北太平洋涛动指数为新预测因子,并在此基础上建立了新的预测模型。然而,影响台风生成的因子众多且相互之间关系复杂,所以对台风生成频次的预测并非易事。上述工作在不同的方面对台风频次预测进行了探索,但目前,台风生成频次的预测准确度仍然较低,还远不能满足防灾减灾的实际需要。因此,尝试不同的方法预测台风生成频次,进一步提高台风生成频次的预测准确率仍然十分必要。
时间序列分析是一种动态数据处理的统计方法,该方法基于随机过程理论和数理统计学方法,研究随机数据序列所遵从的统计规律,具有结构简单,建模速度快,预测精度高等特点。目前,时间序列分析广泛应用在商业、气象、农业、生物科学等各领域。在本文中,我们将采用时间序列分析方法对西北太平洋台风的生成频次进行建模和预测,以期望该模型在预测台风生成频次方面有较好的结果,并能够应用到业务预测中为防灾减灾的实际需要提供科学参考。
2 资料和方法
本文中用到的1981—2013年逐月的台风生成频次资料来自日本东京台风中心。本文所采用的方法主要是ARIMA乘积季节模型。
20世纪70年代,美国统计学家Box和英国统计学家Jenkins提出了一整套关于时间序列分析、预测和控制的方法,被称为Box-Jenkins建模方法。求和自回归移动平均ARIMA(Autoregressive integrated moving average)模型是这一系列模型中最为基本的模型之一,现被广泛地应用在自然科学、工程技术和社会科学的诸多领域[6]。
ARIMA(p,d,q)模型的基本结构如下:

式中:xt为时间序列X=(x1,x2,x3,…,xt,…,xn)在t时刻的观测值;B为延迟算子,有Bpxt=xt-p;∇d为d阶差分算子,有∇d=(1-B)d;Φ(B)为平稳可逆ARMA(p,q)模型的自回归系数多项式,有
Θ(B)为平稳可逆ARMA(p,q)模型的移动平滑系数多项式,有为零均值白噪声序列。
当一个时间序列存在季节效应,且这种季节效应与长期趋势效应和随机波动之间存在着复杂的相互关系,简单的ARIMA模型不足以提供其中的相关关系,这时就需要ARIMA乘积季节模型。ARIMA乘积季节模型是随机季节模型与ARIMA模型的结合,一个阶数为(p,d,q)×(P,D,Q)S的ARIMA乘积季节模型结构如下:
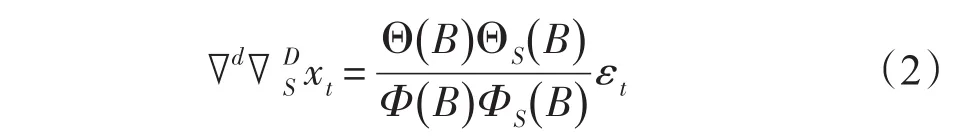
式中:∇DS为D阶以周期S为步长的季节差分运算,,其余变量及符号的意义与(1)式相同。
在实现建模的过程中,我们选择的应用软件为R。R软件是一种可用于统计计算和作图的编程语言及环境,可提供广泛的统计操作和作图技术,并且具有良好的可扩展性[7-9]。在建立模型的过程中,我们首先基于1981—2009年的逐月台风生成频次数据建立了针对2010年的逐月台风生成频次的季节乘积模型,然后在1981—2009年数据的基础上补充2010年的数据作为建模样本,建立针对2011年的逐月台风生成频次模型;之后以此类推,分别建立针对2012、2013和2014年的逐月台风生成频次模型。
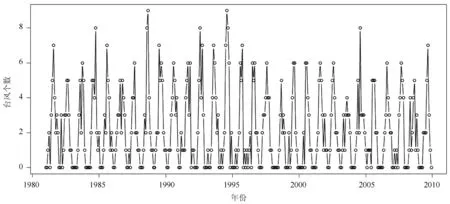
图1 1981—2009年逐月台风生成频次序列
3 建模过程
下文中我们以针对2010年逐月台风生成频次的建模过程为例,介绍适用于台风生成频次的ARIMA乘积季节模型的建立过程。建立乘积季节模型分为以下4个步骤:时间序列的平稳化,建模前的“白噪声”检验,模型的识别、定阶和参数估计以及模型参数和残差检验。
3.1时间序列的平稳化
在利用ARIMA模型进行建模之前,首先需要对时间序列的平稳性进行检验。平稳性检验有2种常用方法,一是直接通过时序图的特征进行判断,二是构造检验统计量进行假设检验,常用的平稳性统计检验方法是单位根检验(unit root test)。
图1是1981—2009年逐月的台风生成频次。从图中可以看出:该时间序列没有明显的长期趋势,但存在较为明显的年循环。另外,近30 a的逐年台风生成总频次序列也不存在明显的多年周期(图略)。所以,在建立ARIMA模型前首先需要对现有的时间序列进行平稳化处理。
由于该序列存在较为明显的年变化,故首先进行步长为12个月的季节变换,去除年循环。
进行过季节差分的时间序列如图2所示,原始的台风生成频次序列进行季节变换后,变成了既没有长期趋势又不存在明显周期的平稳时间序列。单位根检验的结果也证实了变换后序列平稳这一结论。
单位根检验计算得到的p值为0.01,小于选定的显著性水平0.05,则可以拒绝序列非平稳的原假设,认为变换之后的序列平稳。
3.2建模前的“白噪声”检验
建模前的“白噪声”检验是建模前的一个重要步骤。值得指出的是,并非所有的平稳时间序列都存在分析的价值和待挖掘的相关关系。平稳时间序列中存在一种“白噪声”序列,这种序列中各个序列值彼此之间没有任何相关性,过程是纯随机的,即该序列是一个没有记忆的序列,过去的行为对将来的发展没有丝毫的影响,所以从统计分析角度而言,“白噪声”序列虽然为平稳序列,但没有任何分析的价值。所以,在得到平稳化的序列之后,我们要对平稳序列进行“白噪声”检验,以确认该平稳序列非“白噪声”序列,存在继续分析的价值。

表1 季节差分序列的Ljung-Box检验结果
我们利用Ljung-Box方法对经过季节变换的台风生成频次序列(见图2)进行了白噪声检验,结果如下:
取显著性水平0.05,可以发现:经过季节变换的台风逐月生成频次序列在延迟6阶时,检验结果p值大于显著性水平,但是在延迟12阶时,检验结果p值远远小于显著性水平。这表明:变换后的序列在某些延迟阶数仍然具有明显的相关关系,可以拒绝序列为纯随机白噪声的原假设,认为序列中仍然存在待挖掘的相关关系,需要进一步的分析。

图2 经过季节差分的逐月台风生成频次序列
3.3模型的识别、定阶和参数估计
接下来我们开始对进行过季节差分变换的逐月台风生成频次序列进行ARIMA建模。在建立模型之前,首先计算该序列的自相关系数和偏自相关系数,以便确定建立ARIMA模型的类型和阶数。
图3和图4分别是经过季节差分变换后的台风生成频次序列的自相关图和偏自相关图。
可以发现:序列的自相关系数在落后12阶时明显超出了2倍的标准差范围,而偏自相关系数则是在落后12阶和24阶时明显超出了2倍的标准差范围。这表明差分后的序列仍含有一定的季节效应。但是无论是自相关系数还是偏相关系数,在1—12阶的范围内,相关系数都大体落在2倍标准差范围内,没有值显著的超出2倍标准差范围,这表明差分后的序列的短期相关性不明显。

图3 经过季节差分的台风生成频次的自相关图

图4 经过季节差分的台风生成频次的偏自相关图
根据上述分析,我们对台风生成频次的ARIMA乘积季节模型进行定阶。首先,自相关图和偏自相关图显示12阶以内的自相关系数和偏自相关系数都未明显超出2倍标准差范围,故认为差分后的序列没有明显的短期相关,所以尝试ARIMA季节模型的p,d,q均取值为0。再考虑季节自相关和偏自相关特征,即考察延迟12阶、24阶等以周期长度为单位的自相关系数和偏自相关系数特征,发现季节自相关系数截尾,偏自相关系数拖尾,故尝试ARIMA季节模型的P,Q取为0和1。因为目前我们已经对原始的台风生成频次序列进行过一次季节差分,所以这里D取值为1。综上所述,我们要拟合的乘积季节模型为ARIMA(0,0,0)× (0,1,1)12。
R计算得到的模型待估参数为-0.8842,所以据此写出的拟合模型为:
∇12xt=(1+0.8842B12)εt(3)
3.4模型参数和残差检验
对拟合模型进行检验,包括对模型中待估参数的显著性检验和对模型残差的“白噪声”检验两部分。
首先对待估参数的显著性进行检验。模型中的待估参数为-0.884 2,其标准误差为0.041 2,所以模型的真值在区间(-0.884 2±0.041 2)内,显著不为零,所以我们模型中得到的待估参数是显著的。
接着对模型残差进行检验。我们对模型的残差进行“白噪声”检验的目的是为了检查建立的ARIMA乘积季节模型是否充分提取了台风生成频次序列中的有效信息,此次进行的“白噪声”检验与建模型之前的“白噪声”检验目的不同,我们希望模型的剩余残差是完全随机的序列,即我们的模型已将有效信息全部提取。
模型残差的“白噪声”检验结果如表2所示:

表2 模型残差的Ljung-Box检验结果
从表2的结果中可以看到:无论是延迟6阶还是延迟12阶的p值都显著大于0.05。这表明,我们没有理由拒绝残差为白噪声的原假设,即建立的模型残差通过了“白噪声”检验。
4 预测
在建立合适的ARIMA乘积季节模型之后,我们利用该模型对2010年的逐月台风生成频次进行了预测。
图5给出了由模型预测的2010年逐月台风生成频次。蓝色虚线为拟合结果,蓝色实线为预测结果,黑色实线为观测结果。可以看到,模型对台风逐月生成频次的拟合很好,两者之间的相关系数达到0.84,而且2010年的台风逐月生成频次的预测结果跟观测结果是非常一致的。
为了更全面的检查ARIMA乘积季节模型在预测台风逐月生成频次上的表现,我们在1981—2009年逐月台风生成频次序列的基础上依次逐年补充了2010—2013年的逐月台风生成频次,并按照上文中的步骤重新进行了建模和预测(图略)。

图5 根据ARIMA(0,0,0)×(0,1,1)12模型预测的2010年逐月台风生成频次

图6 2010—2014年预测与观测的台风逐月生成频次距平同号率
分析2010—2014年的预测结果表明:在全年台风生成总频次异常方面,预测模型有着不错的表现。2010—2014年中,除2013年外,其余4 a模型提前一年预测的台风生成总频次异常情况与观测一致。在台风生成较活跃的6—10月份,模型在2010、2011、2014年表现良好,且对这3 a中6—10月台风生成总数的异常偏多偏少情况预测正确,但对2012 和2013年6—10月台风生成频次预测情况不够理想,表现为没有预测出这2 a 6—10月台风生成偏多的情况。
图6为2010—2014年预测台风逐月生成频次与观测台风逐月生成频次的距平同号率分布。可以看到:模型预测与观测台风逐月生成频次的距平同号率存在月际间的差别,其中表现最好的为11月和12月,最差的为5月。这表明,在台风的逐月生成频次上,11月和12月的台风生成频次的季节相关性最好,5月最差。这种预测技巧上的月际差别主要是因为5月是春夏转换的季节,台风生成源地的热力和动力条件变化较剧烈,造成该月台风生成频次的年际变化较大;而11、12月都属于一年中台风活动最不活跃的月份,年际变化较小。
5 总结与讨论
本文基于时间序列分析中的ARIMA乘积季节模型,通过序列平稳化,建模前的“白噪声”检验,模型的识别、定阶和参数估计以及模型参数和残差检验等步骤为最近30 a的逐月台风生成频次序列建立了合适的ARIMA乘积季节模型,并用该模型对2010—2014年的台风逐月生成频次进行了预测。结果表明:模型提前一年预测的2010、2011、2012和2014年台风全年生成总频次异常与观测吻合。在台风生成较活跃的6—10月,模型能够正确预测出2010,2011及2014年活跃期内台风生成偏多或偏少的情况,但对2012和2013年6—10月台风生成频次异常情况的预测不够理想。另外,模型预测与观测台风逐月生成频次的距平同号率存在月际差别,11月和12月最好,5月最差。
另外,值得指出的一点是,虽然利用时间序列预测模型对时间序列进行分析预测时只考虑历史时间序列的变化而不直接考虑其他因素对时间序列的影响,但这并不等于完全忽视这些因素的影响,因为时间序列本身正是在各种相关因素的相互作用下形成的。对历史数据变动规律的概括,也正是对各种复杂因素影响时间序列规律的概括[10]。从模型预测的台风生成频次的结果来看,ARIMA乘积季节模型对台风生成频次有一定的预测能力,且在某些年份有非常不错的表现,但漏报和错报的问题也仍然存在。在以后的工作中,我们会继续研究优化模型的方法,进一步提高台风频次的预测水平。
参考文献:
[1]李祚泳,邓新民.人工神经网络在台风预报中的应用初探[J].自然灾害学报, 1995, 4(2): 86-90.
[2]李祚泳,邓新民,桑华民.台风登陆华南年频次的投影寻踪回归预测模型[J].热带气象学报, 1998, 14(2): 181-185.
[3] Chan J C L, Shi J E, Lam C M. Seasonal Forecasting of Tropical Cyclone Activity Over the Western North Pacific and the South China Sea[J]. Weather and Forecasting, 1998, 13(4): 997-1004.
[4] Chan J C L, Shi J E, Liu K S. Improvements in the Seasonal Forecasting of Tropical Cyclone Activity Over the Western North Pacific[J]. Weather and Forecasting, 2001, 16(4): 491-498.
[5]范可.西北太平洋台风生成频次的新预测因子和新预测模型[J].中国科学D辑:地球科学, 2007, 37(9): 1260-1266.
[6]彭志行,鲍昌俊,赵杨,等. ARIMA乘积季节模型及其在传染病发病预测中的应用[J].数理统计与管理, 2008, 27(2): 362-368.
[7] Teetor P. R语言经典实例[M].李洪成,朱文佳,沈毅成,译.北京:机械工业出版社, 2013.
[8] Cryer J D, Chan K S.时间序列分析及应用[M].潘红宇,译.北京:机械工业出版社, 2011.
[9]王燕.应用时间序列分析[M]. 3版.北京:中国人民大学出版社, 2012.
[10]张利.基于时间序列ARIMA模型的分析预测算法研究及系统实现[D].镇江:江苏大学, 2008.
Typhoon generation frequency prediction based on ARIMA model
LIU Shan, CHEN Xing-rong, CAI Yi
(National Marine Environmental Forecasting Center, Beijing 10081 China)
Abstract:In this paper, an ARIMA product seasonal model is established for the monthly typhoon generation frequency time series during the last 30 years based on the monthly typhoon generation frequency data from Tokyo typhoon center of Japan. The monthly typhoon generation frequency prediction for the years 2010—2014 is completed through this model. The results show that, the ARIMA product seasonal model performs quite well in predicting the typhoon generation frequency. Except for 2013, the anomalies of the total annual typhoon generation frequency of the remaining four years predicted one year in advance by this model are all consistent with the observations.
Key words:typhoon generation frequency; time series analysis;ARIMAmodel
作者简介:刘珊(1986-),女,助理研究员,博士,主要从事短期气候预测方面的研究。E-mail: liushan@nmefc.gov.cn
基金项目:海洋公益性行业科研专项经费项目(201505013);国家自然科学基金项目(41440039)。
收稿日期:2015-12-26
中图分类号:P444
文献标识码:A
文章编号:1003-0239(2016)01-0053-06

