浙江沿海热带气旋风场兰金涡旋模型的检验与优化

涂小萍，王武军，郑健，蒋璐璐，谢华

（1.宁波市气象局，浙江宁波315012；2.宁波大学宁波市非线性海洋和大气灾害系统协同创新中心，浙江宁波315211；3.浙江省气象科学研究所，浙江杭州310008）



浙江沿海热带气旋风场兰金涡旋模型的检验与优化

涂小萍1,2,3，王武军1，郑健1，蒋璐璐1，谢华1

（1.宁波市气象局，浙江宁波315012；2.宁波大学宁波市非线性海洋和大气灾害系统协同创新中心，浙江宁波315211；3.浙江省气象科学研究所，浙江杭州310008）

摘要：基于2010—2013年严重影响浙江沿海的热带气旋资料、浙江省自动气象站及宁波凉帽山370 m高塔资料，引入兰金涡旋模型，提出一种最大风速半径计算方案，进行最大风速半径和不同形状因子的试验和检验分析。结果发现：对于严重影响浙江沿海海面的热带气旋，选择适当形状因子的兰金涡旋模型是适用的，形状因子与热带气旋结构有关，对强风带范围大的热带气旋形状因子取值相对大,形状因子在0.8—1.1之间得到浙江沿海站点兰金风速平均误差最小值。气象站点距离海岸线远近对兰金风速误差有最重要的影响，站点越远离海岸线，其兰金模型风速越接近实况，站点越靠近海岸线，其兰金风速越容易比实况偏强。多元回归订正能在一定程度上减小兰金风速误差。宁波凉帽山高塔资料分析表明：选择适当的形状因子可使得拟合边界层风廓线更接近于实况。

关键词：兰金涡旋；形状因子；热带气旋；边界层；浙江

1　引言

热带气旋(Tropical Cyclone，简称TC)是热带海洋上形成的一种灾害性天气系统，它引起的巨浪、风暴潮、狂风暴雨等经常给沿海地区造成重大损失。浙江省是受TC影响较多的沿海省份，登陆和影响浙江的热带气旋主要集中在7—9月[1]。TC结构、移动速度、移向的不同都会导致风雨影响程度的差异[2]。20世纪90年代以来随着多普勒雷达在我国的组网建设，对TC登陆后的边界层结构有了新的研究和进展，基于相关性追踪技术（Tracking Radar Echoes by Correlation,简称TREC）[3]，地基雷达轨迹显示技术（Ground Based Velocity Track Display,简称GBVTD）[4]的TC边界层结构研究取得了很多成果[5-6]。这些研究主要针对登陆TC的非对称结构变化进行，为TC登陆后的大风和降水预报提供了重要参考。

由于洋面上观测资料稀少，模型风场被广泛用于TC结构的研究中，其中不乏简单实用的，如朱首贤等[7]建立的基于特征等压线的不对称型气压场和风场模型，但兰金（Rankine）组合涡仍是气象学上最常用的TC物理模型，该模型基于最大风速的风场分布，可应用于估算广阔洋面上的TC风场分布。2006年Macafee和Pearson[8]基于多种资料，对包括兰金涡旋模型在内的5种TC参数化风场进行对比分析，并在兰金涡旋模型中考虑了一定的形状因子，结果发现：TC不同象限最大风速半径（Rmax）不是对称变化的，Rmax的大小与中心附近最大风速（Vmax）有关，Vmax越大，Rmax的不对称性越小，与浮标站观测对比，对16 m/s及以上的风力，选择适当参数后的模型风速与浮标站观测平均误差可以小于1 m/s。许映龙等[9]在一定的假设前提下，利用兰金涡旋模型构造TC风场，并将构造的理想风场与两种基于多普勒雷达径向速度场确定的TC风场进行对比。2008年颜文胜等[10]在兰金涡旋运动模式基础上模拟TC的水平风场结构，证明环境风的分析判断对近海TC的移动路径预报有很好的指示意义。藏增亮等[11]在研究多普勒天气雷达径向风场反演散度场时利用兰金涡旋构造了一个只有气旋式旋转的切向风速理想场，其结果也表明了对气旋采用兰金涡旋理论是科学合理的。

经典兰金涡旋模型中最重要的参数是最大风速半径R。2004年胡邦辉等[12]对藤田气压模式经合理的简化和推导，提出了一个针对稳定状态的海面移动非对称TC的最大风速半径计算方案，其研究表明：TC最大风速半径与中心附近最大风速、中心气压、环境温度和气压、摩擦系数等相关。陈德文等[13]基于QuikSCAT风场和美国联合台风预警中心的TC资料，将遥感平均风剖面与Holland台风模型进行最小二乘法拟合来反演TC最大风速半径，取得了较好效果。在假设TC环流完全对称的前提下，多普勒雷达基速度资料广泛应用于TC定位和R的确定中，但由于多普勒雷达速度资料的半径在230 km以内，定位对资料的质量要求非常之高，速度模糊甚至距离模糊存在都会导致定位失败[14]。

目前TC数值模式中普遍采用将TC Bogus方案叠加于分析场中形成初始场，兰金涡旋模型就是一个理想化的TC Bogus方案[15]。为了提高Bogus方案对TC不对称性的描述，很多气象专家结合观测事实，采用不同的方法构造TC Bogus模型，通过不同TC个例的试验表明可以改善数值模式对TC的预报效果[16-18]。根据Macafee和Pearson的研究，引入适当的形状因子有可能减小兰金模型风速误差。TC靠近陆地时常常发生变形，对于不同象限的TC风场考虑不同的形状因子有可能减小兰金模型风速误差，因此有必要加强靠近陆地的TC风场兰金涡旋模型适用性的研究。

对浙江省造成直接影响、间接影响和影响程度介于二者之间的TC个数分别为39.5%、41.6%和18.9%，其中直接影响类TC一般稳定西北行，强度强，在厦门以北到浙江沿海登陆，往往给浙江陆地和沿海带来狂风暴雨，间接影响类TC风雨灾害程度相对较轻，而介于直接影响和间接影响之间的TC一般在125°E以西紧靠浙江沿海北上，主要灾害为海上大风[19]。本文引入兰金涡旋模型，适当考虑形状因子B进行试验，以1211强台风“海葵”为例详细介绍分析方法，对2010—2013年严重影响浙江沿海海面的6个TC个例进行适用性检验，目的是利用沿海多种测风资料对兰金涡旋模型进行检验，特别是针对TC受到陆地摩擦影响下不同形状因子的误差情况进行分析，为TC海面风分布的预报服务和防台抗台提供科学依据。对于缺少观测资料的东海海面，本文的工作也为大风服务提供参考。

2　资料和方法

2.1资料

TC个例的选择：选择2010—2013年间，经过以30°N、122°E为圆心，3.5个纬距为半径范围，在浙江沿海海面风力达到严重影响程度（浙江沿海210个气象站中至少有1个站点阵风达10级及以上）的TC为分析对象[19]，共计6个TC满足条件，路径见图1。影响时段选择沿海有站点进入TC 7级风圈开始到站点10 min平均风速减小到6级以下，分析针对全风速进行，各TC资料时段见表1。

表1　TC个例概况

TC定位定强和站点观测资料：TC资料为中央气象台（CMO）实时业务定位定强资料，站点风速为逐10 min平均风速，资料来自浙江省气象信息中心。气象站点资料入库时均经过自动质量控制和人工审核，应用这部分资料时本文没有进行质量控制。

宁波凉帽山高塔资料：高塔位于宁波凉帽山岛（29.911°N、122.024°E，塔基海拔20 m），距离大陆海岸线约2 km，塔高370 m，在相对塔基32、60、89、139、179、212、263和298 m的南北两个方向分别安装了气象观测仪器，进行温、湿（温湿传感器为HMP45D型）和风（二维超声风速仪，德国THIES公司生产）的观测，塔基安装自动气象站和二维超声风速仪进行同步观测，多套仪器同步观测是用于设备备份及资料质量控制[20]。本文所用高塔资料时间为2012年8月7日00时—8月8日03时(北京时，下同)，均经过人工审核，其中199、318 m两层仅北侧有观测资料，其他层次取南北观测资料均值。

图1　TC个例路径

图2　进入TC最大风速半径R的站点兰金风速RV与r变化示意图

2.2研究方案

对于进入TC最大风圈半径R的气象站点，在TC中心靠近和远离的过程中，最大风速半径R随时间有所改变，但总体变化不大，必然有两个时刻站点与TC中心距离r等于兰金最大风速半径R，即r= R，在完全满足兰金涡旋模型的情况下，这两个时刻站点切向风速V等于Vmax，两风速峰值中间存在风速谷值对应r＜R且极小（见图2）。

以CMO逐小时业务定位和定强为基础，引入考虑形状因子的兰金涡旋模型模拟TC风场结构[9,15]，则距离TC中心r点的涡旋切向风速分布满足式（1）：

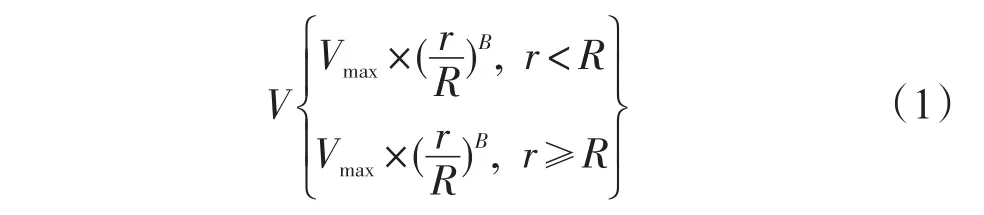
式中：B为形状因子，B=1.0时即为标准兰金涡旋模型，Vmax为TC中心附近最大风速（取CMO逐小时主观定强风速），R为Vmax所在半径，V为半径r处的切向风速。Macafee和Pearson在应用兰金涡旋模型研究大西洋飓风时认为形状因子取0.5可以适用于中纬度TC，本文分别对B从0.5—1.2间隔0.1的逐个形状因子试验。

业务工作中海面风的预报和服务是针对海平面10 m高度，浮标站测风被认为具有最好的代表性。浙江沿海布有温州、舟山两个浮标站，假设TC影响时浮标站风速满足兰金涡旋模型，在式（1）中已知TC中心附近最大风速Vmax、站点逐小时观测风速（式中V）和TC中心与站点距离（式中r），即可推算出逐小时最大风圈半径R。根据R、Vmax和r，则可推算各站点兰金涡旋模型风速（下称RV）。各站点RV与观测风速（下称V）会有差异，对每个TC影响期间不同形状因子的逐小时兰金风速误差（下称δ，为兰金风速与实测风速差值，δ=RV-V）求时间平均，平均误差越小说明形状因子B的取值更佳。将逐小时兰金风速误差与站点信息进行多元回归，根据回归方程对沿海站点δ进行订正，通过订正前后的兰金风速误差对比来考察订正效果。研究步骤与内容如图3。

图3　不同形状因子B误差试验及适用性检验研究步骤与内容

图4　1211“海葵”的兰金涡旋模型误差随形状因子的变化

3　结果分析

3.1“海葵”兰金涡旋模型应用分析

参与试验的6个TC中，只有1211“海葵”穿越了浙江省陆地，距离宁波凉帽山高塔最近，下文以“海葵”为代表进行详细分析。根据预定计算方案，“海葵”影响期间共有3410站次达到标准，根据式（1）计算逐时次形状因子为0.5—1.2的兰金涡旋模型风速并与实况比较，可计算出逐站次兰金涡旋模型风速误差，从而得到“海葵”影响期间浙江沿海兰金涡旋模型风速误差绝对值平均和误差平均随形状因子B的变化（见图4），可见B=0.9时两者均最小，其次是B=0.8和B=1.0，下面分析仅针对B=0.9和B=1.0的结果。

宁波北渔山、檀头山和台州的东矶岛（站点均位于浙江近海，具体位置在图6中分别以BYS、TTS 和DJ标注）进入了“海葵”最大风速半径内，站点与TC中心最近距离分别为10.7 km、22.2 km和28.7 km，3站点海平面气压都表现出明显的漏斗型特征。宁波多普勒雷达TREC风场资料表明：“海葵”眼区范围偏大，登陆前眼区直径超过50 km，登陆后范围更大，故认为这3个自动站不仅进入“海葵”最大风速半径内，而且TC中心还从站点附近经过。下面以东矶岛为例进行兰金涡旋模型和实况风速的对比分析。

图5为依据CMO业务定位定强及舟山浮标站资料，形状因子B分别为1.0和0.9，对应“海葵”逐小时兰金最大风速半径R1（B=1.0）和R2（B=0.9）、TC中心与东矶岛距离r、东矶岛实况风速V及兰金风速演变曲线对比（RV1为B=1.0时，RV2为B=0.9时）。可见2012年8月8日03时“海葵”登陆前20 min R1和R2均达到最小，分别为55 km、51.5 km，此时东矶岛距离TC中心r=35.7 km，事实上8月8日00—07时站点r均小于R1和R2，表明该时段站点位于兰金涡旋最大风速半径内。风速演变趋势分析表明“海葵”靠近东矶岛时站点风速持续增大，远离时持续减小，实况观测到2个风速峰值分别出现在8 月7日23时和8月8日07时，峰值间隔8 h，对应风速分别达到43.7 m/s和36.6 m/s。对比可见：兰金风速RV峰值与观测峰值出现时间基本一致，峰值出现时，r值接近R。东矶岛第一观测峰值出现时，RV1达到峰值46.1 m/s，RV2达到42.6 m/s的次峰值，此时站点r=80 km，接近R1=77 km和R2= 72 km。“海葵”远离过程中，东矶岛第二风速峰值出现时，对应兰金风速RV1=35.3 m/s和RV2=37.9 m/ s，也达到峰值附近，此时东矶岛r为61.8 km，也接近R1（66.5 km）和R2（61.9 km）。北渔山和檀头山的实测风速和兰金风速基本表现出相同的变化趋势，由于檀头山自动站靠近大陆海岸线，实况观测风速虽明显小于兰金涡旋模型，但观测风速V峰值出现时，RV1和RV2也达到峰值或次峰值，观测风速峰值出现时对应的r与R1和R2也基本接近。可见基于CMO对“海葵”业务定位定强和舟山浮标站风速资料计算的“海葵”兰金涡旋最大风速半径R1和R2均得到实况观测资料的验证，计算结果合理。

图5　“海葵”期间不同参数时间序列变化

图6　2012年8月7日23时浙江省自动站全风速（填色）、B=1.0（黑色实线）和B=0.9（黑色虚线）的兰金涡旋模型风速（灰色圆为B=1.0兰金最大风速半径）

图6为2012年8月7日23时东矶岛（DJ）观测到第一峰值时浙江省自动站实况全风速及B=1.0和B=0.9时的兰金涡旋模型风速空间分布，此时东矶岛靠近B=1.0的兰金最大风速半径并观测到最大风速43.7 m/s。图中可见：实测等风速线近似平行于海岸线自西向东增大，海岸线附近梯度最大。台州和宁波近海海面兰金风速等值线与实况更为接近，但实况在靠近海岸线的风速梯度明显大于兰金涡旋模型，表明沿海地区实况风速减小明显比兰金涡旋模型快。对比形状因子B=1.0和B=0.9时的兰金风速发现：B=0.9时近海海面兰金风速相对于B=1.0偏小但更接近实况，相同半径的兰金风速前者比后者风力偏小1级左右。

3.2回归订正对兰金风速的改进

3.2.1回归方程的建立及其对不同形状因子兰金风速的改进

形状因子B分别为1.0和0.9时，分析发现兰金涡旋模型风速误差δ与浙江沿海气象站点海拔高度、站点与大陆海岸线距离、观测时段风速标准差相关系数差异不大，B=1.0时分别为-0.234、-0.723、-0.421，B=0.9时则为-0.237、-0.720和-0.425，海拔高度因子通过0.05信度检验，后两个因子相关系数通过0.01信度检验，表明站点海拔高度对δ有一定影响，但不是重要因子。δ与站点海拔高度的负相关关系反映出海拔高度越低，地形摩擦作用越明显，实际观测风速越容易偏小，相同r时兰金风速越容易大于实测值，从而导致兰金风速越趋于正误差。δ与站点到大陆海岸线的距离相关系数达到-0.72，表明站点所在的地理位置对δ有最重要的影响，距离海岸线近的站点，地形作用相对明显，实况风速越容易偏小，在r相同的情况下，兰金涡旋模型容易表现出更大的正误差。|δ|（兰金风速误差绝对值）与站点到大陆海岸线的距离相关系数也达到-0.40左右，表明靠近海岸线的站点受地形影响相对大，|δ|越大，可见远离海岸线的站点更容易满足兰金涡旋模型。与观测时段风速标准差相关性表明：TC影响时段内风速起伏小的站点兰金风速越容易偏大，反之越容易偏小。

根据高塔所在位置，在浙江北部沿海87个站点中选择17个作为独立检验样本，其它70个站点作为回归样本，应用多元回归方法对δ与站点距海岸线距离、观测风速标准差及海拔高度进行多元回归分析，得到方程如下：

δ=7.95-1.2360V-0.0032H-0.130D（B=0.9时）（2）

δ=10.3-1.233V-0.034H-0.132D（B=1.0时）（3）

式中：δ为兰金风速误差，V为站点观测风速标准差，H为站点海拔高度（m），D为站点与大陆海岸线距离（km）。

经剩余17个独立样本检验（海拔高度8—414 m，海岸线距离12—90 km），回归后B=1.0的平均兰金风速误差绝对值平均由4.2 m/s减小到2.9 m/s，B= 0.9则由4.1 m/s减小到3.3 m/s，可见回归订正有较好效果。

3.2.2不同形状因子时高塔处的拟合兰金风廓线与实况的对比

从2012年8月8日03时30分开始宁波凉帽山高塔80 m及以上层次资料出错，因此本文仅对8月7日00时—8月8日03时“海葵”影响期间的高塔资料进行分析，结果只代表“海葵”登陆前高塔处的边界层特征。

将凉帽山高塔不同层次信息代入式（2）和（3），可计算出高塔不同高度δ，用兰金风速减去δ即得到高塔处方程拟合出的边界层兰金风廓线。

图7为8月7日00时—8月8日03时，形状因子分别为1.0和0.9时高塔处回归方程拟合的时间平均兰金风廓线与实况对比。B=1.0和B=0.9的两条拟合兰金风廓线最大误差值都出现在塔基，分别偏小4.7 m/s和2.3 m/s，而最小误差值均出现在52 m，分别为-1.8 m/s和0.2 m/s。从廓线趋势分析，B=1.0 和B=0.9的拟合风廓线与实况基本一致，但形状因子B=0.9时风廓线相对于B=1.0的风廓线系统性误差更小，B=0.9时塔层各层平均拟合误差绝对值平均比B=1.0减小2 m/s，结果更接近实况。可见选取合适的形状因子可以减小δ，应用中应当予以考虑。

图7　不同形状因子时宁波凉帽山高塔处的拟合兰金风廓线与实况对比

图8　严重影响浙江沿海TC的兰金涡旋模型平均误差随形状因子的变化

3.3不同形状因子的兰金涡旋模型的适用性检验

为了考察兰金涡旋模型的适用性，对2010—2013年间6个严重影响浙江沿海的TC进行分析（个例详情见表1和图1）。图8为所选TC个例形状因子B取0.5—1.2逐0.1计算得到的浙江沿海兰金涡旋模型误差绝对值平均（见图8a）和误差平均（见图8b）随B的变化曲线，图中黑色粗实线是样本数权重误差平均，图8可见B=0.9时兰金风速误差绝对值平均和误差平均均达到最小，其次是B=1.0和B= 0.8，且B越小兰金风速较实况偏小越明显（见图8b），个例分析发现，除1315“康妮”外，其它5个TC均在B=0.9附近出现误差绝对值平均的最小值（见图8a），平均误差表明各TC个例均在形状因子0.8—1.1之间出现最小误差，其中4个TC平均误差最小值出现在0.9—1.0。与Macafee等[8]的研究结果相比，本文得到的形状因子偏大，可能与TC源地不同有关。可见对于严重影响浙江沿海海面的TC，兰金涡旋模型是适用的，但应根据TC个例的不同结构考虑适当的B值。

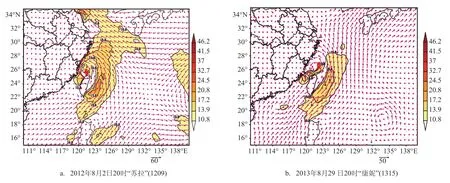
图9　两次TC影响时ECMWF细网格海平面10 m风初始场

图8分析得出1315“康妮”的兰金风速误差绝对值平均与其它5个TC表现不一样，且1315“康妮”和1209“苏拉”分别在B=0.8和B=1.1时得到兰金风速最小误差，其他TC均在0.9—1.0得到，这与TC结构不同有关。图9a和9b分别对应2012年8月2日20时和2013年8月29日20时“苏拉”和“康妮”ECMWF细网格10 m风场（0.25°×0.25°）。“苏拉”中心位于25.7°N、121.4°E，强风带主要位于TC中心北侧和东侧，7级等风速线范围影响到30°N以北，适当放大形状因子B才能使得兰金涡旋模型更接近于实况，最终试验结果“苏拉”的B=1.1时兰金风速误差最小；而浙江近海北上的1315“康妮”则不同，2013年8月29日20时中心位于26.6°N、122.3°E，分析发现“康妮”兰金风速误差表现与其结构明显不对称有关，其大风带位于TC中心的东侧，中心西侧风速普遍比东侧风速偏小10 m/s以上，减小B才能使得兰金涡旋模型更接近于实况，最终表现在B= 0.7时得到最小误差绝对值平均，B=0.8时得到最小平均误差。形状因子B是对标准兰金风速的放大或缩小，取值与TC结构相关，当强风带范围跨区大，实际风速也可能大，需要适当放大B值，反之，则需减小B的取值。

4　结论与讨论

基于浙江省气象站及宁波凉帽山高塔资料，引入兰金涡旋模型，考虑适当的形状因子B，对1211强台风“海葵”影响期间浙江沿海海面站点风和边界层观测资料的进行统计分析，并选择6个严重影响浙江沿海的TC个例进行最佳形状因子的试验和分析，结果表明：

（1）“海葵”影响期间通过站点测风资料确定兰金涡旋模型的最大风速半径，从而计算TC的兰金风速分布。与实况对比B=0.9时兰金风速相对于B=1.0偏小但更接近实况，相同半径的兰金风速前者比后者风力偏小1级左右；

（2）“海葵”影响期间浙江省气象站资料分析表明：站点距离海岸线远近对兰金风速误差δ有最重要的影响，站点越靠近海岸线，兰金风速越容易偏强，距离海岸线远的站点更容易满足兰金涡旋模型。多元回归能在一定程度上减小δ。宁波凉帽山高塔资料分析表明：形状因子为0.9相对于形状因子1.0时在高塔处风廓线有2 m/s左右的系统性误差的减小，结果更好；

（3）多个TC适用性检验发现：对严重影响浙江沿海的TC，形状因子在0.8—1.1之间得到浙江沿海站点兰金风速平均误差最小值，应用时可根据前期观测资料按文中方法计算兰金风速误差及TC结构来选择适当的形状因子。

本文试验对比了不同形状因子时兰金涡旋模型风速的总体误差表现，检验了兰金涡旋模型在浙江沿海的适用性。由于TC结构的不对称性，位于不同象限的TC形状因子取值可能有所不同，且形状因子会随时间变化而改变，尚待进一步研究和分析。

参考文献：

[1]朱业,丁骏,卢美,等. 1949-2009年登陆和影响浙江的热带气旋分析[J].海洋预报, 2012, 29(2): 8-13.

[2]俞燎霓,钱惠平,董美莹,等.热带气旋“麦莎”和“韦帕”在浙江产生大风对比分析[J].海洋预报, 2013, 30(3): 40-45.

[3] Tuttle J, Gall R. A Single-radar Technique for Estimating the Winds in Tropical Cyclones[J]. Bulletin of the American Meteorological Society, 1999, 80(4): 653-668.

[4] Lee W C, Marks Jr F D, Carbone R E. Velocity Track Display—A Technique to Extract Real-time Tropical Cyclone Circulations Using A Single Airborne Doppler Radar[J]. Journal of Atmospheric and Oceanic Technology, 1994, 11(2): 337-356.

[5]魏超时,赵坤,余晖,等.登陆台风卡努(0515)内核区环流结构特征分析[J].大气科学, 2011, 35(1): 68-80.

[6] Wang M J, Zhao K, Wu D. The T-TREC Technique for Retrieving the Winds of Landfalling Typhoons in China[J]. Acta Meteorologica Sinica, 2011, 25(1): 91-103.

[7]朱首贤,沙文钰,丁平兴,等.近岸非对称型台风风场模型[J].华东师范大学学报(自然科学版), 2002, (3): 66-71.

[8] Macafee A W, Pearson G M. Development and Testing of Tropical Cyclone Parametric Wind Models Tailored for Midlatitude Application—Preliminary Results[J]. Journal of Applied Meteorology and Climatology, 2006, 45(9): 1244-1260.

[9]许映龙,矫梅燕,毕宝贵,等.近海台风雷达定位方法应用研究[J].大气科学, 2006, 30(6): 1119-1128.

[10]颜文胜,林良勋,翁向宇,等.多普勒天气雷达速度图像在近海台风移动路径预报中的应用[J].热带气象学报, 2008, 24(6): 665-671.

[11]臧增亮,吴海燕,黄泓.单多普勒雷达径向风场反演散度场的一种新方法[J].热带气象学报, 2007, 23(2): 146-152.

[12]胡邦辉,谭言科,王举.热带气旋海面最大风速半径的计算[J].应用气象学报, 2004, 15(4): 427-435.

[13]陈德文,董剑,袁方超.基于QuikSCAT卫星遥感风场的台风最大风速半径反演及个例分析[J].海洋通报, 2012, 31(4): 376-383.

[14]周仲岛,郑秀明,张保亮.都卜勒雷達在颱風中心定位與最大風速半徑決定的應用[J].大气科学(中国台湾), 1996, 24(1-2): 1-24.

[15]王亮,陆汉城,付伟基,等.人造台风模型中三维风场的改进及敏感性模拟研究[J].气象科学, 2008, 28(6): 606-613.

[16]王亮,陆汉城,潘晓滨,等.非对称台风风场的动力初始化应用研究[J].气象科学, 2009, 29(6): 720-726.

[17]瞿安祥,麻素红.非对称台风bogus方案设计和初步试验[J].应用气象学报, 2007, 18(3): 380-387.

[18] Wang S D, Liu J J, Wang B. A New Typhoon Bogus Data Assimilation and Its Sampling Method: A Case Study[J]. Atmospheric and Oceanic Science Letters, 2011, 4(5): 276-280.

[19]刘爱民,涂小萍,胡春蕾,等.宁波气候和气候变化[M].北京:气象出版社, 2009: 135-136, 149-150.

[20]涂小萍,姚日升,杨豪,等.一次入海温带气旋边界层气象要素观测分析[J].自然灾害学报, 2013, 22(5): 160-170.

Verification and optimization of the Rankine vortex model on TC wind fields over the offshore Zhejiang Seas

TU Xiao-ping1,2,3, WANG Wu-jun1, ZHENG Jian1, JIANG Lu-lu1, XIE Hua1
（1. Ningbo Meteorological Bureau, Ningbo 315012 China; 2. Ningbo Collaborative Innovation Center of Nonlinear Hazard System of Ocean and Atmosphere, Ningbo university, Ningbo 315211 China; 3. Zhejiang Institute of Meteorological Sciences,Hangzhou 310008 China）

Abstract：Based on the data of tropical cyclones (TC) severely affecting the offshore Zhejiang Seas from 2010 to 2013 and the automatic weather stations data of Zhejiang province and 370 meters tower at the Ningbo Liangmaoshan hill, a calculation method for radius of maximum wind (RMW) has been proposed with the Rankine vortex model. The experiments for testing RMW and influence factors on RMW are conducted. Results show that the Rankine vortex model is reasonable for those TCs severely affecting the offshore Zhejiang Seas when a proper shape factor is taken into account. The shape factor is related to a TC structure and small absolute errors can be got with shape factors between 0.8—1.1. Further analysis also shows the distance from the station to the coastal line is very important. The closer to the coastal line, the error is bigger. Multivariate regression analysis helps to decrease the Rankine vortex errors. The data at the Liangmaoshan tower indicates that a proper shape factor can make the Rankine vortex model wind profile closer to the observation in the boundary layer.

Key words：the Rankine vortex model; shape factor; tropical cyclones; boundary layer; Zhejiang province

作者简介：涂小萍（1968-），女，正研高工，硕士，主要从事天气预报和研究。E-mail: txp_hk@aliyun.com

基金项目：浙江省自然科学基金项目（LY15D050001）;宁波市科技计划项目(2012C50044)。

收稿日期：2015-07-29

中图分类号：P732.3

文献标识码：A

文章编号：1003-0239（2016）01-0019-08