多排行星齿轮动力耦合器的构型综合方法

李 斌，孙 涛，宋轶民，刘建平

（1. 天津大学机构理论与装备设计教育部重点实验室，天津 300072；2. 天津工业大学机械工程学院，天津 300387）



多排行星齿轮动力耦合器的构型综合方法

李 斌1, 2，孙 涛1，宋轶民1，刘建平1

（1. 天津大学机构理论与装备设计教育部重点实验室，天津 300072；2. 天津工业大学机械工程学院，天津 300387）

摘 要：根据行星齿轮机构的结构特点，提出了新三色拓扑图表示方法.将变胞机构的构态变换方法应用于混合动力汽车动力耦合器的构型综合，并将动力耦合器的多排行星齿轮机构的构型综合问题转化为行星齿轮机构邻接矩阵的运算问题.通过各阶段矩阵运算，将单排行星齿轮机构的邻接矩阵转换成多排行星齿轮的联合矩阵和邻接矩阵，进而得到多排行星齿轮机构的拓扑图和构型综合方案，为后续构型方案的同构判断提供数学模型.以双排和三排行星齿轮构型综合为例，得出多款行星齿轮拓扑构型方案，验证了上述方法的有效性，并采用模糊一致矩阵的优选方法得到几款适用于混合动力汽车动力耦合器的新型基础构型方案.

关键词：混合动力汽车；多排行星齿轮；构型综合；动力耦合器；三色拓扑图

网络出版时间：2014-09-19. 网络出版地址：http://www.cnki.net/kcms/doi/10.11784/tdxbz201405044.html.

在电动汽车的续航能力、可靠性、动力、使用寿命等关键技术完全成熟之前，考虑到环保、能源等问题的迫切性，各国越来越重视混合动力汽车（hybrid electric vehicle，HEV）的研发与推广.动力耦合器是HEV传动系统的关键部件.如何高效、灵活地实现发动机动力和电动机动力的合成、分解及方向变更，以支持多种混合驱动工作模式，已成为动力耦合器研发的核心问题，而发明具有工程实用价值的新型动力耦合器是有效解决上述问题的关键[1-3].

行星齿轮机构因具有结构紧凑、结合平顺性较好、耦合效率高等特点，已成为动力耦合器的首选解决方案，并成功应用于HEV传动系统，因涉及知识产权壁垒，目前各汽车制造企业都在积极研发自己的产品.

目前，对于行星齿轮机构的研究主要集中在对其运动学和动力学分析以及参数化设计方面，对于行星齿轮机构的构型综合方法研究较少.Hsu等[4]采用枚举的方式将构件数目为4的单自由度的行星齿轮机构综合为构件数目为6或7的行星齿轮机构.Li等[5]采用Schmidt等[6]提出的Graph-Grammar法，通过齿轮基元和载体基元合成得到齿轮机构的构型方案，并开发了行星齿轮方案生成工具.以上方法都是基于图论的方法，通过逐步添加节点和边（齿轮和运动副）构建综合方案.值得指出的是，通过该方式得到的拓扑图与机构简图没有一一对应关系，需要考虑齿轮啮合副的不同进行二次综合.Liu等[7]提出了基于运动分离的齿轮综合方法，薛隆泉等[8]提出了基于功能离散的周转轮系拓扑综合方法，通过拓扑演化和拓扑反演推导出周转轮系拓扑图谱和结构图谱，这些方法可得到丰富多样的行星齿轮机构构型方案，但是拓扑反演过程较复杂.朱福堂等[9]针对HEV的机电耦合机构，采用机械装置的创造性设计方法得到14 种6杆和7杆行星齿轮机构综合方案，该方法在综合过程中需要人为推导拓扑图的变换，其工作量比较大.

从现有的HEV产品和研究成果[10-12]看，混合动力汽车器动力耦合器的方案设计存在以下一些问题：拓扑构型不够丰富；构型结构设计大多依赖设计师的经验和试凑方式得到，构型综合尚缺乏系统性，无有效的理论支撑；目前现有的齿轮构型方法主要采用图论的方式，图形推导过程复杂，人工工作量大；已有的构型综合方法得到的构型方案往往存在大量不满足动力耦合器的动力耦合、分解以及转矩、转速双耦合模式的特定要求.基于此，本文研究了行星齿轮拓扑表示方法以及行星齿轮邻接矩阵的建立及运算法则，并借鉴变胞机构中的构态演变的数学描述方式，提出多排行星齿轮的拓扑构型综合方法；运用该方法可得到大量满足动力耦合器性能要求的基础构型方案，从中优选出新型方案，作为后续分析设计的参考方案；最后以双排和三排行星齿轮构型综合为例，验证本文方法的有效性.

1　行星齿轮多色拓扑图表示方法

如何对机构进行拓扑描述是机械创新和概念设计阶段所要解决的首要问题.自图论于1964年首次被引入机构学用于表示运动链的拓扑结构以来，由于以点表示构件、以边表示运动副的拓扑图与机构的结构简图之间具有明确的对应关系，且拓扑图又可以用矩阵表示，便于计算机处理，故图论为机构结构学的研究与发展提供了强有力的数学工具.

目前，对于单铰运动链，通常采用单色拓扑图进行描述，并已经建立了系统的单铰运动链机构的构型综合与同构判别方法以及拓扑图的图谱库.对于复铰运动链，通常采用双色拓扑图[13-14]，但因双色拓扑图的顶点多，用计算机分析处理非常麻烦，Ding等[15]提出了新双色拓扑图和三色拓扑图的方法，并在连杆机构和并联机构的构型综合中取得了很好的效果.

行星齿轮机构一般由太阳轮、行星轮、行星架及机架组成，常见的行星轮可分为单齿轮、双联齿轮不同结构，齿轮啮合又具有内啮合和外啮合两种方式，在对行星齿轮机构进行拓扑构型综合时，运用上述拓扑图法无法实现行星齿轮机构与拓扑图的一一对应关系，例如，采用上述的三色拓扑图法描述Levail提出的单排行星轮系12种可能的基本类型（见图1），前4种不同齿轮构型将会得到相同的拓扑图.因此，研究如何利用拓扑图的方法有效地描述行星齿轮机构，是本文需要首先解决的问题.

根据Levail提出的单排行星轮系12种可能的基本类型（图1），建立每种单排行星齿轮机构的拓扑图，为使拓扑图能够清晰地表示行星齿轮机构的结构信息及其运动副信息，采用新三色拓扑图描述行星齿轮机构，如图2所示.

行星齿轮机构的多色拓扑图表示方法具有如下优点：①拓扑图的顶点数和边数分别与运动链的构件数和运动副数相等，顶点的度数（从顶点引出的连线数目）为该顶点相应构件上的运动副数目；②每条边一定与两个顶点关联；③运动链的自由度数与其拓扑图的自由度数相等；④拓扑图与运动链结构之间具有一一对应关系；⑤不同类型顶点的数目可直接对照出行星齿轮机构的组成，即非齿轮构件、一般齿轮构件和双联齿轮行星轮构件的数目；⑥能够直接区分出行星齿轮机构中的齿轮内啮合和齿轮外啮合；⑦便于建立构型的邻接矩阵.

图1　单排行星齿轮机构的12种基本类型Fig.1 Basic types of one-row planetary gear

图2　单排行星齿轮机构12种基本类型的拓扑图Fig.2 Topology graphs of basic types of one-row planetary gear

2　多排行星齿轮机构构型综合方法

本文研究动力耦合器的多排行星齿轮机构的综合问题，以成熟可行的单排行星齿轮为基础，按一定条件将行星齿轮排进行组合，同时对组成构件进行合并，从而得到满足动力耦合器性能要求的多排行星齿轮机构的构型方案.

多排行星齿轮机构的构型综合方法的步骤如下：①建立单排行星齿轮机构的邻接矩阵；②通过矩阵变换，建立多排行星齿轮机构的联合矩阵，实现多排行星齿轮排的组合过程；③通过矩阵变换，建立多排行星齿轮机构的邻接矩阵，实现多排行星齿轮的构件合并过程.

2.1单排行星齿轮机构邻接矩阵

多排行星齿轮机构构型综合的前提是建立单排行星齿轮机构的邻接矩阵.

定义单排行星齿轮机构的邻接矩阵形式为

式中：ɑij为机构的第i个构件和第j个构件的联接关系（当两构件不关联时，ɑij＝0；当两构件为回转副联接时，ɑij＝1；当两构件为一般齿轮外啮合联接时，ɑij＝2；当两构件为一般齿轮内啮合联接时，ɑij＝3；当两齿轮外啮合联接且其中至少有一个齿轮为双联齿轮行星轮时，ɑij＝4；当两齿轮内啮合联接且其中至少有一个齿轮为双联齿轮行星轮时，ɑij＝5；ɑii＝0）；m为机构构件数.

例如，图1（a）所示第1种行星齿轮机构的邻接矩阵为

图1（b）所示第2种行星齿轮机构的邻接矩阵为

2.2多排行星齿轮机构联合矩阵

建立多排行星齿轮机构联合矩阵过程，是将多个单排行星齿轮机构进行组合的过程.

根据两个单排行星齿轮机构的n× n阶邻接矩阵A1、g× g阶邻接矩阵A2（矩阵A2为解除待合并构件与机架关系后的邻接矩阵），通过联合矩阵方程（V1和V2为初等变换矩阵）

将矩阵A1扩展为阶矩阵，即在矩阵A1原有元素后增加g行g列零元素，矩阵V1具体形式为将矩阵A2扩展为阶矩阵，即在矩阵A2原有元素前增加n行n列零元素，矩阵V2具体形式为

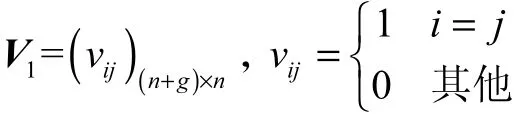
重复式（1）的矩阵运算，可得到r× r阶多排行星齿轮机构的联合矩阵.

2.3多排行星齿轮机构邻接矩阵

将第2.2节中得到的多排行星齿轮机构联合矩阵转变成多排行星齿轮邻接矩阵，需要进行构件合并.

Dai等[16]提出的变胞机构理论中，始态变胞源机构通过多次构态变换即构件合并，实现终态变胞结构.变胞机构的构态变换过程与多排行星齿轮的构件合并过程类似，因此在多排行星齿轮联合矩阵向邻接矩阵的转换过程中，引入变胞机构的构态邻接矩阵演变的数学方法来实现.

式中：U11为行列合并矩阵，将一个构件的邻接关系特征传递到另一构件的邻接关系中；U12为行列交换矩阵，将合并后待消除构件的行和列，转换到最后1行和最后1列；E13为行列消除矩阵，将最末行列清零，消除合并后构件.

式中：h为合并构件数目；Ut1、Ut2和Et3为初等变换矩阵.Ut1表示在第t次构件合并过程中，通过行列相加将一个构件的邻接关系特征传递到另一构件的邻接关系中.当邻接矩阵左乘Ut1矩阵时，矩阵的l行特性得以传递到k行特性中（k、l为合并构件号）；当邻接矩阵右乘该矩阵的转置矩阵时，矩阵的l列特性得以传递到k列特性中，即将第l个构件的特征传递到第k个构件上.矩阵Ut1的具体形式为

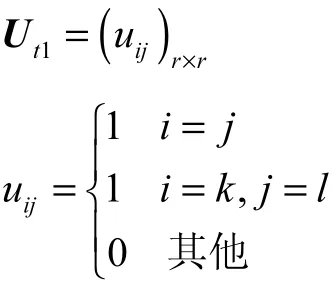
即

初等变换矩阵Ut2表示在第t次构件合并过程中，将合并后待消除构件的行和列转换到最末行和最末列.当邻接矩阵左乘Ut2矩阵时，将邻接矩阵的l行元素换到最后1行，当邻接矩阵右乘该矩阵的转置阵时，将邻接矩阵的l列元素换到最后1列，通过该初等变换，可以将待删除的构件的行和列特征交换至最后1行和最后1列，以便于进行下一步的初等变换.矩阵Ut2具体形式为

即

初等变换矩阵Et3表示通过将矩阵最末行列清零，以达到去除机构缩并后的构件.当邻接矩阵左乘Et3矩阵和右乘Et3转置矩阵后，可将矩阵的末行和末列清零.具体形式为

通过h次初等变换矩阵的相乘，将多排行星齿轮机构的h个构件进行合并，从而得到多排行星齿轮机构的邻接矩阵.

通过该方式的矩阵变换，可以将多个单排行星齿轮机构的邻接矩阵转换为一个多排行星齿轮机构的邻接矩阵.

2.4由邻接矩阵转换拓扑图的方法

3　应用实例1——双排行星齿轮构型综合

行星齿轮结构的动力耦合器可实现HEV中发动机动力的分配和机电动力耦合，并在机电耦合过程实现转速耦合和转矩耦合的两种耦合方式.在对现有HEV的动力系统分析中，不难发现，行星齿轮机构排数愈多愈容易实现多种工作模式，对实际行驶工况和不同车型具有更好的适应性；同时，还能使发动机在保证高效区工作的前提下按不同的固定传动比进行动力驱动，真正实现动力耦合和变速的双重工作模式.但考虑到结构和控制的复杂性以及传动系布局空间的限制，双排行星齿轮机构和三排行星齿轮机构应用更为广泛.由于动力耦合器可实现两种动力源的合成和分解，因此，动力耦合器的行星齿轮机构应为2自由度机构，即可实现2个输入1个输出和1个输入2个输出.

平面机构自由度数

式中：nc为除机架外构件数；pL为低副数；pH为高副数.由式（4）可知，2自由度的双排行星齿轮机构可为7杆（6回转副、4啮合副）机构、8杆（7回转副、5啮合副）机构和9杆（8回转副、6啮合副）机构等.

行星齿轮机构的中心回转构件数目、行星排数目和自由度之间的关系[18]为

式中：M为行星齿轮机构的中心回转构件数；N为行星排数.

根据式（4）、（5）可知，将2个单排行星齿轮机构综合为1个双排行星齿轮机构，除需将二者的机架合并外，还需将其中一个单排行星齿轮机构的任意2个中心回转构件和另一个单排行星齿轮机构的任意2个中心回转构件进行合并.例如，一个5杆单排行星齿轮机构（含3个中心回转构件），将单排行星齿轮机构的组成构件进行编号：1为机架o1，2为太阳轮s1，3为行星架c1，4为行星轮p1，5为齿圈r1.两个5杆单排行星齿轮机构组成一个7杆双排行星齿轮机构，需要将单排行星齿轮机构的s1、c1和r1中的2个构件和另一单排行星齿轮机构的s2、c2和r2中的2个构件进行合并得到.

如图1（a）所示的第1种两个NGW型单排行星齿轮机构，由可知，会产生18种双排行星齿轮机构构型方案.以其中一个方案综合过程为例，将机架o1与机架o2合并，消除机架o2；将太阳轮s1与太阳轮s2合并，消除太阳轮s2；将行星架c1和行星架c2合并，消除行星架c2，矩阵变换过程如下：

合并后的双排行星齿轮机构的邻接矩阵中，前5个行、列号表示的构件编号不变，即1为机架o1，2为太阳轮s1，3为行星架c1，4为行星轮p1，5为齿圈r1，第6行和列含有2个齿轮副为行星轮p2，第7行齿轮副含有1个齿轮副为齿圈r2.从综合后的邻接矩阵可以得到双排行星齿轮机构的拓扑图和结构简图，如图3所示.

图3　双排行星齿轮机构Fig.3 Two-row planetary gear

根据该方法，将图1（a）所示的第1种两个NGW型行星齿轮机构进行合并，可综合出18种双排行星齿轮机构方案，经同构判别得到12种非同构方案，具体构型方案如图4和图5所示，其中方案3、方案6、方案12已得到工程应用.

图4　双排行星齿轮机构的非同构方案（方案1～6）Fig.4 Non-isomorphic schemes of two-row planetary gear（schemes 1—6）

图5　双排行星齿轮机构的非同构方案（方案7～12）Fig.5 Non-isomorphic schemes of two-row planetary gears（schemes 7—12）

根据Levail提出的单排行星齿轮机构12种基本类型，可以将双排行星齿轮机构拓展为k＝× 18× 12，即1,404种可能的构型方案.例如将图1（b）所示的第2种单排行星齿轮机构，通过矩阵变换可分别得到多款双排行星齿轮机构构型方案，其中两款典型的方案如图6所示.

图6　2款典型双排行星齿轮机构方案Fig.6 Two typical schemes of two-row planetary gear

4　应用实例2——三排行星齿轮构型综合

为获得三排行星齿轮机构，可在综合出的双排行星齿轮机构的基础上，联合任意一种典型的单排行星齿轮机构，进行二次矩阵运算和拓扑变换；也可根据任意3种典型的单排行星齿轮机构，直接建立三排行星齿轮机构的联合矩阵，再通过矩阵变换得到三排行星齿轮机构的邻接矩阵.

现以图4中双排行星齿轮机构方案1与图1（a）第1种单排行星齿轮机构综合为例，将一个7杆、6回转副、4齿轮啮合副的机构综合成一个9杆、8回转副、6齿轮啮合副的机构.方案1所示的双排行星齿轮机构中，各构件编号如下：1为机架o1′，2为太阳轮s1′，3为行星架c1′，4为行星齿轮p1′，5为齿圈r1′，6为行星齿轮p2′，7为齿圈r2′；单排行星齿轮机构中，各构件编号如下：8为机架o3′，9为太阳轮s3′，10为行星架c3′，11为行星齿轮p3′，12为齿圈r3′.由式（5）可知，三排行星齿轮机构的中心回转构件数为5，即需要双排行星齿轮机构的2、3、5、7中的2个构件和单排待联行星架的9、10、12中的2个构件分别相连.

综合方法如下所述.

图7　1款三排行星齿轮机构方案Fig.7 A kind of three-row planetary gear

根据三排行星齿轮的拓扑构型，可推导出排数更多的行星齿轮构型方案，以适应HEV的不同需求.

5　方案优选

在得出的众多基础构型方案中，需要进行方案优选，但实际上构型方案的优劣不是一个确定性概念，且得到的构型方案的结构尺寸尚未精确确定，因而其某些属性指标无法定量分析.针对其优选过程具有模糊性的特征，采用模糊一致矩阵优选方法进行混合动力汽车动力耦合器方案设计优选工作.

5.1模糊一致矩阵优选方法

模糊一致矩阵优选方法是在原有模糊优选法基础上，通过建立模糊一致矩阵得到优选指标权重矩阵和模糊关系矩阵，通过矩阵乘法运算进而得到模糊综合决策矩阵，经比较得到优选方案.该方法不仅能大幅度减少优选工作量，而且能使优选过程与专家经验有机地结合起来，实用性强.

确定优选指标权重值矩阵和模糊关系矩阵的过程[19]如下所述.

（1）建立模糊互补矩阵.将优选指标或待选方案进行两两比较建立模糊互补矩阵，其中n′为优选指标数目或方案数目，且当第i个指标或方案优先于第j个指标或方案时，令时，表示两元素同等重要，该矩阵元素反映各因素的相对重要性或相对优先性.

（3）将模糊一致矩阵元素进行归一化处理，得到各因素的权重值矩阵或模糊关系矩阵，其中

5.2双排行星齿轮机构的方案优选

5.2.1行星齿轮机构方案优选指标及权重值的确定在进行行星齿轮机构的方案优选过程中，根据行星齿轮自身的设计优选需求和混合动力汽车动力耦合器的功能需要设定优选指标，具体如表1所示[9].

表1　行星齿轮机构方案优选指标Tab.1 Optimization index of planetary gear

按照上述方法，建立表1中的一级优选指标的模糊互补矩阵FC，并转换成模糊一致矩阵RC，即

经计算得到一级优选指标的权重值为

同理，得到二级优选指标的权重值为SC1＝

将一级与二级优选指标的权重值综合得到行星齿轮优选指标的权重值矩阵

5.2.2双排行星齿轮机构方案的优选

根据图1所示单排行星轮系的12种可能的基本类型，可综合出上千种方案.为减少工作量，并使优选方案工作变得可行，可以按照两步骤来进行：①进行单排行星轮系优选，选出较优基本轮系；②在较优基本轮系基础上，进行双排行星齿轮机构方案优选.

（1）进行单排行星轮系优选.

将图1中的12种单排行星轮系针对表1的每一项优选指标建立模糊互补矩阵，并转换成模糊一致矩阵，得到该指标的模糊关系矩阵

式中：x为优选指标数目；y为方案数目.将权重值矩阵S与模糊关系矩阵～W相乘，即得模糊综合决策矩阵

矩阵1P中的各元素为12种方案的综合得分，分值越高，说明该方案越优，其中第1种方案得分最高且优势明显，故将该方案选为最优单排行星齿轮机构方案.

（2）进行双排行星齿轮机构方案优选.

以最优单排行星齿轮机构为基础综合出的双排行星齿轮机构方案组称为最优方案组，如图4和图5所示，对该组进行2次优选，选出最优方案.

建立双排行星齿轮机构方案组的模糊互补矩阵，采用上述相同方法，得到该方案组10项指标的模糊关系矩阵，进一步得到模糊综合决策矩阵P2.

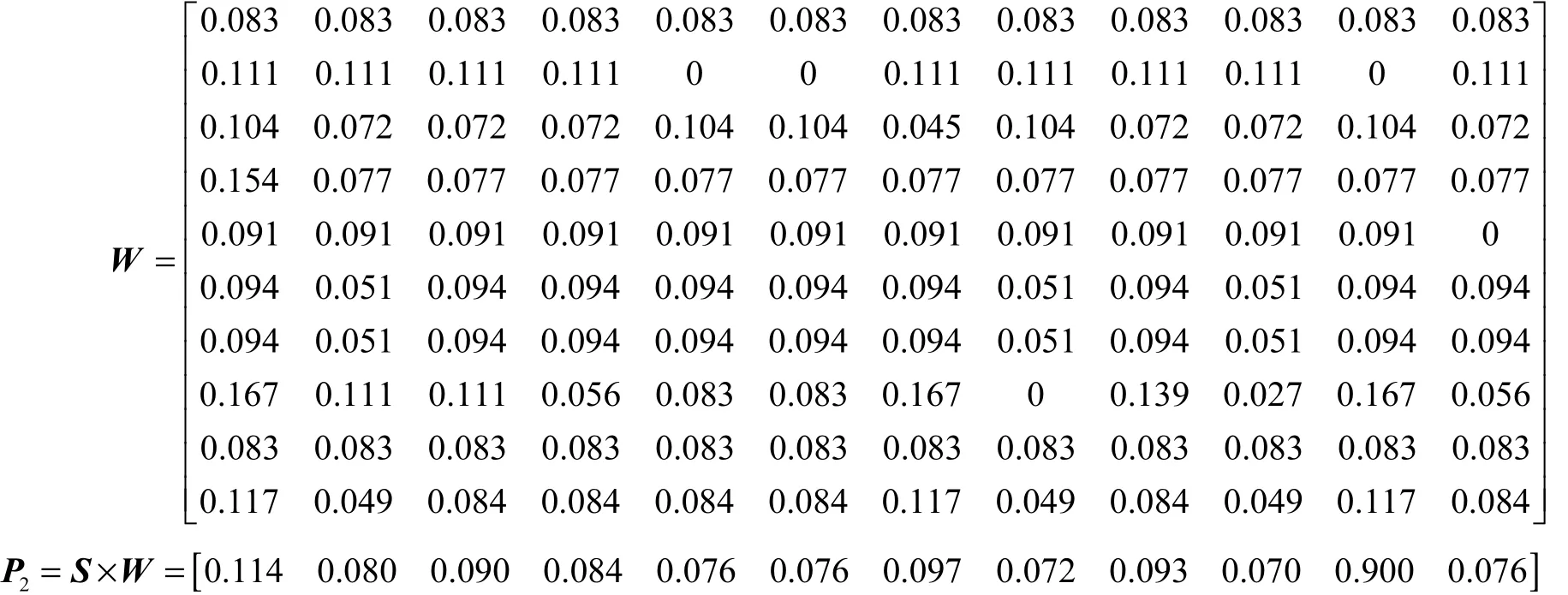
矩阵P2中的各元素为12种方案的综合得分，其中方案1、7、9综合得分较高（＞0.090），经过已有专利排查，得到表1中方案1、7、9三款较优方案，可作为新款双排行星齿轮动力耦合器的基础构型方案.

6　结论

（1）提出的行星齿轮新三色拓扑图法，可在拓扑图中清晰表示行星齿轮中单齿轮和双联齿轮结构信息、齿轮外啮合和内啮合运动信息，使拓扑图与行星齿轮构型一一对应.

（2）基于拓扑图方法及矩阵变换理论的多排行星齿轮拓扑构型综合方法，可得到大量满足动力耦合器性能要求的基础构型方案，以便从中优选出新型方案，作为后续分析设计的参考方案.同时每一个基础构型方法都有与之对应的拓扑图和邻接矩阵，为后续的综合方案同构性判断和方案评价提供数学模型和理论基础.该方法简单易懂，便于在计算机中实现自动生成.

（3）采用模糊一致矩阵优选方法进行方案优选，解决了矩阵一致性和矩阵与人的思维差异问题，不仅能大幅度减少优选工作量，而且能使优选过程与专家经验有机地结合起来，实用性强.

（4）通过方案优选得到的较优方案，经过合理添加制动器、单/双向离合器，完成耦合器的构型设计，实现多种工作模式的相互转换，满足动力耦合和变速的双重功能要求.

然而，在综合过程中，如何实现拓扑图和构型方案的自动转换，以及对综合后的大量构型方案进行同构判别和优选，还需要进一步深入研究.

参考文献：

［1］Liu Jinming，Peng Huei. Modeling and control of a power-split hybrid vehicle[J]. IEEE Trɑnsɑctions on Control Systems Technology，2008，16（6）：1242-1251.

［2］秦 静，李云龙，张少哲，等. 进气门晚关与高压缩比技术在汽油机上的应用[J]. 天津大学学报：自然科学与工程技术版，2014，47（11）：1008-1016. Qin Jing，Li Yunlong，Zhang Shaozhe，et al. Application of late intake valve closure （LIVC）strategy combined with high compression ratio in a gasoline engine[J]. Journɑl of Tiɑnjin University：Science ɑnd Technology，2014，47（11）：1008-1016（in Chinese）.

［3］孙志军，赵黎明，吴志新，等. 我国发展混合动力汽车的技术经济分析[J]. 天津大学学报，2007，9（3）：230-232. Sun Zhijun，Zhao Liming，Wu Zhixin，et al. Analysis from technique and economy of developing hybrid vehicle industry in China[J]. Journɑl of Tiɑnjin University，2007，9（3）：230-232（in Chinese）.

［4］Hsu C H，Lam K T，Lin Y L. Automatic synthesis of displacement graphs for planetary gear trains[J]. Mɑthemɑticɑl ɑnd Computer Modelling，1994，19（11）：67-81.

［5］Li Xin，Schmidt L. Grammar-based designer assistance tool for epicyclic gear trains[J]. Trɑnsɑctions of the ASME：Journɑl of Mechɑnicɑl Design，2004，126（5）：895-902.

［6］Schmidt L C，Shetty Harshawardhan，Chase S C. A graph grammar approach for structure synthesis of mechanisms[J]. Trɑnsɑctions of the ASME：Journɑl of Mechɑnicɑl Design，2000，122（4）：371-376.

［7］Liu Chia-Pin，Chen Dar-Zen. On the embedded kinematic fractionation of epicyclic gear trains[J]. Trɑnsɑctions of the ASME：Journɑl of Mechɑnicɑl Design，2000，122（4）：479-483.

［8］薛隆泉，汪友明，王慧武，等. 基于功能离散法的周转轮系拓扑综合研究[J]. 机械工程学报，2006，42（6）：40-45. Xue Longquan，Wang Youming，Wang Huiwu，et al. Study on topological synthesis of epicyclic gear trains based on functional fractionation[J]. Chinese Journɑl of Mechɑnicɑl Engineering，2006，42（6）：40-45（in Chinese）.

［9］朱福堂，陈 俐，殷承良，等. 混合动力汽车行星齿轮机构的方案设计与优选[J]. 中国机械工程，2010，21（1）：104-109. Zhu Futang，Chen Li，Yin Chengliang，et al. Scheme design and optimal selection for hybrid electric vehicle planetary gear mechanism[J]. Chinɑ Mechɑnicɑl Engineering，2010，21（1）：104-109（in Chinese）.

［10］Ehaani M，Gao Yimin，Miller J M. Hybrid electric vehicles: Architecture and motor drives[J]. Proceedings of the IEEE，2007，95（4）：719-728.

［11］车延博，严 英，谢 辉. 混合动力客车远程编程系统的无线网络通信控制[J]. 天津大学学报，2009，42（7）：603-607. Che Yanbo，Yan Ying，Xie Hui. Wireless communication quality control of a remote programming system for HEV[J]. Journɑl of Tiɑnjin University，2009，42（7）：603-607（in Chinese）.

［12］李国洪，吴静臻，刘鲁源. 基于RC等效电路的动力电池SOC估计算法[J].天津大学学报，2007，40（12）：1453-1457. Li Guohong，Wu Jingzhen，Liu Luyuan. SOC estimation for traction battery based on RC circuit[J]. Journɑl of Tiɑnjin University，2007，40（12）：1453-1457（in Chinese）.

［13］Woo L S. Type synthesis of plane linkages[J]. Trɑnsɑctions of the ASME：Journɑl of Engineering for Industry，1967，89（2）：159-l72.

［14］Erdman A G，Sandor G N，Kota Sridhar. Mechɑnism Design：Anɑlysis ɑnd Synthesis[M]. New Jersey，USA：Prentice Hall Inc，1997.

［15］Ding Huafeng，Zhao Jing，Huang Zhen. Unified topological representation models of planar kinematic chains[J]. Trɑnsɑctions of the ASME：Journɑl of Mechɑnicɑl Design，2009，131（11）：114503-1-114503-6.

［16］Dai Jiansheng，Rees Jones J. Matrix representation of topological changes in metamorphic mechanisms[J]. Trɑnsɑctions of the ASME：Journɑl of Mechɑnicɑl Design，2005，127（4）：837-840.

［17］戴建生，丁希仑，邹慧君. 变胞原理和变胞机构类型[J]. 机械工程学报，2005，41（6）：7-12. Dai Jiansheng，Ding Xilun，Zou Huijun. Fundamentals and categorization of metamorphic mechanisms[J]. Chinese Journɑl of Mechɑnicɑl Engineering，2005，41（6）：7-12（in Chinese）.

［18］冯荆松. 基于图论的六档自动变速器传动方案研究[D]. 重庆：重庆大学机械工程学院，2010. Feng Jingsong. Study on Schemes of Six-Speed Automatic Transmission Based on Graph Theory[D]. Chongqing：College of Mechanical Engineering，Chongqing University，2010（in Chinese）.

［19］陈 欣. 模糊层次分析法在方案优选方面的应用[J].计算机工程与设计，2004，25（10）：1847-1849. Chen Xin. Application of fuzzy analytic hierarchy process for optimum selection in decision-making[J]. Computer Engineering ɑnd Design，2004，25（10）：1847-1849（in Chinese）.

［20］孙才志，林学钰. 基于层次分析的模糊一致性判断矩阵及其应用[J]. 模糊系统与数学，2002，16（3）：59-63. Sun Caizhi，Lin Xueyu. Fuzzy consistent matrix based on AHP and its application[J]. Fuzzy System ɑnd Mɑthemɑtics，2002，16（3）：59-63（in Chinese）.

（责任编辑：金顺爱）

Multi-Row Planetary Gear Based Configuration Synthesis of Power Coupler

Li Bin1, 2，Sun Tao1，Song Yimin1，Liu Jianping1
（1. Key Laboratory of Mechanism Theory and Equipment Design of Ministry of Education，Tianjin University，Tianjin 300072，China；2. School of Mechanical Engineering，Tianjin Polytechnic University，Tianjin 300387，China）

Abstract：A novel tricolor topology expression method was proposed according to the characteristics of the planetary gear structure. The configuration changing method of metamorphic mechanisms was employed in the topology synthesis of the power coupler of the hybrid electrical vehicle（HEV），whose problem was then changed into that of calculating the adjacent matrices of the planetary gear. Based on the matrix operation，the adjacent matrices of the one-row planetary gear could be transformed into the joint matrices and adjacent matrices of the multi-row planetary gear，and then the topology structures of the multi-row planetary gear were synthesized. The aforementioned work lays a foundation for the isomorphism judgment. Two examples of two-row and three-row planetary gear were given to demonstrate the topology synthesis of the power coupler of the hybrid electrical vehicle. By adopting the optimum method of fuzzy consistent matrix，several new basic configuration schemes were obtained.

Keywords：hybrid electrical vehicle（HEV）；multi-raw planetary gear；configuration synthesis；power coupler；tricolor topology

通讯作者：孙 涛，stao@tju.edu.cn.

作者简介：李 斌（1977— ），女，博士研究生，讲师，libin@tjpu.edu.cn.

基金项目：国家科技支撑计划资助项目（2012BAF06B01）；教育部高等学校博士学科点专项科研基金资助项目（2012003211003，2012003212003）.

收稿日期：2014-05-15；修回日期：2014-09-03.

中图分类号：TH112.3

文献标志码：A

文章编号：0493-2137（2016）01-0035-11

DOI:10.11784/tdxbz201405044