钢筋混凝土圆筒仓仓壁结构的地震反应分析

郭　欢，孙武强 ，于　洋，马　倩

(1.陕西工业职业技术学院土木工程学院，陕西 咸阳　712000；2.西安建筑科技大学，西安　710055；

3.西安航光仪器厂，西安　710119；4.内蒙古自治区通辽市财政局投资评审中心，内蒙古 通辽　028000；

5.陕西省建筑职工大学，西安　710068)



钢筋混凝土圆筒仓仓壁结构的地震反应分析

郭欢1，2，孙武强3，于洋4，马倩5

(1.陕西工业职业技术学院土木工程学院，陕西 咸阳712000；2.西安建筑科技大学，西安710055；

3.西安航光仪器厂，西安710119；4.内蒙古自治区通辽市财政局投资评审中心，内蒙古 通辽028000；

5.陕西省建筑职工大学，西安710068)

摘要：以实际工程为依托，采用有限元软件ANSYS对钢筋混凝土圆筒仓仓壁结构进行数值模拟。通过模态分析，得到了筒仓结构的自振频率和周期。在模态分析的基础上，采用时程分析法，输入TAFT地震波，对模型结构进行动力有限元分析，得出结构在地震作用下的顶点位移时程曲线，找出最大位移发生时刻，并绘制该时刻结构的整体应力、变形图。最后，考虑不同贮料工况，对结构在TAFT地震波作用下进行了地震反应分析，得到相应的结论,为同类结构的抗震设计提供理论依据。

关键词：钢筋混凝土结构；筒仓；地震反应；模态分析；时程分析

0概述

筒仓[1]被定义为贮存散装物料的仓库，如粮食、饲料等粒状和粉状物料以及焦炭、水泥、食盐、食糖等散装物料，是农业、矿业、建材、化工、电力等诸多领域中广泛应用的构筑物。在矿井地面生产系统、选煤厂、水泥厂等工业生产过程的流水生产工艺中，筒仓起到缓冲原料与中间物料、协调生产，配送等必不可少的重要作用。筒仓的类型众多，但目前应用最广泛的是钢筋混凝土圆筒仓,故本文将结合工程实例对钢筋混凝土圆筒仓仓壁进行地震反应分析。

1工程实例

本文以某矿区选煤厂煤仓为依托。本工程为钢筋混凝土圆筒仓，直径50 m，高度25 m；设计基础承台厚度1.5 m，宽度5.3 m，基础埋深0.6 m，抗震设防烈度为8度；设计基本地震加速度0.2 cm/s2，场地类别：Ⅱ类；仓壁为C40钢筋混凝土，采用HPB235级、HPB335级钢筋。

2钢筋混凝土筒仓仓壁有限元模型

2.1筒仓结构基本尺寸的确定——仓壁厚度t(mm)和贮料计算高度hn(m)

本文所研究的钢筋混凝土筒仓直径为50 m。直径大于15 m的圆形筒仓仓壁厚度应按抗裂计算确定，通过查阅相关资料，确定本圆仓的仓壁厚度为t=700 mm。

本工程贮料计算高度为筒仓高度，即hn=25 m。

2.2建模材料参数的确定

仓壁采用C40等级混凝土，C40混凝土弹性模量E=32 500 N/mm2，泊松比为0.167，密度为2 500 kg/m3；HPB235级钢筋弹性模量E=200 000 N/mm2，泊松比为0.3，密度为7 850 kg/m3，钢筋屈服强度为300 N/mm2。

2.3荷载的确定

本着ANSYS软件建模简单高效的原则，此工程仓壁为圆筒仓的主要模拟结构。在建模过程中，不考虑仓顶上部结构及漏斗的作用。为简化模型计算分析，荷载包括筒仓自重及仓壁主要承受的原煤侧向压力。

根据《钢筋混凝土筒仓规范》(GB50077-2003)[2]附录C 浅圆仓贮料压力计算公式可以得出仓壁上单位面积上的压力沿高度按线性分布，顶端煤压力为0 MPa,底端煤压力为0.046 151 129 24 MPa。

2.4筒仓有限元模型单元的确定

结合本课题分析，在综合考虑分析的精度、单元数和单元类型后，筒仓实体选用Solid65单元。而用SURF154表面效应单元模拟不同贮料工况。

2.5模型坐标系的确定

设置工作平面在总笛卡尔坐标系下进行，原点设置在基础顶面中心处，竖向为X坐标轴，2个水平方向为Y轴与Z轴，荷载的加载在单元坐标下进行。

综上，利用ANSYS软件具体建模，形成钢筋混凝土圆筒仓仓壁有限元模型(图1)。

图1　生成有限元模型图(35 119个单元)

3模态分析

模态分析用于确定设计结构的自振特性[3]，即结构的固有频率与振型， 为计算地震反应提供重要参数， 结构的自振特性是衡量结构质量和刚度是否匹配、刚度是否合理的重要指标。同时，对筒仓使用安全性的评价与日常维护有着重要的意义。ANSYS软件的模态分析是线性的，任何非线性特性，如塑性和接触单元，即使定义了也将被忽略掉。

我们对以上建立的有限元模型，通过路径sulution>analysis type>new analysis>modal进行模态分析，通过路径sulution>analysis type> analysis options选择block lanczos为模态提取方法，研究过程中，提取了前20阶振型；然后通过路径main menu>solution>solve>Current LS进行求解，在求解完成后，确保推出当前solution重新进入，进行设置模态扩展，再通过路径sulution>analysis type>expansionpass及sulution>analysis type>load step opts扩展20阶振型；最后，通过路径MainMenu>general postproc>read results>list得到各阶频率。这里取前4阶振型的频率和周期，如表1所示。

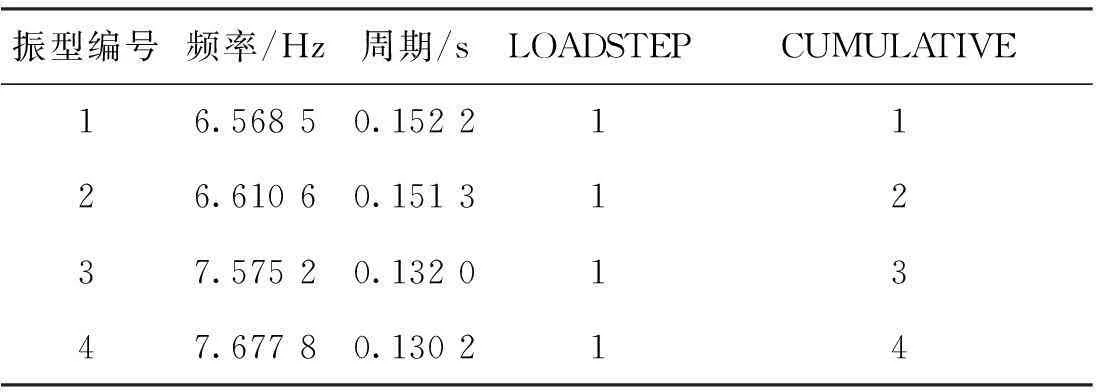
表1　结构前4阶振型固有频率、周期值

得到频率和周期后，通过路径MainMenu>general postproc>read results>plot得到结构前4阶振型图(图2)。

图2　前4阶段振型图(从左至右依次为第1、2、3、4阶模态振型)

从以上相关的图表数据分析可以得出以下结论：

1)从周期信息表可知结构的各周期均呈现2阶1组趋势，可定性地判断结构沿2个主轴方向质量和刚度分布均匀对称。

2)观察前几阶振型图可知，结构的固有频率首先出现在刚度较小的位置和方向， 1、2阶为X向两角突出，两角缩进；3、4阶为径向四角外扩,伴随X向四角突出，四角缩进。前4阶振型模态图未出现较明显扭转，较为理想。

3)筒仓高度为25 m，折算大约为9层建筑，筒仓第1自振周期T=0.152 2，参考同类高度的建筑，其第1周期偏小，频率较大，结构刚度较大。

4)从前4阶振型信息可知，在顶部开口处振动较为明显，实际工程中有环梁与顶盖的约束会适当减小，应该对此薄弱部位进行加强措施。筒仓结构的自振特性十分复杂，是一种以水平振动为主的结构形式。

4地震反应分析

4.1地震波的选取

我国《构筑物抗震设计规范》(GB50191-93)[4]采用时程分析法分析结构的地震反应时，应按建筑场地类别和设计地震分组,选用不少于2组的实际强震记录和1组人工模拟的加速度时程曲线。在研究时，我们采用了EL-CNENTRO波、TAFT波和1组时长30 s，峰值加速度达到970 cm/s2的人工强波。通过对分析结果的对比，发现TAFT波对结构的影响最大。故摘取TAFT波的地震反应分析成果,TAFT波记录时程曲线如图3所示。

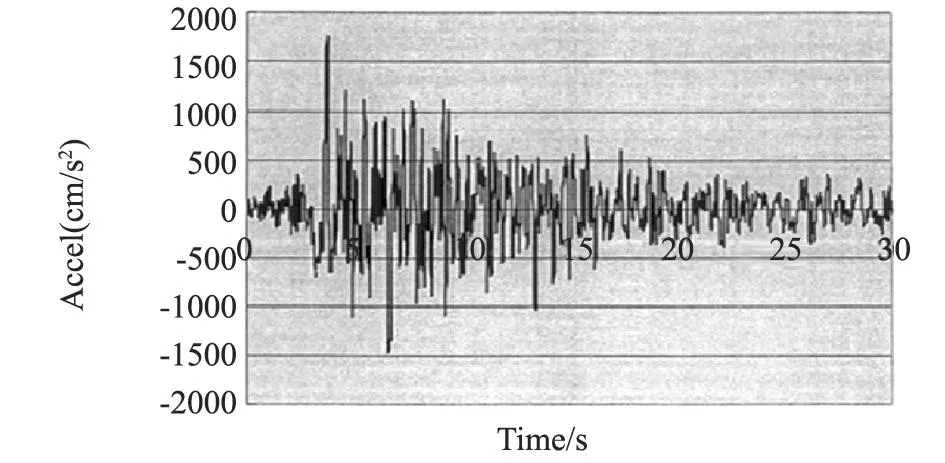
图3　TAFT波记录时程曲线

根据《建筑抗震设计规范》(50011-2010)[5]要求，采用时程分析法时，其加速度时程的最大值可采用表2数据。其中，括号内数值分别用于设计基本地震加速度为0.15 cm/s2和0.30 cm/s2的地区。

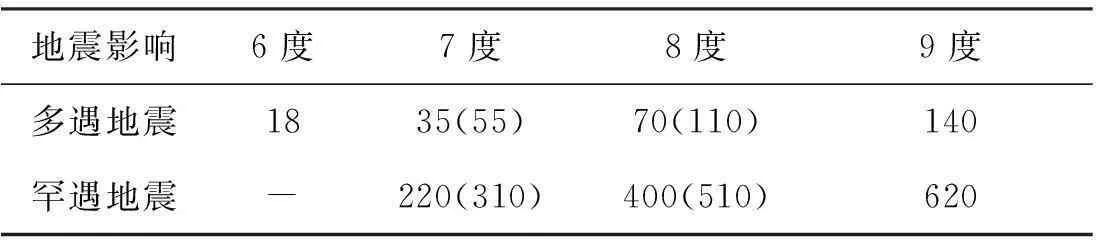
表2　时程分析所用地震加速度时程曲线的最大值　cm/s2

直接利用强震记录时，加速度峰值要调整到相当于设防烈度的规定值[6-7]，即用Ⅱ类场地土，设防烈度8度时的最大加速度除以地震波的最大峰值加速度，得到比例系数，再用比例系数乘以地震波各个时间点的加速度，即为实际要输入的地震波。

TAFT波的最大加速度aν,max=176.9 cm/s2，设防烈度为8度，多遇地震加速度时程曲线最大值为70 cm/s2，则计算如下：

所以，实际输入的多遇地震时的TAFT波应乘以0.4使用。同样方法，罕遇地震时的TAFT波调整为8度设防时罕遇地震的地震波。由于TAFT波出现峰值比较靠前，计算时选取前10 s的水平加速值输入。

4.2施加荷载及计算结果分析

1)TAFT波作用下,多、罕遇地震时结构的地震反应分析

继续采用前面建立的有限元模型，选择满载工况，采用相同的加载方式，分别导入调幅后的地震波，将地震波分别施加在结构上，分析结构的动力特性。

取TAFT波，制作ANSYS软件可读的txt的文档。文档中包含时间列与加速度列2列，时间间隔取0.02 s。在ANSYS中定义数组用命令流的形式将地震波加速度数组施加在总笛卡尔坐标下的Z方向，设置荷载步后进入计算，在时间历程后处理器中绘制出相应的时间位移曲线，在通用后处理器中显示出相应荷载步的位移、应力图。

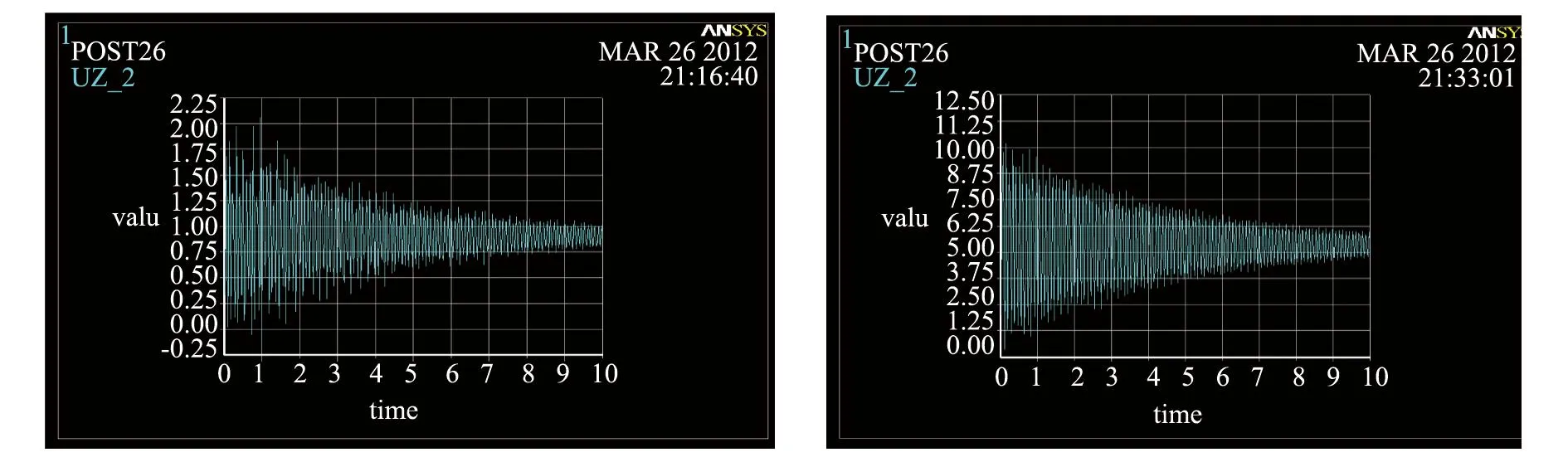
图4　调幅后多、罕遇地震时的TAFT波作用下654点位移时程曲线

图5　调幅后多、罕遇地震时的TAFT波作用下结构节点最大变形发生时结构Z向位移图

图6　调幅后多、罕遇地震时的TAFT波作用下结构节点最大变形发生时结构总位移图

在薄壁结构中，仓壁结构的变形情况依旧是主要问题，本文用节点最大总位移作为衡量仓壁结构功能的物理量。取有限元模型沿高度方向的最高点654点，绘出在调幅后地震波加速度作用下的时间位移曲线，讨论筒仓结构的地震反应。不同加速度作用下的2种654点时间位移图，如图4所示。由图4中看出在多遇地震时，TAFT波作用下654点即定点的位移极值为1 mm,发生时刻为1 s；罕遇地震时的位移极值为10.083 mm，发生时刻为0.14 s。同时说明结构的刚度很大，结构的变形满足规范要求的H/880。 在地震波的响应过程中，仓顶节点的位移变形在不同的地震波下有显著的差异，但是在相同波不同地震影响下的变形曲线规律基本一致。从图5和图6所示的位移云图可知，显示出红色的部位即位移极值部位，位于沿地震波施加方向结构的1/3高度处。由此可判断,地震作用下此部位为结构的薄弱部位，建议设计时适当加强。此外，在结构开口处位移相对大，分析原因是由于简化计算模型所致，在实际应用中，此处有环梁与顶盖的作用，位移会减小。

图7　调幅后多、罕遇地震时的TAFT波作用下结构节点最大变形发生时结构Z向应力图

分析图7可以得出：

①TAFT波作用下，红色黄色区域承受最大拉应力，应力最大值出现的部位与变形最大值出现的部位基本上一致，为地震作用下结构的薄弱部位，在地震波施加方向沿筒仓高度的1/3处。应力最大值分别为1.599 MPa、 1.715 MPa，低于混凝土抗拉强度设计值1.74 MPa。同时，罕遇地震下TAFT波在开口处应力较大。

②在3种地震波中，TAFT波对结构变形影响最大，说明TAFT波与结构自振周期较接近，容易引起共振效应，产生的侧移较大。

2)TAFT波作用下不同工况时结构的地震反应分析

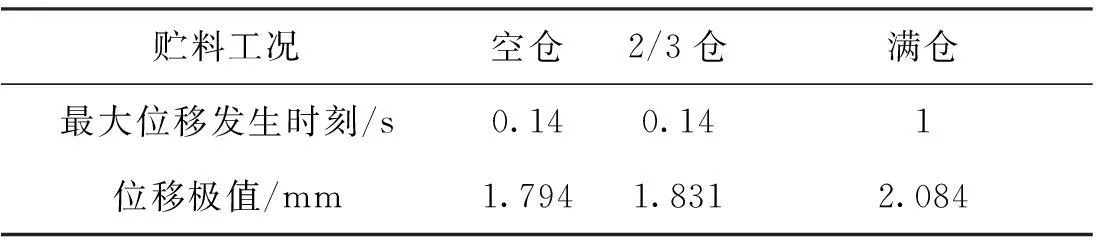
分析在多遇地震时TAFT波的作用下不同工况对结构的影响，得出顶点位移时程曲线图(图8)，并结合图8绘制出考虑不同工况下的地震作用(表3)。

图8　顶点位移时程曲线(从左至右依次为空仓、2/3仓、满仓时顶点位移时程曲线)

图9　顶点Z向位移图(从左至右依次为空仓、2/3仓、满仓时顶点Z向位移图)

贮料工况空仓2/3仓满仓最大位移发生时刻/s0.140.141位移极值/mm1.7941.8312.084

由以上图表(图8～9，表3)可知：

①在不同工况作用下，输入同一条地震波加速度幅值所得出的位移时程曲线形状是一致的，只是在顶点最大位移发生时刻与位移极值存在差别；

②空仓与2/3仓工况下极值发生时刻为0.14 s，满仓时为1 s，满仓相对前2种工况发生时刻滞后，说明仓内堆料质量对结构的地震响应产生一定影响，较多堆料质量参与地震动使位移极值发生时刻滞后，起到了一定的时刻延缓作用；

③ 3种工况下，Z向的最大位移均发生在地震波施加方向的仓壁边缘红色、黄色区域，随着贮料计算高度的升高，产生最大位移区域面积逐渐增大，沿着边缘处红色区域向下弥散至黄色区域位置，此位置为结构薄弱位置，满仓时产生位移最大为2.084 mm，空仓时产生侧移最小1.794 mm。

图10　顶点Z向应力云图(从左至右依次为空仓、2/3仓、满仓时的顶点Z向应力图)

根据表3找出顶点最大变形发生时刻，绘制出顶点最大变形发生时，不同工况作用结构的应力云图(图10)。从图10中可以得出：

①顶点变形发生最大时刻时，空仓结构所受最大压应力为0.289 625 MPa，最大拉应力为0.290 319 MPa；2/3仓时结构所受最大压应力为0.310 253 MPa，最大拉应力为0.327 098 MPa；满仓时结构所受最大压应力为0.466 163 MPa，最大拉应力为0.958 652 MPa。

②通过3种工况的变形对比，满仓时变形最大，空仓的变形最小，贮料对浅圆仓的作用在地震力下有一定的影响。但由于散料质量影响动力性能，散粒体材料是筒仓结构中贮存的主要材料，它既不同于连续固体，又不同于连续流体，在震动中将呈现相当复杂的运动性态，并对筒仓结构的本体产生复杂的动力相互作用，给筒仓结构的动力特性带来很大的影响。要想确定结构在地震作用下是否为控制工况，还需要与实际实验相结合。

③在红色黄色区域承受最大拉应力，蓝色区域承受最大压应力，应力最大值出现的部位与变形最大值出现的部位基本上一致，为地震作用下结构的薄弱部位，在地震波施加方向沿筒仓高度的1/3处。在今后设计中对显示较弱部位进行加强，可以使结构受力更加合理和安全。

5结论

1)对筒仓仓壁结构的有限元模型进行模态分析表明：前4阶振型图均属于水平振动，结构以水平振动为主；结构的第一周期偏小，刚度偏大；结构沿2个主轴方向质量和刚度分布均匀对称，未出现较明显的扭转效应。

2)选取TAFT地震波，采用时程分析法对模拟结构的地震反应进行研究，得出结构顶点位移时程曲线。通过分析得出：在地震波的响应过程中，TAFT波对结构变形影响最大，说明TAFT波与结构自振周期较接近，容易引起共振效应，产生的侧移较大。

3)通过TAFT地震波作用下空仓、2/3仓、满仓3种工况的变形对比可知：贮料储存量一定程度上会影响浅圆仓的地震反应。另外，筒仓主要贮存煤等散体材料，其质量会影响动力性能，且在地震中运动性态不规律，与筒仓结构的本体还会产生复杂的动力相互作用，从而影响筒仓结构的动力特性。

4)在地震作用下，沿筒仓高度的1/3处应力与变形出现了最大值，为结构的薄弱部位，应加强设计。

参考文献：

[1]金立兵, 许启铿, 王录民. 钢筋混凝土立筒仓动力性能研究现状与展望[J]. 河南工业大学学报: 自然科学版, 2010, 31(1): 84-87, 94.

[2]中华人民共和国建设部. GB 50077-2003, 钢筋混凝土筒仓设计规范[S]. 北京: 中国计划出版社, 2004.

[3]小飒工作室. 最新经典Ansys及Workbench教程[M]. 北京: 电子工业出版社, 2004.

[4]中华人民共和国建设部. GB 50191-1993, 构筑物抗震设计规范[S]. 北京: 中国标准出版社, 1995.

[5]中华人民共和国建设部. GB 50011-2010, 建筑抗震设计规范[S]. 北京: 中国建筑工业出版社, 2010.

[6]赵晶, 李建亮, 何玉林, 等. 现行中国烈度表的修订研讨[J]. 华北地震科学, 2014, 32(3): 35-38, 49.

[7]李建亮, 李福海, 亢川川, 等. 地震动输入界面处剪切波速对加速度峰值的影响[J]. 华北地震科学, 2015, 33(1): 5-10.

Seismic Response Analysis of Reinforced Concreat Cylindrical Silo Wall Stucture

GUO Huan1,2，SUN Wu-qiang3，YU Yang4，MA Qian5

(1. Civil Engineering Department of Shaanxi Polytechnic Institute, Xianyang 712000, China;2. Xi'an University of Architecture and Technology, Xi'an 710055, China;3. Xi 'an navigation optical instrument factory, Xi'an 710119, China;4.Investment Review Center of Tongliao Bureau of Finance, Tongliao 028000, China;5.Architecture Zabor University of Shaanxi Province, Xi'an 710068, China)

Abstract:In his study, we took practical engineering as the basis, used the finite element software Ansys to make numerical simulation for the structure of reinforced concrete cylindrical silo wall and carries. Through the Modal Analysis, weobtained the silo structure's natural frequency and cycle.On the basis of Modal Analysis, weused the time history method, input TAFT earthquake wave ,carried on the dynamical finite element analysis to the model structure,obtained the crown of the structure displacement time interval curve under earthquake function, discovered the time at which the biggest displacement occurred,and drew up the whole structure stress chart and the whole structure distortion chart in this time. At last,according to different stores-material operating mode,the study analzed the earthquake response of the structure under the TAFT earthquake wave function, also obtained the corresponding conclusion.Thestudy can provide theoretical basis for the seismic design of similar structures.

Key words:reinforced concrete structure; silo; seismic response; numerical simulation modal analysis; time history analysis

doi:10.3969/j.issn.1003-1375.2016.01.009

中图分类号:P315.923

文献标志码:A

文章编号:1003-1375(2016)01-0053-07

作者简介：郭欢(1986—)，女，陕西延安人，陕西工业职业技术学院土木工程学院专职教师，西安建筑科技大学在读博士.E-mail:452930188@qq.com.

基金项目：国家自然科学基金项目 “建筑钢结构隐形损伤与磁记忆信号的量化关系”(51478383)

收稿日期:2015-08-21

郭欢，孙武强,于洋，等．钢筋混凝土圆筒仓仓壁结构的地震反应分析[J]．华北地震科学，2016，34(1)：53-58.