一种外环水平结构双轴光纤惯导系统旋转方案设计方法
唐江河,李文耀,詹双豪,刘东斌,赵 明
(北京自动化控制设备研究所,北京 100074)
一种外环水平结构双轴光纤惯导系统旋转方案设计方法
唐江河,李文耀,詹双豪,刘东斌,赵 明
(北京自动化控制设备研究所,北京 100074)
目前国内外长航时高精度自主惯导系统多采用双轴旋转调制自动补偿技术,而旋转方案设计对系统导航精度影响至关重要。双轴惯导系统按结构可分为外环水平结构和外环航向结构两类。分析了外环水平结构双轴惯导系统在旋转方案设计中的局限性,考虑到光纤陀螺输出特性,指出外环水平结构双轴光纤惯导系统不宜采用传统旋转方案,并提出了一种该类双轴光纤惯导系统的旋转方案设计方法,最后对所设计旋转方案与十六位置旋转方案进行试验对比,试验表明此设计方案导航精度提升了71%。
外环水平;双轴惯导系统;旋转调制;旋转方案;方案设计
0 引言
目前国内外长航时高精度自主惯导系统普遍采用旋转调制自动补偿技术,而旋转方案设计是自动补偿技术的一个重要研究方面。旋转方案直接影响惯导系统的导航精度,不同的旋转方案对系统的各种误差源的调制效果有很大的区别,因此必须从多方面对旋转方案进行分析,以设计合适的旋转方案。
双轴惯导系统按结构可分为外环水平和外环航向两类。两种结构有各自特点:外环水平结构利于系统参数标定,可进行系统全参数自标定,但不利于载体运动航向隔离,局限了旋转方案设计;外环航向结构不利于系统参数标定,不能进行系统全参数自标定,但便于载体运动航向隔离,方便旋转方案设计。
国内外双轴激光旋转惯导系统技术已较为成熟。激光陀螺具有标度因数稳定、输出受温度磁场影响较小等优点。而光纤陀螺具有可靠性高、无机抖装置,利于旋转机构控制,随机游走误差相对较小等优势。光纤陀螺和激光陀螺的不同特性,必然会导致惯导系统在进行旋转方案设计时的侧重点不同[1-2]。
本文分析了外环水平结构双轴光纤惯导系统的结构局限性,考虑到光纤陀螺的输出特性,提出外环水平结构双轴光纤惯导的一种旋转方案设计方法。
1 旋转方案介绍
1980年,Sperry公司用磁镜偏频激光陀螺研制了单轴旋转式惯导系统,系统采用四位置停转方案,四位置转动次序为:-135°、+45°、+135°、-45°,如图1所示。Sperry公司随后就开始机械抖动激光陀螺单轴旋转式惯导系统的研制,20世纪90年代研制了MK39 Mod3C单轴旋转系统和MK49双轴旋转系统,MK39 Mod3C系统采用单轴四位置停转转动方案,系统自主导航精度达到1n mile/24h。MK49系统采用双轴转动方案,定期使惯性敏感装置绕方位轴和横摇轴旋转,用来消除陀螺漂移和其他误差源,系统自主导航精度可达0.39n mile/30h,但具体旋转方案未在任何文献上有所提及。
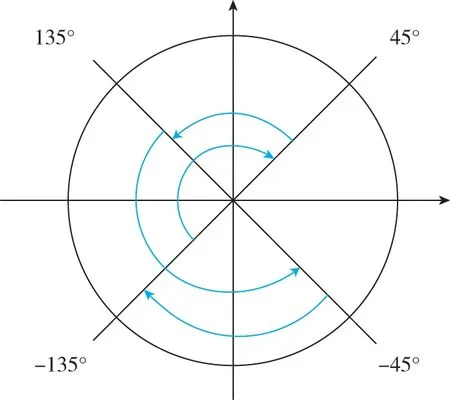
图1 单轴四位置转动方案Fig.1 Four-sequence rotation scheme of single-axis rotary SINS
国内对旋转调制惯导系统旋转方案设计的研究较多。除图1所示方案外,单轴旋转惯导系统较有效并被普遍采用的是如图2所示的“正反反正”方案。也有方案为追求更好对称性,在90°和270°两个位置上有相应停留,但设计思路和目的都是一致的:有效调制与旋转轴指向垂直的陀螺零偏、加速度计零偏、陀螺安装误差以及加速度计安装误差,同时也有效消除了旋转轴方向陀螺标度因数误差由于系统自身旋转引起的导航误差。文献[3-5]指出载体机动对旋转调制惯导系统的调制效果有很大影响,假想一种极为特殊状况,载体只存在角运动,并且角运动与系统旋转轴的旋转角运动正好相互抵消,那么系统IMU坐标系和地理坐标系始终保持不变,此时旋转惯导系统相当于一个捷联惯导系统,不再具有自动补偿功能。有鉴于此,文献[5]提出了隔离载体运动的旋转方案,即系统旋转机构在执行预先设计的旋转方案的同时反向叠加载体的航向机动,以抵消载体角运动对旋转调制影响。
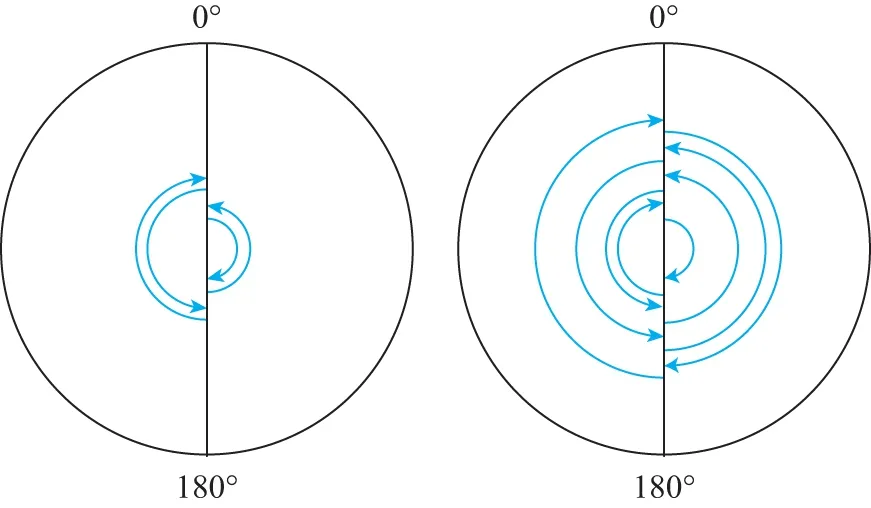
图2 常用单轴旋转方案Fig.2 Usual rotation scheme of single-axis rotary SINS
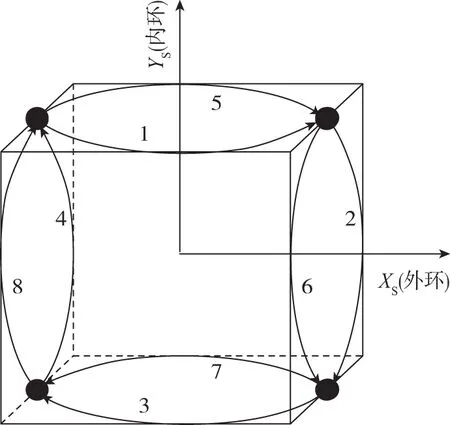
图3 八位置双轴旋转方案示意图Fig.3 Eight-sequence double axis rotary schematic diagram
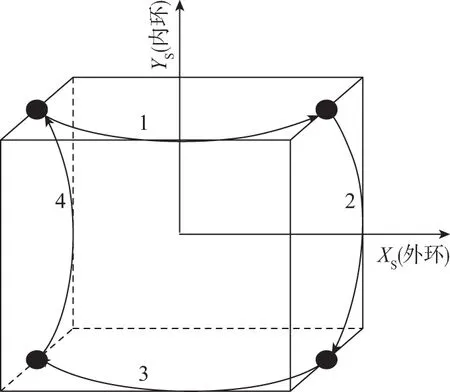
(a)
(b)
(c)

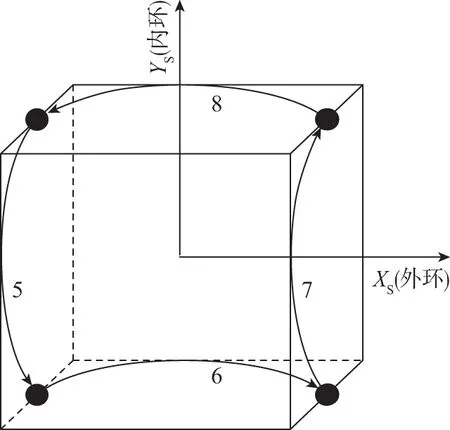
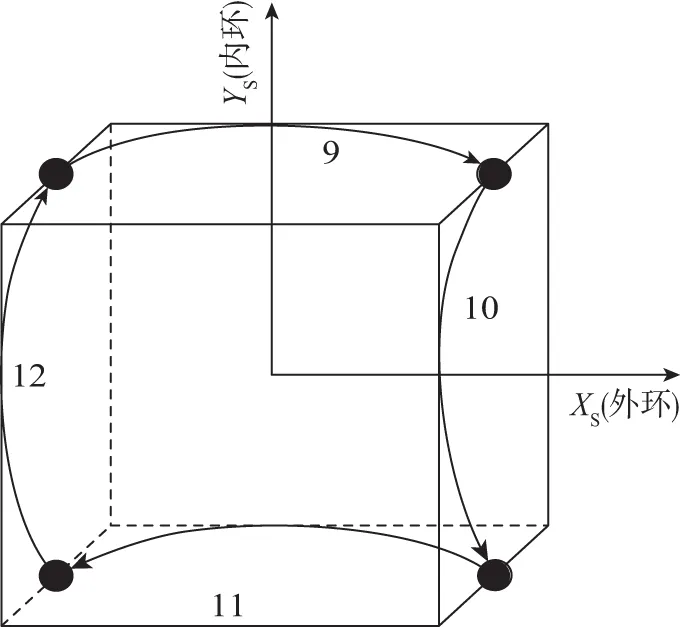
(d)图4 十六位置双轴旋转方案示意图Fig.4 Sixteen-sequence double axis rotary schematic diagram
该方案可以很好地调制安装误差和标度因数误差,但对陀螺标度因数不对称性没有补偿效果。为此,文献[6]改进该旋转方案,得到如图4所示十六位置方案,该方案在失调角层面不仅调制了陀螺和加速度计的零偏、标度因数以及安装误差,同时陀螺标度因数不对称性也得到很好的调制效果。文中进一步提出在十六位置方案的每一步旋转的中点(即90°或270°)增加一个位置,实现三十二位置旋转方案。该三十二位置旋转方案和十六位置旋转方案的调制效果是一样的,只是它能更好地压制旋转惯导系统“锯齿波”幅值。
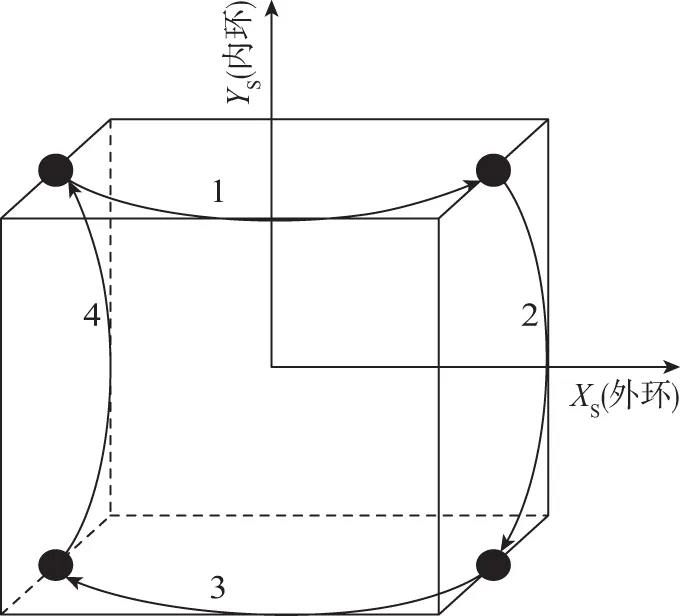
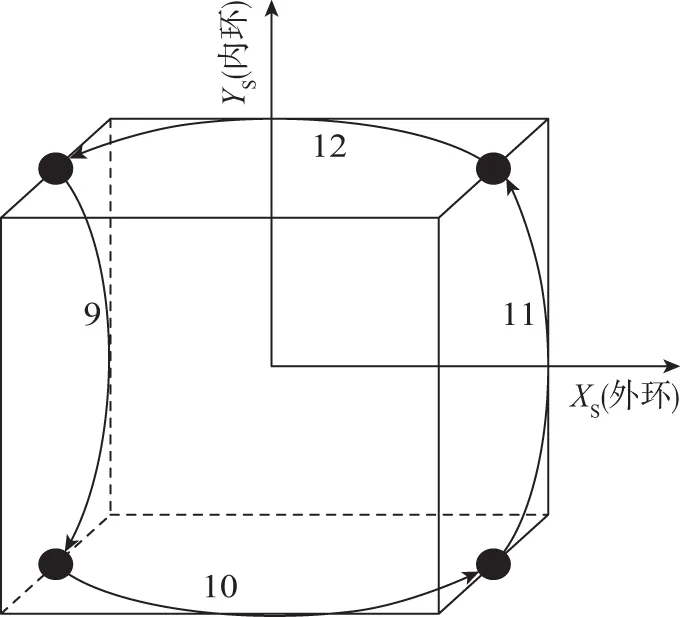
这两种旋转方案虽然在系统失调角层面具有很好的调制效果。但在速度层面该旋转方案的调制效果有限,尤其是陀螺安装误差会引起系统速度误差的增长。为此,文献[7]对十六位置旋转方案进行了改进,有效提高了系统速度层面的调制效果,其旋转方案示意图如图5所示。
(a)

(b)
(c)
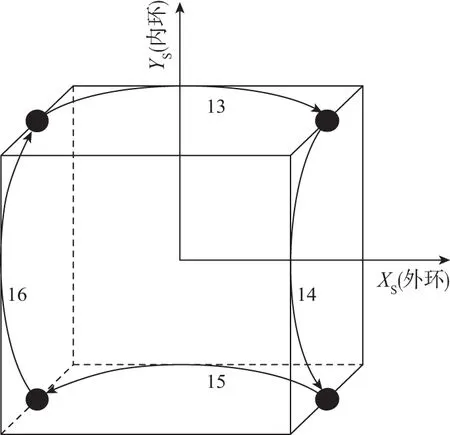
(d)图5 改进十六位置双轴旋转方案示意图Fig.5 Modified sixteen-sequence dual-axis rotary schematic diagram
以上提及的一系列旋转方案,不适合在外环水平结构双轴光纤惯导系统上应用。一方面,如第4节所分析的,该种结构的双轴惯导由于结构限制,将无法解耦标度因数误差和系统航向之间的耦合作用,而以上旋转方案中,外环的频繁翻转,容易引起系统水平失调角的积累;另一方面,相比于激光陀螺,光纤陀螺标度因数稳定性和温度敏感性较差,更易引起失调角的积累[8]。
2 坐标系定义
涉及的坐标系定义如下:
惯性坐标系(i):原点与地球质心重合,Xi轴沿地球转轴指向地球北极,Yi轴和Zi轴在赤道平面内,不随地球旋转,且Zi轴和初始时刻当地东向重合。
地理坐标系(g):定义为北天东坐标系。
台体坐标系(p):利用3个加速度计的敏感轴方向OXa、OYa、OZa进行定义,X加速度计的敏感轴方向OXa即为Xp、Yp在OXaYa所在平面内,且与OXa垂直;Zp与Xp、Yp满足右手定律。
惯导坐标系(b):当惯导的2个环架都锁定为0时,台体坐标系即为惯导坐标系。
3 双轴光纤惯导系统导航误差模型
为了便于分析,导航坐标系选为惯性坐标系,利用形式相对简单的Ψ方程进行分析。
(1)
式中:
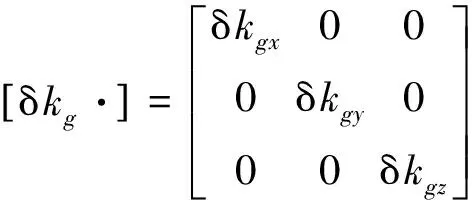
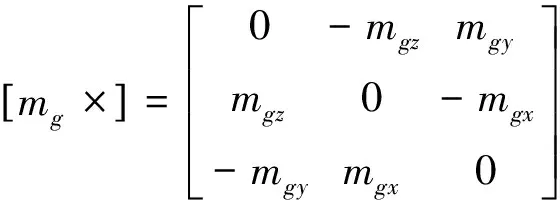

其中:ε0为陀螺漂移误差;
δkg为标度因数误差;
mg为陀螺安装误差;
ng为陀螺安装的不正交度。
忽略重力加速度相关误差后,其速度误差方程可表示为
(2)
注意式(2)中旋转激励项为第二和第三项,因此仅分析一个旋转周期短时间内各种误差源对速度误差的影响时可将式(2)进一步简化为
(3)
那么经简化后系统的姿态和速度误差的解为:
(4)
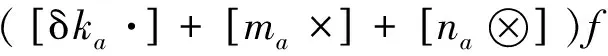
(5)
其中:δa0为加速度计零偏;
δka为加速度计标度因数误差;
ma为加速度计安装误差;
na为加速度计安装的不正交度。
有:
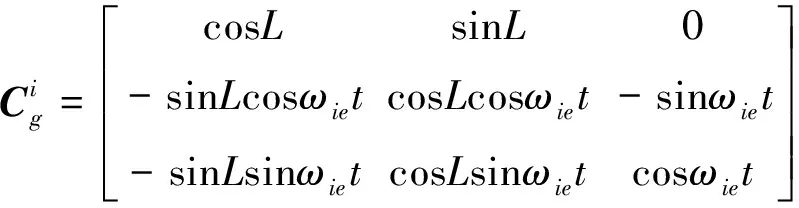
式中:L为当地纬度;
ωie为地速数值;
roll、pitch和yaw分别为基座坐标系相对于地理坐标系的滚动、俯仰和航向;
α和β分别为旋转机构外环和内环的旋转角度;
ω1和ω2分别为外环和内环的旋转角速率。
(6)
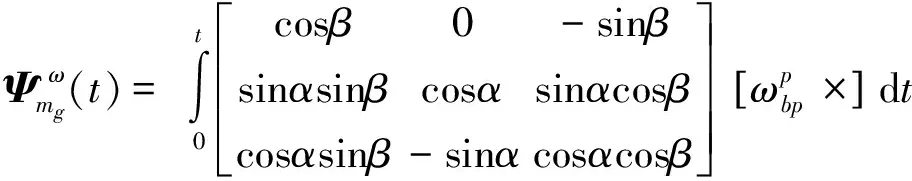
(7)
(8)
其中,Ψωδkg、Ψωmg、Ψωng分别为陀螺标度因数误差、陀螺安装误差以及陀螺安装不正交度由于系统自身旋转导致的系统失调角误差的系数矩阵,即Ψωδkg、Ψωmg、Ψωng分别与陀螺标度因数误差、陀螺安装误差以及陀螺安装不正交度的误差矢量相乘,可得到各自引起的失调角矢量大小。
4 外环水平双轴惯导系统旋转方案设计局限性
外环水平双轴惯导系统在外环翻转时容易引起较大水平失调角,严重影响导航误差。旋转方案一般设计思路是布局多个适当外环翻转进行相互抵消,避免水平失调角的快速累积。然而,由于外环水平结构的双轴惯导系统的结构特点,当载体航向发生变化时,由于陀螺标度因数误差、陀螺安装误差及安装不正交度与系统航向之间的耦合作用[5,9],将无法完全避免水平失调角累积。以改进十六位置旋转方案为例,说明外环翻转时外环水平结构对方案设计的局限性。
提取出改进十六位置中2,4,5,7,9,11,14,16几个外环翻转过程,描述如表1所示。

表1 改进十六位置中外环翻转过程
旋转描述中前括号为翻转前外环和内环角度,后括号为翻转后外环和内环角度。而箭头上符号表示正向或负向翻转。
为简化分析,在一个旋转周期内,只考虑载体航向机动,忽略俯仰和滚动机动,并忽略载体移动距离。
以下分两种情况讨论,当航向变化时,陀螺标度因数、陀螺安装误差及陀螺安装不正交度对系统失调角的影响。
4.1 系统不隔离载体机动
将第i次翻转引起的失调角投影到地理坐标系上(其中忽略了惯性系相对于地理坐标系的变化)。
陀螺标度因数引起的失调角为
陀螺安装误差引起的失调角为
陀螺不正交度引起的失调角为
则有:
1)如果旋转周期内,载体航向不变,标度因数、安装误差以及安装不正交度不引起系统失调角积累;
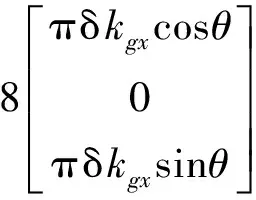
假设陀螺标度因数误差为1.5×10-5,旋转周期为10min,该情况下系统将在水平面北偏东θ的方位上产生77.76″的失调角,相当于系统在此方位上存在一个0.130(°)/h的等效陀螺漂移。
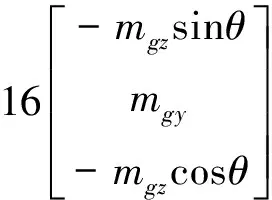
假设陀螺安装误差或不正交度为5″,旋转周期为10min,该情况下系统将在水平面东偏北θ的方位上产生80″的失调角,相当于系统在此方位上存在一个0.133(°)/h的等效陀螺漂移。
4.2 系统隔离载体机动
隔离载体的理想目的是不管载体如何机动,应满足以下两个条件:
1)系统失调角应与航向角θ无关且为0:
考虑到δkG、mG和nG以及航向角θ的任意性,要满足以上三式与航向角无关,必须要求:
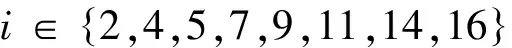
2)每个外环旋转过程中,外环旋转的角度α初始和终止时的角度应满足表1,而旋转的角度应满足
可以证明有以下结论:
1)陀螺标度因数误差无法通过隔离载体机动获得理想的调制效果;
2)只需构造一种旋转方式满足以下条件,即可使得陀螺安装误差或安装不正交度通过隔离载体机动获得理想调制效果。
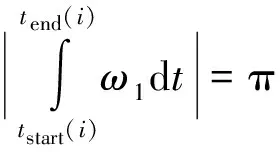
内环的旋转角度为反对称的:β(t)=-β(Ts-t)(Ts为外环翻转过程时间);
综合以上结论可知,系统在进行外环翻转时,陀螺标度因数误差与系统航向的耦合作用无法解耦;而陀螺安装误差和安装不正交度与系统航向的耦合作用可以通过适当的隔离策略得到解耦。
这表明双轴激光惯导系统由于陀螺标度因数稳定性好,采用改进十六位置旋转方案可以获得较好的导航精度,但双轴光纤惯导系统由于光纤陀螺标度因数稳定性差,不宜采用这类旋转方案。
5 双轴光纤惯导系统旋转方案的设计
由上面的分析可知,由于光纤陀螺标度因数稳定性较差,旋转方案设计时应尽量减少外环轴的翻转;另一方面,为减小天向陀螺漂移对系统精度的影响,外环轴的翻转又不能过少。双轴光纤惯导系统旋转方案设计如图6所示。系统第一次外环翻转的时间为T,之后每隔时间2T外环翻转一次,对应的隔离方案采用4.2节构造的策略;系统其余时间采用内环单轴旋转方案,对应的隔离方案采用文献[5]或文献[10]中提到的方法;在方案设计中还有两个关键环节需要确定。
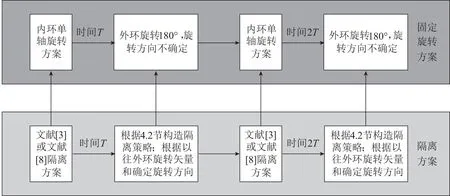
图6 双轴光纤惯导系统旋转方案Fig.6 Rotary scheme of dual-axis FOG INS
5.1 外环旋转方向的确定
4.2节中构造的跟踪策略对外环旋转方向没有具体要求,而这为增强陀螺标度因数误差调制效果提供了可能。根据以往外环旋转矢量在水平面上投影的矢量和确定外环旋转方向。
5.2 时间T的确定
依以上分析,时间T须根据几个主要技术指标确定:陀螺标度因数稳定性、陀螺零偏稳定性以及系统工作时间。
以实际陀螺精度指标为例来进行设计说明:陀螺标度因数稳定性1.5×10-5;陀螺零偏稳定性0.02(°)/h(100s平均);系统工作时间为8h。
计算当陀螺标度因数稳定性为1.5×10-5,8h系统导航最大误差随时间T的变化曲线如图7中红线所示。计算当陀螺零偏稳定性为0.02(°)/h,8h系统导航最大误差随时间T的变化曲线如图7中蓝线所示。

图7 最大导航位置误差随时间T的变化曲线Fig.7 Curve of maximum position error with time T
由两曲线可以确定最优翻转时间T约为100min。
6 车载试验验证
为了验证该旋转方案的有效性,利用一套双轴光纤惯导系统进行了车载验证试验,系统用光纤陀螺精度同5.2节。试验主要对比了旋转方案一(图5所示的十六位置旋转方案)和旋转方案二(图6所示的旋转方案)两种旋转方案。
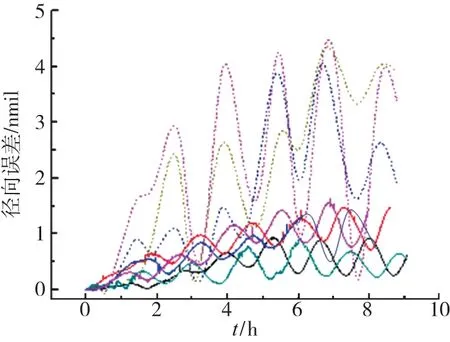
图8 导航位置误差对比曲线Fig.8 Comparison curve of position error
试验时,双轴惯导系统固定于实验车上,准备时间和准备流程都一致,时间为30min,完成了初始对准以及一些主要误差参数的标定,对准完成后,车辆开动,行驶路线任意。为验证充分,方案一和方案二分别进行了3次和5次试验。8次试验的导航径向误差曲线如图8所示,虚线所示为方案一的3次试验位置误差曲线,实线所示为方案二的5次试验位置误差曲线。图8中显示,方案二最大位置误差不超过1.6n mile,而方案一最大位置误差都超过了4.2n mile。表2对8次试验位置误差的TRMS(True Root-Mean-Square,位置精度)值进行了处理。表2中序号1~5的5次试验为方案二试验,序号6~8的3次试验为方案一试验。由表可知,方案二的TRMS均值为0.67n mile,而方案一的TRMS均值为2.32n mile,精度提升了71.3%(=(2.32-0.67)/2.32)。

表2 导航位置误差的TRMS值
7 结论
文中指出外环水平结构对旋转方案设计具有局限性,无法解耦陀螺标度因数误差与系统航向之间的耦合。而光纤陀螺标度因数稳定性较差,不宜采用传统旋转方案。为此,在解决以下三点的基础上提出了一种外环水平结构双轴光纤惯导系统的旋转方案设计方法:给出解耦陀螺安装误差和安装不正交度的隔离策略;由外环旋转矢量和最小原则确定外环旋转方向;由陀螺标度因数稳定性、零偏稳定性及导航时间确定外环翻转间隔时间。
所设计旋转方案具有良好导航精度。试验证明,30min准备时间,导航8h,TRMS达到0.67n mile,相对十六位置旋转方案提升71%。
[1] Lefevre H C. The fiber-optic gyroscope: actually better than the ring-laser gyroscope [C]//OFS2012 22nd International Conference on Optical Fiber Sensor. International Society for Optics and Photonics, 2012.
[2] Divakaruni S, Keith G, Narayanan C, et al. Strategic Interferometric Fiber-Optic Gyroscope for Ballistic Missile Inertial Guidance[C]// AIAA Guidance, Navigation and Control Conference and Exhibit,2008.
[3] 张伦东, 练军想, 胡小平. 载体角运动对旋转式惯导系统旋转调制效果的影响[J]. 国防科技大学学报, 2011, 33(4):152-156.
[4] 覃方君, 李安, 许江宁. 载体角运动对旋转调制惯导系统误差影响分析[J]. 武汉大学学报:信息科学版, 2012, 37(7):831-833.
[5] 许江宁, 查峰, 李京书,等. 单轴旋转惯导系统“航向耦合效应”分析与补偿[J]. 中国惯性技术学报, 2013,21(1):26-33.
[6] 李瑞涛, 吴修振, 周绍磊. 双轴旋转惯导系统转位方案仿真分析[J]. 导弹与航天运载技术, 2013(5):15-19.
[7] 纪志农, 刘冲, 蔡善军,等. 一种改进的双轴旋转惯导系统十六位置旋转调制方案[J]. 中国惯性技术学报, 2013,21(1):46-50.
[8] 徐海刚, 郭元江, 李志峰,等. 旋转调制光纤陀螺惯导寻北精度探索[J]. 导航定位与授时, 2015,3(2):11-15.
[9] 常国宾, 许江宁, 李安,等. 载体运动对双轴连续旋转调制式惯导方案误差的影响[J]. 中国惯性技术学报, 2011, 19(2):175-179.
[10] Levinson E, Ter Horst J, Willcocks M. The next generation marine inertial navigator is here now[C]// Position Location and Navigation Symposium. IEEE, 1994:121-127.
Rotation Scheme Design Method for Dual-Axis INS with Horizontal Outer-Axis Structure
TANG Jiang-he, LI Wen-yao, ZHAN Shuang-hao, LIU Dong-bin, ZHAO Ming
(Beijing Institute of Automatic Control Equipment, Beijing 100074, China)
The long endurance and high precision autonomous INS always adopt rotation modulation self-compensation technology, and its accuracy is significantly influnced by the rotation scheme design. According to the structure, dual-axis INS can be devided into two categories, horizental outer-axis and vertical outer-axis. Considering the limitation of dual-axis INS with horizental outer-axis structure and the output characteristics of the FOG, the paper pointed out that INS with horizental outer-axis is not suitable to the traditional rotation scheme and proposed a design method of rotation scheme for this kind of dual-axis INS. The result of experiment shows that the navigation precision with the proposed scheme increased by 71% compared with sixteen-squence scheme.
Horizontal outer-axis; Dual-axis INS; Rotation modulation; Rotation scheme; Scheme design
10.19306/j.cnki.2095-8110.2016.04.001
2016-01-10;
2016-05-25。
国家自然科学基金(41527803)
唐江河(1979-),男,博士,高级工程师,主要从事导航制导方面的研究。E-mail:Hittangjianghe@163.com
U666.12
A
2095-8110(2016)04-0001-08

