离散正交变换理论实例教学法的探索与实践
王建卫
(东北林业大学 机电工程学院,黑龙江 哈尔滨 150040)
离散正交变换理论实例教学法的探索与实践
王建卫
(东北林业大学 机电工程学院,黑龙江 哈尔滨 150040)
为了生动地讲解枯燥的正交变换公式,探讨了离散正交变换理论实例教学的重要性和具体实施方法.在教学环节中设计了2个典型的离散哈尔变换教学实例.在启发学生绘制一维哈尔变换的快速算法流程图基础上,完成二维哈尔变换的计算问题,能够让学生理解离散正交变换计算的关键所在,有助于帮助学生深入地理解正交变换理论.实践证明,离散正交变换理论的实例教学效果良好.
正交变换;离散哈尔变换;实例教学
目前大学所开设的主要数学课程包括高等数学、线性代数、概率论与数理统计、计算方法、复变函数与积分变换和离散数学等课程[1],矩阵变换作为一个较为独立的教学内容,在多门课程里都有不同程度的涉及.通常电子与信息类专业是以信号与信息处理作为主要的研究方向[2],信号的各种变换是以矩阵变换为基础的,因此,变换理论成为大学数学教学的重点内容是必然的.离散正交变换是矩阵变换的一种特殊形式,具有变换类型多,变换公式复杂,计算难度较大的特点,因此进行相应的教学方法探索是必要的[3].
典型的课堂教学方法有讨论式教学法[4]、问题式教学法[5]和实例教学法[6]等.讨论式教学法的核心是启发学生就特定问题发表自己的见解,以培养学生独立思考的能力和创新精神,适用于大学低年级的理论知识较浅的课程和高年级的应用类专业课程.问题式教学法的核心是以问题为导向充分发挥学生主观能动性,适用于具有一定知识基础的大学高年级的学生和设计类课程的课堂教学.实例教学法的核心是在教师指导下,根据课程教学目标和内容的需要,通过典型实例的分析和讲解完成教学,这一教学方法在许多学科的教学工作中取得了良好的效果,适用于大学较低年级的学生和理论性较强课程的课堂教学.
离散正交变换理论公式枯燥,难以理解,在授课过程中发现存在学生理解不够深刻,应用意识不强的问题.因此,本文以哈尔变换为例设计了2个典型的离散正交变换实例,对离散正交变换理论的实例法课堂教学进行了有益的探索与实践.
1 离散正交变换理论教学内容分析
在电子信息类专业高年级的专业课授课中发现,离散正交变换理论是大学数学的一个不容忽略的重点和难点内容.在课堂讲授过程中,必须进行特征向量变换、哈尔变换、沃尔什变换、哈达玛变换、斜变换和余弦变换等几种经典的离散正交变换理论公式的推导[7-8].在传统的以讲授理论为主的变换理论课堂教学中,由于变换理论教学内容的枯燥性,学生在听讲过程中会出现注意力不够集中、听不懂的情况,导致缺乏学习兴趣,学习效果不佳.
为了提高学生的学习兴趣,可以采用实例教学法进行授课.按照由浅入深、循序渐进的原则将离散正交变换理论的教学内容划分为离散正交变换的定义、变换矩阵及其性质、快速算法和实例分析等4个基本点.

在授课过程中通过引导学生分析正交变换的定义,得出了“正交矩阵是正交变换定义的核心”的结论,调动了学生独立思考新问题的积极性,也有助于培养学生的创新思维.
2 实例教学法在离散哈尔变换计算中的应用
在实例教学法的教学过程中,教师应精心选择把抽象理论转化到具体问题的实例,实例的选择是否恰当将直接影响到教学效果[9].好的实例应满足一般性、扩展性和启发性的要求,离散正交变换教学过程中选择实例的3个原则是:第一,选择的变换类型要符合一维和二维离散正交变换的一般定义;第二,二维正交变换计算过程可分解为2次一维正交变换的计算,因此快速计算流程实例以一维正交变换为主,并可扩展得到二维正交变换计算的规律;第三,总结二维离散正交变换的计算过程,通过数据的重排和编程实现启发学生思维,开拓计算思路,使实例具有普适性.根据这3个原则,离散正交变换理论的教学过程可分为教师讲授正交矩阵,师生共同给出正交变换的定义,学生绘制快速算法流程图并由教师规范作图和指出离散哈尔变换的应用背景等4个递进的环节.
以哈尔变换为例,介绍实例教学法在离散正交变换理论教学中的应用.
第1个环节是由教师讲授哈尔矩阵的形式.连续哈尔函数的数学解析式经过离散化后可得到哈尔矩阵,在讲解过程中,教师应注意对连续函数离散化的实质进行分析.
连续哈尔函数的定义(归一化)为

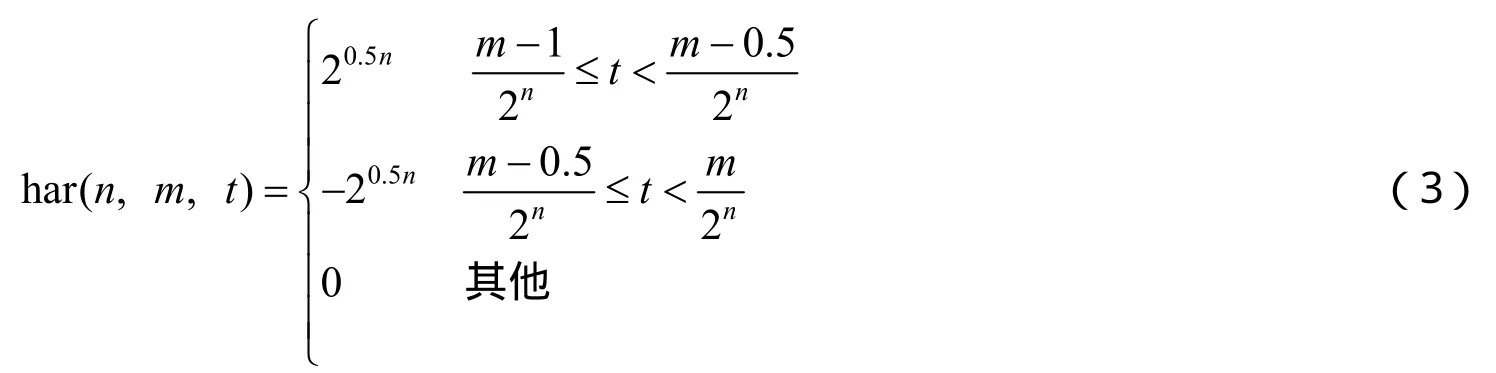
离散矩阵H(r)是由连续函数计算得到的,在讲解时注意(N为连续哈尔函数图形的取样次数),其中:r为包含0阶的总阶数.
第2个环节是由教师给出哈尔变换的形式.在给出哈尔变换形式的教学过程中,教师应分析一维哈尔变换、二维哈尔变换以及正、逆变换公式的区别.
对于N维向量XN,一维哈尔正变换的计算公式为

一维哈尔逆变换的计算公式为

在课堂教学中,通过分析矩阵数据的特点,参考一维变换的形式,部分学生能够较为准确地书写二维变换公式.
对于NN阶矩阵X,二维哈尔正变换的计算公式为

二维哈尔逆变换的计算公式为

分析式(4)~(7),师生共同总结出正变换矩阵不转置,二维变换是2次一维运算的规律,这有助于学生在有限的课堂时间内更稳固地记忆公式,提高了课堂学习效率,节省了课余的复习时间.
第3个环节是面对简单而内涵丰富的变换公式给出课前教师设计的实例,选择计算公式,引导学生自己画出快速算法流程图,由教师总结规律并规范作图.
例1 设计一维哈尔变换的快速算法流程图.
例1是典型的快速算法流程图的绘制问题,应从3个关键点进行详细分析和讲解.第1个关键点是由连续的哈尔函数确定矩阵H(2);第2个关键点是将变换的计算公式表示为代数表达式;第3个关键点是化简代数表达式.
由式(4)可知,当N4时,一阶哈尔正变换的计算公式为

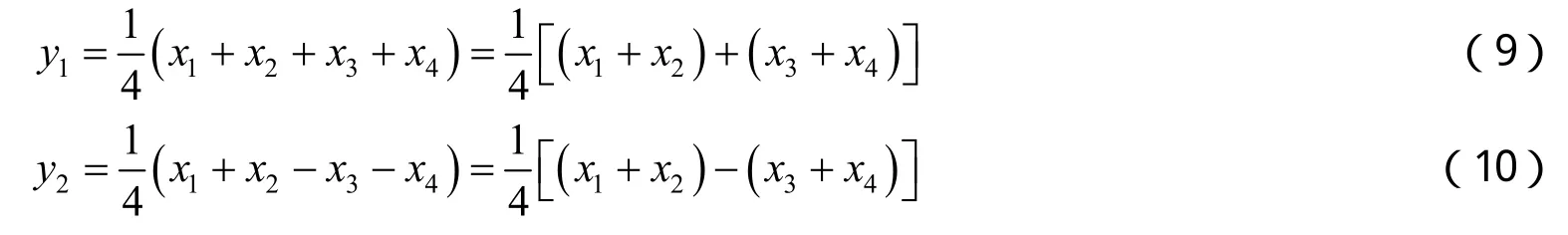
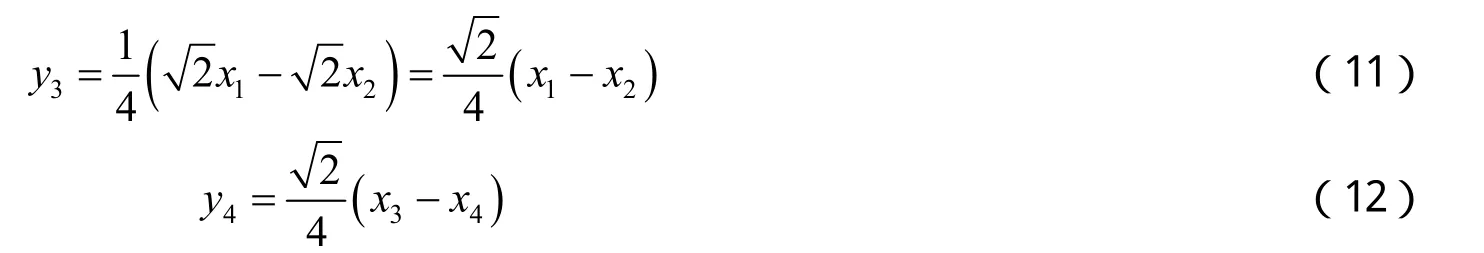
由式(9)~(12),按照由左至右、由上至下的原则教师板书绘制快速算法流程图(见图1).
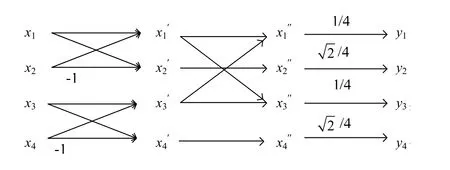
图1 一维哈尔正变换的快速算法流程图
参考一维哈尔正变换快速流程图,课堂上学生基本上能根据式(5)绘制出逆变换的快速算法流程图(见图2).

图2 一维哈尔逆变换的快速算法流程图
通过引导学生绘制一维哈尔变换的快速算法流程图,使哈尔变换的代数表达式成为简单的计算流程,基本要点是保存中间结果,避免重复运算,有助于帮助学生深入理解快速算法的实质,也激发了学生自己归纳其他变换类型相关问题的浓厚兴趣.考虑到课堂时间的有限性,把哈达玛变换的快速算法流程图作为作业,学生完成效果良好,这说明实例教学法在一定程度上能够激发学生的自学能力.
第4个环节是指出离散哈尔变换的应用背景.根据图像处理理论,矩阵中元素的排列位置是图像信号特征的表示形式之一,引导学生如何应用离散哈尔变换找到这些特征,通过计算找到矩阵的具体特征形式,最后给出课前设计并通过MATLAB代码实现的计算[10-11].
例2是典型的二维计算问题,应从4个关键点进行详细分析和讲解.
第1个关键点是将x分解为4个4×4的子矩阵.由于8阶的哈尔矩阵形式复杂,0数据可看作图像数据的边界,易出现书写和编程的错误,因此将x分解为4个4×4的子矩阵.用公式(6)计算是简单易行的方法,在课堂上让学生自主选择8×8或者4×4的哈尔矩阵完成计算,发现选择4×4形式的学生占多数,并且容易出现多种计算结果.
第2个关键点是通过编写MATLAB代码验证学生计算的正确性.此时应将矩阵按照从左至右、自上而下分为4个4×4的子矩阵.
数值计算的MATLAB代码:

第4个关键点是有效数字的选取.当符号计算的结果取5位有效数字时,与数值计算的结果相同.
通过分析和编程计算,使枯燥的二维哈尔变换计算跃然于屏幕上,极大地激发了学生的学习热情.建议学生通过修改例2的代码实现沃尔什变换和哈达玛变换等计算问题,在一定程度上也提高了学生通过编程完成计算的实际能力,取得了较好的教学效果.
3 结论
本文在分析讨论式教学法、问题式教学法和实例教学法基础上,选择实例教学法对离散正交变换理论教学过程的重要环节进行了归纳和总结,以哈尔变换为例详细叙述了授课中所做的讲解和分析.实践表明,实例教学法是一种有效、可行的课堂教学方法,可以帮助学生快速精准地记忆变换公式,让学生理解离散正交变换计算的关键所在,激发了学生自己归纳不同科目的数学理论,使之成为一个知识体系的浓厚兴趣,也为学生在高年级学习专业课程打下了坚实的基础,激发了学生的创新思维.
[1]王友国.大学数学课程体系和教学内容的改革与实践[J].数学教育学报,2010,19(4):88-91
[2]高凯,许云峰,张永强.电子信息类创新人才培养模式研究与实践[J].教育教学论坛,2011(1):232-232
[3]黄廷祝,高建.大学数学研究型教学方法和考试方法改革与实践[J].中国大学教学,2012(11):52-55
[4]杨春梅.关于讨论式教学法及其应用问题探究[J].教育探索,2014(1):62-63
[5]郭姣,刘艳良.问题式教学法在“信号与系统”课程教学中的运用[J].电气电子教学学报,2010,32(5):83-85
[6]余艳,邢远秀,刘燕丽.关系数据库范式理论的实例教学法探讨[J].高师理科学刊,2016,36(2):66-69
[7]胡茂林.矩阵计算与应用[M].北京:科学出版社,2008:268-305
[8]邱启荣,张可铭.矩阵论与数值分析基础[M].北京:中国电力出版社,2011:35-48
[9]李存金,张慧娇.创新思维方法在大学课程教学中的运用[J].教育与教学研究,2013,27(9):57-60
[10]王建卫,曲中水.MATLAB 7.X程序设计[M].北京:中国水利水电出版社,2007:67-185
[11]郑连存,张艳.培养学生科学思维和创新能力的研究与实践——谈大学数学研究型教学[J].大学数学,2014,30(2):43-47
Exploration and practice of the example teaching method of the discrete orthogonal transformation theory
WANG Jian-wei
(College of Mechanical and Electrical Engineering,Northeast Forest University,Harbin 150040,China)
In order to vividly explain the boring orthogonal transformation formulas,discusses the importance and concrete implementation methods of the example teaching about the discrete orthogonal transformation theory.The two typical teaching examples of discrete Haar transformation are designed in the teaching process.On the basis of inspiring the students to draw the flow chart of fast algorithm of the one-dimensional Haar transformation,the students respectively complete the calculation of the two-dimensional Haar transformation.It can make the students understand the key to the discrete orthogonal transform computation,helps the students understand the theory of the orthogonal transformation deeply.The practice has proved that the good teaching effects are obtained by the teaching method.
orthogonal transformation;discrete Haar transformation;example teaching
O151.21∶G642.0
A
10.3969/j.issn.1007-9831.2016.12.021
2016-09-22
王建卫(1973-),女,山东龙口人,副教授,博士,从事模式识别与智能系统研究.E-mail:jwwang2007@163.com
1007-9831(2016)12-0078-05

