基于X-12-ARIMA方法的武汉市空气污染指数波动分析*
俞 艳 胡兴帮# 任苏蕊 童 艳
(1.武汉理工大学资源与环境工程学院,湖北 武汉 430070;2.华东师范大学地理科学学院,上海 201100)
空气污染指数(API)是反映空气质量的重要指标[1],由SO2和NO2等污染物浓度及其持续时间确定。API受多种因素影响,如气候、降水量等,这些因素多具有时间变化特性,因此学者多采用时间序列分析方法对其进行研究。如周荣美等[2]利用统计分析的相关知识分析了杭州市萧山区“十一五”期间的空气质量变化及其影响因素;柴微涛等[3]通过建立ARMA模型对成都市API进行分析和预测;LEE等[4]运用季节ARIMA模型对马来西亚的API进行预测研究等。然而,这些研究大多基于统计分析或单一的ARIMA模型,由于多时点月均API受季节和历法效应的影响,不同月度或季度之间的数据较难反映空气污染变化的基本层面。因此,为了提高不同月度数据的可比性,进行季节调整是一种可取的方法。季节调整是把预调整时间序列中存在的季节性成分、历法效应剔除掉,调整后的时间序列只包含趋势成分和不规则成分。第一个被广泛应用的季节调整方法是由SHISKIN等[5]于1965年开发的X-11方法,后来逐步完善,形成标准的X-11方法,利用滑动平均来估计趋势成分和季节成分。但由于时间序列两端存在非对称权重问题,常导致成分估计与实际存在较大差异。1988年X-11方法与BOX等[6]的ARIMA模型相结合以延长时间序列,较好地解决了对称权重问题。1995年又引入RegARIMA模型对其进行改进,季节调整之前可对时间序列中存在的异常值和历法效应做预调整。经过实践和修改,1998年FINDLEY等[7]在X-11方法的基础上引入预调整模块,正式推出X-12-ARIMA方法及配套程序,该方法在社会经济等时间序列的季节调整分析中应用较广泛。
针对API时间序列常呈现出的趋势性及季节性特点,本研究尝试采用X-12-ARIMA方法对API时间序列数据进行分析,并以武汉市作为研究对象,将其2001—2012年API时间序列分解成3种成分(趋势成分(Tt)、季节成分(St)和不规则成分(It)),以探索武汉市API的波动规律,进而为武汉市空气质量的改善提供科学基础。
1 基于X-12-ARIMA模型的API
X-12-ARIMA模型包括X-11与RegARIMA两个模块。X-11方法是基于移动平均的季节调整算法,它将时间序列分解成3种成分。RegARIMA模块主要用来修正和剔除各类离群值、假日等因素的影响,对时间序列进行前向和后向的扩展,以保证在使用移动平均进行季节调整的过程中数据的完整性。
本研究将X-12-ARIMA模型引入API时间序列分析,构建了API的X-12-ARIMA模型。首先引入预调整模块RegARIMA,通过建立带有回归元的ARIMA模型对API时间序列中存在的各种离群值和历法效应做预调整,并对经过预调整时间序列进行前向和后向预测,对时间序列进行扩展。然后,将预调整后的API时间序列回归误差导入X-11模块进行季节调整,应用多次迭代的移动平均方法将时间序列分解成3种成分[8]140。RegARIMA的形式可表示为:
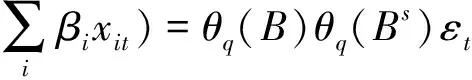
(1)
式中:φp(B)、θq(B)分别为非季节性p阶自回归算子、q阶移动平均算子;Φp(Bs)、θq(Bs)分别为季节性P阶、Q阶移动平均算子;B为延迟算子;s为季节周期的长度(月度为12,季度为4);d、D分别为非季节性、季节性差分阶数;Yt为API月度调整时间序列;i为回归项序号;βi为第i个回归系数;xit为回归变量,一般包括离群值和历法效应等;εt为白噪声序列。
式(1)通常用Box-Jenkins记法表示成(pdq)(PDQ)s。序列分解模型一般有加法分解模型和乘法分解模型[9]。API变动分析的具体流程见图1,其中赤池信息量(AIC)/贝叶斯信息量(SBC)准则参考文献[10]。
2 基于X-12-ARIMA方法的武汉市API变动规律分析
2.1 样本选取与数据预处理
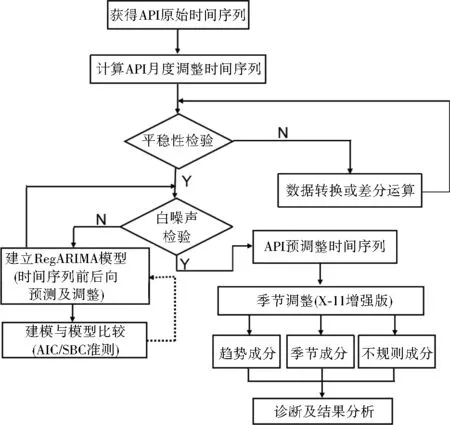
图1 基于X-12-ARIMA模型的API时间序列分析流程Fig.1 API sequence analysis flow chart based on the X-12-ARIMA model
武汉市是湖北省的政治、经济和文化中心,位于江汉平原东缘、汉江及长江交汇处,是全国重要的工业基地和交通通信枢纽。近年来,随着复兴大武汉进程的不断加快,武汉市作为长江中游城市群的重要组成部分,其空气质量状况备受人们关注,对其变动规律的探索研究也显得愈发重要。
由于武汉市环境保护局自2013年1月1日起正式以空气质量指数(AQI)替代原有的API表征空气质量状况,本研究依据2001年年初至2012年年底环境保护部发布的API日报数据进行武汉市API的变动规律分析。对于数据缺失项,以其前后2天平均值进行插补。最终,计算整理得到武汉市2001年1月至2012年12月共计144项API原始时间序列数据。
2.2 基于ARIMA模型的API时间序列延伸
原始API为日报数据,按月对日报数据进行简单平均得到API月度数据,由于月度数据并不依赖于该月的星期构成,不存在交易日效应,故X-12-ARIMA模型无需对交易日效应进行调整。但由于X-12-ARIMA模型根据美国日历而设定,不能对中国由于阴历与阳历差异产生的移动假日效应进行直接处理。故本研究对春节、清明、端午和中秋等法定假日进行历法效应调整[8]141,剔除历法效应后的API月度调整时间序列见图2。
首先,需建立ARIMA模型以完成API时间序列的延伸。图2显示,API月度调整时间序列具有逐年下降的趋势性以及较明显的季节变动。考虑到该序列方差不稳定,需要预先对月度调整时间序列进行数据转换(见式(2))和差分运算(采用一阶十二步差分(见式(3))),得到差分后时间序列(见图3)。图3表明,差分后时间序列在均值0上下随机波动。差分后时间序列平稳性检验结果如表1所示。
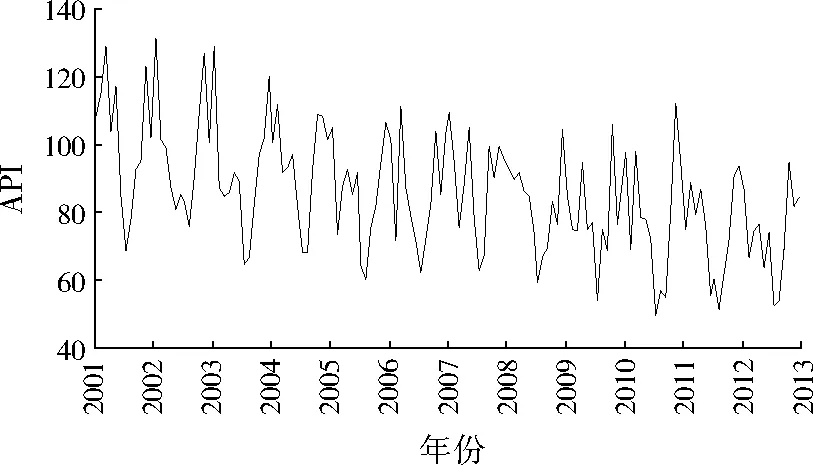
图2 武汉市API月度调整时间序列Fig.2 API adjustment sequence diagram of Wuhan
yt=lnYt
(2)
Zt=(1-B)(1-B12)yt
(3)
式中:yt为Yt的自然对数;Zt为差分后时间序列。
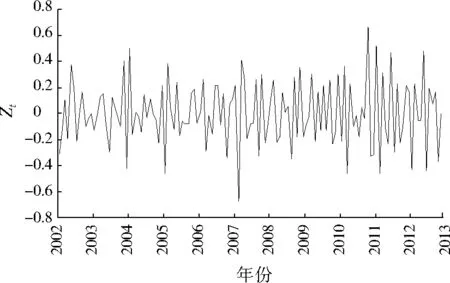
图3 差分后时间序列Fig.3 Sequence diagram of Zt series

延迟/期统计量检验统计量P642.90801287.633018106.5400
由表1可见,差分后时间序列为非白噪声平稳序列(P<0.000 1),达到了ARIMA模型的建立要求,可以进行模型拟合和调整,直至通过白噪声检验,得到API预调整时间序列。由图2可知,武汉市API月度调整时间序列既具有短期相关性又具有季节效应。短期相关性和季节效应无法进行简单、可加性地提取,因此本研究采用ARIMA乘积季节模型进行拟合。根据SBC准则,最终建立的模型为ARIMA(0,1,1)×(0,1,1)12,具体形式为:
(1-B)(1-B12)yt-0.002 276=(1+0.769 529 )(1+0.921 909B12)εt
(4)
运用该模型对武汉市2010—2012年API拟合,其平均绝对误差为8.21%,表明该模型拟合效果较好,可以用来对武汉市API时间序列进行延伸。外推一年的2013年API预测值见表2。
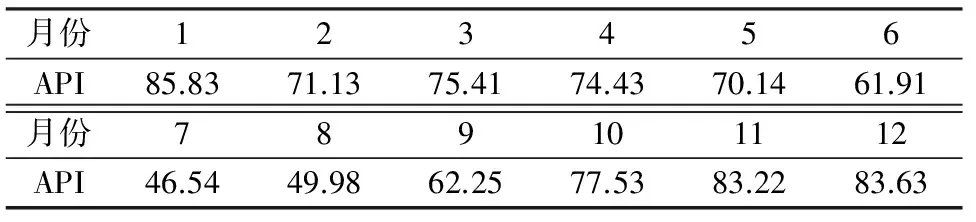
表2 2013年API预测值
2.3 3种成分分析
X-12-ARIMA季节调整方法中季节滤子选择3×5,由于API时间序列具有季节效应和一定的趋势性,本研究选用乘法分解模型。最终将武汉市API时间序列分解为季节、趋势和不规则成分。
2.3.1 季节成分
武汉市API原始和季节调整时间序列如图4所示,其中API_SA为API季节调整时间序列。季节成分影响程度时间序列如图5所示。
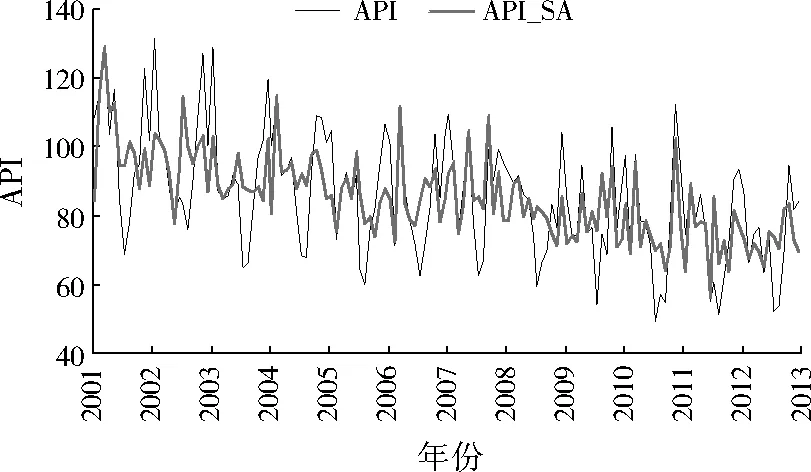
图4 武汉市API原始和季节调整时间序列Fig.4 Wuhan API sequence and seasonally adjusted sequence diagram
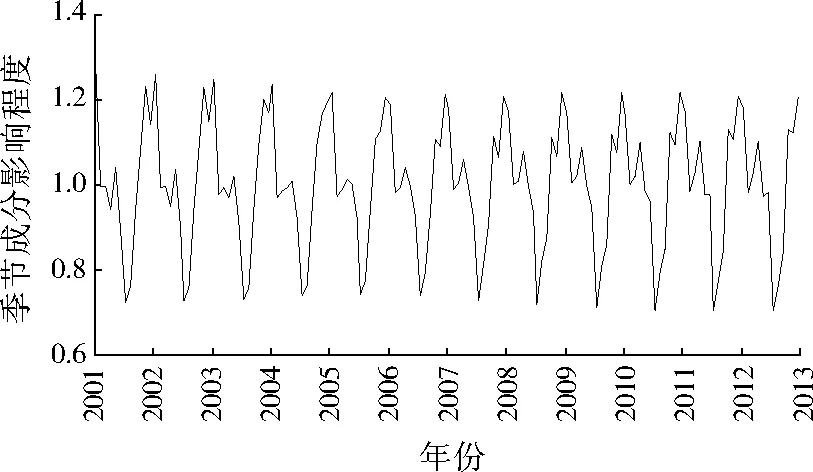
图5 武汉市API季节成分影响程度时间序列Fig.5 Wuhan API seasonal influence degree diagram
图4显示,API_SA较API原始时间序列平滑。整体检验统计量为0.820,此值小于1,表明季节调整效果较好。稳定季节性检验结果(F=21.861,P<0.001)表明,武汉市API存在稳定的季节性。从图5可看出,武汉市API具有明显的季节性特征。变化模式为:每年3月API开始下降,5月略微升高,之后一直到7月开始下降,接着一直上升至11月或12月达到最高,此时季节成分影响程度最高。
2.3.2 趋势成分
如图6所示,武汉市API有整体下降的趋势,武汉市年均API由2001年年均值的101.15降为2012年的72.87,即武汉市环境质量整体往好的方向发展。方差贡献度表明,API变化主要由趋势变化决定,特别是年变化,趋势作用达到85.2%。

图6 API趋势成分时间序列Fig.6 API trend components sequence diagram
2.3.3 不规则成分
结合乘法分解模型在剔除季节和趋势成分后得到API不规则成分时间序列。由图7可见,武汉市API不规则成分影响程度在均值1.02附近波动,并在某些月份(多在冬、春季),不规则成分影响程度大于1,API受不规则成分的影响较大。
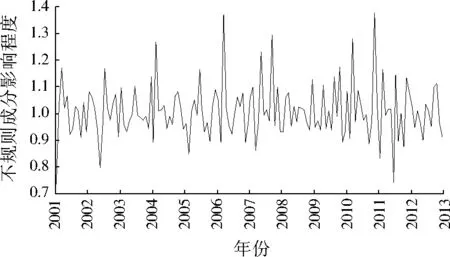
图7 API不规则成分影响程度时间序列Fig.7 API irregular components sequence diagram
2.4 武汉市API变动规律
(1)武汉市API时间序列变动受季节因素影响较大。由图5可知,在夏、秋季受季节成分影响程度小于1,而在冬、春季其影响程度大于1。(2)2001—2012年武汉市API整体呈现下降趋势及一定的周期性。表明武汉市空气质量逐年变好,并呈现出1.5年左右的趋势循环周期(见图6)。(3)API在冬、春季受不规则成分影响较大,且近几年受不规则成分的影响程度增大(见图7)。
3 武汉市空气污染成因分析及改善建议
武汉市空气质量状况整体呈现改善趋势。API下降的原因主要与近年武汉市政府采取的一系列环保措施有关,如关停高污染企业、二环以内燃煤锅炉清洁能源改造和建设两江四岸、全长28 km的江滩生态游园等,并于2010年9月颁布了《武汉市环境保护条例》,加大了环境保护的监管执法力度。此外,武汉市API呈“冬重夏轻”格局,可能与气候因素有关,在污染源不变的情况下,气象条件(风和湍流、温度层结、气压、气温等)是影响大气污染物浓度的主要因素[11]。武汉市属于北亚热带季风性湿润气候,由热带海洋气团和极地大陆气团交替控制。夏季武汉市常受中纬度西风带和副热带高压影响,雨量较其他季节明显增多。据统计,武汉市多年平均降雨量为1 269 mm,且多集中在夏季,并且此时光照强烈,易形成空气对流,空气流动性增强,利于污染物扩散。而冬季常受极地大陆气团控制,气候寒冷干燥,大气层稳定,易形成逆温层,不利于污染物扩散和清除,使得空气污染加重[12]。
根据API的波动特征及研究结论,现提出如下改善空气质量的建议:(1)加强特殊月份环保措施。由图7可知,API在冬、春季受不规则成分影响较大,空气质量较差,因此应在该时间段内加强预防措施,加大治理力度。(2)继续调整产业布局,优化能源结构。从图6可以看出,空气质量逐年变好,说明近年来所采取的一系列环保措施取得了成效。因而,应继续优化能源结构,调整产业布局,推进经济增长方式从粗放型向集约型的转变,加大环境治理力度,达到彻底改善空气质量的目标。(3)扩大绿化面积、加强湖泊保护。扩大市区及周围绿化面积,加强湖泊的保护,能吸附粉尘及其他污染物,调节局地气候,起到城市生态廊道的作用[13],从而达到环境质量改善的效果。
4 结 语
将X-12-ARIMA季节调整方法引入大气分析领域,并以武汉市为研究对象,对其API进行分析,探讨了武汉市API的波动规律并提出了一些环境改善建议。该方法为API分析提供了一个适用的工具,增加了建模技术的可选择性和建模结果的可解释性,有助于定量分析空气污染的变动规律及其深层成因。也可运用该方法对空气污染做进一步分析与研究,并对季节调整方法进行修正使其更适合在环境领域的应用,深入探讨区域性空气污染变动规律,为空气质量的改善提供理论依据。
[1] 段玉森,魏海萍,伏晴艳.中国环保重点城市AQI指数的时空模拟区域分析[J].环境科学学报,2008,28(2):384-391.
[2] 周荣美,应芳,焦荔,等.萧山区环境空气质量变化及其影响因素分析[J].环境污染与防治,2012,34(8):44-48.
[3] 柴微涛,宋述军,宋学鸿.成都市城区空气污染指数的时间序列分析[J].成都理工大学学报(自然科学版),2007,34(4):485-488.
[4] LEE M H A,RAHMAN N H,SULIARTONO M T,et al.Seasonal ARIMA for forecasting air pollution index:a case study[J].American Journal of Applied Sciences,2012,9(4):570-578.
[5] SHISKIN J,YOUNG A H,MUSGRAVE J C.The X-11 variant of the census method Ⅱ seasonal adjustment program[A].Washington,D.C.:Department of Commerce Bureau of Economic Analysis,1967.
[6] BOX E,JENKINS G,REINSEL G.时间序列分析预测与控制[M].王成章,译.4版.北京:机械工业出版社,1997.
[7] FINDLEY D F,MONSELL B C,BELL W R,et al.New capabilities and methods of the X-12-ARIMA seasonal adjustment program[J].Journal of Business and Economic Statistics,1998,16(2):169-177.
[8] 朱发根.基于改进X-12-ARIMA的电煤需求预测模型与实证研究[J].中国电力,2014,47(2).
[9] 王金光.山东省物价波动实证研究——基于季节调整的方法[D].济南:山东大学,2008.
[10] 王燕.应用时间序列分析[M].3版.北京:中国人民大学出版社,2012.
[11] 纪颖,范惠洁,王秋芳,等.颗粒物浓度与气象因素[J].环境与健康杂志,2008,25(6):554-555.
[12] 刘传姚,侯帆,杨玉清,等.武汉市2001—2010年空气污染指数动态分析[J].中国公共卫生,2013,29(6):853-855.
[13] 宗跃光.城市景观生态规划中的廊道效应研究——以北京市区为例[J].生态学报,1999,19(2):145-150.

