有机毒物对小鼠和兔的半数致死剂量与大气环境质量标准的相关性研究*

徐忠香 吴以中 刘顿开

(南京工业大学环境学院，江苏 南京 211800)

随着工业社会的高速发展和城市化进程的加快，环境污染问题日趋复杂，不仅污染物的数量和种类不断增加，而且交互作用形式日益多样化[1]，对人体健康和生态环境造成了极大的危害。因此，控制污染物排放是当前重要任务。

环境影响评价和环境规划领域涉及多种化学污染物，然而目前国内外制定的环境标准并不完整。对于特征污染物的环境质量标准，国内几乎没有相关的研究，国外仅美国环境保护署(EPA)环境实验室推算出化学污染物在各种环境介质(空气、水、土壤)中的含量及排放量的限定值，即多介质环境目标值(MEG)[2-4]。MEG包括周围环境目标值(AMEG)和排放环境目标值(DMEG)[5-6]。环境中污染物对人体或生态系统的影响以及对一些尚没有环境标准值的有毒污染物的评价，可参照MEG。目前共推算了600多种化学污染物的MEG,其中主要是根据大鼠经口给毒的半数致死剂量(LD50)进行估算。

本研究主要通过研究LD50(大鼠)与LD50(小鼠)、LD50(兔)的相关性，拟建LD50(大鼠)与LD50(小鼠)、LD50(大鼠)与LD50(兔)的回归方程，基于MEG理论，推算大气环境目标值(AMEGAH)的估算公式扩展方程，解决环境评价和环境规划领域特征有毒污染物缺少大气环境质量标准的现实问题。根据美国EPA环境实验室推算AMEGAH的估算模式为：

cAH=0.107×crat

(1)

式中：cAH为大气环境目标值，μg/m3；crat为大鼠经口给毒的半数致死剂量，mg/kg。

1 研究方法

由于实验条件有限，现场测定各有机毒物的LD50并不可行，故采用资料收集法。筛选农药、制药等精细化工行业所使用的化学品，收集并整理其毒性数据，使用数学统计法对LD50(大鼠)与LD50(小鼠)、LD50(兔)进行相关性分析。

1.1 数据收集与整理

本次研究需收集大气中各种常见有机毒物对不同物种(大鼠、小鼠以及兔)毒性影响的LD50[7]，由此选取了《工业企业设计卫生标准》(TJ 36—79)、《有毒化学物质毒性手册》、《苏联居民区大气中有害物质的最大允许浓度》中常见有毒物以及美国EPA公布的129种优先控制水环境污染物和中国环境监测总站等单位提出的68种水环境优先控制污染物，共400多种常见化学污染物。通过查询美国国家医学图书馆网站，得到相应的毒性数据。

经过整理，主要验证以下两组数据的相关性：(1)LD50(大鼠)和LD50(小鼠)；(2)LD50(大鼠)和LD50(兔)。

1.2 数学分析方法

本次数据处理使用SPSS 17.0[8]软件，具有数据整理、分析、统计和结果输出等功能。进行统计分析时，相关分析与回归分析是非常重要的手段。相关分析是回归分析的基础和前提，回归分析是相关分析的深入和继续[9]。先利用Pearson线性相关分析研究以上两组数据间是否存在线性相关，若数据间存在相关性，则继续利用线性函数对其进行回归分析；若线性相关度不高，则考虑非线性模型，选择拟合优度高的曲线进行回归分析。若两组数据间不存在线性相关，则证明数据为非正态性分布，进而采用Spearman秩相关分析，若分析结果存在相关性，则继续对数据进行回归分析，建立各组数据间的数量关系即回归方程。

2 数据分析

2.1 LD50(大鼠)与LD50(小鼠)、LD50(兔)的关系分析

2.1.1 线性相关分析

(1) LD50(大鼠)与LD50(小鼠)线性相关分析

图1(选取197组数据)为LD50(大鼠)与LD50(小鼠)相关性分析散点图。由图1可知，两者有相关趋势。经过Pearson线性相关分析，相关系数为0.986，P=0<0.05，即LD50(大鼠)与LD50(小鼠)存在极显著正相关性(见表1)。

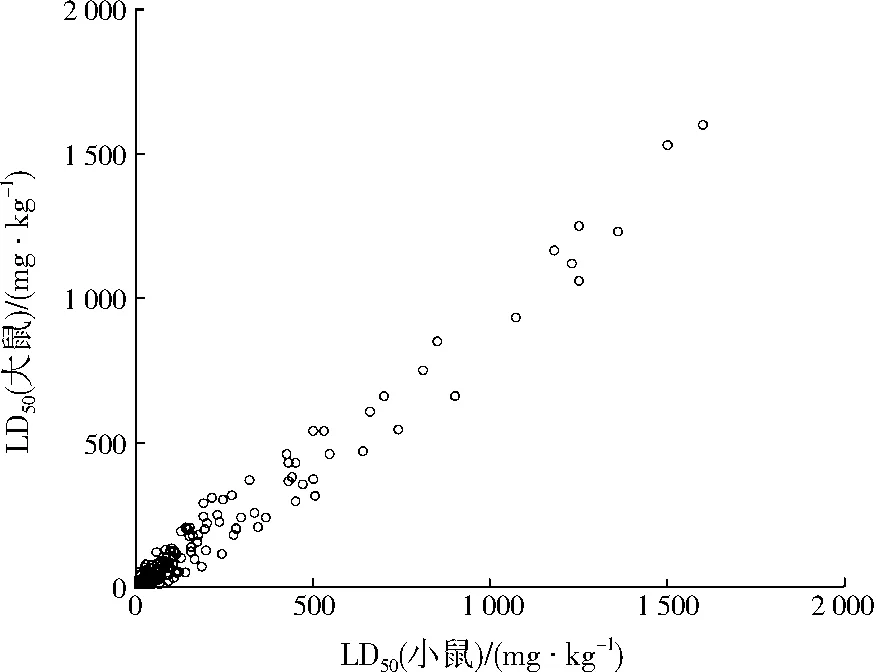
图1 LD50(大鼠)与LD50(小鼠)相关性分析散点图Fig.1 Scatter diagram of correlation analysis between LD50 (rat) and LD50 (mouse)

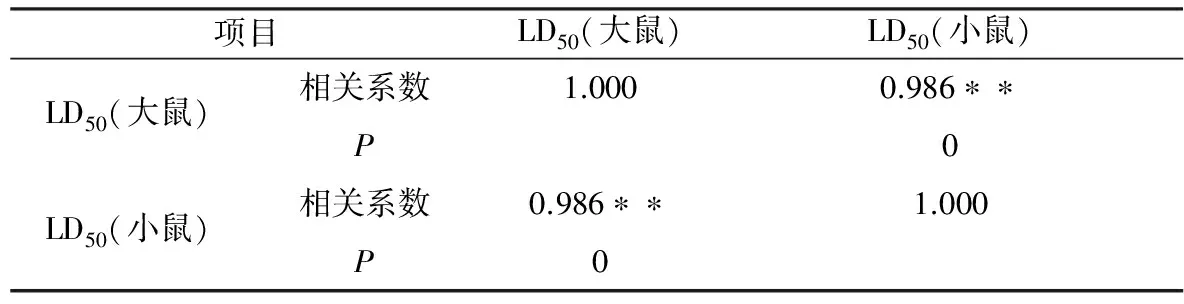
项目LD50(大鼠)LD50(小鼠)LD50(大鼠)相关系数1．0000．986∗∗P0LD50(小鼠)相关系数0．986∗∗1．000P0

注：1)**表示在0.01水平(双侧)上极显著相关，表2同。(2) LD50(大鼠)与LD50(兔)线性相关分析

图2(选取110组数据)为LD50(大鼠)与LD50(兔)相关性分析散点图。从图2可以看出，两者有相关趋势。同理，经过Pearson线性相关分析，相关系数为0.980，P=0<0.05，即LD50(大鼠)与LD50(兔)存在极显著正相关性(见表2)。

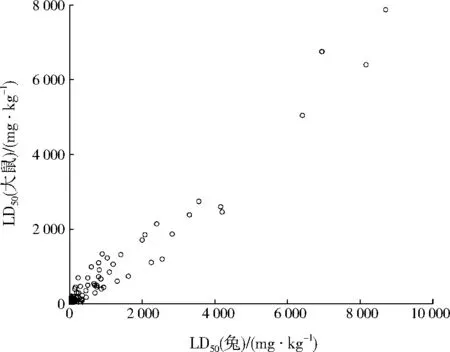
图2 LD50(大鼠)与LD50(兔)相关性分析散点图Fig.2 Scatter diagram of correlation analysis between LD50 (rat) and LD50 (rabbit)

项目LD50(大鼠)LD50(兔)LD50(大鼠)相关系数1．0000．980∗∗P0LD50(兔)相关系数0．980∗∗1．000P0

2.1.2 线性回归分析

经过初步线性相关分析，上述两组数据均呈正相关性，可进一步进行回归分析，拟建回归模型。

(1) LD50(大鼠)与LD50(小鼠)的线性回归分析

由表3可知，LD50(大鼠)为因变量，LD50(小鼠)为自变量，回归模型的判定系数(R2)为0.972，说明自变量可解释因变量97.2%的变异量，对模型自身的检验P=0<0.05，说明LD50(小鼠)对于LD50(大鼠)的回归方程是成立的。由于常数项检验P=0.727>0.05，接受常数项为0的假设，方程的常数项为0；LD50(小鼠)的b1检验P=0<0.05，拒绝为0的假设，方程b1为0.992(见表4)。

回归分析的结果显示，LD50(小鼠)对LD50(大鼠)有预测作用，拟合的回归方程如下：

crat=0.922cmouse

(2)

式中：cmouse为小鼠的半数致死剂量，mg/kg。

(2) LD50(大鼠)与LD50(兔)的线性回归分析

由表5可知，LD50(大鼠)为因变量，LD50(兔)为自变量，回归模型的R2为0.960，说明自变量可解释

因变量96.0%的变异量，对模型自身的检验P=0<0.05，说明LD50(兔)对于LD50(大鼠)的回归方程是成立的。由于常数项检验P=0.729>0.05，接受常数项为0的假设，方程的常数项为0；LD50(兔)的b1检验P=0<0.05，拒绝为0的假设，方程b1为0.831(见表6)。

回归分析的结果显示，LD50(兔)对LD50(大鼠)有预测作用，拟合的回归方程如下：

crat=0.831crabbit

(3)

式中：crabbit为兔的半数致死剂量，mg/kg。

通过上述分析结果可知，LD50(大鼠)与LD50(小鼠)、LD50(兔)均存在相关性，并得到线性回归方程。但是否存在拟合效果更佳的回归方程，有待后续分析。故继续对两组数据进行非线性回归分析。

2.1.3 非线性回归分析

选取常见的10种曲线模型，采用曲线估计，选择拟合优度较高的曲线进行回归分析。

(1) LD50(大鼠)与LD50(小鼠)的非线性回归分析

表3 LD50(大鼠)与LD50(小鼠)线性回归模型分析

注：1)表示方程的回归系数，表4至表7、表9同。

表4 LD50(大鼠)与LD50(小鼠)线性回归系数分析

表5 LD50(大鼠)与LD50(兔)线性回归模型分析

表6 LD50(大鼠)与LD50(兔)线性回归系数分析

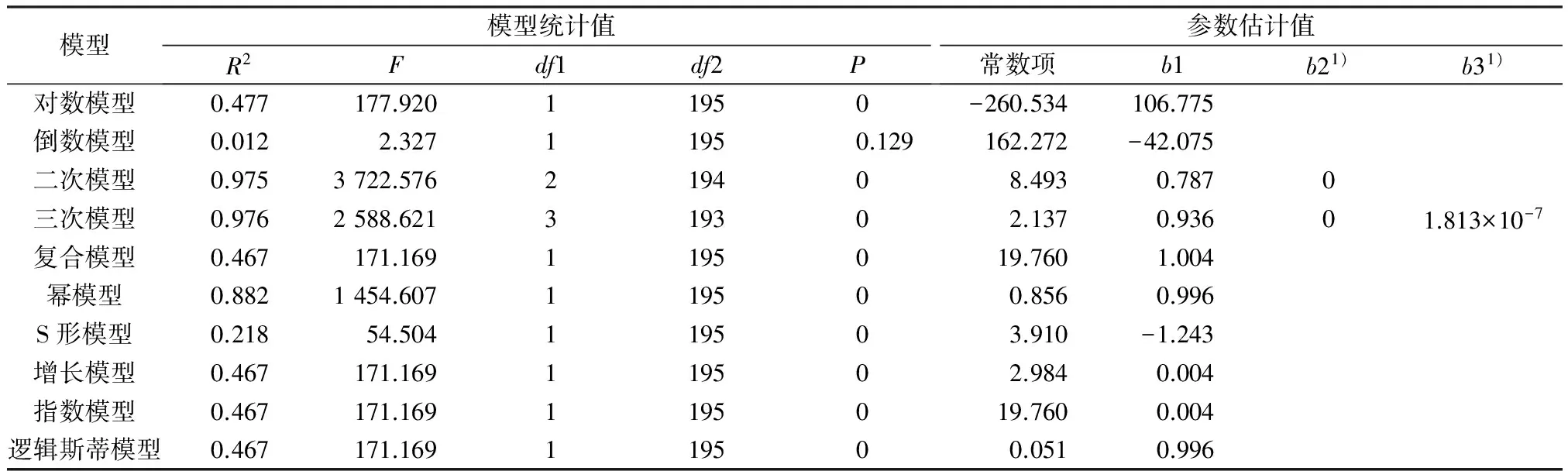
表7 LD50(大鼠)与LD50(小鼠)非线性回归模型汇总

注：1)表示方程的回归系数，表9同。

表8 LD50(大鼠)与LD50(小鼠)三次模型系数分析

从表7可以看出，10种曲线模型中三次模型拟合优度最高(R2=0.976)，方差检验的F统计量为2 588.621，P=0<0.05，说明回归方程整体达到显著水平，LD50(小鼠)对LD50(大鼠)的非线性回归方程是成立的。其三次模型曲线见图3。由表8可知，三次模型的常数项检验P=0.644>0.05，所以接受常数项为0。由参数估计值可得到回归方程：

(4)

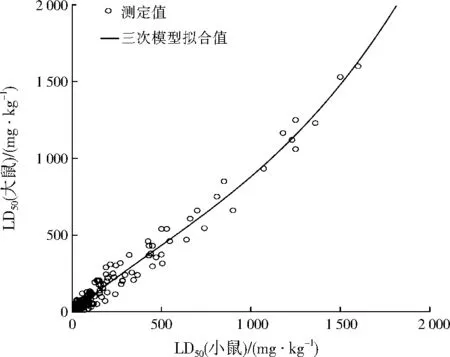
图3 LD50(大鼠)与LD50(小鼠)的三次模型曲线Fig.3 Cubic function curve of LD50 (rat) and LD50 (mouse)

(2) LD50(大鼠)与LD50(兔)的非线性回归分析 从表9可以看出，二次、三次模型拟合优度相同且最高(R2=0.968)，选择系数较少的二次模型。方差检验的统计量F为1 618.831，P=0<0.05，说明回归方程整体达到显著水平，LD50(兔)对LD50(大鼠)的非线性回归方程是成立的。其二次模型曲线见图4。由表10可知，二次模型常数项检验P=0.056>0.05，接受常数项为0的假设。根据参数估计值可得到回归方程：

(5)

2.2 分析结果

通过以上分析，可得到结论如下：

(1) LD50(大鼠)与LD50(小鼠)具有极显著正相关性。

(2) LD50(大鼠)与LD50(兔)具有极显著正相关性。

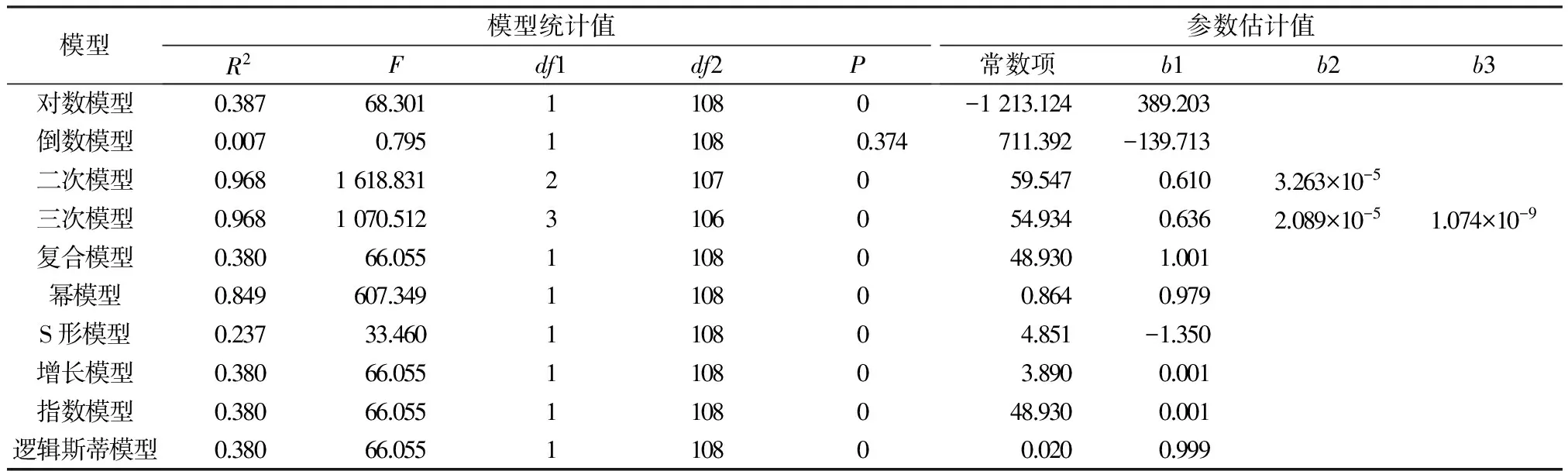
表9 LD50(大鼠)与LD50(兔)非线性回归模型汇总

表10 LD50(大鼠)与LD50(兔)二次模型系数分析

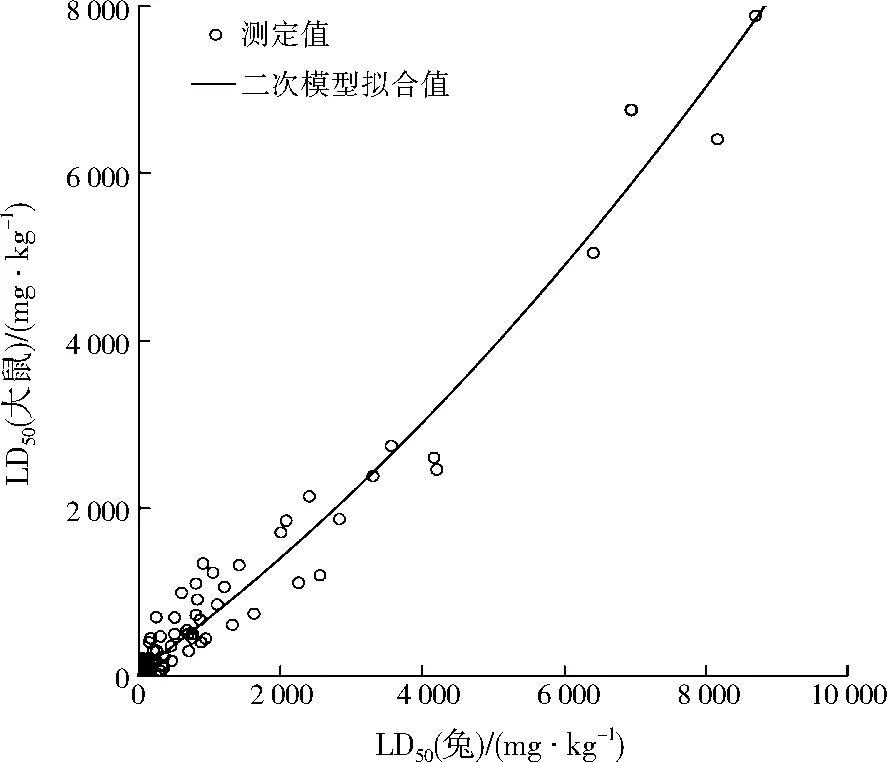
图4 LD50(大鼠)与LD50(兔)的二次模型曲线Fig.4 Quadratic function curve of LD50 (rat) and LD50 (rabbit)

在线性和非线性回归分析中，发现线性回归方程的R2比非线性回归方程小，即非线性方程拟合优度高，相比之下，所得到的非线性回归方程更能解释两组数据的相关关系。因此，选用非线性回归方程。

2.3 AMEGAH的扩展方程

由于计算AMEGAH以代入大鼠经口给毒LD50为佳，所以利用以上得到的两组回归方程能在未知大鼠经口给毒LD50的情况下，已知其他两个数据中任意一个，计算大鼠经口给毒LD50。

将式(4)、式(5)代入AMEGAH的估算式(1)中，得到AMEGAH与LD50(小鼠)、LD50(兔)的关系式，如下：

(6)

(7)

3 结 语

研究表明，LD50(大鼠)与LD50(小鼠)、LD50(兔)存在极显著正相关性，在MEG理论基础上，由LD50(大鼠)与LD50(小鼠)、LD50(大鼠)与LD50(兔)的回归方程建立了利用LD50(小鼠)和LD50(兔)推算的AMEGAH扩展方程，可在已知LD50(大鼠)、LD50(小鼠)、LD50(兔)其中任意一个数据的情况下，计算AMEGAH作为有机毒物大气环境质量标准的推荐值，从而解决了数据库中毒性数据不完整而无法推算有机毒物大气环境质量标准的难题。短期内，国家环境标准不可能包括现有特征有机毒物，因此AMEGAH扩展方程的建立，有效地解决了有机毒物环境标准限值缺乏的问题，可用于特征污染物环境评价和环境规划等环保工作。

[1] 周启星.复合污染生态学[M].北京：中国环境科学出版社，1995.

[2] HJ 611—2011，环境影响评价技术导则 制药建设项目[S].

[3] HJ 582—2010，环境影响评价技术导则 农药建设项目[S].

[4] 汪晶，和德科，汪尧衡.环境评价数据手册——有毒物质鉴定值[M].北京：化学工业出版社，1988.

[5] 吕平毓，米武娟.多介质环境目标值在环境评价中的应用[J].人民长江，2012，43(1)：59-62.

[6] 暨仕臣，李芬芳，侯文斌，等.多介质环境目标值的应用[J].重庆环境科学，1992，14(6)：31-34.

[7] 孟紫强.环境毒理学[M].北京：中国环境科学出版社，2000.

[8] STERN L D.A visual approach to SPSS for wndows:a guide to SPSS 17.0[M].Boston:Allyn & Bacon,Inc.,2009.

[9] 王瑞卿.统计学基础[M].北京：北京大学出版社，2009.