基于CMOS相机的轨道车辆动态包络线测试
关 岳
(中车青岛四方机车车辆股份有限公司工程实验室,山东 青岛266111)
0 引言
铁路最初是以结构限界来校验机车车辆轮廓的,然后发展到考虑车体和线路的误差、静态变形和磨耗的静态限界。在此基础上,进一步考虑悬挂的静态、准静态和动态振动变形,得到车辆的动态限界(亦称“动态包络线”)。
车辆动态包络线定义为车辆运行过程中受各种不利因素影响所导致的最大极限轮廓。在基准坐标系内,以计算车辆轮廓线上各坐标点为基准点,涉及了车辆和轨道的公差、磨耗、弹性变形、车辆各种振动及滚动等原因,将车辆在运行中偏离基准点的最大位置作为车辆动态包络线。
车辆动态包络线目前主要依靠理论计算、线路实测和实验室试验进行获取。理论计算计算方法有多种,得到的结果往往不一致,也偏于保守,还需要试验验证。计算的方法求取动态包络线,计算过程中所涉及的参数多为主观取值,且无法将随机因素考虑在内,计算结果不能真正客观地反映实际情况。线路实测限制于测量位置,单次试验只能体现一个工况,不能代表所有的工况,需要多次试验才能获取完整的试验数据。动态位移的静态测量虽然能通过试验获取位移数据,比纯理论计算更具有现实性,但毕竟仅是静态的试验,与动态试验还是有巨大区别。
为此,开展基于整车振动模拟试验台的车辆动态限界试验方法研究。振动台根据路试采集的路谱对整车车身进行振动试验,模拟车辆在道路运行中的振动,使车身产生动态变形,变形量由动态位移测量系统测出,进而得到动态包络线。整车振动试验流程如图1所示。

图1 整车振动试验流程图
其中动态位移测量系统通过识别位于机车车身截面上的目标位置在试验过程中的变化,获得车辆的横向运动轨迹,利用软件进行计算得到各个观测目标在车辆坐标系中随时间的位置变化规律。
1 测量原理
试验中需要测量的是控制点在机车车身坐标系中垂直于车身方向的变化量。利用单目视觉测量原理,采用大面积、高分辨率、快速传输图像的CMOS数字相机,配合低畸变大光圈光学镜头,获取固定在机车车身截面的主动光学目标位置的变化,经高性能图像处理器处理,实现被测点图像的快速采集,集中处理、分析,利用坐标分析管理软件给出被测点的在实验过程中的变化情况,最终实现车辆动态限界的非接触测量,给出动态限界的测量结果,变化量和动态限界。系统示意图如图2所示。
动态位移测量系统主要包括:图像获取系统、主动发光目标、相机标定系统、标尺、计算机硬件系统、图像处理软件、坐标分析管理软件等。
1.1 成像模型
本系统以相机的透视投影模型为基本理论基础,利用POSIT算法求解出光学靶标所在空间坐标系相对于摄像机坐标系的旋转矩阵R及平移矩阵T,进而得到光学靶标的位置量和姿态量。
有关相机透视投影模型国内外已经有大量文献可供参考,本文不再做具体推导,对算法所涉及的公式直接引用。为便于描述,对常用坐标系进行了如下定义(见图3),设OcXcYcZc为相机坐标系,Oixy为像平面坐标系,Oiuv为计算机图像坐标系,OcOi的距离为相机成像镜头的有效焦距f。

图3 针孔相机模型
待求的位姿数据中包括物体坐标系相对于相机坐标系的旋转矩阵R和平移向量T。其中:
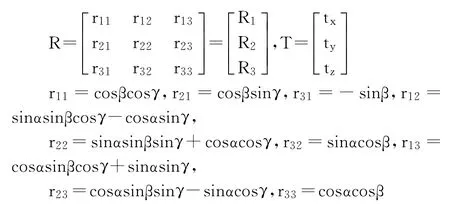
相机的坐标系通过测量车身上已知坐标的参考点统一到车身坐标系中。
1.2 位姿解算
POSIT(Pose from Orthography and Scaling with Iteration)是1992年首次提出的用于计算三维物体姿态的一种算法。其中的位置信息T和姿态信息R由6个参数描述。
算法分两部分:(1)带有比例系数的正交投影变换(Scale Orthogonal Projection,SOP),根据线性方程组求出旋转矩阵和平移向量;(2)由得出的旋转矩阵和平移向量系数,更新比例系数(scale factor),再由比例系数更新原有的点,进行迭代。
1.3 角度计算
采用式(1)可从旋转矩阵R即可求解出物体坐标系分别绕x轴、y轴和z轴各自的旋转角度α、β和γ。
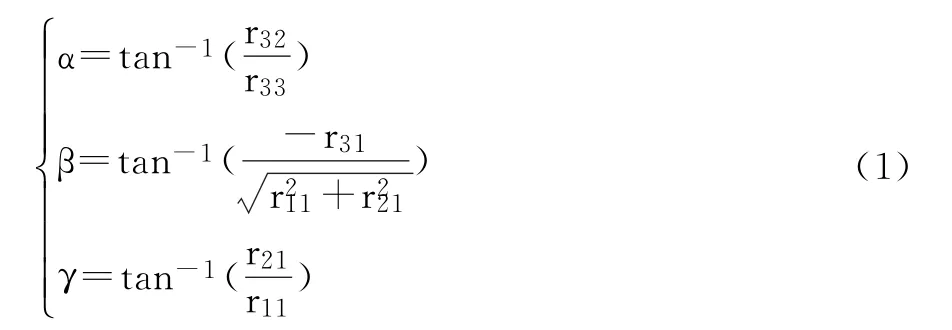
物体在空间的相对位置变动T'=(ΔX,ΔY,ΔZ)T T′=[Δx,Δy,Δz]T 是物体坐标系 OWXWYWZW原点移到相机坐标系OcXcYcZc的相对变化量,因此可由前面所求的平移矩阵T的反向向量得到,即:
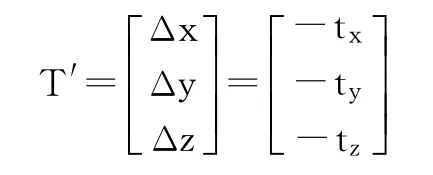
1.4 目标点特性
为了增强目标的可识别性,使用主动光学目标。主动光学目标固定在车身端面,试验中随车身一起振动。目标点采用Ir LED,发射角约120°,根据使用需要,采用不同措施可将Ir LED的光斑调节为不同类型。
常用的Ir LED光斑为均匀光斑或高斯光斑。如图4所示。对其中高斯光斑的一个截面用Matlab的曲线拟合工具进行拟合,得到的拟合参数R-square为0.9908,说明所用的Ir LED光斑可以当作高斯光斑分析和处理。
1.5 光斑位置计算
光斑“中心”的计算方法,取决于光斑的类型。对于均匀光斑,一般可采用边缘检测获取光斑边缘,再进行圆或椭圆的方法定位中心,通常能达到像素级的定位精度。而对于高斯光斑,可以采用的定位算法较多。其中以高斯拟合的方法为最优,能取得0.1像素以内的误差。
二维高斯曲面的解析方程为
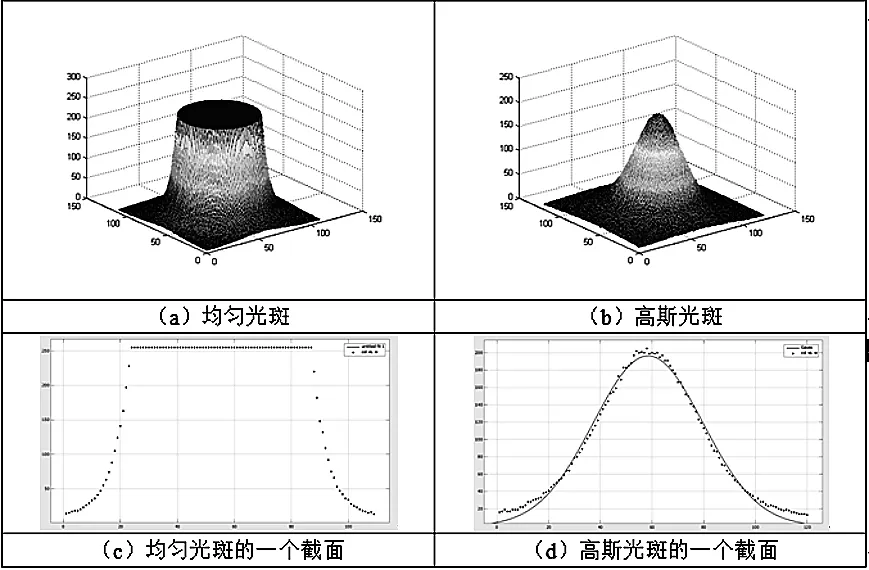
图4 均匀光斑和高斯光斑
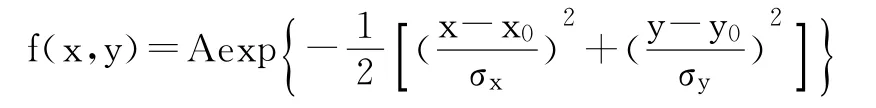
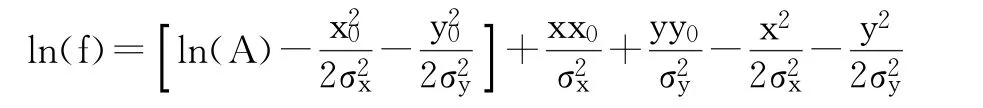
两边都乘以fi(xi,yi)引入灰度信息后简化为

根据最小二乘法,在残差的平方和最小的约束下,求得
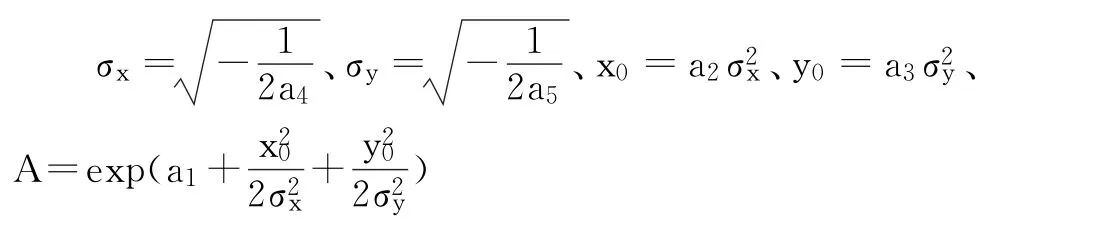
2 相机选择
2.1 被对象主要参数
被测的机车车身端面尺寸约为6m×4m,最大振动频率10 Hz,最大振幅300mm。
2.2 相机
为了满足测量需要,相机选择时首先考虑大相面、高分辨率以满足测量范围和分辨率的要求,其次考虑帧率要满足测量速度的要求。经过比较选择分辨率为5,120×3,840,像素尺寸6.4μm,最高帧率为30的CMOS数字相机。对应测量范围为6m×4m时,像素的物理分辨率能达到1.17mm×1.04mm,使用高斯拟合的亚像素的提取算法能达到0.1像素以内,则系统的分辨率约为0.12mm。
2.3 相机的光谱响应
相机对不同波长的响应效率是不同的。如图中上面一条曲线所示,波长约600nm时相机的响应效率最高约为65%。为了目标的便于识别,采用中心波长为730nm的Ir LED,效率约为50%,可满足使用的需要。
3 相机性能测试
3.1 相机快门时间的影响
相机的快门时间影响成像的光斑。图6给出了同样的运动速度下,不同快门时间同一个主动目标所成的光斑图像。

图5 相机的量子效率

图6 不同快门时间图像的比较
由图6可见,光斑的类型和成像的形状都不同。随着快门时间的增大,同样亮度的主动目标所成图像的亮度在增加,直至饱和。较长的快门时间使得主动目标在快门开启时经过更长的距离,使得光斑的形状更不“圆”。在此过程,光斑由接近高斯分布变得更接近均匀光斑。
3.2 被测物体速度的影响
被测的对象处于动态震动的状态,要求相机可较快的速度成像。为此,将主动目标点安装到圆轨迹发生器,模拟试验中的动态目标,对相机的测量能力进行试验。如图7所示,目标可以按照设定的速度沿圆周运动。在4种速度条件下,测试相机的成像能力和测量误差。对0.5m/s和1.0m/s速度下,7个快门速度分别进行了测试,对1.5m/s和2.0m/s的速度下,选取部分快门进行了测试,测试结果见表1。

图7 相机的量子效率
表中的测量误差为实际测得的主动目标的圆形轨迹的半径与参考值之差。
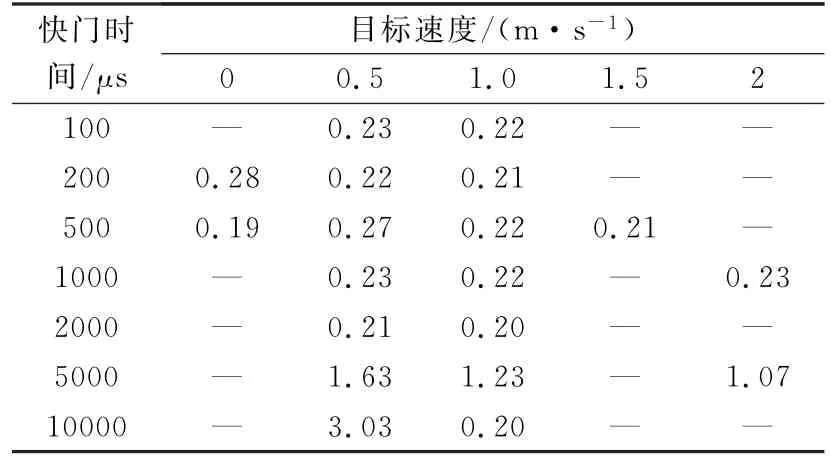
表1 不同速度下的测量误差
表1中给出各速度和快门时间下,所测得的圆形轨迹与理论值之差。从数据可以看出,在保证成像光斑的质量条件下,同样的速度下,较短的快门时间的误差更小;同样的快门时间条件下,更快速度下的误差更小。这从两方面说明了被测物体的速度决定了所使用的快门的时间;若条件允许,使用较短的快门时间。
4 图像采集软件
系统以单目视觉测量原理为理论基础,测量过程中有大量的数字图像处理的计算过程,由于所使用的是2000万相机的高分辨率相机,造成单幅图像的体积较大,约18.75MB。考虑到最高的帧率为30fps,则每秒的数量量约562.5MB,每分钟的数量量约33GB。这么大的数据量对数据的存储容量和存储速度、数字图像处理速度都提出了较高的要求。
图像处理的方式采用CPU+GPU并行处理方式,CPU负责运算的逻辑部分,GPU完成数字图像的并行计算。拟使用的GPU平台为支持 CUDA 3.0技 术 的NVIDIA Quadro M4000的加速卡。
图像处理的流程见图8。
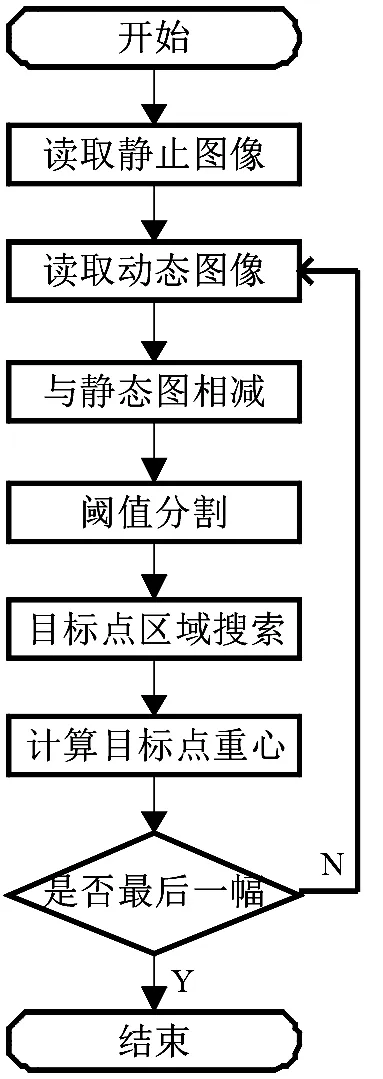
图8 数字图像的处理流程
5 结论
本文给出了基于大面积CMOS数字相机的动态限界测试系统,详述了测量的原理、主动目标的定位算法和相机的选用,根据测量的需要,对相机的性能进行了测试。测试结果表明相机可以满足使用要求。
[1]景建辉,吕凤梅,邵楠,等.CRH3型动车组动态限界设计技术研究[J].大连交通大学学报,2014,35(2);20-24,35.
[2]滕万秀,程亚军.车辆限界计算方法对比研究[J].都市快轨交通,2009,22(4):40-45.
[3]罗仁,滕万秀,干峰.铁道车辆动态包络线计算方法研究[J].铁道车辆,2014,52(3):1-5.
[4]郭寅.高速列车动态包络线测量系统[J].中国激光,2013,40(2):1-7
[5]陆冠东.车辆限界校核中动态位移的静态测量[J].铁道车辆,2008,46(2):1-4.
[6]Gary Bradski,Adrian Kaebler.学习OpenCV(中文版)(第一版)[M].北京:清华大学出版社,2009.
[7]马颂德,张正友.计算机视觉:计算理论和算法基础[M].北京:科学出版社,1998.
[8]张广军.机器视觉[M].北京:科学出版社2004:84.
[9]马骊群,曹铁泽,王继虎等.大尺寸坐标测量技术在大型部件装配应用中的若干问题[J].计测技术,2013,33(2):7-11.
[10]甘晓川,赫明钊,叶孝佑.数字近景摄影测量中相机内参数校准[J].计量学报,2012,33(5):391-394.
[11]Zhang Z.Y.,A Flexible New Technique for Camera Calibration[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2000,22(11):1330-1334.
[12]甘晓川,孙安斌,叶欣等.一种非接触单相机角度测量方法[J].计量技术,2014,(11):7-11.
[13]李帅,卢荣胜,史艳琼等.基于高斯曲面拟合的亚像素边缘检测算法[J].工具技术,2011,45(7):79-82.

