高房价下山东省制造业集聚的空间效应分析——基于空间面板模型的实证

文/崔凌云



高房价下山东省制造业集聚的空间效应分析——基于空间面板模型的实证

文/崔凌云

摘要：本文选取2009-2013年山东省17地市两位数制造业统计数据，分析了山东省制造业集聚的特征并采用空间杜宾面板模型测算了资本投入、劳动投入、制造业集聚以及房价上涨对制造业产出的空间效应。本文的实证过程中采用了三种不同的权重矩阵，结果显示，当前山东制造业生产过程中，资本投入的直接效应较小，溢出效应较大；无论采用何种权重衡量，劳动投入的产出弹性均远大于资本投入，且制造业中劳动力为稀缺要素。

关键词：产业集聚；平均集中率；空间杜宾面板模型；空间溢出效应

经济活动在空间上各地理单元间的分布往往不均衡，特别是在工业生产中。若特定产业的很大份额集中在少数几个地区，其空间分布越不均衡，产业集聚程度越高。美国经济学家波特认为这种产业集聚具有外部经济，通过规模收益递增和创新可以促进产业发展和地区经济增长。近年来，各级政府越来越认可产业集聚的正外部性，通过推动邻近地区经济一体化来促进有序的产业集聚，实现1+1>2的效果。跨省的区域经济一体化主要有珠江三角洲一体化、长江三角洲一体化和京津冀一体化，各省省内也有局部一体化战略，如山东省2013年确立了“两区一圈一带”发展战略，划分了山东半岛蓝色经济区、黄河三角洲高效生态经济区、省会城市群经济圈和西部经济隆起带①。

学界也认可产业集聚的作用。新经济地理的中心-外围论从动态角度刻画了有序产业集聚的三阶段：第一阶段，企业和工人向一个地区集中，地区专业化生产水平提高，初步形成“中心-外围”结构；第二阶段，为避免过度拥挤，资源密集型产业有序向外围转移；第三阶段，实现区域内自由贸易和专业化分工，本区域工业生产水平显著上升。随着政府主导的区域一体化向纵深发展，空间视角下的产业集聚成为近几年学术讨论的热点。范剑勇、李方文（2011）发现地市级层面制造业分布较为平均，城市体系的扁平化特征明显，但县级层面的产业集聚趋势非常明显；宋马林等（2012）利用我国中部六省88个地市8年数据，采用LISA统计分析了第二产业的空间集聚与扩散状态，通过马尔科夫链模拟，找到了各状态之间的转移概率，预测了其未来发展状态；徐文娟、钟立新（2015）比较了广东、浙江两省5年间两位数制造业的产业集聚情况，其指标包括静态与动态SP指数、MoranI指数和制造业中心值，说明两省间产业集聚与扩散的行业存在差异。以上文章仅分析了产业集聚的空间相关性，并未利用空间面板分析其影响因素。在既有基础上，本文将使用空间面板模型研究山东省17地市制造业集聚对工业生产的空间影响。

一、指标说明

本文选择以地区制造业平均集中率衡量产业集聚水平，其计算公式为：

其中，i代表地市，N为地市数量，r代表细分行业，R为细分行业部门的数量，为i地市r细分行业的工业总产值，为i地市r细分行业的工业总产值占全省该细分行业工业总产值的份额。即为i地市的制造业平均集中率，该指标越大，表明制造业在特定地区越集中。

本文选取山东省2009-2013年17地市28个制造业细分行业②的工业总产值，代入公式计算各地市及经济区 的制造业平均集中率。2013年制造业集聚程度较高的城市是青岛、烟台和威海，较低的城市是莱芜、日照和济宁，前者2013年制造业总产值排名第1、2和10位，且都位于山东半岛，后者的总产值排名17、16和13，且多位于鲁西南地区，说明发达的制造业和其集聚程度呈正相关。与2009年相比，2013年山东省17地市中，集聚程度上升的有9个，其中居前三位的是泰安（0.028）、东营（0.027）和德州（0.017）；集聚程度下降的有8个，居前三位的分别是潍坊（-0.031）、烟台（-0.03）和济南（-0.02）。

二、计量方法

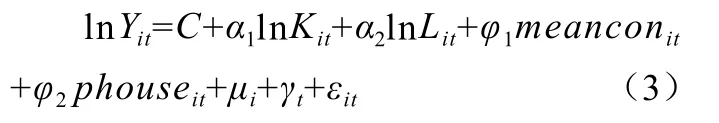
（一）空间计量方法

静态空间面板模型可以表示为：

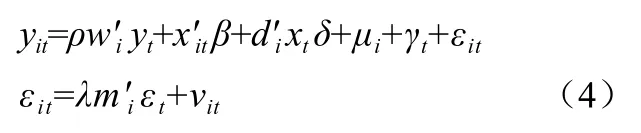
式（4）中ρ、β和δ均为未知系数，根据Elhorst2012年设计的方法，可以通过假设检验检验SDM是否可简化为SAR，通过假设检验检验SDM是否可简化为SEM。因此，本文空间面板模型为：

（二）变量选取

本文采用山东省17地市的主要经济指标为样本，样本区间为2009-2013年，数据来源为各地市各年的统计年鉴，变量选取和数据描述如下：因变量：lnY，其中Y为各地市各年的两位数制造业（细分行业）工业总产值,以2009年为基期，用地区生产总值指数对其进平减处理。本文将实际工业总产值取对数得到lnY，反映制造业的发展水平。主要解释变量：lnK，其中K为各地市各年制造业固定资产净值③，以2009年为基期，用地区生产总值指数进行了平减。本文将实际固定资产净值取对数得到lnK。资本投入主要是固定资产投入，它是制造业生产的基础；lnL，其中L为各地市各年制造业从业人员数，取对数后得到lnL，劳动投入同样是制造业生产不可或缺的条件；meancon，为各地市各年的制造业平均集中率，衡量产业集聚程度，计算方法见前文第二部分的指标说明。控制变量：phouse为房价上涨率，在各地市各年的统计年鉴中，有上年为100的新建住宅销售价格指数④，该指数减去100即为phouse。

（三）空间权重矩阵的构建

本文构建三种空间权重矩阵来进行空间计量分析。

一是高速公路里程数权重矩阵W1。根据地理学第一定律,任何事物与周围事物之间均存在联系，而距离近的事物比距离远的事物联系密切，因此在描述本文样本的空间结构时，首先考虑距离权重矩阵W1。令不同地市i和j间高速公路的里程数为d，则

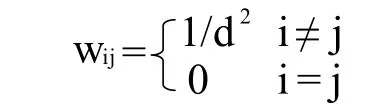
为W1中对应元素，并在矩阵内按行进行标准化。

二是邻接权重矩阵W2。不同地市i 和j若相邻则为1，不相邻在为0，这表现为在矩阵W2中，对角线上元素为0，其它元素为

同样，矩阵W2中按行进行标准化。

三是经济活动权重矩阵W3。制造业生产或集聚本身是经济活动，单纯以地理距离或邻接来刻画其空间结构不够细致，还要综合考虑非地理因素的影响。因此，在借鉴了李靖等（2010）的思路后，本文的W3为：其中，Y为各地市各年制造业实际工业总产值，为考察期内第i地市制造业实际总产值平均值，为考察期内制造业实际总产值的平均值。

三、模型选择和结果分析

（一）模型选择

为选择出适合本文样本的空间面板模型，根据Elhorst2012年设计的方法，第一步估计无空间效应的面板模型并进行LM检验：

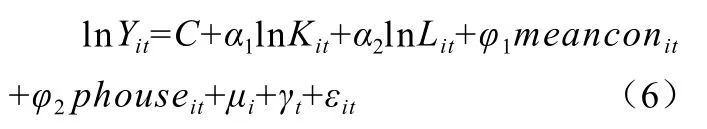
本文数据N（17）大T（5）小，因此属于短面板模型固定效应模型更适合。运行Elhorst提供的Matlab程序包可以看出⑤，空间固定效应中应考虑残差项的空间自相关，空间时间双固定效应中是否应包含因变量的空间滞后项和残差项的空间自相关，需要进一步检验。

为确定空间固定效应和时间固定效应的联合显著性，需进行LR检验。LR检验结果显示⑥，空间固定效应和时间固定效应均呈现1％水平上的联合显著，因此应建立空间时间双向固定效应模型。

根据Elhorst2012年设计的方法，第二步进行Wald检验和LR检验，判断面板模型是否可简化为SAR面板模型或SEM面板模型。检验的判断标准为，对于两项原假设和如果不能拒绝且第一步中LM检验和稳健LM检验显示因变量的空间效应显著，则应选用SAR面板模型；如果不能拒绝且第一步中LM检验和稳健LM检验显示残差项的空间效应显著，则应选择SEM面板模型；如果两项原假设均可拒绝，则应选择SDM面板模型。

根据联合显著性检验结果，本文对空间时间双固定效应模型进行Wald检验和LR检验，结果见表1。表1中第一列为基于极大似然法（QML）估计的空间杜宾模型，第二列为基于Yu和Lee （2008）的纠偏QML估计。这里T=5， N=17,满足N>T，T>N1/3=2.57，根据Yu 和Lee（2008）的研究，此时应使用纠偏QML。第一列的Wald检验和LR检验均在5％显著水平拒绝了两项原假设和第二列在10％显著水平亦可拒绝两项原假设和即此时空间杜宾模型（SDM）不能简化为SAR或SEM，第三列的估计结果检验在5％显著水平也支持空间杜宾模型（SDM）。对于应选择第三列的空间随机时间固定效应模型的估计结果，还是第二列的空间时间双固定效应模型的估计结果，Hausman检验的统计量为10.32，其p值为0.3248，故不能拒绝空间随机效应的原假设，此时应选择第三列的估计结果。

（二）结果分析

根据表1中第三列的估计结果，本地资本投入的产出弹性为0.083，劳动投入的产出弹性为0.305，这两项系数均在5％水平显著。其他地市资本投入亦能增加本地制造业产出，其系数为0.472，在1％水平显著，这表明资本在山东并不稀缺，制造业资本的使用不存在竞争性，且各地市间制造业产出是相互促进的；值得注意的是，现阶段其他地市资本投入对本地产出的增加系数0.472远大于本地资本和劳动的产出增加系数0.083和0.305，这表明制造业应协调各地市后统一发展。本地制造业集聚程度对产出的影响为11.065，在1％水平显著，其他地市制造业集聚对本地产出的影响为-3.561，在10％水平不显著，说明产业集聚仅在本单元内规模收益递增和知识溢出，这种经济外部性还不能在相邻空间单元显著扩散。估计结果还显示出，本地房价上涨将减少本地制造业产出，其他地市房价上涨将增加本地制造业产出，但两项系数（绝对值）均非常小，且不显著。

表1中的结果由高速公路里程数权重矩阵W1获得，为比较产业集聚的相互影响，表2中利用邻接权重矩阵W2和经济活动权重矩阵W3对本文样本再次进行估计，其结果依然支持空间随机和时间固定的SDM模型。

当考虑邻接关系时，模型（2）给出，本地资本投入的产出弹性为0.077，在10％水平显著，本地劳动投入的产出弹性为0.388，在1％水平显著，产业集聚对本地产出的影响系数为10.086，在1％水平显著，本地房价上涨将使本地产出减少，但其系数如模型（1）一样，非常小且不显著。邻接地市资本投入对本地制造业产出的弹性为0.171，在5％水平显著，此项系数远小于以W1为权重矩阵时的系数0.472，说明资本溢出效应主要发生在非邻接地市。邻接地市的产业集聚水平和房价涨幅对本地制造业生产影响与以W1为权重矩阵时基本相同，且都不显著。（见表2）

表1　包含空间时间双固定效应的空间杜宾模型（SDM）估计

当综合考虑经济活动的影响时，模型（3）给出，本地资本投入的产出弹性降为0.066，在10％水平显著，本地劳动投入的产出弹性将为0.285，在5％水平显著，本地产业集聚水平的影响系数为10.245，比模型（2）中略有下降，同样也在1％水平显著。本地房价上涨对本地制造业产出的影响为负，但同前两个模型一样，系数非常小且不显著。在以经济活动权重矩阵W3衡量的模型（3）中，其他地市，特别是制造业发达地市的资本投入对本地市制造业产出的影响继续下降，为0.059，在1％水平显著，这说明模型（1）中的资本溢出效应主要发生在非邻接的制造业欠发达地市。模型（3）中，其他地市的劳动投入对本地市产出的影响在1％水平显著，这和前两个模型不同，虽然数值较小，仅为-0.075，但说明制造业发达地市的劳动力投入增加，将吸引本地市制造业工人流出而减少本地产出。模型（3）中，其他地市产业集聚对本地市产出的影响为正，但依然不显著，其他地市房价上涨能带来本地市产出增加，系数仅为0.003，但在1％水平显著。

最后，综合三个模型可发现，周边地市制造业产出对本地市制造业产出的影响均为负，但都不显著。注：括号内为t值，*,**,***分别表示10％、5％、1％显著水平。

表2　变换权重矩阵的空间杜宾模型估计结果

四、结论

综合前文的空间面板分析表明，目前山东省各地市制造业生产中：资本投入的直接效应较小，溢出效应较大，且溢出主要面向非邻接的制造业欠发达地市；无论采用何种权重衡量，劳动投入的产出弹性均远大于资本投入，且制造业劳动力为稀缺要素，一地市劳动投入增加将使其他地市制造业产出减少，这种减少在以经济活动因素衡量的权重矩阵W3中是显著的；本地产业集聚能显著促进本地制造业产出增加，对其他地市产出的影响不显著；虽然房价上涨，但房价对本地制造业产出的影响数值上非常小且统计上也不显著。

注释：

①2009年国务院批复建立黄河三角洲高效生态经济区，2011年国务院批复建立山东半岛蓝色经济区，2013年山东省确立省会城市群经济圈和西部隆起经济带，明确了“两区一圈一带”发展战略。

②这28个细分行业在“国民经济行业分类与代码（GB/4754-2011）”中对应为C13-C27，C29-C42。由于篇幅有限，平均集中率的计算结果文中并未列出，如有需要，请向作者索取。

③由于部分地市统计年鉴的统计口径差异，潍坊市以固定资产原价替代了固定资产净值，临沂市以总资产减流动资产近似估计了固定资产净值。

④年鉴中缺少威海市和滨州市2009-2011年、聊城市2011年数据，本文均通过插值法计算获得。

⑤运行结果如有需要，请向作者索取。

⑥由于篇幅有限，LR检验结果并未列出，如有需要，请向作者索取。

参考文献：

[1] Elhorst,J.P.(2003). "Specification and Estimation of Spatial Panel Data Models."International Regional Science Review 26(3):244-268.

[2] 邵挺,范剑勇.房价水平与制造业的区位分布——基于长三角的实证研究[J].中国工业经济,2010,(10):24-32.

[3] 范剑勇,李方文.中国制造业空间集聚的影响:一个综述[J].南方经济,2011,(06):53-66+6.

[4] 宋马林,王舒鸿,黄蓓,胡百红.我国中部六省产业集聚与扩散的空间计量[J].地理研究,2012,(03):534-542.

[5] 于斌斌,杨宏翔,金刚.产业集聚能提高地区经济效率吗?——基于中国城市数据的空间计量分析[J].中南财经政法大学学报,2015,(03):121-130.

[6] 徐文娟,钟立新.基于空间变换的产业集聚计量模型及实证检验[J].统计与决策,2015,(15):131-134.

[7] 唐运舒,冯南平,高登榜,杨善林.产业转移对产业集聚的影响——基于泛长三角制造业的空间面板模型分析[J].系统工程理论与实践,2014,(10):2573-2581.

[8] 谭锐,赵祥,黄亮雄.高房价下的制造业转移:城市间还是城市内?[J].经济学报,2015,(02):56-75.

[9] 李婧,谭清美,白俊红.中国区域创新生产的空间计量分析——基于静态与动态空间面板模型的实证研究[J].管理世界,2010,(07):43-55+65.

（作者单位：齐鲁工业大学金融学院）