小学数学教学中有效组织信息的策略研究

吴新江

[摘 要]学习，是一个选择信息——组织信息——整合信息的过程，其中组织信息是最为关键的步骤。通过数形结合、列表比较、转化嫁接、实践操作四个策略出发，可以促进学生有效组织信息，形成新的知识。

[关键词]小学数学 组织信息 策略 有效

[中图分类号] G623.5 [文献标识码] A [文章编号] 1007-9068（2016）05-037

组织信息是指学习者将已经选择的信息组织成一个有内在联系的整体，只有将信息与已有的知识结构建立稳定的联系时，信息才能转变成知识。那么，如何促进学生有效组织信息？笔者进行了如下策略研究。

一、数形结合策略

数形结合策略是指将抽象的数量用直观形象的图形表述出来，从而发现数学信息之间的内在联系。

如教学“比赛场次”时，教师先提出单循环制，并解释规则。

师：如果4个人采用单循环制进行比赛，需要比几场？

生1：3+2+1=6（场）。

师：能否用更简洁的方法来表达呢？

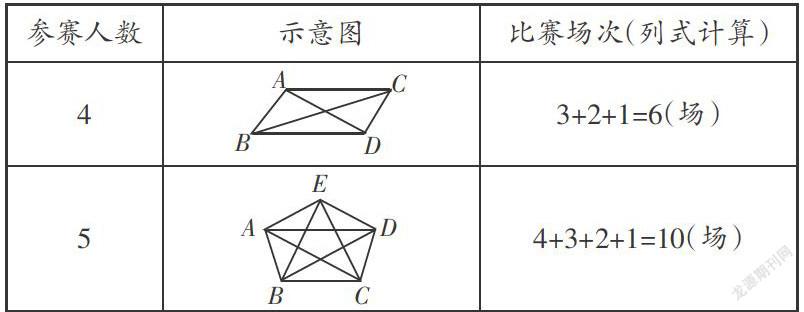
生2：可以用图示的方法。如用A、B、C、D四个点表示四位同学，然后用线连接表示比赛的场次。

（教师利用课件出示学习要求：①独立思考、完成学习单；②想一想，比赛场次与人数有什么关系？③算一算，12人一共打几场比赛？）

师：请一位同学汇报一下，并展示你的学习单。

师：请解释一下算式4+3+2+1=10的意思。

生3：4是A与B、C、D、E打的场次；3是B与C、D、E打的场次；2是C与D、E打的场次；1是D与E打的场次。

师：谁找到了单循环制的规律？请你展示出来。

生4：1+2+…+（参赛人数-1）=比赛场次。

师：还有别的规律吗？

生5：n×（n-1）÷2。

师：请你来验证，并说一说是什么意思？（板书：4×（4-1）÷2=6）

生5：如果4个人比赛，每人都要打3场，一共12场。但这样每一场都算了2遍，还要除以2，所以4个人比赛要打6个场次。

在问题比较复杂的情况下，采用数形结合策略有利于学生组织信息，从简单的情形开始，发现数量之间的一般规律。

二、列表比较策略

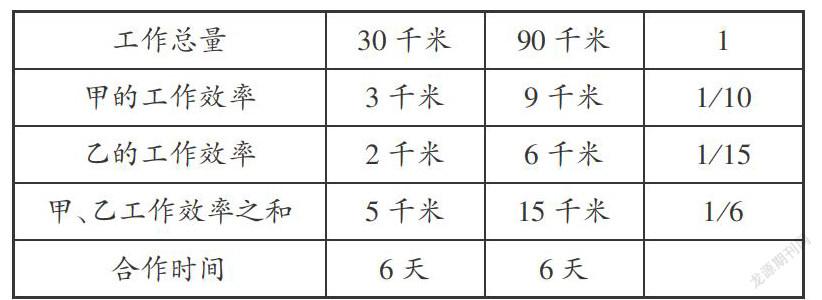
列表比较策略是指用表格把已知的信息整理出来，通过比较，发现信息内在的一致性。

如教学“工程问题”时，其关键是把工作总量看作单位“1”，工作效率用抽象的分率来表示，从而建立工作总量、工作效率与工作时间这些信息之间的联系。

1.例题：一段公路长30千米，甲队单独修10天完成，乙队单独修15天完成。两队合修几天可以完成？

2.反馈算式30÷（30÷10+30÷15），说说每一步的意思，并填表。

3.教师改变例题中的公路长为90千米，其他条件不变，让学生猜一猜两队合修几天可以完成？

4.列式解答90÷（90÷10+90÷15），并填表。

5.如果将例题中的“长30千米”去掉，怎样解答？并填表。

通过以上的列表比较，学生已经发现了工作效率与总量之间的关系，知道把工作总量看作“1”来解答，并列出算式1÷（1 / 10+1 / 15）。

学生通过观察表格，进行横向和纵向的比较，发现效率与总量的关系不变的规律，从而引出用分率来表示工作总量与效率，找到解答工程问题的一般方法。

三、转化嫁接策略

转化嫁接策略是指把新信息转化成已有的知识，并从中嫁接出与新信息之间的内在联系。

如教学“梯形的面积”时，重点是建立梯形的上底、下底、高与面积之间的内在联系。

1.出示平行四边形与三角形，并标上相应的条件，口算它们的面积。

师：我们是如何推导出平行四边形和三角形面积的计算公式的？

生：先将平行四边形或三角形转化成我们已经学过的图形，然后找出它们之间的关系，最后推导出公式。

师：这节课你们打算如何研究梯形的面积？

生：也可以把梯形先转化成已学过的图形，然后找到图形之间的联系，最后推导公式。

2.组织学生借助剪刀和若干个梯形进行研究。

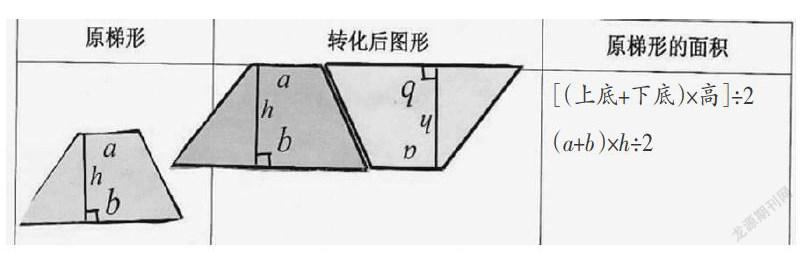
生1：我用两个梯形拼成一个平行四边形（如上图）。

师：要用两个什么样的梯形？平行四边形和梯形之间有什么关系？

生1：两个完全一样的梯形。平行四边形的底是梯形的上底加下底，平行四边形的高就是梯形的高。梯形面积就是上底加下底的和乘高除以2。

师：（a+b）×h求的是什么？为什么还要除以2？

生2：（a+b）×h是平行四边形的面积，除以2是因为这个平行四边形是两个完全一样的梯形组成的。

师：还有别的方法吗？（经过汇报交流，学生还补充了三种方法，图略）

3.组织学生对以上四种方法进行梳理，最终推导出梯形的面积计算公式。

教师要抓住原来的梯形与转化后图形之间的联系，再进行推导方法上的迁移，让学生独立探究，把新的信息转化嫁接到已有的知识中。

四、实践操作策略

实践操作策略是指通过实践操作，体验信息的具体意义，从而发现信息之间的内在联系。

如教学“长方形面积”时，关键是促使学生建立长方形的面积与长、宽之间的内在联系。

师：这个小正方形的边长是1厘米，它的面积是多少？

生：1平方厘米。

师：3×4的长方形面积是多少平方厘米？请大家估一估，再量一量，并汇报你的测量方法。

生1：我用1平方厘米的小正方形把这个长方形铺满。每行4个，可以摆3行，共12个，因此面积是12平方厘米。

生2：我是用尺量的，长4厘米，宽3厘米，4×3=12（平方厘米）。

师：算式中的4与3分别表示什么意思？

生2：4表示每行可以摆4个边长为1厘米的小正方形，3表示每列可以摆3个边长为1厘米的小正方形。

师：想一想，每行的个数与行数跟长方形有什么联系？

生3：每行的个数就是长，行数就是宽。所以长方形的面积=长×宽。

长方形的面积是二维的平面，长方形的长与宽是一维的线段，如何把二维的平面与一维的线段建立联系是教学的难点。通过实践操作，学生理解了长方形的面积、长、宽的具体意义，突破了空间思维上从一维到二维的转折。

综上所述，通过数形结合、列表比较、转化嫁接、实践操作四种策略，能够促进学生有效组织信息，帮助学生建立信息之间的内在联系，从而获得新的知识。在实际教学过程中，把这几种策略结合起来应用，效果将更加显著。

（责编 李琪琦）