高强方矩管冷弯成型角隅内侧裂纹产生原因的数值仿真分析

陈叶清骆海贺刘占增乔午锋高长华解 德　/.武汉钢铁（集团）公司研究院.华中科技大学



高强方矩管冷弯成型角隅内侧裂纹产生原因的数值仿真分析

陈叶清1骆海贺1刘占增1乔午锋2高长华2解 德2/1.武汉钢铁（集团）公司研究院2.华中科技大学

【摘 要】高强方矩管在成型生产过程中时常出现角隅内侧开裂，本文采用有限元数值模拟仿真计算，对角隅内侧裂纹产生的原因进行了研究。研究表明，角隅内侧在整个成型过程中，有因回弹引起的拉应力，且该处的等效应力-应变曲线的流动在挤压成型阶段超过了材料的真应力-应变试验曲线，超出了材料的塑性成型能力，因此在回弹拉应力的作用下产生裂纹。

【关键词】数值模拟；冷弯成型；裂纹；高强方矩管

1. 前言

随着全球节能降耗和环境保护要求的不断提高，客车轻量化已成为重要的发展趋势。采用高强度冷弯方矩管替代普通方矩管后，可以减薄壁厚，大幅降低结构自重。然而，高强钢由于具有强度高、延伸率低、变形大、成型反弹大等特点，因而在冷弯成型生产过程中以及用户的二次加工过程中时常出现开裂，而且相当一部分是在管子的角隅内侧开裂。进行高强方矩管冷弯成型数值仿真研究，有助于解释高强方矩管在成型过程中产生裂纹等缺陷的原因，以及提出降低裂纹等缺陷发生概率的工艺优化改进措施。

国内外对方矩形管冷弯成型的研究主要集中在数值仿真、成型工艺和成型缺陷等三方面。成型缺陷方面，伊朗的M.Salmani. Tehrani等[1]利用有限元数值仿真对方矩管局部屈曲进行了分析。此外，伊朗的M. Farzin等[2]借用有限元数值仿真工具，对于冷弯成型过程中屈曲应变极限的确定进行了探讨。日本小奈弘教授（Hiroshi Ona）[3]的高精度冷弯成型工艺以及缺陷的产生机理和解决方法对生产实践具有很高的指导意义。美国的B.W. Schafer等[4]讨论了考虑几何缺陷和残余应力情况下冷弯型钢的计算模型。从国内外公开的相关文献可以看出，在成型缺陷方面只涉及到对屈曲等缺陷数值仿真的讨论，基本上没有涉及对矩形管裂纹产生原因和预防进行讨论，更谈不上应用工厂的实际生产案例。

本文针对客车用高强方矩管在冷弯成型过程中角隅内侧产生裂纹的现象，开展冷弯成型过程中的数值仿真研究，通过仿真模型分析裂纹产生的原因。

2. 数值仿真模型的建立及计算

高强方矩管冷弯成型数值仿真模型的确立主要根据高强方矩管的实际生产工艺流程来确定，研究模型采用的是规格40×40×1.5mm的四四二次弯边成型方矩管。

有限元模型的建立利用Femap软件，计算仿真利用以擅长处理非线性和复杂接触问题著称的ABAQUS高级有限元仿真软件。计算方法采用二维有限元数值仿真分析方法，能完整地仿真整个冷弯成型流程，且能方便地分析冷弯成型过程中的大塑性变形和回弹等成型基本现象。尤其对容易产生裂纹的角隅处，能方便地对其进行细节分析。

在角隅外侧，整个高强方矩管冷弯成型过程中，以外圆弧处塑性应变较大的4062号单元作为典型节点读出该点处每个成型道次回弹前和回弹后的应力，绘制出应力谱。同理，在角隅内侧，整个高强方矩管冷弯成型过程中，以内圆弧处塑性应变较大的62号单元作为典型节点读出该点处每个成型道次回弹前和回弹后的应力，绘制出应力谱。

在角隅外侧，4062号单元的等效应力-应变曲线（εe− σe曲线）沿材料真应力-应变曲线（ε−σ曲线）的流动如图1所示。在角隅内侧， 62号单元的等效应力-应变曲线（εe− σe曲线）沿材料真应力-应变曲线（ε−σ曲线）的流动如图2所示。

图1

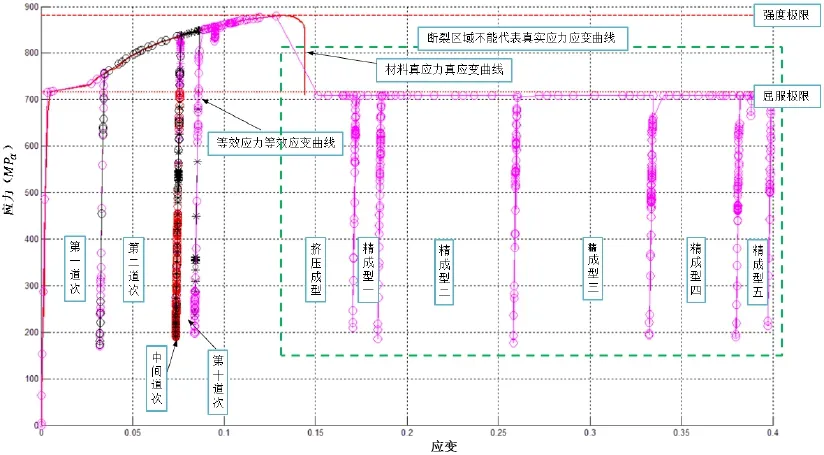
图2

3. 分析与讨论

关键节点处产生裂纹的原因必须满足两个条件：一是εe− σe曲线的流动超过材料的ε−σ曲线；二是该关键节点处存在拉应力。

从图1和图2可以看出，在高强方矩管整个冷弯成型过程中，角隅外侧和角隅内侧的应力谱特点表现为：在成型、挤压和精整阶段都存在拉压交变应力。对于角隅外侧的4062号关键节点，虽然该点存在拉应力，但是εe− σe曲线流动并没有超过材料ε−σ曲线，因此该节点处于安全状态，即不产生裂纹；对于角隅内侧的62号关键节点， εe− σe曲线流动在挤压道次超过材料ε−σ曲线，而且该点在挤压成型阶段及以后的道次，存在拉应力，因此该节点产生裂纹。实际生产高强方矩管过程中，角隅外侧安全，内侧破裂产生裂纹，且裂纹由内向外扩展，与数值模拟仿真计算的结果一致。

4. 结 论

数值仿真计算结果表明：角隅外侧虽然存在拉应力，但是该处的等效应力-应变曲线的流动在整个成型阶段没有超过材料的真应力-应变试验曲线，材料的塑性成型能力还保留着，能抵抗该处的拉应力。因此，角隅外侧不产生裂纹。而角隅内侧在整个成型过程中，有因回弹引起的拉应力，且该处的等效应力-应变曲线的流动在挤压成型阶段超过了材料的真应力-应变试验曲线，超出了材料的塑性成型能力，失去抵抗外力作用下变形的能力，因此在回弹拉应力的作用下产生裂纹。

参考文献：

[1]M.Salmani.Tehrani，P. Hartley，H. Moslemi Naeini，H. Khademizadeh. Localised edge buckling in cold roll-f orming of symmetric channel section[J]. Thin-Walled Structures，2006，44：184-196.

[2]M. Fa rzin，M. Sa lmani Tehrani，E. Shameli，Determination of buckling lim it of s train in cold roll form ing by the finite elem ent analysis[J]. Journal of Materials Processing Technology，2002，125（126）：626-632.

[3]小奈弘，刘继英. 冷弯成型技术[M]. 北京：化学工业出版社，2007.

[4]B.W. Schafer，T. Peko¨z. Computational modeling of coldformed steel: characterizing geometric imperfections a nd residual stresses[J]. Journal of Constructional Steel Re search，1998，47：193-210.