基于数据驱动与信息增益率多指标决策模型的生活饮用水水质评估

李 佳 龙，　阎 威 武*，　白 晓 慧，　邵 惠 鹤

( 1.上海交通大学 电子信息与电气工程学院， 上海　200240；

2.上海交通大学 生命科学技术学院， 上海　200240 )



基于数据驱动与信息增益率多指标决策模型的生活饮用水水质评估

李 佳 龙1，阎 威 武*1，白 晓 慧2，邵 惠 鹤1

( 1.上海交通大学 电子信息与电气工程学院， 上海200240；

2.上海交通大学 生命科学技术学院， 上海200240 )

摘要：生活饮用水的水质情况对于居民的日常生活非常重要．建立一种基于数据驱动与信息增益率的多指标决策模型来评估生活饮用水的水质．该决策模型首先通过变异系数法对多指标系统的每个指标赋予初始权重，然后通过综合加权指数评价方法得到初始的评价结果，最后应用信息增益法根据各指标贡献度调整权重后再次评估系统．该模型不仅可以综合评估生活饮用水的水质，也可以找到对评价结果起关键作用的重要指标．通过GIS直观展示了水质分布情况，说明该决策模型的有效性．

关键词：生活饮用水；数据驱动；变异系数；信息增益率；GIS

0引言

随着生物检测技术与微量分析技术的进步，人们对饮用水中某些危害元素的认识逐步深化，同时世界卫生组织以及各国的卫生机构都不断修订水质标准[1]．近年来，研究者对于地表水和河流水的水质研究较多，对于生活饮用水的水质研究较少．生活饮用水系统是一个多指标的复杂系统，对水质的综合评估属于多指标决策问题．多指标决策问题存在于人类社会的各个领域，多指标决策方法也一直是系统分析者所研究的课题[2]．这类问题通常需要用到综合评估系统，而系统中包含多指标、多层次，对系统客观合理的综合评估通常比较困难．多指标系统的评估通常采用基于各指标权重的方法，包括主观权重法和客观权重法．比较常见的主观权重法包括层次分析法[3-5]和专家评估法[6]等．主观权重法虽然能够根据领域专家的经验得到一定的信息，但脱离实际数据，且由于一定的主观性易造成综合评估的偏差．客观权重法包括熵权法[7]、变异系数法[8-9]和主元分析法[10]等，其依赖于历史数据，评价多指标决策系统通常采用单一的客观权重法，这样求取权重过程过于简单，鲁棒性不够，很可能会被噪声数据所干扰，造成所得到的客观权重信息丢失，与实际情况产生偏差．

信息增益是基于信息理论的[11]．在信息理论中，熵是一个非常重要的概念，表示任何一种能量在空间中分布的均匀程度，能量分布越不均匀，越不确定，熵就越大．信息熵是信息的量化度量，用以衡量一个随机变量取值的不确定性程度[12]．信息增益已经应用在文本分类中[13]．该方法能够重新得到每个指标对于系统的重要程度，其一方面可以用来指导数据采集过程，为这些指标的分析与确定提供理论上的支持；另一方面也可以用来对检测指标进行约简[14]．信息增益率是对信息增益的改进，其削弱了信息增益倾向取值较多的属性的缺点．

变异系数法根据数据离散程度计算多指标系统中各个指标在系统中的权重，离散程度越大权重越大，这种算法过于简单，对历史数据的信息挖掘不够充分．

本文对生活饮用水水质综合评估问题进行深入研究，并验证所提出的综合变异参数法、综合加权指数法和信息增益率的多指标决策模型的效果，为综合评估多指标系统提供一种有效途径．

1多指标决策模型

多指标决策模型通过变异系数法计算得到系统中各指标权重，通过综合加权指数法打分得到评价等级，然后采用信息增益率方法对权重进行调整，最后再次通过综合加权指数法进行综合评分得到系统的综合评价结果．

1.1变异系数法

变异系数法是用来检测样本数据离散程度的一种常用的统计方法．这种方法能够根据数据离散程度计算多指标系统中各个指标在系统中的权重．基本的理论是：在多指标决策评估系统中，某指标的样本数据表现得越不同，越能更好地反映综合评估效果，因此应该被赋予更大权重．

变异系数法共有4个计算步骤[15]：

(1)对于一个评估矩阵X=(xij)m×n，m代表待评估系统中历史数据样本的数量，n代表指标的数量，由于不同指标对应的值有不同的数量级，数据应该归一化以消除数量级差异的影响．被归一化后的矩阵为Z=(zij)m×n，其中

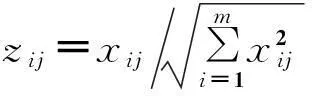
(1)

(2)计算标准化矩阵Z的均值和标准差：

(2)

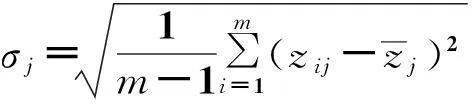
(3)

(3)得到变异系数：

(4)

(4)根据各指标变异系数得到指标的权重：

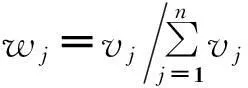
(5)

以上4步是变异系数法对历史数据中各指标权重的求解过程．

1.2信息增益理论

通常来说，变异系数法完全依据历史数据，具有一定的不稳定性，因此采用信息增益率对权重进行调整．

特征t的信息增益定义如下：

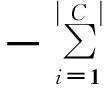
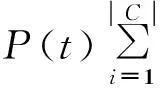
(6)

本文根据决策树C4.5对信息增益做了进一步的改进，由于信息增益偏向于取值比较多的属性，需要用信息增益除以一个分裂信息度量来得到各指标的信息增益率削弱这种作用．

1.3综合加权指数评价法

综合加权指数评价法是一个实用而且可靠的评价方法，它采用一系列权重与各指标评分加权和作为综合标准来评价一个多指标的决策系统[16]．由于本文应用于生活饮用水的综合评估，按照评价生活饮用水定义进行指标评分，具体的计算方法如下：

(1)单指标的计算

单指标计算公式如下：

(7)

式中：Ii为第i个评价指标的分值；Ci为第i个评价指标的实测结果；Si,k为第i个评价指标的k级标准浓度；Si,k+1为第i个评价指标的k+1级标准浓度；Ii,k为第i个评价指标的k级分数，取值如表1所示．

表1　评价指标分级分数

(2)综合指标的计算

当各指标的权重与分数得到后，综合评分计算公式如下：

(8)

生活饮用水根据综合评分的类别划分如表2所示．

表2　生活饮用水各类别的分数区间

1.4多指标决策模型建模过程

对于一个多指标系统，用合理的方式做综合评估来指引决策是很有意义的事．变异系数法是基于样本数据的一种客观求权重方法，然而完全依照数据的离散程度来确定指标权重是单一片面的，本文提出采用信息增益法来调整指标的权重．由于信息增益需要提前知道样本的标签即类别，在调整权重之前，需要用综合加权指数评价法对系统的样本数据进行评价并赋予类别，然后采用信息增益法对指标的权重进行重新调整计算．

多指标决策模型的过程建模如下．

首先历史数据用矩阵X来表示：

(9)

矩阵中，m代表样本的数量，n代表指标的数量．通过上述的变异系数法可以得到指标权重为wA=(w1w2…wn)T．

然后根据综合加权指数评价法获得每条历史样本数据的综合评分．

根据信息增益法[17]，已知X为样本数据，初始标签即类别，假设经过综合评价后多指标决策系统共有k个等级ci(i=1,2,…,k)，样本的期望信息为

(10)

式中：si是属于类别ci的样本数目，p(ci)是根据样本数据取第i等级的概率．

每个指标的信息熵为

(11)

式中：A代表某个指标；v是该指标属于不同类别的数目，同时将样本数据划分为v个不同的子集；si,j代表在子集sj中属于ci类别的数目，s为样本总数；I′(s1,s2,…,sk)代表在子集sj中A指标的期望信息．

因此A指标的信息增益

G(A)=I(s1,s2,…,sk)-E(A)

(12)

通过G(A)可以得到各个指标的信息增益G(X)=(g1,g2,…,gn)，其中X=(x1x2…xn)，代表n个指标．然后根据下式计算各个指标的信息增益率：

(13)

其中G(X)是各指标的信息增益，H(X)是各指标的分裂信息度量．

(14)

其中k代表某个属性的类别数，p(xi)为在所有样本中某属性取各个类别的概率．

然后将信息增益率归一化可以得到各指标的权重u=(u1u2…un)T．

最后再次使用综合加权指数评价法根据调整后的权重对多指标决策系统进行综合评分．

该多指标决策模型不仅可以有效评价一个系统，而且可以找到系统中关键指标，对于维度很高的多指标系统，可以起到降维的作用．

2结果与分析

2.1应用背景

生活饮用水综合评估系统构成了一个多指标决策评估系统．上海管网水的综合水质需要每个月进行评估．根据世界卫生组织和我国生活饮用水卫生标准，对管网水的综合评估主要针对6项非常重要的指标，分别为菌落总数、色度、浑浊度、耗氧量、锰和余氯．

文中选取2012年的历史数据作为样本数据，分别定义I1、I2、I3、I4、I5和I6为菌落总数、色度、浑浊度、耗氧量、锰和余氯，L代表管网水水质等级．

2.2多指标决策模型的应用过程

对于管网水的各项指标，根据《生活饮用水卫生标准》(GB 5749—2006)的等级划分范围如表3所示．首先，通过变异系数法计算6项管网水指标的初始权重，结果计入表4，然后用前文的综合加权指数评价法得到综合评分，进而根据表2确定每个样本数据赋予初始等级．

表3　生活饮用水等级划分

表4变异系数法得到的各指标权重以及经过信息增益调整后的各指标权重

Tab.4Weightsofindicesthroughvariationcoefficientmethodandadjustedbyinformationgain

指标信息增益信息增益率信息增益率归一化的权重变异系数法权重菌落总数0.0520.2490.2510.309色度0.0220.0300.0300.036浑浊度0.0470.0330.0340.039耗氧量0.8870.5290.5330.520锰0.2060.1370.1380.047余氯0.0200.0140.0140.049

余氯指标根据综合加权指数法打分方法较为特殊，优、良的标准范围一样，差、劣的标准范围也一样，因此该指标计算时只取优或差．

在得到了有初始等级的样本数据后，信息增益率将被应用于对各指标权重的调整．

样本的期望信息可以通过式(10)得到：

I(L)=1.242 8

对于单个指标菌落总数，其熵可以通过式(11)得到：

E(I1)=1.190 3

根据式(12)可以得到菌落总数的信息增益：

G(I1)=1.242 8-1.190 3≈0.052

其余5项指标的信息增益用相同的方法求得：

得到各指标的信息增益后计算各指标的信息增益率．以菌落总数为例，根据式(14)计算菌落总数的分裂信息度量为

H(I1)=0.209

然后通过式(13)可得菌落总数的信息增益率：

Rg(I1)=0.249

同理可得其余指标的信息增益率．将各指标的信息增益率归一化得到调整后的权重，结果见表4．

2.3实验结果与讨论

经过2.2对于多指标决策模型在生活饮用水系统的应用，得到表4各指标由变异系数法得到的初始权重、信息增益调整后的权重．

从表4结果可以看到通过变异系数法得到的菌落总数与耗氧量的权重很高，说明这两项指标数据波动较大，离散程度高．经过信息增益调整后，锰的权重有了显著提高，耗氧量的权重进一步提高，这说明锰和耗氧量对于管网水水质的综合评价具有突出的贡献．信息增益调整后，菌落总数的权重大大降低，通过分析数据可知，菌落总数绝大多数的取值集中在优，数据较集中，菌落总数数据的特点导致其取值单一倾向于优，而信息增益倾向于取值较多的属性，因此信息增益较小；分裂信息度量削弱了信息增益的这种作用，使菌落总数的信息增益率比较高．变异系数法得到权重后，经过信息增益率的调整，挖掘出锰这项关键指标，菌落总数和耗氧量依然为重要指标．最终重要指标被确定为菌落总数、锰和耗氧量．

为了进一步验证菌落总数、锰和耗氧量是否为关键指标，同时更直观地观测水质情况，运用GIS展示 2012年某月上海市管网水的分布图．两幅地图采用的是Kriging插值方法[18]．使用全部指标以及调整后的权重并通过综合加权指数法得到各个监测点的水质评分，得到了图1所示的管网水水质分布图．只用菌落总数、锰和耗氧量3项指标以及调整后的权重并通过综合加权指数法得到了图2所示的水质分布图．通过底层数据比较，可以发现在215个监测点中，有211个监测点的最终综合水质等级相同，综合评价的相似度达到98.1%．可以看到水质分布趋势非常相似，地图右下角已说明，绿色越深代表水质越好，黄色为合格水，橙色代表较差水质，红色代表劣质水．且水质分布层次均匀分明，符合客观事实，说明了该多指标决策模型的有效性和可行性．

图1　6项指标综合评价的水质分布图

图2　关键指标综合评价的水质分布图

3结语

本文提出一种基于数据驱动与信息增益率的多指标决策模型，应用于上海生活饮用水的水质综合评估，并通过GIS作图在空间上予以展示，结果表明通过该多指标决策模型得到的综合饮用水水质分布情况符合客观事实，同时对关键指标的提取比较可靠．由于生活饮用水评价系统和其他多指标决策评估系统比较复杂，涉及的信息繁杂，综合评价往往不是一种模型可以解决的，本文的多指标决策模型提供了一种可行方案．在将来的决策模型研究中，可以考虑其他的评估方法，同时在线更新历史数据来实时调整指标的权重．

参考文献：

[1]李崇善,郭 明,马成雄. 我国生活饮用水卫生标准发展研究[J]. 甘肃科技, 2012, 28(21):55-59.

LI Chong-shan, GUO Ming, MA Cheng-xiong. The research of domestic drinking water hygiene standards development [J]. Gansu Science and Technology, 2012, 28(21):55-59. (in Chinese)

[2]黄德成. 对指标带有偏好的多阶段多指标决策[J]. 运筹与管理, 2001, 10(2):42-46.

HUANG De-cheng. The multi-stage and multiple attribute decision-making with the favouritism for the index [J]. Operations Research and Management Science, 2001, 10(2):42-46. (in Chinese)

[3]Kwong C K, Bai H. A fuzzy AHP approach to the determination of importance weights of customer requirements in quality function deployment [J]. Journal of Intelligent Manufacturing, 2002, 13(5):367-377.

[4]Lin Ming-chyuan, Wang Chen-cheng, Chen Ming-shi,etal. Using AHP and TOPSIS approaches in customer-driven product design process [J]. Computers in Industry, 2008, 59(1):17-31.

[5]Lu M H, Madu C N, Kuei C-H,etal. Integrating QFD, AHP and benchmarking in strategic marketing [J]. Journal of Business & Industrial Marketing, 1994, 9(1):41-50.

[6]曲丽丽,康 锐. 研制阶段装备保障方案的专家评分评价法[J]. 兵工自动化, 2009, 28(6):17-19.

QU Li-li, KANG Rui. Expert evaluation method for equipment support scheme during development [J]. Ordnance Industry Automation, 2009, 28(6):17-19. (in Chinese)

[7]ZOU Zhi-hong, YUN Yi, SUN Jing-nan. Entropy method for determination of weight of evaluating indicators in fuzzy synthetic evaluation for water quality assessment [J]. Journal of Environmental Sciences, 2006, 18(5):1020-1023.

[8]CHEN Wei, HAO Xiao-hong. An optimal combination weights method considering both subjective and objective weight information in power quality evaluation [J]. Lecture Notes in Electrical Engineering, 2011, 87(2):97-105.

[9]Breusch T S, Pagan A R. A simple test for heteroscedasticity and random coefficient variation [J]. Econometrica, 1979, 47(5):1287-1294.

[10]Dalal S G, Shirodkar P V, Jagtap T G,etal. Evaluation of significant sources influencing the variation of water quality of Kandla creek, Gulf of Katchchh, using PCA [J]. Environmental Monitoring and Assessment, 2010, 163(1):49-56.

[11]Fan R, Zhong M, Wang S,etal. Entropy-based information gain approaches to detect and to characterize gene-gene and gene-environment interactions/Correlations of complex diseases [J]. Genet Epidemiology, 2011, 35(7):706-721.

[12]Harte J, Newman E A. Maximum information entropy:a foundation for ecological theory [J]. Trends in Ecology & Evolution, 2014, 29(7):384-389.

[13]Rajeswari K, Sneha Nakil, Neha Patil,etal. Text categorization optimization by a hybrid approach using multiple feature selection and feature extraction methods [J]. Engineering Research and Applications, 2014, 4(5):86-90.

[14]史志才,夏永祥. 基于知识约简的网络入侵特征提取[J]. 计算机工程, 2011, 37(5):134-136.

SHI Zhi-cai, XIA Yong-xiang. Network intrusion feature extraction based on knowledge reduction [J]. Computer Engineering, 2011, 37(5):134-136. (in Chinese)

[15]Weber E U, Shafir S, Blais A-R. Predicting risk sensitivity in humans and lower animals:risk as variance or coefficient of variation [J]. Psychological Review, 2004, 111(2):430-445.

[16]Dawoud A, Alam M S. Target tracking in infrared imagery using weighted composite reference function-based decision fusion [J]. IEEE Transactions on Image Processing, 2006, 15(2):404-410.

[17]杨光明,杨 坤,黄 勇,等. 基于信息增益的水工金属结构健康诊断赋权方法研究[J]. 水力发电学报, 2014, 33(3):253-257.

YANG Guang-ming, YANG Kun, HUANG Yong,etal. Research on weight method for hydraulic metal structure health diagnosis based on information gain [J]. Journal of Hydroelectric Engineering, 2014, 33(3):253-257. (in Chinese)

[18]Lee K H, Kang D H. Structural optimization of an automotive door using the Kriging interpolation method [J]. Journal of Automobile Engineering, 2007, 221(12):1525-1534.

Multiple criteria decision-making model based on data driven and information gain ratio for drinking water quality evaluation

LIJia-long1,YANWei-wu*1,BAIXiao-hui2,SHAOHui-he1

( 1.School of Electronic Information and Electrical Engineering, Shanghai Jiao Tong University, Shanghai 200240, China；2.School of Life Sciences and Biotechnology, Shanghai Jiao Tong University, Shanghai 200240, China )

Abstract：The drinking water quality is important for residents′ daily life, so a multiple criteria decision-making model based on data driven and information gain ratio is set up to evaluate drinking water quality. Firstly, the initial weights of every index in multiple indices system are determined by the variation coefficient method. Secondly, the initial evaluation results are obtained by the comprehensive weighted indices evaluation method. Finally, information gain method is applied to adjust the weights of indices according to the contribution degree and evaluate the system again. The model can not only comprehensively evaluate the drinking water quality, but also find the important indices playing a key role. Water quality distribution is shown intuitively by GIS to illustrate the validity of the decision-making model.

Key words：drinking water; data driven; variation coefficient; information gain ratio; GIS

作者简介:李佳龙(1990-)，男，硕士，E-mail:li_jia_long_1990@163.com；阎威武*(1971-)，男，副教授，E-mail:yanwwsjtu@sjtu.edu.cn.

基金项目:国家自然科学基金资助项目(60974119).

收稿日期：2015-08-10；修回日期: 2015-11-20．

中图分类号：N94

文献标识码：A

doi:10.7511/dllgxb201601014

文章编号：1000-8608(2016)01-0092-06