基于线性规划的产品宣传媒介的选择和排期的研究
霍俊爽+朱翠娟+张若东+邰志艳+王柳行


摘要 本文主要基于线性规划理论分析和研究了产品宣传时对电视、互联网、广播、报纸等广告媒介的选择以及排期等方面的问题。首先应用统计学方面的理论分析得出了媒介的选择范围与效果预估,然后基于线性规划理论进行了求解。
关键词 线性规划;统计分析;产品宣传;媒介
中图分类号022 文献标识码A 文章编号1674-6708(2015) 153-0018-01
企业产品的广告宣传效应的好坏直接影响了产品的销售量,企业的管理者更期望所花费的广告费的宣传效应达到最大化,因此在产品宣传时,广告媒介的选择和排期等方面必须进行优化。本文基于线性规划理论对产品宣传媒介的选择和排期的研究。
1 基本理论
1.1 线性规划
定义1:-般地,把具有:1)用一组变量x,屯,L,%的每取一组不同的非负值表示一个不同的具体方案,取值可由决策者进行决定,所以把蕾,屯,L,%称为决策变量;2)都有一个用未知变量的线性函数表示的目标要求,要求对该线性函数求最大或最小,一般把目标要求称为目标函数;3)都有用一组线性等式或不等式表示的一组约束条件,决策变量的取值受到这组约束条件的约束,称这组线性等式或不等式为约束条件。我们把这类问题称为线性规划问题。
1.2 线性规划的求解
线性规划问题求解方法主要有:1)图解法,对有两个决策变量的线性规划进行求解可以使用该方法,主要是利用直角坐标系绘制出解的可行域,然后找到使目标函数达到最优的解;2)单纯形法,主要是利用单纯形表进行求解;3)软件求解,常用的优化软件有LINDO和LINGO等。
2 产品宣传媒介的选择和排期的实证研究
2.1 宣传媒介情况的统计调查与分析
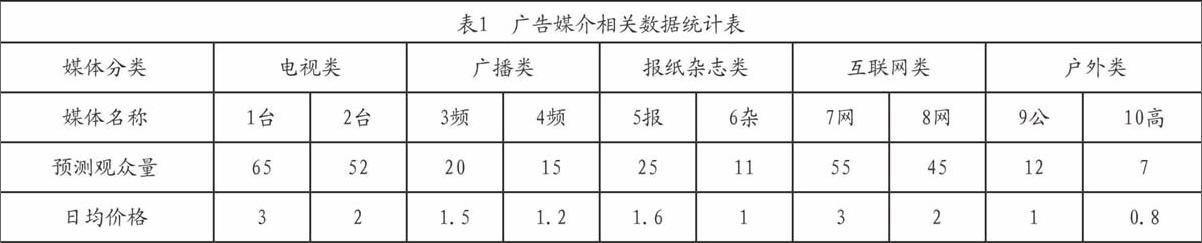
某公司为其一款新产品上市制定了宣传计划,宣传期在媒体上总投放广告宣传费用100万元,根据调查了解了各广告媒介的日均观众量(万次)和日均价格(万元)等相关数据。现管理层要求,电视类媒介投放的费用不超过30万元,广播类媒介投放的费用比例不低于总投放的15%,互联网类媒介观众量要达到700万次,户外类媒介投放的费用比例不高于总投放的10%,每个媒体分类至少宣传5天,每个媒介宣传的时间都不能超过20天。求满足约束条件的各个宣传媒介投放天数,让媒介总的观众量最大化。
2.2 宣传媒介选择与排期的线性规划模型
设表1中从左到右的各个广告宣传媒体的投放天数分别为X1,x:,L,X1。,媒体总的观众量用z表示,则有如下数学模型:
2.3 模型求解
该模型的求解可以使用单纯形法,但由于有12个变量,所以计算量比较大,因此该问题使用LINDO或LINGO软件求解,利用LINDO软件求得模型最优解为(五,%,X,X4,x5,X,玛,xs,玛,X10)=(0,15,10,0,4,1,l,20,3,2),目标函数最优值为2 096万次。所以求得到该次广告投放的具体媒体及相应的天数为电视类2台宣传时间为15天、广播类3频宣传时间为10天、报纸杂志类5报宣传时间为4天、报纸杂志类6杂宣传时间为1天、互联网类7网宣传时间为1天、互联网类8网宣传时间为20天、户外类9公宣传时间为3天、户外类10高宣传时间为2天,可以使总观众量达到最大2096万次。
3 结论
求解这类问题时使用线性规划理论能够快速的求得相应结果,若只有两个变量时可用图解法求解,但一旦遇到较多当变量时使用LINDO或LINGO软件求解更容易。产品宣传媒介的选择和排期方面的研究,通过使用线性规划理论使之达到了最优。

