均值不等式的应用与实践

赵 秀

(兴义民族师范学院数学科学学院，贵州 兴义 562400)

均值不等式的应用与实践

赵 秀

(兴义民族师范学院数学科学学院，贵州 兴义 562400)

均值不等式是不等式的一种特殊种类，在不等式之中处于核心地位，在解题及现实生活中有着广泛的应用，也是高考中的一个重点。通过分析均值不等式的应用与实践，对学生逻辑思维能力及实践能力的培养有重要意义。

均值不等式；应用；实践

1 均值不等式及其推广

1.1 均值不等式

1.2 均值不等式推广(推广到有限个正数)

注意①ai>0,i=1,2,…n；

③当且仅当a1=a2=…=an时，等式成立。

总结：一正二定三相等。

2 均值不等式在解题中的应用

2.1 用均值不等式求极限

解：由n元均值不等式，有

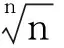
2.2 用均值不等式求最值

例2，已知2b2-a2=1，求y=|a-2b|的最小值。

当且仅当a=b,2b2-a2=1,即a=b=1或a=b=-1时，y的最小值为1。

2.3 用均值不等式求函数值域

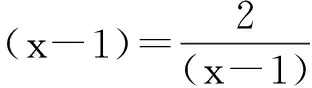
2.4 用均值不等式比较大小

解：根据题意，可由均值不等式，得：

即，Q>P，

即 R>Q。

由于a>b，所以a≠b，所以不能取等号，

即 R>Q>P。

3 均值不等式在现实生活中的实践应用

罗丹曾说过：生活不是缺少美，只是缺少发现美的眼睛。这句话同样适用于数学，生活中不是缺少均值不等式的应用，只是缺少我们的细心观察。数学源于生活，又高于生活，均值不等式在生活中有着广泛的应用，例如，在机械铸造、建设投资、商品销售等问题上都有均值不等式的身影。

3.1 运用均值不等式，解决机械铸造问题

例5，用一块钢锭浇铸一个厚度均匀，且全面积为2m2的正四棱锥形有盖容器，设容器高为h(m)，盖子边长为a(m)。

1)求a关于h的函数解析式；

2)设容器的容积为V,则当a为何值时，V最大，求最大值。

3.2 运用均值不等式，解决建设投资问题

例6，某单位决定投资3 200元建一仓库(长方体状)，高度恒定，它的后墙利用旧墙不花钱，正面用铁栏，每1m长造价40元，两侧墙砌砖，每1m长造价45元，顶部每1m2造价20元。计算：

1)仓库底面积S的最大允许值是多少？

2)为使S达到最大，而实际投资又不超过预算，那么正面铁栏应设计为多长？

解：设铁栏长为xm，一堵砖墙长为ym，则有S=xy。

由题意得：40x+2×45y+20xy=3200

应用算术平均数与几何平均数定理，得：

从而S≤100.

因此，S的最大允许值是100 m2，取得此最大值的条件是40x=90y，而xy=100，由此求得x=15，即铁栏的长应是15m。

4 结语

处理均值不等式在解决实际应用问题应该按照以下几点要求进行：

第一，读题和审题，读题时要对题目的条件及要求有个粗略的了解，形成框架，审题时要明确题目的各个条件(包括隐含条件)，明确求解。第二，审完题后，设出变量，建立数学模型，即抽象出函数关系式。第三，在该问题有意义的自变量的取值范围内(即定义域)，求出问题的解。第四，从数学模型之中还原到实际问题之中，写出实际问题的解法和解答过程。

Application and practice of mean value inequality

ZHAO Xiu

(School of Mathematical Sciences, Xingyi Normal University for Nationalities, Xingyi 562400, China)

Mean value inequality is a special kind of inequality, which is in the core position in the inequality. It is widely used in solving problems and real life, and it is also a key point in the college entrance examination. This paper analyzes the application and practice of mean value inequality, which has important significance to the cultivation of students′ ability of thinking and practical ability.

Mean value inequality; Application; Practice

2016-10-09

赵秀(1967-)，女，学士，副教授。

G634.6

B

1674-8646(2016)23-0025-02