雷达跟踪海上低空目标仰角误差计算方法研究

曹淑艳 王红光 董翔

(1.92941部队96分队,葫芦岛 125000;2.中国电波传播研究所,青岛 266107)

雷达跟踪海上低空目标仰角误差计算方法研究

曹淑艳1王红光2董翔2

(1.92941部队96分队,葫芦岛 125000;2.中国电波传播研究所,青岛 266107)

针对雷达跟踪低空目标受传播环境影响的仰角误差问题,基于电磁波传播的抛物方程方法,提出一种能计算多路径和大气折射等造成低仰角误差的新方法．正常大气折射条件下,与射线方法结果的对比显示了该方法的正确性．利用所提方法,仿真分析了粗糙海面、大气波导等不同环境条件下的雷达测角误差,并仿真了采用窄角和偏轴跟踪方式减轻多路径效应后的改善效果．计算过程和仿真结果表明,所提方法可同时考虑大气波导和多路径等复杂传播环境的综合影响,以及雷达参数和工作方式等因素的共同影响．

大气波导;多路径;抛物方程;低仰角跟踪

引 言

雷达跟踪探测海上低空目标时,雷达波受到海面反射和大气折射等传播效应的影响,导致仰角测量误差较大且变化较复杂[1]．由于海面的反射,雷达和目标之间的电波传播存在多条路径,会造成较大的仰角误差．另外,由于大气波导等大气折射环境的存在,仰角误差还受到折射效应影响．一般情况下,随着仰角的降低,仰角误差增大．研究表明,仰角误差并不是多路径误差和大气折射误差的简单叠加．大气折射会改变多路径参数,对仰角误差造成复杂的影响[2]．近几十年,国内外研究人员一直在雷达低仰角跟踪方面开展研究,主要是针对多路径效应,提出不少减轻多路径影响的方法,如采用窄波束天线,利用最大似然估计等信号处理技术,用来改善仰角测量精度[3-4]．在仰角误差计算方面,基于射线追踪技术,形成可模拟低仰角误差的计算方法[2]．但当海上存在大气波导时,由于聚焦和散焦效应,该方法无法计算仰角接近于零度时的误差．抛物方程(Parabolic Equation, PE)由波动方程近似得到,可考虑电磁波传播的折射、反射、绕射等效应,特别适于求解大气波导等复杂环境中的远距离无线电传播问题[5-6]．结合雷达测角原理,可采用抛物方程模拟计算仰角误差[7]．本文给出基于抛物方程的极低仰角情况下误差计算方法,并进行了仿真计算和分析,可为雷达低仰角跟踪试验数据分析和误差修正提供参考．

1 基于抛物方程计算测角误差

跟踪雷达普遍单脉冲测角方法,该方法通过比较两个或多个天线波束同时接收到的目标回波信号幅度,获得目标角度位置信息．PE根据初始场计算下一距离处电场或磁场强度,最终获得整个距离-高度计算区域的场强分布情况．初始场可根据天线方向图计算获得．

1.1 单脉冲测角误差

采用单脉冲测角的雷达,一般在俯仰方向上发射两个相同且彼此部分重叠的窄波束[8],这里用波束1、波束2分别表示．波束1、波束2之间的指向偏差为固定值．两波束中间指向称为天线视轴方向,是两波束和信号最大值的指向．具有相同形状的波束1、波束2天线功率方向图分别表示为:

f1(θ)=f(θ+θk);

(1)

f2(θ)=f(θ-θk) .

(2)

式中:θ为目标偏离天线视轴方向的角度;θk为两波束指向偏离视轴方向的偏置角度．

目标回波被两天线分别接收,由其信号功率和差之比得到误差信号

(3)

利用雷达天线方向图和偏置角,根据式(3),可制作出根据Δ/Σ得到目标偏离天线视轴方向角度θ的查找表或函数关系,表示为

(4)

式中xT、hT表示目标的距离和高度位置．目标视在仰角(雷达测量角度)则为

θA(xT,hT)=θs-θ(xT,hT).

(5)

式中θs是天线视轴的指向．

在仿真计算中,根据目标与雷达的位置关系,易计算得到目标几何仰角,则根据视在仰角和几何仰角θT,最终目标仰角误差为

θe(xT,hT)=θT(xT,hT)-θA(xT,hT).

(6)

1.2 回波信号幅度的计算

根据式(3)～(6)可知,计算仰角误差的关键是分别计算出两波束接收的目标回波强度．

雷达分别通过波束1和波束2接收目标散射回波,利用抛物方程方法计算得到雷达至目标的路径传播损耗L1(xT,hT)和L2(xT,hT)(考虑天线方向图影响),则目标回波功率分别为:

(7)

(8)

式中K是与雷达发射功率、目标RCS等参数相关的量,对两天线等价．

则目标回波误差信号可表示为

(9)

设电磁波沿海面朝x轴正向传播,z为高度,采用宽角算子的抛物方程形式如下[9]:

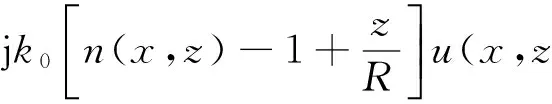
(10)

式中:u(x,z)表示场强;k0表示电磁波波数;R是地球半径．

海面采用Lenotovich阻抗边界条件

∂u/∂z+αu=0.

(11)

式中a为阻抗参数。在此边界条件下，PE的混合傅里叶变换数值解形式为

(12)

式中:n(x,z)是位置(x,z)处的大气折射指数,FS和FC分别表示正弦和余弦变换,其中:

pcos(pz)]dz;

(13)

(14)

由式(12)～(13)容易看出,电磁波场强的空间分布可根据初始场沿x方向步进求解得到．大气折射效应由大气折射指数体现,海面反射效应由阻抗边界条件反映．路径损耗L(dB)由场强根据式(15)得到

L(x,z)=20lnf+10lnr-20lnu(x,z)-27.6

(15)

式中:f为频率,MHz;r为距离,m.

传播路径上存在岛屿等不规则地形情况下,可采用双向抛物方程法计算场强分布[10-12],基于该方法的仰角误差分析拟作为后续进一步的研究内容,本文不再展开论述．

2 测角误差仿真分析

2.1 天线波束

仿真天线波束形状采用高斯型天线方向图(双向工作),表示为

(16)

式中θh是半功率波束宽度．

设高斯型天线方向图半功率波束宽度为2°,偏置角度θk为0.5°,则双天线波束、和差波束和误差信号响应分别如图1～3所示．

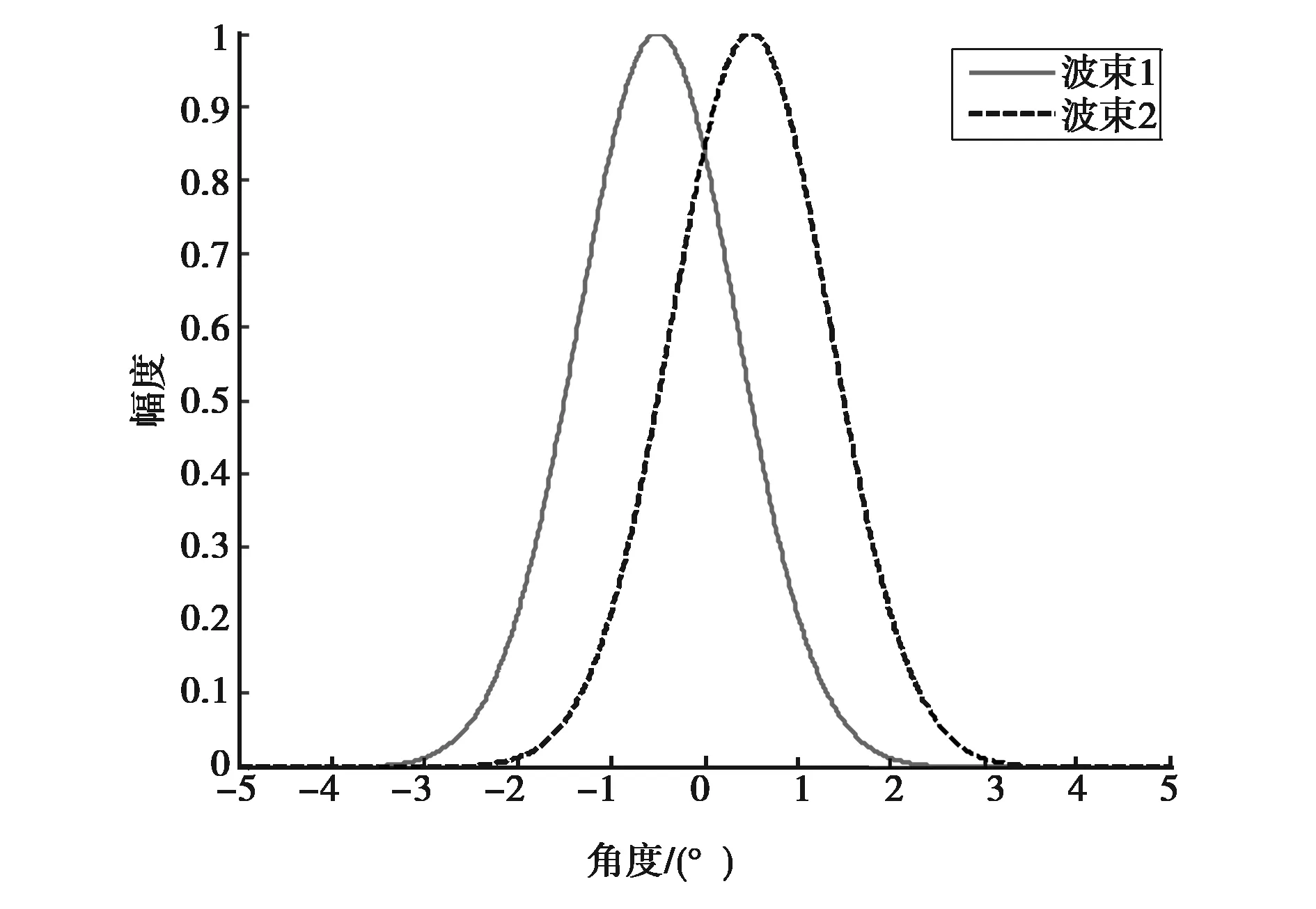
图1 双天线波束

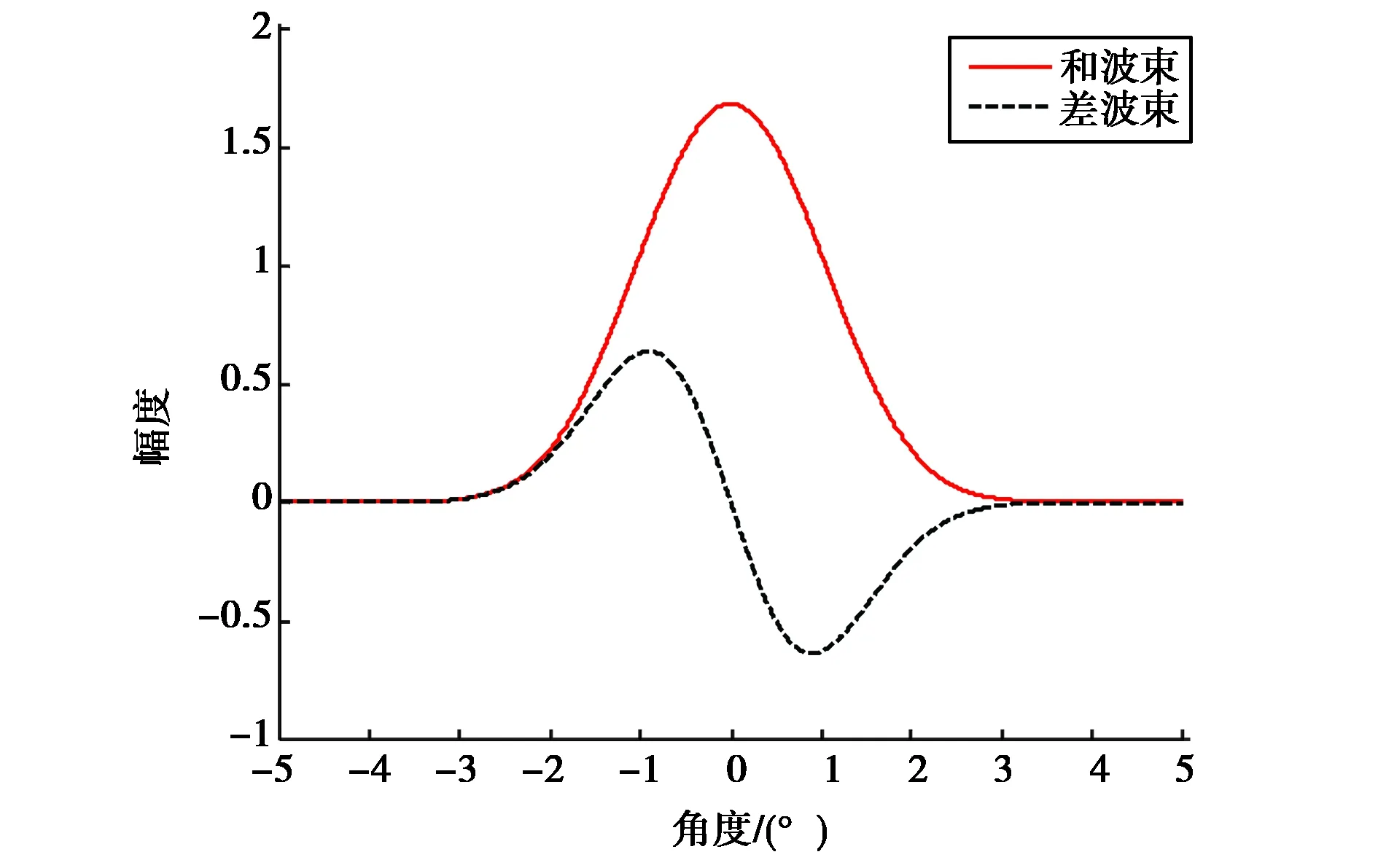
图2 和差波束

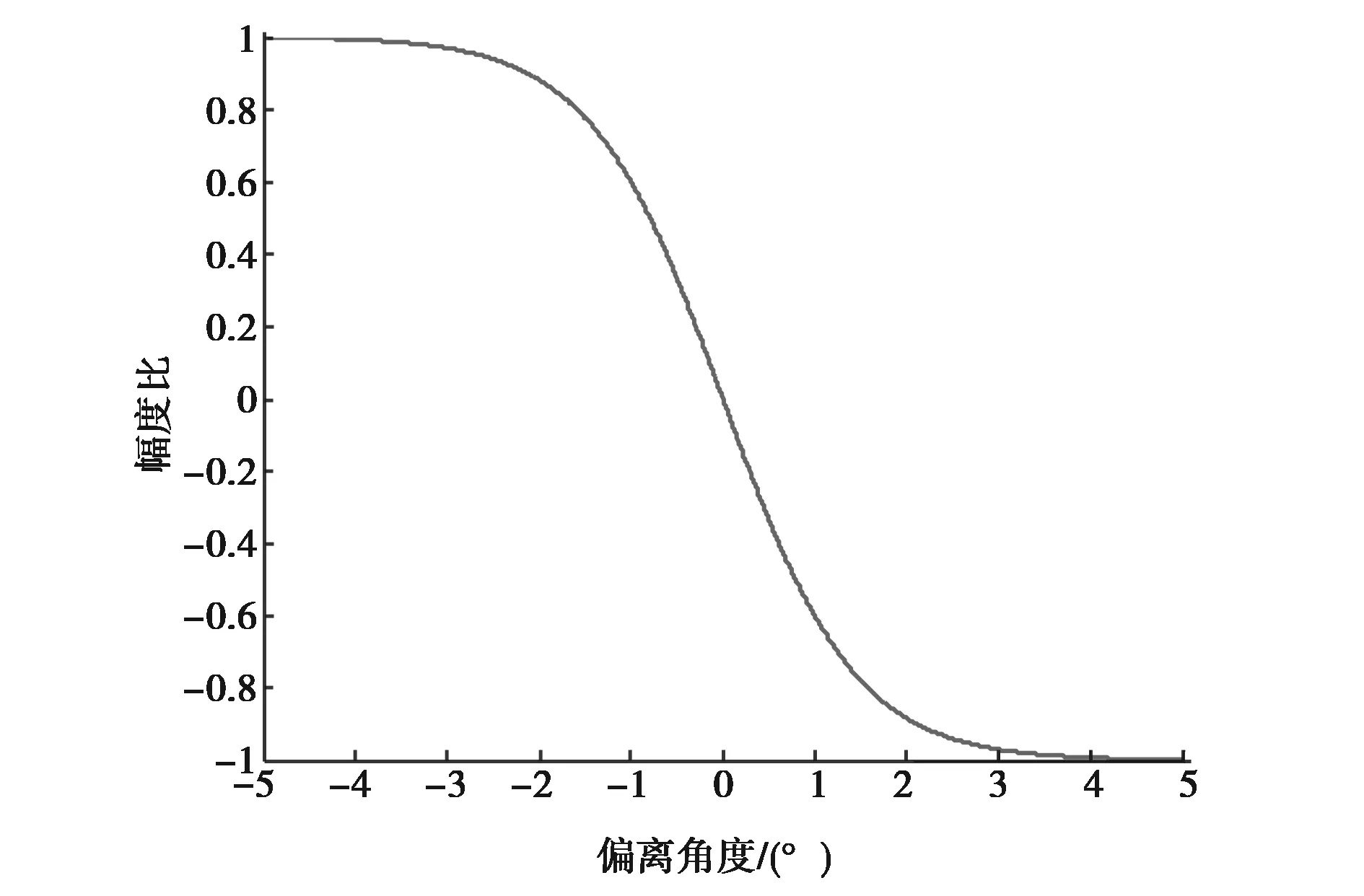
图3 误差信号响应

采用双波束测角具有以下优点:测角精度高,约为波束半功率宽度的2%,比最大信号法高约一个量级; 根据两个波束收到信号的强弱可判别目标偏离等信号轴的方向,便于自动测角．

2.2 方法检验

正常大气条件下,采用射线追踪的方法可仿真计算低仰角误差[2]．这里通过仿真S波段雷达低仰角跟踪误差结果,与基于射线追踪方法相比,验证本文所提方法的有效性．仿真频率3GHz,雷达天线高度20m,波束宽度为2.7°,偏置角度θk为0.5°,飞机目标在1 000 m高度上等高飞行．开始跟踪时目标地面距离为15 km,跟踪结束时目标地面距离为80 km,传播环境为标准大气折射环境和光滑海面,基于PE模型和射线(Ray Optics, RO)模型的目标仰角误差如图4所示．两者结果一致,表明基于PE方法的有效性．

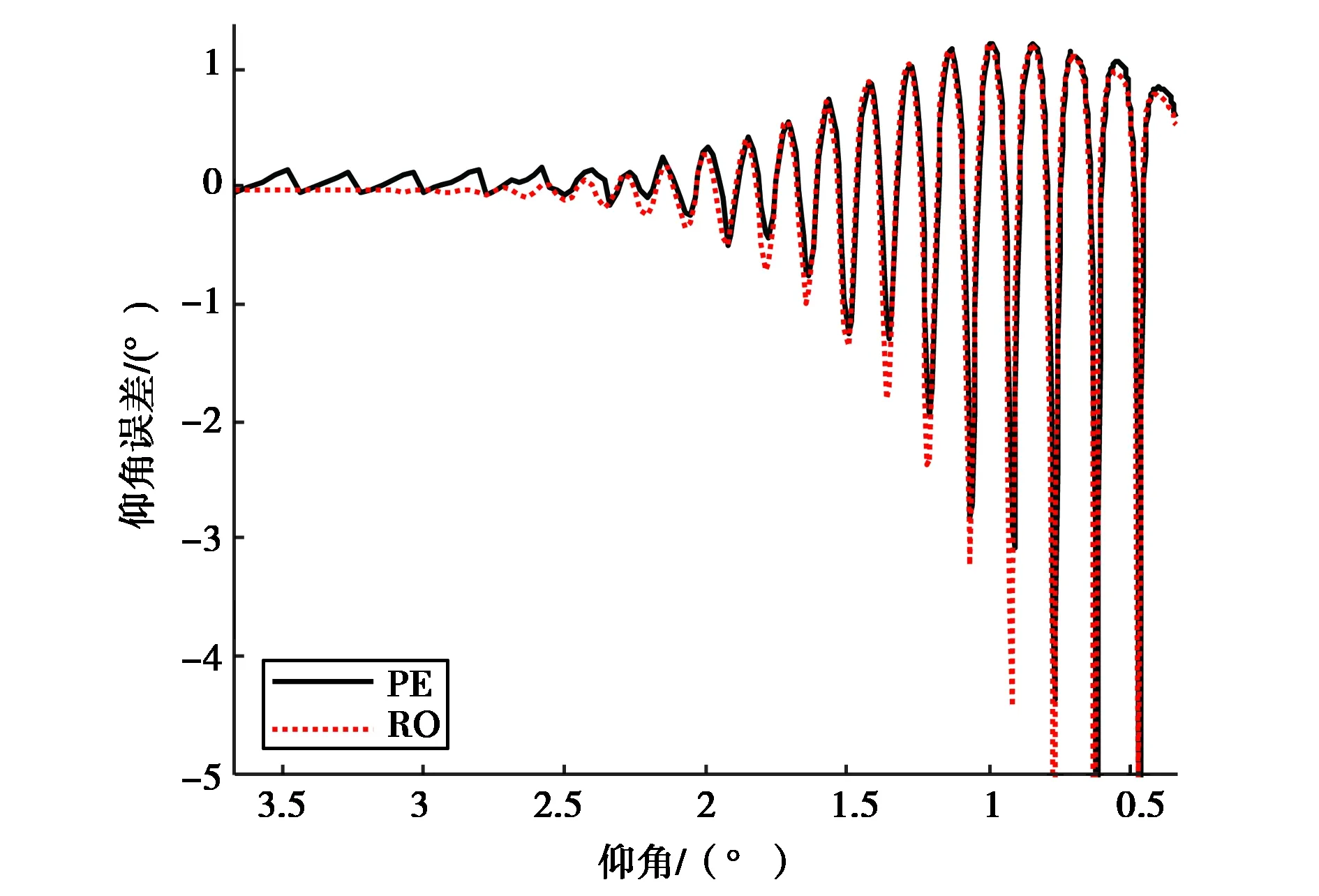
图4 基于PE模型和双射线模型的仰角误差对比

除正常大气和光滑海面的传播环境外,利用功能强大的电磁波传播的PE方法,可以计算更多实际复杂环境条件下的仰角误差．以下仿真计算中,均采用基于PE方法的模型．

2.3 仿真分析

首先给出光滑和粗糙海面(风速10 m/s)情况下的仿真结果．其它参数同上,目标仰角误差如图5所示．粗糙海面情况下,由于反射系数幅度相对变小,仰角误差随之变小,图5中结果反映了这种变化．

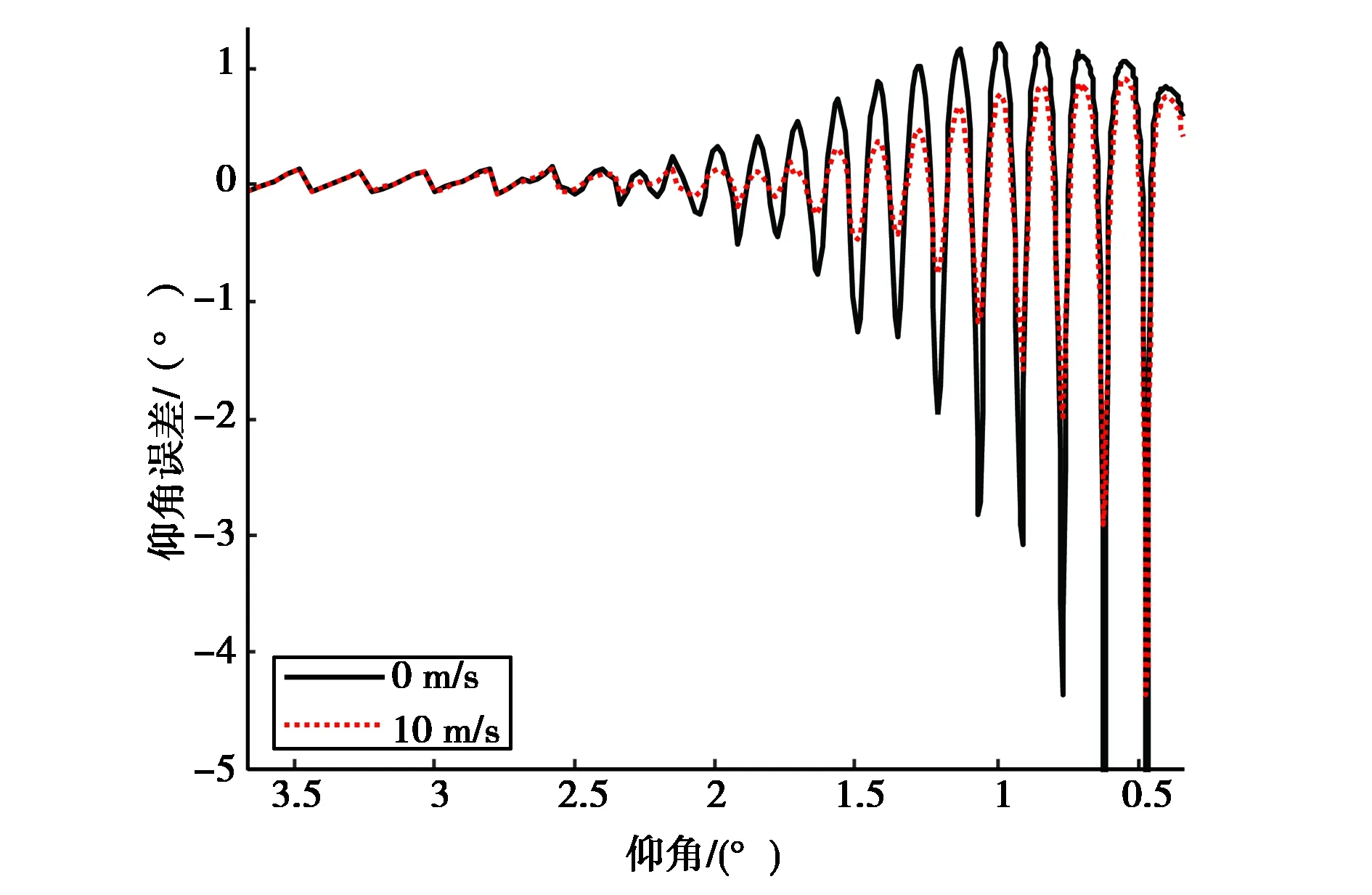
图5 不同粗糙面目标仰角误差

与射线方法相比,PE方法能够模拟多种实际环境下的电波传播效应．大气波导是一种复杂的大气折射环境,用PE方法可以计算出大气波导环境下的电波传播损耗或功率分布,而采用射线方法无法得到该结果．

仿真不同折射环境(表1)的目标仰角误差,如图6所示,海面为粗糙海面(风速10 m/s),其它参数同上．

改变目标高度为500 m,超折射和大气波导条件下,仰角误差如图7所示．

从图6和图7可以看出,低仰角情况下,虽然传播环境造成的误差中多路径误差是主要的, 但大气折射的变化显著影响着最终的误差,造成比单纯大气折射或单纯的多路径更大的影响．

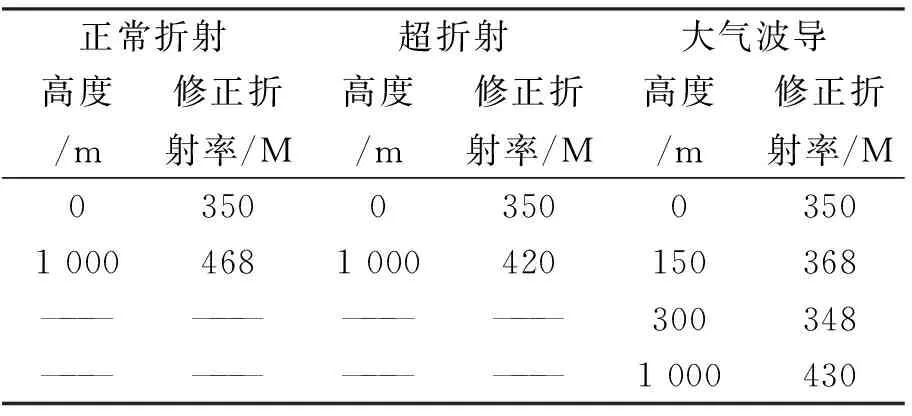
表1 折射环境

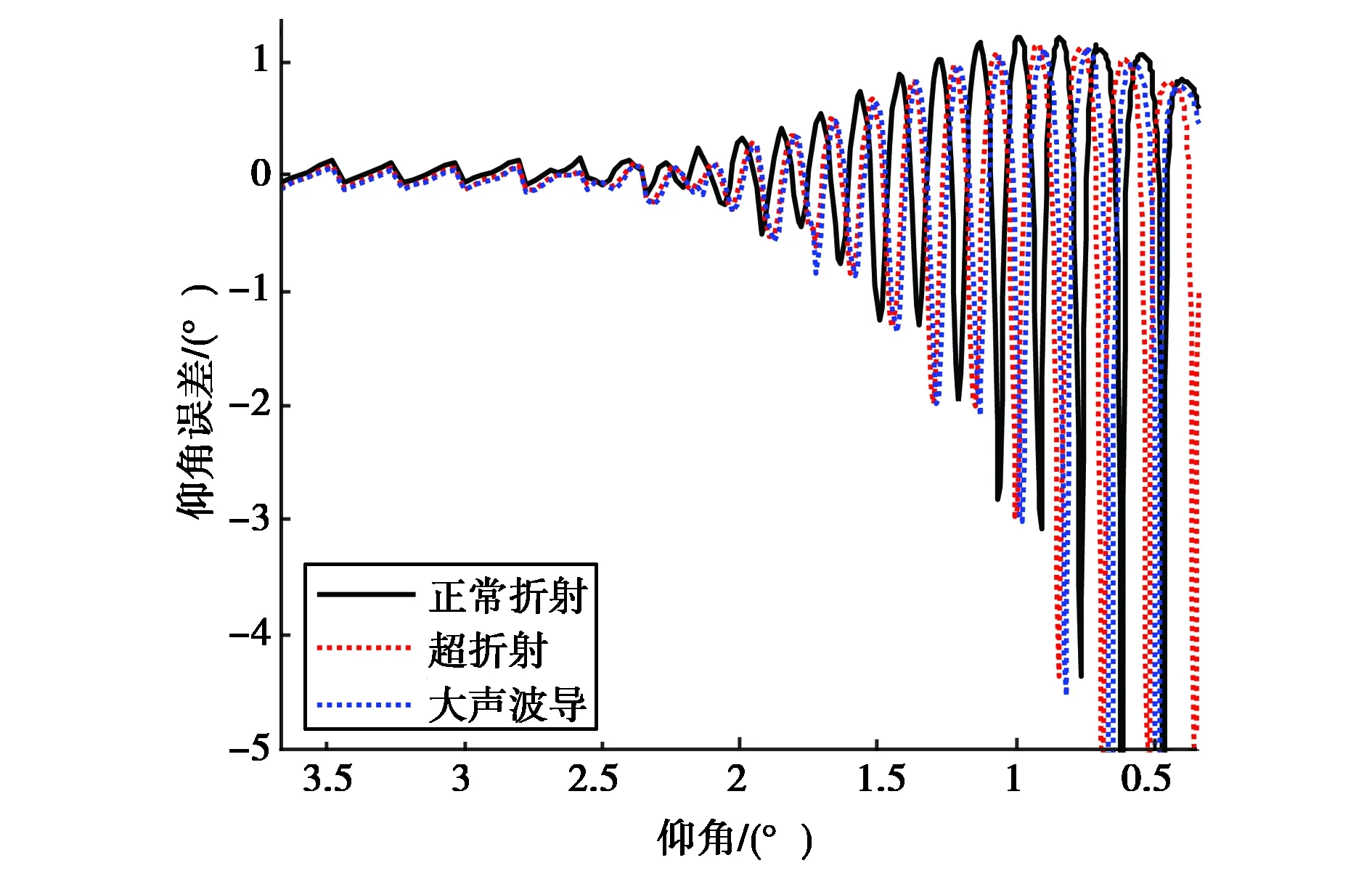
图6 不同折射环境目标仰角误差

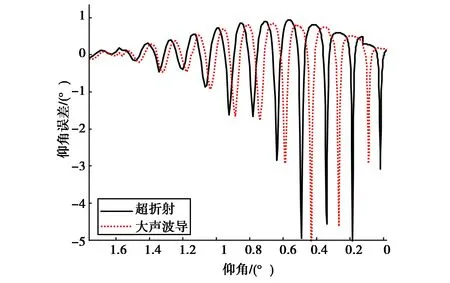
图7 超折射和大气波导情况仰角误差

基于PE方法,还可以很方便地仿真计算一些减少多路径误差措施的效果,如采用窄波束宽度和偏轴跟踪的方式．仿真频率3 GHz,雷达天线高度20 m,波束宽度分别为2.7°和1°,偏置角度θk分别为0.5°和0.3°,飞机目标在1 000 m高度上等高飞行．开始跟踪时目标地面距离为25 km,跟踪结束时目标地面距离为100 km,标准大气折射环境,粗糙海面(风速10 m/s)．结果如图8所示,波束宽度为1°时的最大误差绝对值约为2°,明显小于波束宽度为2.7°时约为5°的最大误差绝对值．

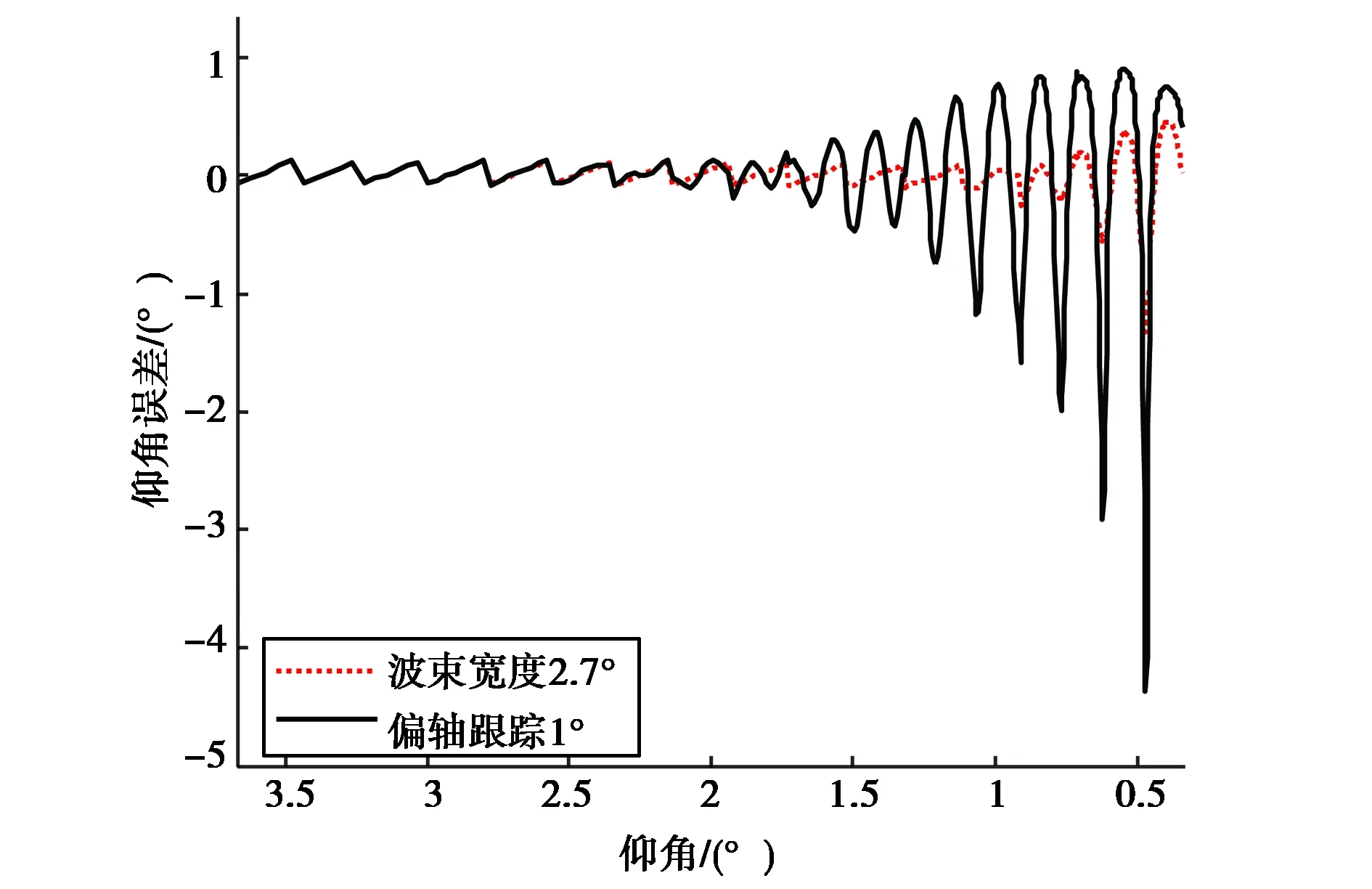
图8 窄波束跟踪仰角误差

采用偏轴跟踪时,天线指向锁定在正仰角0.7到0.8个波束宽度,跟踪精度只稍有提高,但往往可避免天线的大幅摇摆和跟踪丢失．设置天线视轴最小仰角为2°．偏轴跟踪模式仰角误差如图9所示．

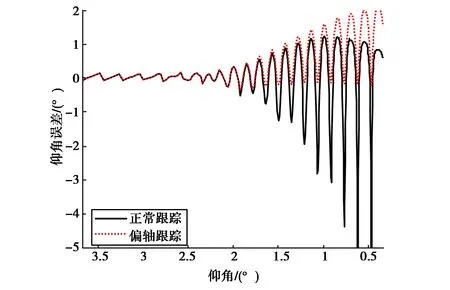
图9 偏轴跟踪仰角误差

3 结 论

本文针对雷达跟踪低空目标时传播环境造成的仰角误差问题,提出采用电磁波传播的PE方法进行仿真计算．低仰角误差主要是由多路径引起,仰角越低,误差往往越大．大气折射同样会引起仰角误差,也随目标仰角的降低而增大,并会改变多路径参数,从而引起比单纯大气折射更复杂、更大的影响．PE方法可模拟电磁波传播过程中的反射、折射、绕射等传播效应,本文基于该方法实现雷达跟踪低空目标仰角误差的仿真方法．实际雷达跟踪低仰角误差与雷达频率、天线方向图、工作方式、大气折射环境、海面粗糙度、目标位置等因素有关,PE模型可方便地综合考虑这些因素．本文结果表明,基于PE形成的方法能够预测复杂电波环境下的低仰角跟踪误差,实际大气环境可来自于气象探空、数值天气预报等．PE方法还可有效模拟复杂地形地物条件的电波传播问题,因此,当海面存在礁石、岛屿的场景下,同样可采用本文方法计算雷达仰角误差情况,预计将得到更为复杂的仰角误差结果．所提方法可用于试验数据分析、低仰角误差修正等．

[1] MENG Y S, LEE Y H. Measurements and characterizations of air-to-ground channel over sea-surface at C band with low airborne altitudes[J]. IEEE transactions on vehicular technology, 2011, 60(4):1943-1948.

[2] 王红光, 吴振森, 朱庆林. 大气折射对雷达低仰角跟踪误差的影响分析[J]. 电子与信息学报, 2012, 34(8):1893-1896.

WANG H G, WU Z S, ZHU Q L. Influence analysis of atmospheric refraction on low-angle radar tracking errors[J]. Journal of electronics & information technology, 2012, 34(8):1893-1896. (in Chinese)

[3] BOSSE E, DION D, FORTIN M. R, et al. Maximum likelihood beamforming in the presence of multipath and refraction effects[J]. IEE proceedings on radar sonar & navigation, 1994, 141(5): 263-269.

[4] BOMAN K, STOICA P. Low angle estimation: models, methods, and bounds[J]. Digital signal processing, 2001, 11(1): 35-79.

[5] KUTTLER J R, DOCKEY G D. Theoretical description of parabolic approximation/Fourier split-step method of representing electromagnetic propagation in the troposphere[J]. Radio science, 1991, 26 (2): 381-393.

[6] BARRIOS A E. A terrain parabolic equation model for propagation in the troposhere[J]. IEEe transactions on antennas and propagation, 1994, 42(1): 90-98.

[7] WANG H G, LIN F J, DONG X, et al. Influence of atmospheric duct on low-angle radar tracking errors[C]//11th International Symposium on Antennas, Propagation and EM Theory (ISAPE), October18-21, 2016, Guilin.

[8] SKOLNIK M I. Inroduction to radar systems[M]. McGraw-Hill Companies, Inc. 2001:210-246.

[9] DOCKEY G D, KUTTLER J R. An improved impedance-boundary algorithm for Fourier split-step solutions of the parabolic wave equation[J]. IEEE transactions on antennas and propagation, 1996, 44(12): 1592-1599.

[10] DING W W, WANG K, LONG Y L. Study of the electromagnetic waves propagation over the improved fractal sea surface based on parabolic equation method[J/OL]. International Journal of Antennas and Propagation, 2016: 8235752. [2016-11-13] http://dx.doi.org/10.1155/2016/8235752, October 2016.

[11] 王昆, 杨永钦, 龙云亮. 多刃峰环境无线电波传播预测的双向抛物方程法[J]. 电波科学学报, 2011, 26(6): 1058-1064.

WANG K, YANG Y Q, LONG Y L. Two-way parabolic equation approach for modeling radio wave propagation in the presence of multiple knife edges[J]. Chinese journal of radio science, 2011, 26(6): 1058-1064. (in Chinese)

[12] WANG K, LONG Y L. Propagation modelling over irregular terrain by the improved two-way parabolic equation method[J]. IEEE transactions on antennas and propagation, 2012, 60(9): 4467-4471.

曹淑艳 (1968-),女,黑龙江人,高工,硕士,研究方向为无线电外测事后数据处理,测控设备精度分析与评估．

王红光 (1980-),男,河南人,中国电波传播研究所高工,博士,研究方向为大气波导等电波环境与电波传播,及其在无线电系统中的应用．

董翔 (1987-),男,宁夏人,中国电波传播研究所工程师,硕士,研究方向为大气折射修正、大气波导、GNSS应用等．

The study of calculation method for radar tracking low altitude marine target

CAO Shuyan1WANG Hongguang2DONG Xiang2

(1.PLAUnit92941,Huludao125000,China; 2.ChinaResearchInstituteofRadiowavePropagation,Qingdao266107,China)

The problem of elevation errors due to propagation environment for radar tracking low altitude target is studied. Based on parabolic equation method for electromagnetic wave propagation, a new method for calculating low elevation errors is proposed, which can consider the effects of multipath and atmospheric refraction simultaneously. Validity of the proposed method is indicated by comparing with result from ray method under condition of standard refraction. Errors of elevation angle are simulated in different propagation environments, including rough sea surface and ducting environments. Variety of elevation errors after using narrow angle or bias axis tracking to decrease the effects of multipath are also simulated. The calculation process and simulation results show the comprehensive influence of complex environment involves multipath and ducting can be considered by the proposed method simultaneously, as well as other factors including radar parameters and working mode.

atmospheric duct; multipath; parabolic equation; low-angle tracking

10.13443/j.cjors.2016051902

2016-05-19

TN011.3;P412.25

A

1005-0388(2016)06-1153-06

曹淑艳, 王红光, 董翔. 雷达跟踪海上低空目标仰角误差计算方法研究 [J]. 电波科学学报,2016,31(6):1153-1158.

CAO S Y, WANG H G, DONG X. The study of calculation method for radar tracking low altitude marine target [J]. Chinese journal of radio science,2016,31(6):1153-1158.(in Chinese). DOI: 10.13443/j.cjors.2016051902

联系人： 曹淑艳 E-mail:caoshuyan_ch@163.com

DOI 10.13443/j.cjors.2016051902