基于复合网格方法的低频近场通信天线等效电路参数分析

张莉 逯贵祯

(中国传媒大学通信工程系,北京100024)

基于复合网格方法的低频近场通信天线等效电路参数分析

张莉 逯贵祯

(中国传媒大学通信工程系,北京100024)

为解决计算区域的大尺度与天线尺寸的小尺度问题,将复合网格法应用于近场通信(Near-Field Communication, NFC)天线等效电路参数的提取与计算,该方法可以在计算效率和计算精度之间达到很好的平衡．为避免麦克斯韦方程的“低频崩溃”问题,低频位移电流很小时,采用静态场方法分析低频NFC天线的近场参数．其中对线圈天线分布电容的计算不同于以往的实验测量、理论估算和数值计算等研究方法,而是基于其定义计算线圈相对于接地点的电容,该方法可以得到与参考文献一致的计算结果,同时具有能够分析周围环境对分布电容影响的优点．通过有限元分析，将复合网格法与均匀网格法的计算结果对比,证明了复合网格法在三维电磁场应用的可能性以及准确性．

复合网格;NFC天线;等效电路;有限元

引 言

随着无线通信的迅猛发展,与电磁近场相关的工程应用日益增多，其中近场通信(Near Field Communication, NFC)天线是在射频识别(Radio Frequency Identification, RFID)基础上发展起来的一种近距离无线通信技术,其通信频率为低频段13.56 MHz,近年来受到非常大的关注和研究[1-2]．

在NFC天线的静态场近似分析中,由于天线尺寸很小,通常是几毫米的大小,计算区域通常是天线尺寸的几十倍,因此带来很大的计算量．为了解决计算区域的大尺度与天线尺寸的小尺度问题,D. S.Wang[3]首次提出将复合网格法应用于电磁学领域,P.Ying[4]首次将复合网格法应用于分析运动电磁问题中运动体涡流区的计算,文献[5]讨论了复合网格法在稳态电磁学与运动电磁学中的应用，逯贵祯教授[6]首次将该方法应用于电小细线物体的二维电磁散射问题,但迄今为止未看到复合网格法应用于三维电磁场的问题求解．

NFC天线等效电路参数的提取方法大致可分为实验测量、理论估算以及数值计算方法三类:

1) 实验测量方法

Thomas Bauernfeind等通过阻抗分析仪获取1 MHz频率下的电阻和电感,利用谐振频率和关系式计算出13.56 MHz下RS、LS、CP的数值[7]．

该方法的优点是可以得到NFC天线的实际等效电路参数．但是对于与电路集成的NFC天线,其测量是一个非常复杂的过程．

2) 理论估算方法

文献[8]计算平面线圈电感数值时,基于Greenhouse的理论推导,分别计算每段平直线段的自感以及与其他线段的互感从而得到总的电感数值[8],该算法计算过程复杂,尤其对于多匝线圈．也有研究者提出环形和方形天线电感的数值可以通过文献[9]中公式估算,但公式中未考虑线圈的厚度,与实际值存在误差．

文献[10-12]均基于螺旋线圈计算其分布电容,其中文献[11]先算出两小段同心圆弧间电容,再通过螺旋线方程积分计算出总分布电容;文献[10]先计算基本结构单元的分布电容,再通过与邻近线圈的电容效应相互并联计算总分布电容．

该方法仅考虑邻近线圈之间的电容效应,对于平面螺旋线圈而言,不相邻线圈之间的电容效应也须加以考虑．

3) 数值计算方法

Thomas Bauernfeind[7]采用准静态磁场(Quasi-static magnetic field)、全波分析和HFSS软件计算NFC天线等效电路参数LS、RS和CP．文献中准静态分析方法由于忽略线圈的电容效应,只能计算出电阻和电感;全波分析法虽可以计算出三个等效数值,但耗费的内存和计算时间非常大．

考虑到麦克斯韦方程的“低频失效”,数值法在低频电磁场分析中,会遇到和波长相关的边界尺寸与天线精细结构的最小尺寸不能兼顾的限制．在计算近场参数时,低频位移电流的影响很小,因此本文提出将复合网格方法应用于三维电磁场问题中,利用静电场方法计算电容参数．电容的获取源自电容的定义式,计算线圈相对于接地点的电容．该思路不同于以往研究者们提出的电容方法,其优点在于根据接地点的位置计算线圈的分布电容,不仅可以计算自由空间线圈的分布电容,还可以计算由于环境因素所带来的分布电容变化．

本文在静电场条件下应用复合网格法计算分布电容,准确、省时且能减少求解的未知量数目,这将为电磁场低频段问题的求解提供非常重要的计算方法．

1 低频电磁场分析方法

1.1 低频电磁场的静态场近似

时变电磁场满足麦克斯韦方程

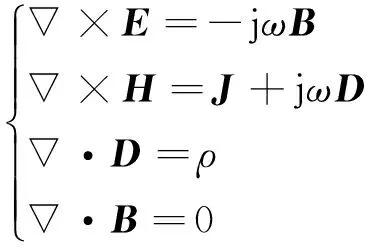
(1)

在频率很低时，磁场数值很小,所以式(1)中的第二式去掉jωD后对磁场影响很小．在电场的旋度方程中,电场的旋度与jωB有关,而该项与电场的散度分量相比也很小,可以近似忽略．因此,在低频近似条件下,只需求解磁场的旋度分量与电场的散度分量．对于电场的散度部分,由麦克斯韦方程可得静电势满足

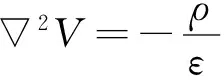
(2)

而电场与标势满足

(3)

对于磁场的旋度分量,由麦克斯韦方程可得矢势A满足

(4)

矢势A与磁通密度满足

B=×A.

(5)

1.2 复合网格计算方法

为了解决计算区域的大尺度与天线尺寸的小尺度问题,研究其整体性能,提高电磁数值计算的精度,传统的方法是重新对所有区域进行细小网格划分,这样的做法既增加了刚性矩阵的条件数,同时也带来计算量剧增、耗费大量计算机内存资源的问题,对于三维电磁散射问题尤其严重．复合网格法则利用区域分解法的思路,避免多重网格法在细密网格时需要在全局加密的缺点,根据想要得到精确解的位置对局部区域采用另一套网格并且进行加密处理．其中粗、细网格均为独立生成．

1.2.1 复合网格法原理

以二维平面分析为例说明复合网格法在计算图1(a)所示区域的应用．根据需要对图1(c)所示部分区域进行细网格的分析计算．利用复合网格法计算时,首先需要对整个区域进行粗网格分析, 如图1(b)

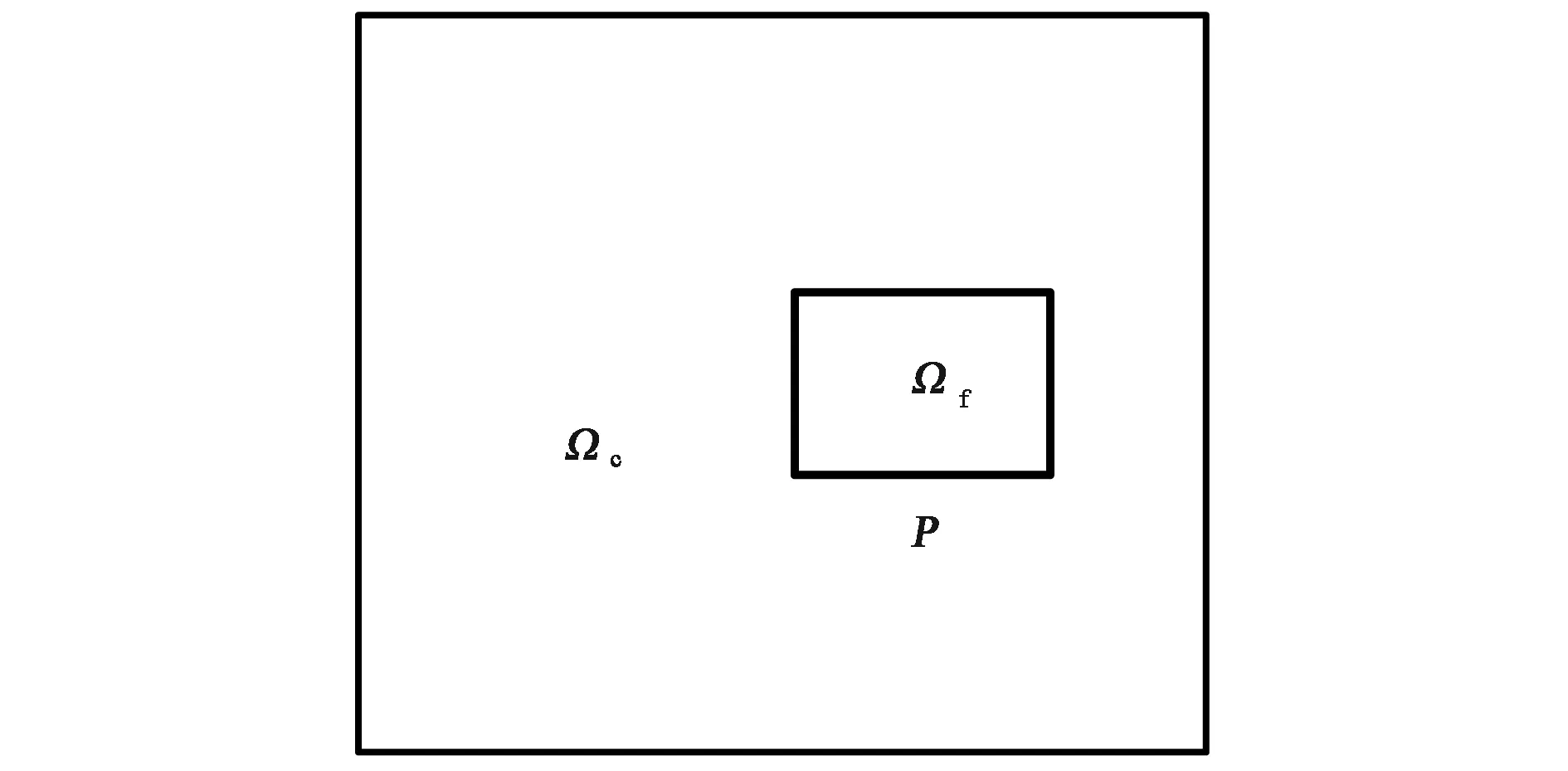
(a) 整体区域

(b) 粗网格计算区域

(c) 细网格计算区域图1 各种计算区域

所示，再利用粗网格的计算结果在粗细网格的交界处,通过插值方法给出细网格区域计算的边界条件,由此可实现大幅度减少未知量数目,同时又可以保证在所关心区域的计算精度．

考虑式(6)算子形式的偏微分方程求解问题:

Lu=f.

(6)

式中:L为偏微分算子;u为要求解的未知变量;f为源项．采用有限元方法分析低频NFC天线的近场特性时,对于粗网格区域,相应的算子方程和有限元伽辽金公式分别为:

Lcv=fc;

(7)

〈Lcu,δv〉=〈fc,δu〉.

(8)

式中:Lc为对应于粗网格的算子;v为对应粗网格方程(7)的解;fc为激励源函数．

对于细网格求解,细网格区域的边界采用粗网格计算的结果为细网格区域的边界,相应的算子方程和有限元伽辽金公式分别为:

Lfu=ff;

(9)

〈Lfu,δv〉=〈ff,δu〉

(10)

式中:Lf为对应细网格化分的算子;u是对应细网格方程(9)的解;ff是细网格的激励源函数．复合网格方法中,粗细网格可以独立划分,粗细网格之间通过边界条件连接．

(11)

v=VTDΦ．

(12)

式(7)和式(9)若改写为等效积分形式,计算表达式可改写为:

(13)

=VTD(〈LcΦT,Φ〉ΩfUc-〈fc,Φ〉Ωf)

-(〈LfΦT,Φ〉ΩfUf-〈ff,Φ〉Ωf)

=VTDK.

(14)

式中:系数K表示细网格计算值对粗网格的余量进行校正;D是粗网格计算值向细网格映射的插值矩阵,余量校正可以通过与D矩阵相乘作用到粗网格的计算方程中．细网格区域内部的任一点都满足式(7)和式(9),因此其对应的余量校正为零,而余量校正不为零的部分仅在细网格边界上．

在计算细网格问题时,粗细两个网格边界上的边界值可以通过式(15)的插值方法得到:

(15)

式中D矩阵的形式为

(16)

m为细网格的节点数;n为粗网格每个单元的节点数．

在细网格经过局域分析后,为得到更精确的电位和密度,局部区域的电位结果会再次应用于修正的全局分析,而修正的全局分析结果会再次反馈到局域分析中,这样经过多次的迭代计算,最终得到高精度的数值结果[13-14]．

1.2.2 复合网格法稳定性分析

在均匀网格方法中,要求网格单元之间是单值连续的,此时称单元之间是协调的．对于协调完备单元,有限元方法是稳定和收敛的．对于复合网格,粗网格与细网格之间是分别划分的网格,它们形成各自的有限元求解方程,粗细网格之间的联系通过插值方法实现,因此不会出现单元之间不协调所带来的不稳定问题．考虑如图2所示的粗细网格(以四边形网格为例说明)．

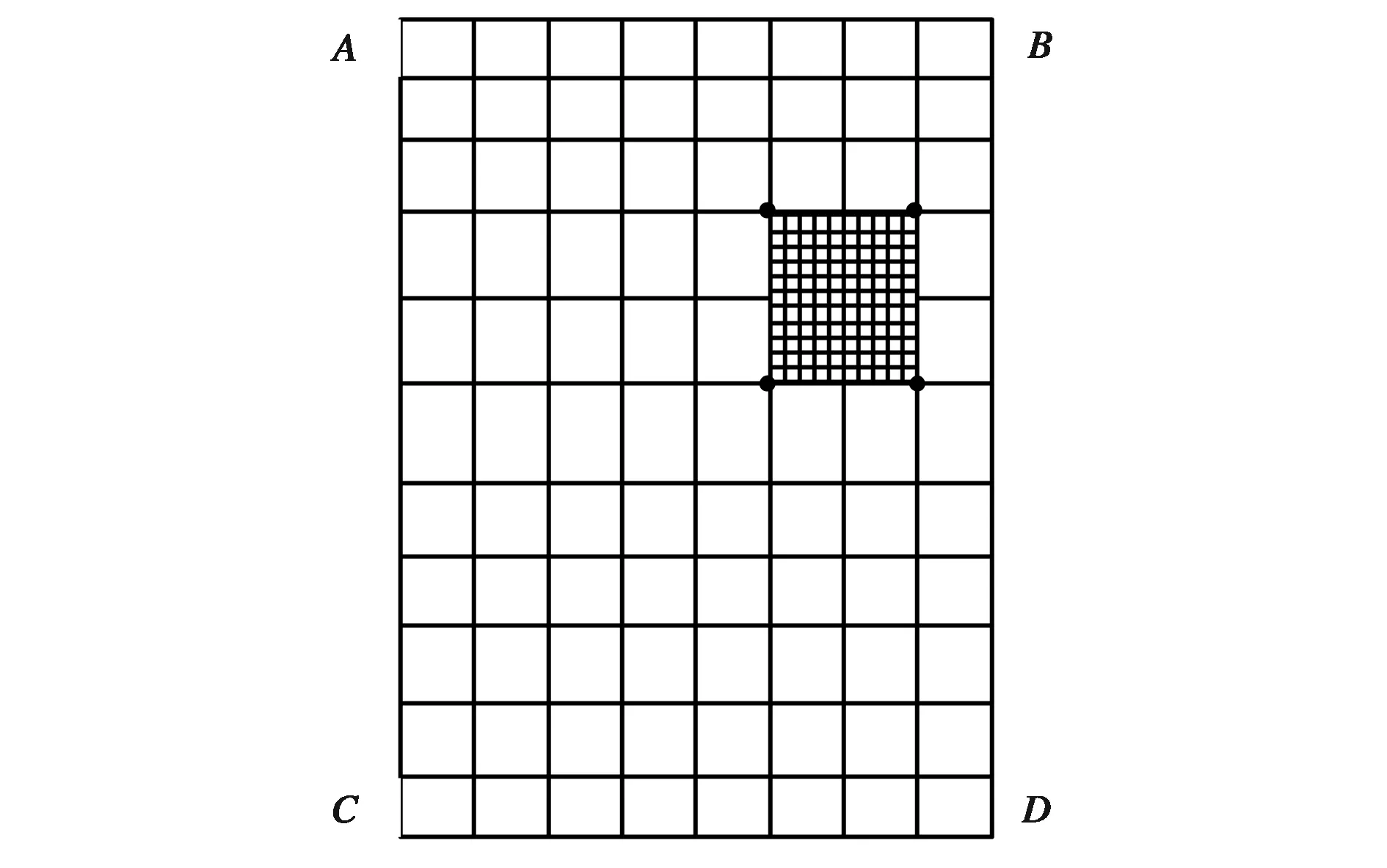
图2 粗网格的数值插值到细网格的边界

在细网格求解步骤中,利用ABCD所包围大四边形的粗网格得到的有限元数值解通过插值得到相应四个边上细网格位置上的节点值．这些数值确定后,求解细网格区域有限元解,这个过程不会出现连接边界函数值不协调的问题,因此是稳定和收敛的．在粗网格区域求解步骤中,中间细网格边界点的函数值作为粗网格的边界条件,同样也是稳定的边值问题,因此是稳定和收敛的．

2 低频NFC天线电磁场分析

一般NFC天线的螺旋线结构如图3所示,天线的输入阻抗计算对于实现天线与激励电路的匹配具有重要的影响,其等效电路如图4所示．

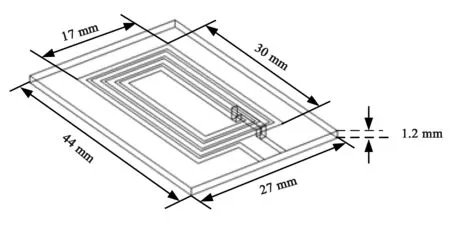
图3 带介质板的平面螺旋线圈模型

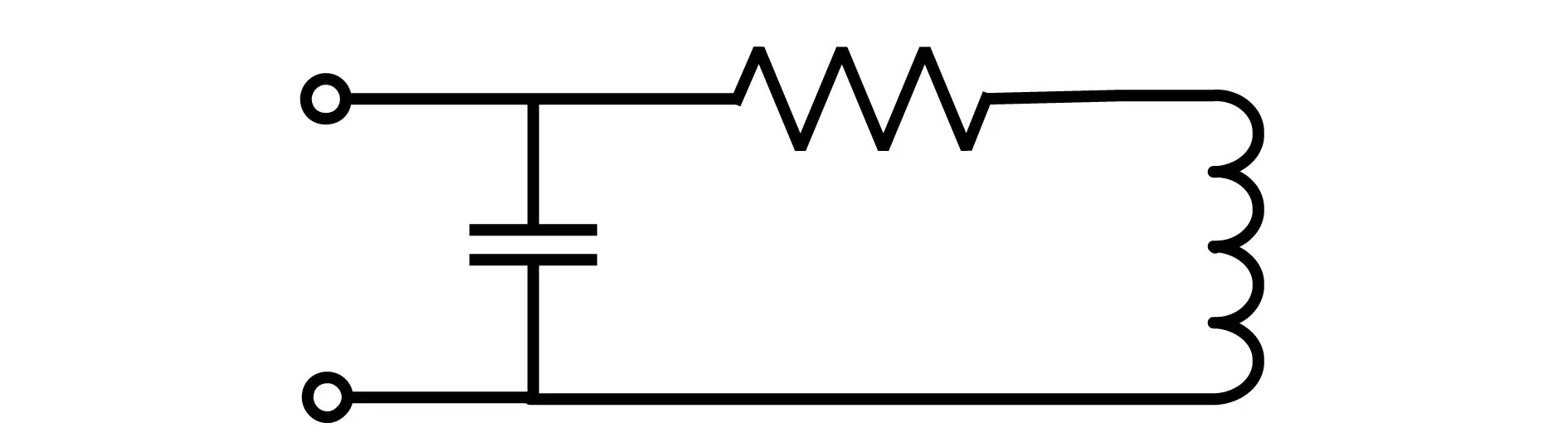
图4 螺旋线圈的等效电路

本文基于低频问题的准静态性质,提出利用静态场的方法提取NFC天线等效电路参数:利用静电场有限元方法计算电容．

在静态场的有限元计算中,可以采用无限元方法(Infinite Element Method, IFEM)截断无限大空间．无限元方法是处理无限大区域的一种网格剖分和相应基函数的方法,通过引入无限元网格和对应的基函数,可以非常逼近模拟无限计算空间．其边界设置如图5所示．

线圈天线分布电容的计算在目前文献的计算方法中,一种是利用射频方法计算线圈的谐振频率,再利用已经计算得到的电感,通过计算推导出分布电容．文献[7]提出了一种利用准静态场方法求解线圈分布电容的方法．在本文研究中,提出了另一种不同的求解线圈分布电容的方法,该方法根据电容的定义,直接计算线圈相对于接地点(零电位)的电容．这个方法的优点在于根据接地点的位置计算线圈的分布电容,不用去单独考虑线圈的内部电容,计算出来的结果即为自由空间中线圈的分布电容,另外还可以计算由于环境因素所带来的分布电容变化．

3 计算结果与讨论

为方便对比验证,我们选择与文献[7]相同尺寸的线圈:4匝矩形铜线圈,外围尺寸为30 mm×17 mm,线圈宽度为1 mm,间距为0.5 mm,厚度为35 μm,介质板材料为FR4,厚度为1.2 mm,如图3所示,并设定其无限元边界,如图6所示．

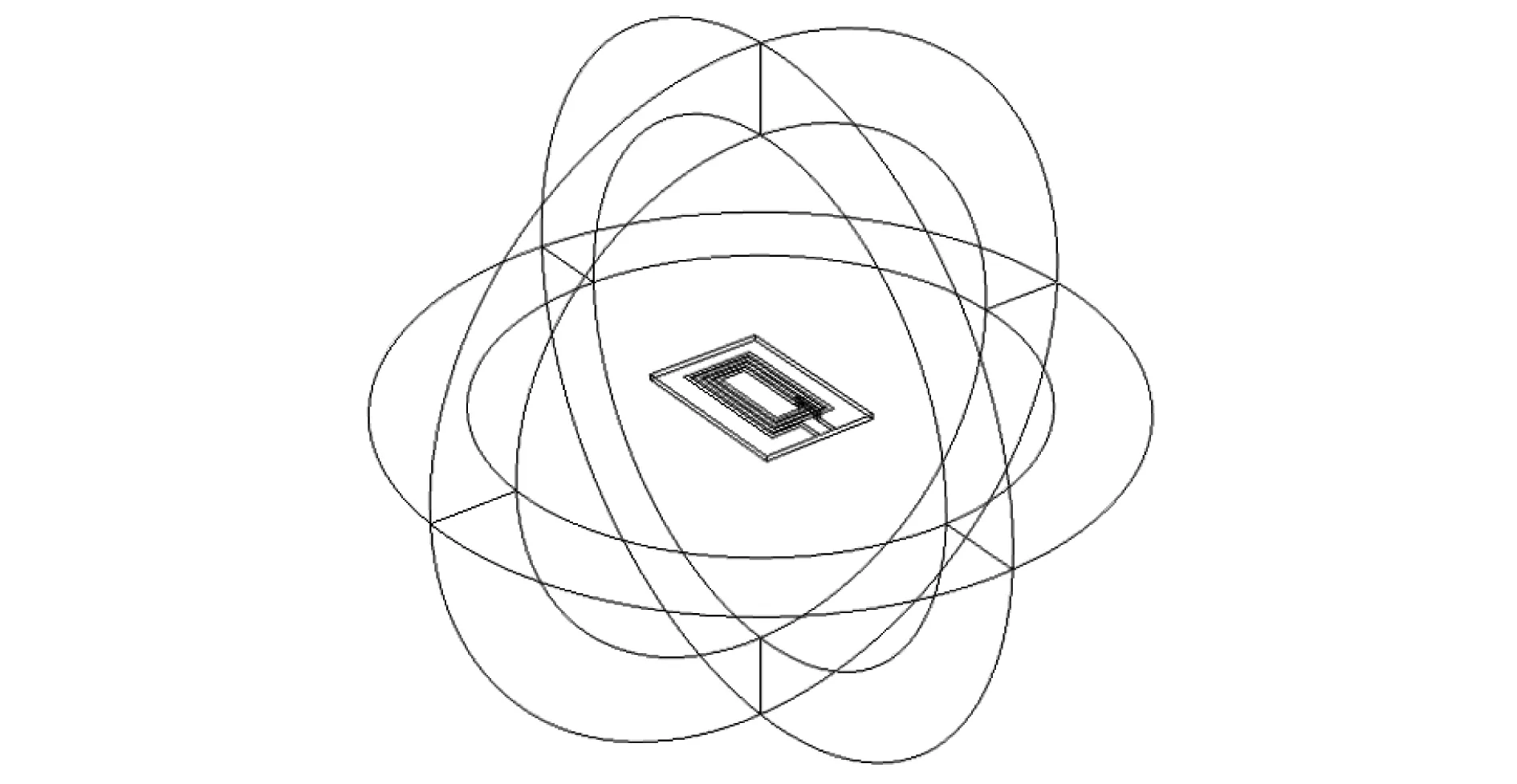
图6 无限元边界的线圈模型

利用复合网格法得到不同区域的粗网格与细网格,如图7所示．

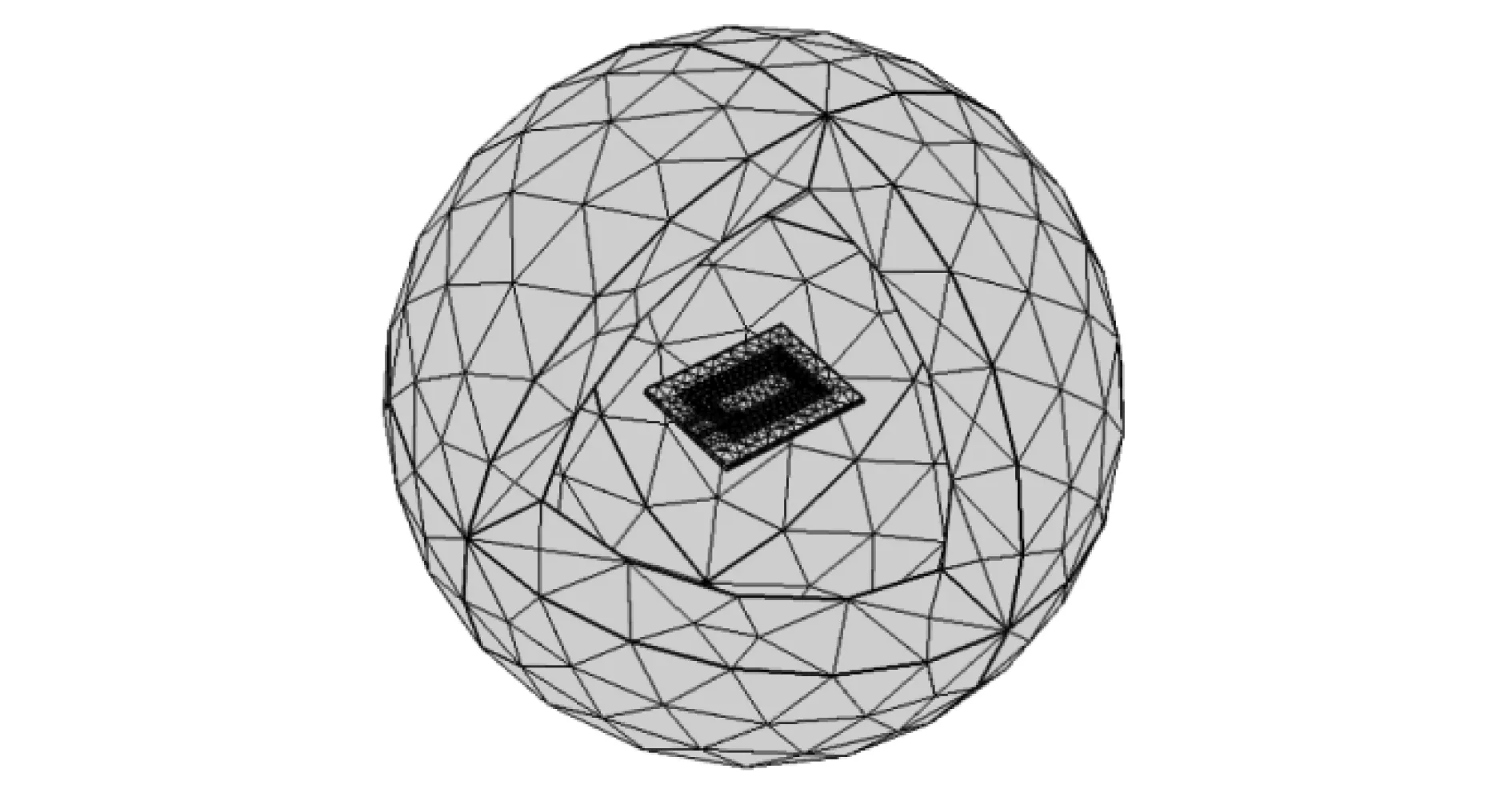
图7 不同网格尺寸划分

3.1 均匀网格法计算电容

在静电场作用下,用均匀网格法仿真计算出线圈电容数值,均匀网格剖分时,设置为精细网格,最小网格尺寸为2 mm,与文献[7]数据对比结果如表1所示．

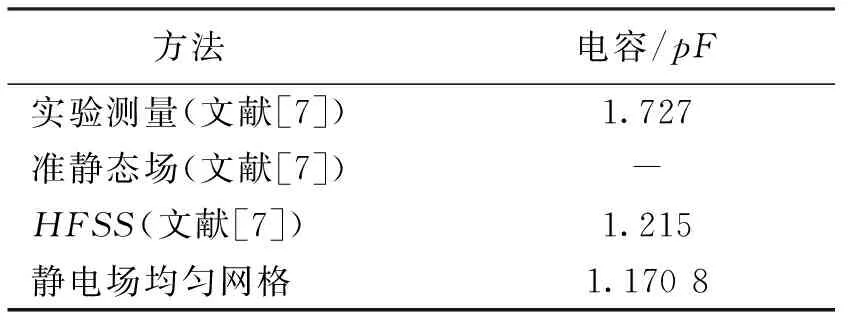
表1 电容数值结果对比

由表1可知,静电场均匀网格的数值结果与参考文献[7]的HFSS数据稍有差距,分析其原因:模型中线圈35 μm的厚度被忽略,由于35μm的厚度太薄,网格无法精细划分,会导致计算结果错误．基于电容数值与线圈厚度基本呈现正比关系,选择采用插值推算法,选择6种不同厚度线圈模型分别计算电感,结果如表2所示．

表2 不同线圈厚度的电容值

利用线性插值公式y2-y1=k(x2-x1)推算35 μm对应的电容数值,取其平均值,最后得到本文线圈模型对应的电容数值为1.199 9 pF．该结果与HFSS[7]计算结果1.215 pF非常接近,但二者与文献[7]的实验结果1.727 pF差距较大．分析其差距原因,可能为线圈的测试环境影响,若在线圈周围存在导体则导致地不在无限远,经对比发现随着地距离线圈越近,电容值越大,如图8所示,可看出线圈周围一旦出现导体,将直接影响其等效电容．

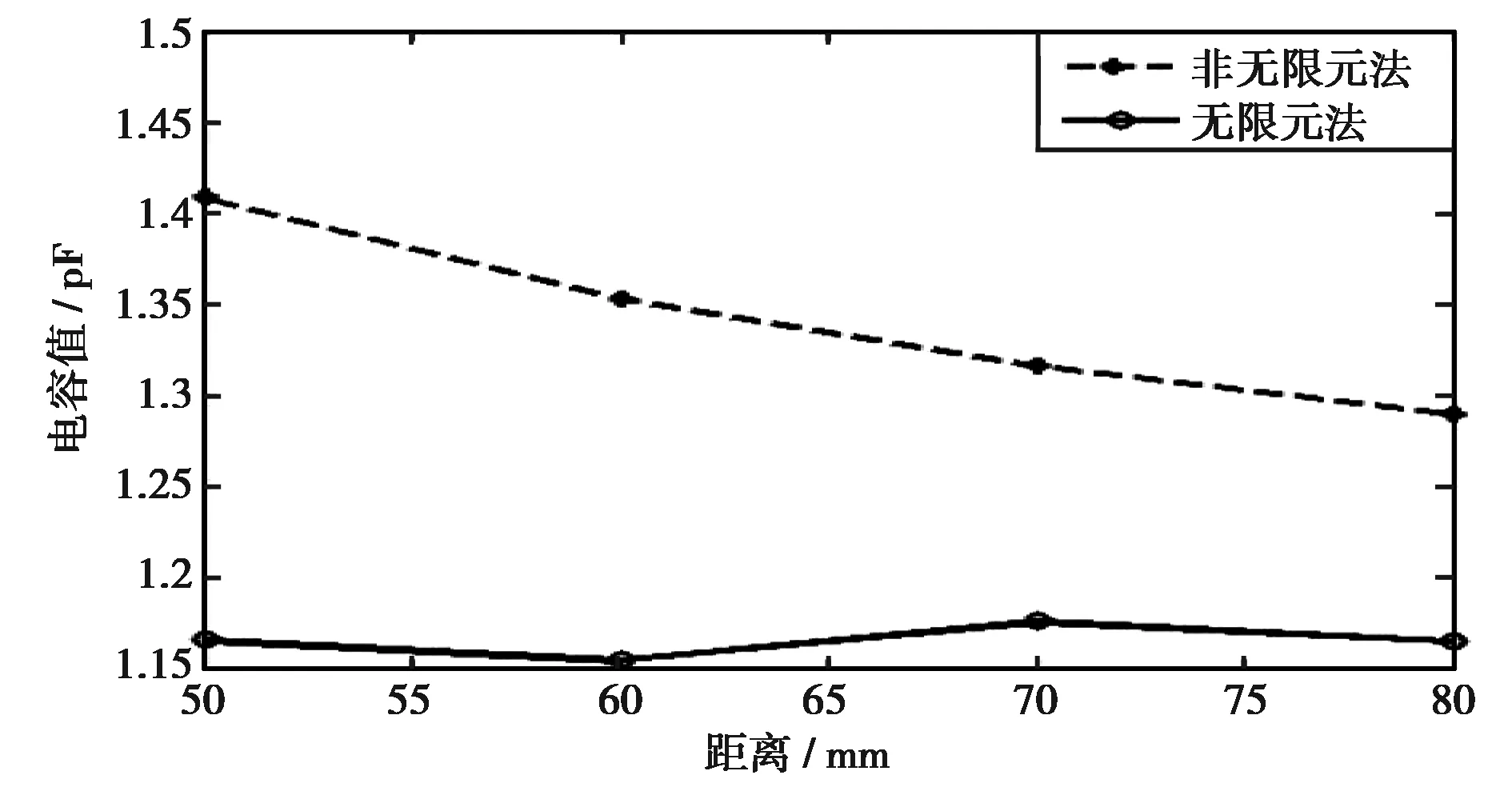
图8 非无限元法与无限元法的结果对比

3.2 复合网格法计算电容

以计算线圈分布电容为例,应用复合网格法剖分,在空气区域用粗网格(网格尺寸为3 mm,)剖分,在介质板和线圈区域用精细网格(网格尺寸为1 mm)．仍选择图6所示线圈模型,与均匀网格法对比数值结果,以及未知量数目和耗时,如表3所示．

表3 复合网格法与均匀网格法对比

表3中均匀网格法使用的计算机配置为:64位操作系统,处理器为Intel Xeon CPU E5-2660 @2.2 GHz(双处理器),内存128 G; 复合网格法使用的计算机配置为: 32位操作系统,IntelCore i7-2640M CPU@2 GHz,内存4 G．从数据结果可以看出,由于复合网格法利用迭代算法,其求解的未知量数目少于均匀网格法,即使计算机配置降低,内存减少,其求解时间依然比均匀网格法缩短约57%,并且相比于均匀网格划分,计算结果与实验结果(实验结果包含了周围环境对于线圈的影响,因此更接近真实等效数值)更加接近．如若为提高计算精度,进一步加密均匀网格,其未知量数目将大大增加,计算耗时大大增加,对计算机的配置要求依然很高,因此从计算耗时、计算机配置以及未知量求解数目和结果精度来看,复合网格法在三维电磁场应用的求解中,可以成为一个非常好的减少未知量、提高计算精度的方法．

3.3 相对误差对比分析

以文献[7]实验测试电容数值1.727 pF为基准,将几种方法得到的电容相对误差汇总,见表4．

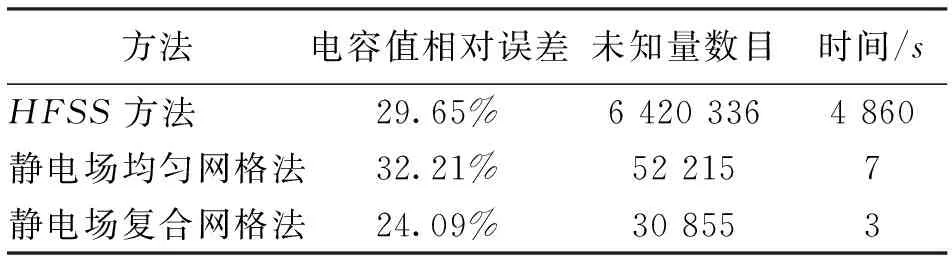
表4 相对误差对比

由表4可见静电场均匀网格法与HFSS方法的数值,相对于实验测试值的相对误差很接近,但其未知量和耗时相对HFSS方法却极大地减少,证明了应用静电场复合网格法计算分布电容方法,准确、省时且能减少求解的未知量数目,这将为电磁场低频段问题的求解提供非常重要的计算方法．

4 参数讨论

基于线圈分布电容的计算结果,我们继续深入讨论有限元仿真参数设置对数值求解结果的影响．选择网格尺寸大小、边界球半径大小以及无限元厚度三个参数进行讨论．

4.1 网格尺寸参数

有限元方法将求解域近似为具有不同有限大小和形状且彼此相连的有限个单元组成的离散域,习惯上称为有限元网络划分．显然单元越小(网络越细)则离散域的近似程度越好,计算结果也越精确,但计算量及误差都将增大,因此求解域的离散化是有限元法的核心技术之一．在本文模型中我们利用多尺度划分网格:介质板和球体采用粗网格,螺旋线圈部分采用精细网格,改变精细网格的尺寸,从5 mm变化到0.25 mm,分别计算电容数值．

我们发现网格划分越粗,电容数值越大,随着网格尺寸减小,电容值减小并逐渐趋于不变．由此可见网格的设置对于计算结果的影响不可忽略．

4.2 边界球半径参数

边界球的大小决定了截断空间的大小,我们设定半径大小从50 mm变化到1 000 mm,随着边界球半径的增大,电容值亦发生变化,边界设定越大,其仿真环境越逼近真实空间．但同时也会急剧增加未知量数目,需要在二者之间权衡．

4.3 无限元厚度参数

处理无界域时引入一种几何上无限大的“有限”单元,在概念上它是有限元的延伸,是一种在几何上可以趋于无限远处的单元,但由于无限元必须反映近场的边界特征或与模拟近场的有限元结合,它实际上只在一个方向趋于无限[15]．

无限元的厚度参数选择从5 mm变化到38 mm,随着无限元厚度增加,电容值变化幅度不大,说明该参数数值变化对于计算结果的影响可以忽略．

5 结 论

本文将复合网格法应用于NFC天线的等效电路参数的提取与计算,为避免麦克斯韦方程的“低频崩溃”问题,在提取NFC天线的电路等效参数时,创新性地利用静电场和静磁场有限元分析方法与无限元方法的结合,有效地截断无限远边界,模拟静态场中的无限大空间,计算出NFC天线线圈的分布电容．这与传统高频仿真软件的计算方法大不相同,同时也克服了高频仿真软件在解决低频问题时的困难．

通过复合网格法与均匀网格法的计算结果对比,证明了复合网格法在三维电磁场应用的可能性以及准确性;通过与文献[7]的HFSS仿真数据对比,静场分析法与其相对误差均低于1.3%,证明了静态场近似方法的正确性与可行性,这将为低频及以下频率的问题分析提供非常重要的计算手段,弥补了有限元法在低频段问题计算的不足．

鉴于线圈很薄,仿真模型的平面线圈并不能完全等同于实际模型,在数据处理中本文通过插值推算法得到更精确数值．

最后通过调整划分网格大小、边界球半径以及无限元厚度三个参数,讨论其对仿真数值结果的影响,其变化规律也将对有限元分析设定参数提供参考依据．

[1] 刘艳峰, 魏兵, 任新成. 近场通信天线场分布特性仿真[J]. 电子测量技术, 2015, 38(8):132-134.

LIU Y F, WEI B, REN X C. Near field communication antenna field distribution simulation[J]. Electronic measurement technology, 2015, 38(8):132-134. (in Chinese)

[2] 陈思远, 刘强, 李旺昌, 等. 无线充电和近场通信兼用贫铁MnZn铁氧体材料[J]. 电子测量技术, 2015, 34(5): 38-41.

CHEN S Y, LIU Q, LI W C, et al. MnZn ferrites with Fe-poor composition and its potential application in wireless charging and NFC[J]. Electronic component & device applications, 2015, 34(5): 38-41. (in Chinese)

[3] WANG D. Composite grid method for analysis of electromagnetic field[J]. Journal of Southeast University, 2003, 19(1): 49-52.

[4] PENG Y, RUAN J J, ZHANG Y, et al. A composite grid method for moving conductor eddy-current problem[J]. IEEE transactions on magnetics, 2007, 43(7):3259-3265.

[5] 甘艳, 阮江军, 张宇, 等. 组合网格法及其在电磁问题中的应用[J]. 电工技术学报, 2008, 23(11): 8-14.

GAN Y, RUAN J J, ZHANG Y, et al. Combined grid method and its application in electromagnetic problems [J]. Transactions of China electrotechnical society, 2008, 23(11):8-14. (in Chinese)

[6] 逯贵祯, 杨莉, 殷红成, 等. 复合网格法在电磁散射问题中的应用研究[J]. 电波科学学报, 2013, 28(1): 162-164.

LU G Z, YANG L, YIN H C, et al. Application of composite grid method in electromagnetic scattering[J]. Chinese journal of radio science, 2013, 28(1):162-164. (in Chinese)

[7] BAUERNFEIND T, RENHART W, SCHEMTHANNER S, et al. Equivalent circuit parameter extraction for controlled detuned NFC antenna systems utilizing thin ferrite foils [C]//12th International Conference on Telecommunications. IEEE, June 26-28, 2013:251-256.

[8] 杨卓, 董天临. 射频电路中平面螺旋电感的计算[J]. 电子元器件应用, 2007(1):57-60.

YANG Z, DONG T L. Calculation of inductance of the spiral coil in RF circuit[J]. Electronic component & device applications, 2007(1):57-60. (in Chinese)

[9] 戴彩艳, 蔡坚勇, 陈银燕, 等. 13.56MHz RFID读写器天线的设计与仿真[J]. 无线电工程, 2013, 43(1): 42-45.

DAI C Y, CAI J Y, CHEN Y Y, et al. Design and HFSS simulation of 13.56MHz RFID reader antenna[J]. Radio engineering, 2013, 43(1): 42-45. (in Chinese)

[10]郑羽, 李红志, 梁捷, 等. XCTD剖面仪螺旋电感固有电容的建模与分析[J]. 海洋技术, 2013, 32(1): 21-23.

ZHENG Y, LI H Z, LIANG J, et al. Capacitance simulation of XCTD spiral coils[J]. Ocean technology, 2013, 32(1): 21-23. (in Chinese)

[11]王昕, 王宗欣, 袁晓军. 圆形螺旋线圈的自感和分布电容的计算[J]. 固体电子学研究与进展, 2000, 20(4): 424-432.

WANG X, WANG Z X, YUAN X J. Calculation of self-inductance and distributed capacitance of spiral inductor [J]. Research & progress of SSE, 2000, 20(4): 424-432. (in Chinese)

[12]王莹莹, 高建森, 罗小彬, 等. 螺旋线圈的分布电容及其磁电容效应[J]. 应用物理, 2013, 3(2): 44-49.

WANG Y Y, GAO J S, LUO X B, et al. Distributed capacitance of spiral coils and its magneto-capacitance effect[J]. Applied physics, 2013, 3(2): 44-49. (in Chinese)

[13]SU T, LIU W, WANG Y, et al. A composite compensation method of a grid-connected AC/DC converter to improve robustness under weak grid conditions[C]//2015 IEEE Energy Conversion Congress and Exposition. IEEE, September 20-24, 2015: 6853-6857.

[14]KANG T, CHEN T, ZHANG H, et al. A-Φ finite element method with composite grids for time-dependent eddy current problem[J]. Applied mathematics & computation, 2015, 267(C): 365-381.

[15]李录贤, 国松直, 王爱琴. 无限元方法及其应用[J]. 力学进展, 2007, 37(2): 161-174.

LI L X, GUO S Z, WANG A Q. The infinite element method and its application[J]. Advances in mechanics, 2007, 37(2): 161-174. (in Chinese)

Equivalent circuit of the near field communication antenna at low frequency based on composite grid method

ZHANG Li LU Guizhen

(DepartmentofCommunicationEngineering,CommunicationUniversityofChina,Beijing100024,China)

To solve the conflict of the large scale and the small scale in the solution domains, the finite element composite grid method (CGM) is put forward in the equivalent circuit parameters extraction for the near-field communication(NFC) antenna. This method is to balance the calaulation efficiency and the accuracy. To avoid the breakdown of Maxwell equations at low frequency, the static field method is proposed for extracting the equivalent circuit parameters for the NFC antenna, considering the low value of the displacement current at low frequency. The distributed capacitance of the NFC antenna was usually got by the measurement method, the theoretical estimation method and the full wave analysis method before. Different from those methods, in this paper a novel method based on the definition of capacitance, is obtained by computing the capacitance of the coils relative to the ground. The results are coincident with the references, meanwhile, this method can also estimate the effects of the surroundings. Additionally, the comparison of the regular finite element method and the composite grid proves the practicability in electromagnetic 3-D model.

composite grid method; NFC antenna; equivalent circuit; finite element

10.13443/j.cjors.2016032101

2016-03-21

TN820

A

1005-0388(2016)06-1145-08

张莉 (1978-),女,山西人,硕士,副教授,主要从事计算电磁数值仿真、电磁兼容方面的研究．

逯贵祯 (1957-),男,北京人,博士,教授,主要从事天线设计、电磁计算和电磁兼容方面的研究．

张莉,逯贵祯.基于复合网格方法的低频近场通信天线等效电路参数分析[J]. 电波科学学报,2016,31(6):1145-1152.

ZHANG L, LU G Z. Equivalent circuit of the near field communication antenna at low frequency based on composite grid method[J]. Chinese journal of radio science,2016,31(6):1145-1152. (in Chinese). DOI: 10.13443/j.cjors.2016032101

联系人： 张莉 E-mail: zhangli@cuc.edu.cn

DOI 10.13443/j.cjors.2016032101