电极移动速度效应的空气动力学分析

周奎 阮方鸣 张景 苏明 王珩

(1.贵州大学大数据与信息工程学院,贵阳 550025;2.北京东方计量测试研究所，北京 100094；3.贵州师范大学大数据与计算机科学学院,贵阳 550001;4.复旦大学 电磁波信息科学教育部重点实验室,上海 200433)

电极移动速度效应的空气动力学分析

周奎1,2阮方鸣2,3张景4苏明3王珩3

(1.贵州大学大数据与信息工程学院,贵阳 550025;2.北京东方计量测试研究所，北京 100094；3.贵州师范大学大数据与计算机科学学院,贵阳 550001;4.复旦大学 电磁波信息科学教育部重点实验室,上海 200433)

基于空气动力学原理解释了电极向靶运动过程中放电间隙形成局部低真空的机理．结合小间隙放电的双过程模型,初步阐释了气体压强变化对放电间隙内部相关电参量的影响机理,进而分析电极速度对放电参数的影响．基于我们团队自主研制的电极移动速度效应检测仪，进行反复实验,对大量的试验数据进行仿真分析,探索小间隙静电放电过程中放电参数对电极移动速度的依赖性．结果表明:电极移动速度与放电电流峰值、放电电流脉冲上升速度,具有高度的正相关性;与放电电流脉冲下降速度具有高度的负相关性．研究结果对于推进非接触静电放电测试标准的提出具有一定的参考意义．

静电放电;电极移动速度;气体压强;相关性

引 言

静电危害防护和静电放电测试,是工业、国防、航空航天、军事武器以及民用电子电器产品等领域极为关注的问题．瑞士联邦理工大学B Daout, HRyser和A Germond 于20世纪80年代提出了带电体向受电体快速移动的速度对放电参数产生明显影响的问题[1]．美国密苏里科技大学的D Pommerenke、 M Aidam等,对静电放电的电极移动速度效应进行了一些研究[2-3]．电磁环境效应国家重点实验室研究团队,用步进电机驱动静电放电枪的实验装置,就气体压强、电极接近速度等因素影响空气放电结果的现象进行了分析讨论[4]．在电磁兼容静电放电研究领域,如何尽量提高电极向靶移动速度，同时又要避免强烈碰撞造成设备损坏,一直困扰各国的研究者们．经过多年艰苦努力,我们电磁兼容团队成功研制发明了电极移动速度效应检测仪．该新型静电放电测试系统利用曲轴连杆原理,将电机摆臂的圆周运动转化为放电枪的直线运动,解决了长期困扰研究者们的这一难题．使用该新型测试仪器,我们在静电放电研究中取得了明显的进展和有益的成果[5-9]．

电极以不同速度向靶移动放电,放电参数具有明显的离散性和低重复性[10-11],在研究过程中,采集了大量的实验数据和放电波形,并用Matlab软件对提取的实验数据进行拟合仿真,最后采用实验验证相结合的方式进行了探讨分析．基于空气动力学原理,解释了电极快速向靶移动形成局部低真空的机理;根据帕邢定律描述了气体压强对静电放电相关电参量影响的物理过程;结合S Bonisch等提出的电子雪崩过程和表面发射过程放电模型[12],从理论和实验上对电极速度与静电放电参数的依赖关系进行深入讨论．

1 实验装置及测试方法

电极移动速度效应检测仪是我们电磁兼容团队研制的用于静电放电参数测试的仪器,主要用于对电气与电子设备产生的静电放电电流等参数进行测试,已获得国家发明专利授权(专利号:ZL201320024841.7)．它主要由密闭箱体,曲轴连杆,电动机,控制器和静电放电发生器等组成．在密闭箱体内的侧壁上安装有放电靶,电动机用电机支架固定在箱体中,电动机与放电靶间的导轨上安装有放电枪,放电枪用曲轴连杆与电动机的输出轴连接．此外,密闭箱上还设置有能与真空泵相连接的管路,可以连接真空泵来调节密闭箱内的气压,负压表用于对密闭箱内负压值的实时显示．在进行静电放电实验时,放电靶外接Tektronix数字示波器,用以对放电参数的数据采集和波形存储,该静电放电测试系统如图1所示．

在进行静电放电实验时,先打开静电放电发生器、Tektronix数字示波器和电极速度效应检测仪,对系统供电预热．将示波器的采样频率设置为10 GHz,调节控制器将步进电机转速设定为所要测量的预定值,然后用静电放电发生器设定充电电压为3 kV,为放电枪充电．拨动开启电机驱动的开关,进行静电放电实验．在电极向靶移动并与之接触放电的过程中,示波器通过同轴电缆连接放电靶,记录下放电电流数据和波形．

图1 电极速度效应静电放电测试系统

2 放电间隙局部低真空的形成机理

电极做向靶运动的过程中必然会对它周围的空气产生扰动,而且扰动的情况很复杂．根据力学的相对运动原理,电极的向靶运动可以采用相对坐标,把电极视作固定不动,气流以等同电极移动的速度迎面流来,这样去处理电极的向靶运动．其周围的气流扰动分布如图2所示．

图2 电极向靶运动过程中其周围的气流分布

根据空气动力学原理可知,在流管里,流体压强P、流体流动速度v和流体高度h之间的关系可以用Bernoulli方程来描述[13]:

(1)

式中:g是重力加速度;ρ是空气密度;c是常数．

参照图2,取A、B、C为一维流体同一流线上的不同点．电极向靶运动等效为一股平行的直匀气流迎面而来,这时气流因受电极阻碍而向周围扩散．中间会有一股细小的气流,其流速在电极的正中间A点降为零,这一点压强达到最大,记为PA．放电间隙内A、B、C三点处气体物理量压强、流速、高度等之间的关系,根据Bernoulli定律可以表示成如下形式:

(2)

式中:hA、hB、hC分别为对应点处流体离地面的高度;vA、vB、vC分别为对应点处的气流速度;PA、PB、PC分别为对应点处的气体压强．

基于Bernoulli定理,可具体分析电极移动速度对放电间隙气压的影响．考虑实验中所用放电电极的直径为12 mm,电极周围空间高度差在毫米级,A、B、C三点高度差取hC-hB≈hB-hA≈3 mm; 由于试验中电极移动速度有限,空气相对流速不大,因流速变化引起的压强变化不足以使空气密度有显著的变化,取20 ℃常温条件下的空气密度ρ为常数1.205 kg/m3; 重力加速度g=9.8 m/s2; 电极移动速度为0.5 m/s时,可取流管中三个不同点A、B、C的流速分别为vA≈0 m/s,vB≈0.25 m/s,vC≈5 m/s的情况下,则由公式(2)可得

(3)

由公式(3)可得PA>PB>PC,即电极向靶运动过程中,电极周围气体由内向外压强呈减小趋势,放电间隙整体气压减小,并且电极移动速度越快,放电间隙平均气压将越小．因此,电极向靶快速运动过程中,由于放电间隙气压降低,相对于放电间隙外部可以认为形成局部的低真空．

3 电极速度对放电参数的影响

德国柏林科技大学的S Bonisch等经过对试验的分析,建立了一种小间隙静电放电模型,该模型详细阐释了小间隙静电放电过程中的气体电子雪崩过程和电极表面发射过程．

Uncertainty evaluation of the counting of mold and yeast in cosmetics 5 37

1)电子雪崩模型

电子雪崩过程模型是根据广义Toepler定律推演而来的[14],间隙放电仅考虑快速载流子的碰撞电离．电子单位长度上碰撞电离出的电荷载流子数量由电离系数α呈现,电子迁移速度ve主要由电场强度决定．小间隙静电放电过程中,极靶间位移电流iav由放电间隙等效电容C提供能量．假设电子雪崩过程由最初数目为N0的电子所激发,则放电电流方程可描述为

(4)

式中:U是电弧电压;e是电子电荷量;d是放电弧长,通常取为放电间隙距离值．

2) 表面发射过程模型

根据Mesyats和Proskurovsky提出的计算真空脉冲放电的模型[15],表面发射过程放电电流方程可描述为

(5)

式中:K为等离子体前端屏蔽系数;me是电子质量;Sn是等离子体前面的横截面积．

已有文献给出了空气放电过程中电离系数α与压强P之间的关系以及气体介质中电子漂移速度ve依赖于磁场强度E与气体压强P的近似关系[11],关系式如下:

(6)

(7)

图3 电离系数α与气体压强P的关系

电极向靶移动放电过程中,由于电极移动速度有限,极靶空气间隙压强减小(粗真空)．环境气压未低于临界值时,随气压降低,空气密度减小,电子的平均自由程增大,有效电离增加,电离系数增大,电子雪崩过程放电电流增大．电子迁移时不仅自身获得电极速度,而且由于平均自由程增大,其无碰撞过程从电场获得的动能增大,即电子获得的平均漂移速率增大．

电极向靶运动速度越快,电极周围气压越低,参见式(6)、(7),电离系数α和电子漂移速度ve均增大,结合式(4)、(5),气隙放电中的电子雪崩过程和表面发射过程的放电电流增大．公式推演结果表明,电极向靶运动有限速度内,气压的降低,不仅有利于电子雪崩过程中有效电离的产生,还可以促进电子漂移运动．电子漂移速度增加,电子撞击电极表面时可获得更大的动能,更有利于电极表面电子的逸出,促进电极表面发射过程．同时,电极的快速向靶运动,极板间距离快速减小,进而使极板间的电场强度迅速增大,也将促进静电放电的发生．

4 实验数据的仿真分析

为探索静电放电参数受影响因素而变化的关系,使用本团队研制成功的电极移动速度效应检测仪重复多次进行试验,由带宽2.5 GHz,取样率40 G/s的Tektronix数字示波器记录下不同电极移动速度条件下的静电放电电流波形数据．观察静电放电试验数据,发现电极向靶运动速度的快慢,对静电放电参数产生了显著的影响．利用Matlab数学软件提取放电电流的最大值(峰值电流),并计算出电流脉冲的平均上升速度和平均下降速度．电极不同移动速度静电放电试验所获得的静电放电参数由表1给出．

表1 电极向靶运动速度影响下的静电放电参数

表1中放电电流参数除个别有偏差外,整体上遵循电极速度越快,放电电流峰值越大,电流脉冲平均上升速率越大,电流脉冲平均下降速率也越大这一趋势．

为了更好地研究电极移动速度与静电放电参数之间的依赖关系,分别对静电放电电流峰值、电流脉冲的平均上升速度和平均下降速度进行一次函数拟合,拟合曲线分别如图4、6、8所示,拟合函数表达式为

f(v)=av+b.

(8)

式中:v为电极移动速度;f(v)为相应的放电参数．

表2中给出了对静电放电参数进行拟合相应的函数系数取值和线性相关性参数．由表2可以看出,三种放电参数与电极移动速度相关系数绝对值均大于0.9,拟合标准差都很小,对测试结果拟合效果较好．

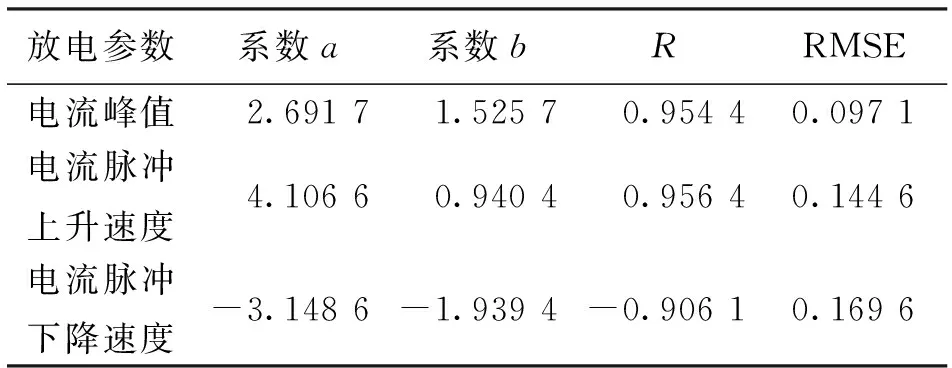
表2 放电参数拟合系数取值及相关性

注:R为相关系数; RMSE为拟合标准差(误差均方根)．

4.1 电极速度对放电电流峰值的影响

静电放电电流峰值的线性拟合关系如图4所示,随着电极移动速度的增大,电流峰值呈递增趋势．这是由于电极向靶移动速度越快,电极击穿空气放电时间越短,而放电枪充电电荷量一定,故而放电电流峰值将越大．试验结果与前面的理论推导相吻合,表明放电电流峰值与电极移动速度具有正相关性．

图4 电极移动速度与放电电流峰值的关系

4.2 电极速度对放电电流变化率的影响

为了直观地观察不同电极移动速度对放电电流脉冲变化趋势的影响,选取了四组不同电极移动速度下放电电流脉冲的平均上升速度和平均下降速度作为斜率,在同一起始点分别作直线拟合,获得不同电极移动速度下的电流脉冲上升沿趋势和下降沿趋势分别如图5和图7所示．图5中,电极向靶移动越快,放电电流脉冲上升斜率越大,电流增长速度越快．图6中,随着电极移动速度的增加,电流脉冲上升速度呈增大趋势．结果表明电流脉冲上升速度与电极移动速度具有正相关性．图7中,电极移动速度越大,放电电流脉冲下降速率越大,放电电流衰减就越快．图8中,随着电极向靶速度的增加,电流脉冲下降速度呈减小趋势．结果表明电流脉冲下降速度与电极向靶速度具有负相关性．这是由于电极快速向靶运动,极板间距离迅速缩小,电场强度迅速增大,同时放电间隙气压也迅速减小,电极所携带的电荷得以迅速释放．由式(4)、(5)可知,随着电场强度和电离系数等迅速增大,放电电流将迅速上升到峰值,这与试验测得的电流变化趋势相一致．

图5 不同电极移动速度下的电流脉冲上升沿趋势

图6 电极移动速度与电流脉冲上升速度的关系

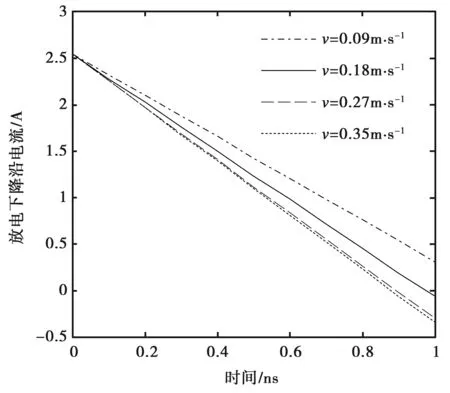
图7 不同电极移动速度下的电流脉冲下降沿趋势

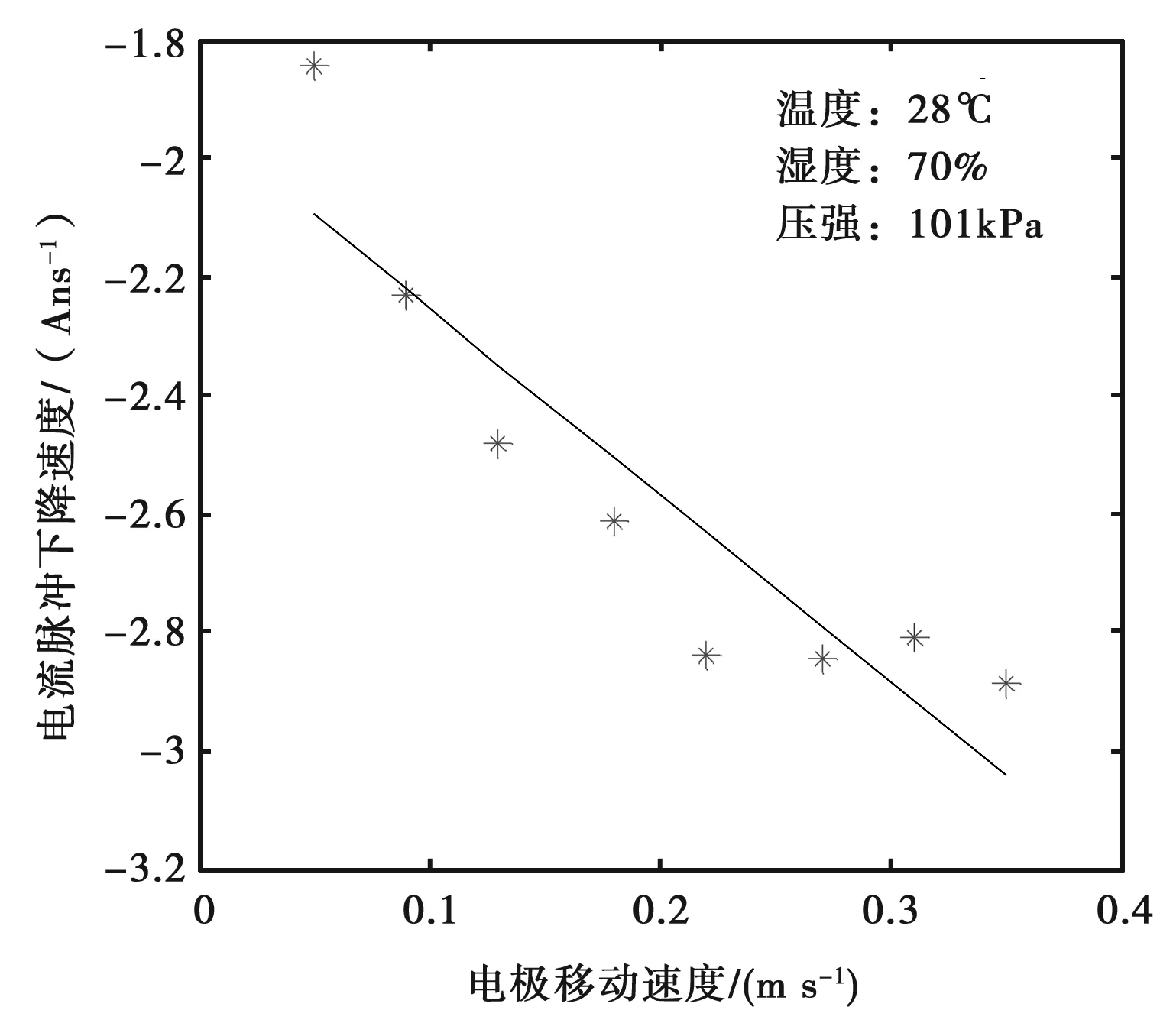
图8 电极移动速度与电流脉冲下降速度的关系

对静电放电实验数据进行仿真分析和数值处后的结果,由图5、图6、图7和图8和表2给出,其可以很好地展示电极向靶移动过程中产生的放电间隙气体压强减小效应对静电放电参数的影响．电极不同向靶移动速度下相应的四组放电电流波形由图9给出．实验结果与原理分析一致,即电极向靶速度越大,相应的电流峰值越大,放电电流的脉冲也越尖锐(电流对时间的变化率越大)．

图9 不同电极移动速度下的放电电流波形

5 结 论

就电极移动速度对静电放电参数的影响,基于大量实验数据进行了统计分析．依据空气动力学中的Bernoulli定律,分析了电极向靶移动过程中电极周围气流分布,并解释了放电间隙形成局部低真空的机理．结合帕邢定律,对电极向靶移动放电过程中放电间隙气压对放电电流的影响加以描述．考虑到电极移动速度有限,放电间隙并未形成高真空状况,所以S Bonisch等建立的小间隙静电放电的两个次级过程模型依旧适用．电极快速向靶运动,电场强度随着极靶间距的减小而增大,同时放电间隙的气体压强也随着减小,载流子将获得更大漂移速度,这就促进了气体电子雪崩过程和电极表面发射过程的作用．实验数据结果分析显示: 电极向靶移动速度与放电电流峰值、放电电流脉冲上升速度具有高度正相关性,而与放电电流脉冲下降速度具有高度的负相关性．由此充分说明,电极向靶移动速度与静电放电参数具有高度的依赖性．所得结果,对非接触静电放电标准的提出制定具有一定的参考意义．

[1] DAOUT B, RYSER H, GERMOND A, et al. The correlation of rising slope and speed of approach in ESD[C]//Proceedings of the 7th International Symposium on Electromagnetic Compatibility. Zurich, Switzerland, March 3-5, 1987: 467-474.

[2] POMMERENKE D. On the influence of the speed of approach, humidity and arc length on ESD breakdown[C]//ESD Form. Grainau, 1993: 103-111.

[3] POMMERENKE D, AIDAM M. ESD-waveform calculation, field and current of human and simulator ESD [J]. Journal of electrostatics, 1996, 38(1/2): 33-51.

[4] 原青云, 张喜军, 刘尚合, 等. 影响空气式静电放电特性的相关因素分析[J]. 高电压技术, 2010, 36(10): 2500-2506.

YUAN Q Y, ZHANG X J, LIU S H, et al. Analysis on the relative factors affecting the characteristics of air electrostatic discharge[J]. High voltage engineering, 2010, 36(10): 2500-2506. (in Chinese)

[5] RUAN F M, DLUGOSZ T. Analysis of partial vacuum formation and effect on discharge parameter in short gap ESD[J]. Electrical review, 2011, 87(2): 291-293.

[6] RUAN F M, MENG Y, XU Y B, et al. Relationship investigation of ESD parameters, air pressure variation and electrode approach speed[J]. Journal of network & information security, 2013, 4(4): 307-314.

[7] 阮方鸣, 高攸刚, 石丹, 等. 静电放电参数对电极速度的相关性与机理分析[J]. 电波科学学报, 2008, 23(5): 977-981.

RUAN F M, GAO Y G, SHI D, et al. Correlation investigation of discharge parameters with contact approach speed and its mechanism in human-metal electrostatic discharge[J]. Chinese journal of radio science, 2008, 23(5): 977-981. (in Chinese)

[8] 阮方鸣, 石丹, 高攸纲, 等. 在小间隙放电中Bernoulli定理分析电极移动速度效应[J]. 电波科学学报, 2009, 24(3): 551-555.

RUAN F M, SHI D, GAO Y G, et al. Application of Bernoulli’s theorem for speed effect of electrode moving in short-gap electrostatic discharge[J]. Chinese journal of radio science, 2009, 24(3): 551-555. (in Chinese)

[9] 阮方鸣, 董墨, 吴亮, 等. 微小间隙静电放电中两种放电模式的影响研究[J]. 电波科学学波, 2012, 27(5): 1030-1042.

RUAN F M, DONG M, WU L, et al. Effect analysis of two discharge modes on parameters in micro-gap electrostatic discharge[J]. Chinese journal of radio science, 2012, 27(5): 1030-1042. (in Chinese)

[10] RUAN F M, ZHU W, LI G C, et al. Investigation of low repeatability in parameters measurement of non-conducted electrostatic discharge[C]//Proceedings of 2014 International Symposium on Electromagnetic Compatibility (EMC Europe 2014), September 1-4, 2014: 1144-1148.

[11] 阮方鸣, 章俊华, 陈辉林, 等. 非接触静电放电测试低重复特性分析研究[J]. 电波科学学报, 2014, 29(5): 940-945.

RUAN F M, ZHANG J H, CHEN H L, et al. Analysis and investigation of low repeatability of measurement results in non-contact mode ESD[J]. Chinese journal of radio science, 2014, 29(5): 940-945. (in Chinese)

[12] BONISCH S, KALKNER W, POMMERENKE D. Modeling of short-gap ESD under consideration of different discharge mechanisms[J]. IEEE transactions on plasma science, 2003, 31(2): 736-744.

[13] 徐华舫. 空气动力学基础(上册)[M]. 北京: 国防工业出版社, 1982: 20-26.

XU H F. Fundamentals of aerodynamics[M]. Beijing: National Defence Industry Press, 1982: 20-26. (in Chinese)

[14] POMMERENKE D. Transiente Felder der ESD[D]. Berlin: Technical University Berlin, 1995. (in Germany)

[15] MESYATS G A, PRODKUROVSKY D I. Current growth in pulse breakdown of a short vacuum gap[J]. Soviet physics journal, 1968, 11(1): 81-85.

[16] 徐学基, 诸定昌. 气体放电物理[M]. 上海: 复旦大学出版社, 1996: 87-120.

XU X J, ZHU D C. Physics of gas discharge[M]. Shanghai: Press of Fudan University, 1996: 87-120. (in Chinese)

周奎 (1991-),男,河南人,贵州大学大数据与信息工程学院硕士研究生．研究方向为嵌入式系统,静电放电测试与理论．

阮方鸣 (1958-),男,贵州人,教授,北京邮电大学工学博士,IEEE Senior Member, 中国电子学会高级会员,中国通信学会高级会员,中国通信学会电磁兼容委员会委员,亚太环境电磁学术会议技术程序委员会委员．主要研究兴趣: 电磁兼容设计、静电放电、电磁生物效应、信息对抗与大数据安全．

张景 (1992-),女,山东人,复旦大学信息科学与工程学院硕士研究生,研究方向为电离层受激电磁辐射极化信号处理．

Air dynamics analysis on electrode moving speed effect

ZHOU Kui1,2RUAN Fangming2,3ZHANG Jing4SU Ming3WANG Heng3

(1.SchoolofBigDataandInformationEngineering,GuizhouUniversity,Guiyang550025,China;2.BeijingOrientalInstituteofMeasurementandTest,Beijing100094,China;3.SchoolofBigDataandComputerSciences,GuizhouNormalUniversity,Guiyang550001,China;4.KeyLaboratoryofEMWInformation,FudanUniversity,Shanghai200433,China)

The formation mechanism of partial vacuum due to electrode moving speed to the target in electrostatic discharge(ESD) process is explained based on the principle of air dynamics. Combining with double process mini-gap ESD model, the mechanism of gas pressure variation effect on parameters in ESD is discussed, and the influence of electrode moving speed on the discharge parameters is analyzed. Processing of large amount of data and simulation were performed based on experiment with our newly invented ESD measurement system, to search relationship of discharge parameters relying on electrode moving speed. Electrode moving speed, as a result, has strong positive correlation with current peak and current rise slope, but has strong negative correlation with current fall slope. The consequence of the work may provide benefit reference on proposal to non-contacted ESD test standard.

electrostatic discharge(ESD); electrode moving speed; air pressure; relativity

10.13443/j.cjors.2016082402

2016-08-24

国家自然科学基金(No. 60971078)；2016年度中央引导地方科技发展专项资金项目(黔科中引地[2016]4006号)；北京东方计量测试研究所刘尚合院士专家工作站静电研究基金(No.BOIMTLSHJD20161007);2016年度中央引导地方科技发展专项资金项目(黔科中引地[2016]4006号)

V211

A

1005-0388(2016)06-1060-07

周奎, 阮方鸣, 张景, 等. 电极移动速度效应的空气动力学分析[J]. 电波科学学报,2016,31(6):1060-1066.

ZHOU K, RUAN F M, ZHANG J,et al. Air dynamics analysis on electrode moving speed effect [J]. Chinese journal of radio science,2016,31(6):1060-1066.(in Chinese). DOI: 10.13443/j.cjors.2016082402

联系人： 阮方鸣 E-mail: ruan200145@yahoo.com

DOI 10.13443/j.cjors.2016082402