基于全天空流星雷达测量动量通量的新方法
陈金松 许莉莉 马春波 李娜 林乐科
(1.中国电波传播研究所 电波环境特性及模化技术重点实验室,青岛 266107;2.桂林电子科技大学 信息与通信学院,桂林 541004;3.中国科学院空间天气学国家重点实验室,北京 100190)
基于全天空流星雷达测量动量通量的新方法
陈金松1,3许莉莉1,2马春波2李娜1林乐科1
(1.中国电波传播研究所 电波环境特性及模化技术重点实验室,青岛 266107;2.桂林电子科技大学 信息与通信学院,桂林 541004;3.中国科学院空间天气学国家重点实验室,北京 100190)
全天空流星雷达是新一代的流星雷达,可以接收流星余迹反射的无线电波,目前主要应用于探测流星烧蚀区域的大气风场进而研究该区域的大气动力学.文中利用全天空流星雷达,基于Hocking提出的测量重力波动量通量的新方法来研究昆明地区的大气环境参数——重力波的动量通量.由于采样时间间隔的不同,该方法仍存在争议.本文主要利用昆明站工作频率为37.5 MHz的全天空流星雷达测得的流星数据来验证采样时间对重力波动量通量取值的影响,同时利用工作频率分别为37.5 MHz、53.1 MHz的全天空流星雷达在2014年9月份观测的数据对该方法进行了对比分析,结果表明:采样时间间隔的选取对重力波动量通量的取值有很大影响;在合适的采样时间间隔内利用全天空流星雷达测量重力波的动量通量的新方法是可行的.
流星余迹;大气动力学;动量通量;采样时间
引 言
微波和海洋波动中的上升表面因为地球重力的作用被向下拉回,其相邻的水表面由于相互作用而升高.水表面高度的变化随着海洋表面传播到远处,这些因为重力的原因而产生的波被称为重力波.类似的,重力波也存在于分层的大气中和海洋表面的下方,例如,我们可以看到云层沿着山脉运动,这种现象是由流体穿越山脉时在背风处产生的重力波形成的,它是产生重力波的一种典型的源,此外产生重力波的源还有很多,例如急流切变的不稳定性、积云的对流、台风、锋面气流和雷暴雨等.不像海洋表层,大气边缘没有那么明显,因此重力波的形成处在较低纬度,然后传播到上层,在重力波上升至中高层大气的过程中,其振幅会逐渐增大,直到重力波破碎或者消散,重力波的破碎或者消散会导致能量向大气的传输,其结果严重影响了大气风场和温度场的结构.此外,波破碎时所产生的扰动会引起热量的垂直传输和大气中较小成分的混合,当局部大气温度梯度比绝热下降速率大时会产生对流不稳定性.造成重力波不稳定性的原因通常假定有两种情况:一种是高频区域对流不稳定性,另一种是低频区域切变不稳定性.在重力波不稳定性发生的高度,重力波的振幅停止增大从而达到最大的状态.波振幅和质量的乘积是重力波所承载的动量,此外,动量和重力波垂直流量变化的乘积是重力波向上传播时所承载的动量通量[1-2].
传统的重力波动量通量参数的测量方法为:利用甚高频(VeryHighFrequency,VHF)雷达或中频(MediateFrequencyRadar,MF)雷达发射的对称、相对较窄的共面双波束来实现重力波参量的直接测量[3-5].Vincent、Reid等人在利用多普勒雷达测量澳大利亚阿德莱德地区的大气环境参数的分析中得出:重力波动量通量u′w′随高度平缓的变化,最大值出现在夏天和冬天的月份中[6];Tsuda在利用MU雷达(35°N,136°E)观测中高层大气环境中得出:重力波的纬向动量通量呈现明显的半年变化,在7、8月份出现东向最大值,在12-2月份出现西向最大值[7].由于在传统的测量重力波动量通量的方法中用到的雷达设备在季节和高度覆盖范围等方面局限性较大[7-10],Hocking曾提出了一种基于流星雷达观测重力波动量通量的新方法[11].流星雷达是最近十几年发展起来的探测中高层大气的重要工具,它通过观测流星余迹的反射回波来反演该区域的大气环境参数,流星雷达不受天气的影响和昼夜空间环境的限制,可以进行全天候持续性的观测[13].该方法的正确性与否仍存在争议,Vincent提出不同采样时间间隔对重力波动量通量的影响很大,可能会导致Hocking提出的计算重力波动量通量新方法的错误性[14].
中国电波传播研究所在昆明站(25.6°N,103.8°E) 建设了低纬地区大气雷达综合观测系统,通过该系统实现昆明地区大气环境参数的观测,其中包括一台工作频率为37.5MHz的全天空流星雷达和一台工作频率为53.1MHz的平流层-对流层(StratosphereandTroposphere,ST)雷达,ST雷达除了具有平流层和对流层的观测能力外,还有一个全天空流星雷达的观测模式.本文利用这两台雷达在全天空流星雷达的观测模式下得到的流星数据,基于Hocking提出的测量重力波动量通量的新方法,对昆明地区的大气环境参数进行了分析.在本文中,首先通过比较两台不同频率雷达采用不同时间间隔的计算结果,分析采样时间间隔对动量通量的影响,其次利用工作频率为37.5MHz的全天空流星雷达测得的数据反演得到了2011-2014年动量通量的年变化.
1 数据及分析方法
1.1 流星雷达数据介绍
当流星体进入大气层之后会与大气层中的分子发生剧烈的碰撞,从而使流星体加热,同时会导致流星原子从流星体的表面撞出,进而发生流星物质的激溅.当流星体加热到一定程度的时候,流星体的表面会发生气化作用,在流星体的尾部由气化作用和激溅产生的物质会继续与大气中的分子碰撞,最终会在流星尾部电离形成一条等离子体柱,称这条等离子体柱为流星余迹[15-16].
本文利用全天空流星雷达观测到的流星余迹的瞬时速度反演重力波动量通量值.根据流星数据统计,全天空流星雷达平均每天观测到的流星回波数量约为三万个,按照流星余迹回波准则对观测到的数据进行筛选[13],得到每天可用于数据分析的流星数量约为10 000~20 000个,通过流星余迹回波的到达角和距离,可以得出流星的主要分布高度范围为70~110km.在高度范围为60~110km处,工作频率为37.5MHz的全天空流星雷达9月7日一天内共探测到17 760个流星,工作频率为53.1MHz的全天空流星雷达共探测到了16 467个流星,图1给出了经过流星余迹回波准则筛选后得到的用于数据分析的流星速度随高度的分布情况,工作频率为37.5MHz的全天空流星雷达共探测到的可用于数据分析的流星个数为13 926,工作频率为53.1MHz的全天空流星雷达共探测到的可用于数据分析的流星个数为11 152.

(a) 工作频率为37.5 MHz

(b) 工作频率为53.1 MHz图1 流星速度随高度的分布情况
1.2 全天空流星雷达观测重力波动量通量原理
传统的测量重力波动量通量的方法主要依赖于雷达发射的同一垂直平面的两波束(在相反方向具有θ的倾斜角),假设两波束分别位于+x和-x轴方向,位于+x轴的波束的瞬时多普勒速度为
(U+u′)sinθ+(W+w′)cosθ.
(1)
位于-x轴的波束的瞬时多普勒速为
-(U+u′)sinθ+(W+w′)cosθ.
(2)
则两波束的均方差为

(3)


(4)


(5)
二者的均方差值即为由重力波引起的波动值.

(6)
式中:vrad是测得的流星多普勒速度值;vradm是平均多普勒速度,对于一个位于球坐标系中(θ,φ)处的流星,其瞬时多普勒速度为
vradm=Usinθcosφ+Vsinθsinφ+Wcosθ.
(7)
将式(5)、(6)、(7)带入式(4),可得到等式(8):

v′2sin2θsin2φ+w′2cos2θ+
2u′v′sin2θcosφsinφ+
2u′w′sinθcosθcosφ+
2v′w′sinθcosθsinφ]2.
(8)

(9)
1.3 平均风的计算
由式(6)可以看出平均风的取值是影响重力波动量通量值的重要因素,流星瞬时多普勒速度的方向余弦表达式为
vradm=usinθcosφ+vsinθsinφ+wcosθ.
(10)
式中:θ表示天顶角;φ表示方位角.在给定的采样区间内对等式(10)进行最小二乘拟合得到平均多普勒速度vfitm,以最小二乘拟合得到的平均多普勒速度vfitm为基准,与采样区间内各个流星的瞬时多普勒速度值比较,若存在差值大于25 m/s的流星多普勒速度,则从采样区间内剔除该值,形成一个新的采样区间,在新的采样区间内,利用最小二乘拟合得到一个新的平均多普勒速度vfitm1,继续与此采样区间内各流星的多普勒速度比较,以此方法重复进行剔除,直到所有流星的瞬时多普勒速度与平均多普勒速度的差值小于25 m/s,即得到所要求得的平均多普勒速度vradm.图2给出了由工作频率分别为37.5 MHz、53.1 MHz的全天空流星雷达测得的数据拟合得到的不同采样时间间隔时的平均风.图3中给出了不同采样时间间隔时平均风的均值与均方差,从图中可以看出拟合得到的平均风差别很小,随

图2 不同采样时间间隔(t)时平均风取值

图3 不同采样时间间隔时平均风的均值与均方差
着采样时间间隔的增加,均方差减小,在采样时间间隔为4小时时得到最优值,当采样时间间隔增大,均方差变大.根据流星余迹回波准则对观测到的流星数据进行筛选,图4给出了不同采样时间间隔时88km用于数据处理的流星分布图,从图中可以看出流星速度主要分布范围为20~40km/s.


图4 不同采样时间间隔时88 km处用于数据处理的流星分布
2 数据分析与讨论
重力波动量通量的取值主要依赖于垂直方向上的多普勒速度,因此在数据分析中排除了天顶角取值大于45°的数据,利用可发射双波束的雷达计算动量通量的传统方法中,当两波束的夹角为10°~15°时,垂直多普勒速度和水平多普勒速度在决定动量通量值时占的比率为4∶1,当夹角为30°时,二者比率为1.7∶1,当夹角为45°时,二者比率为1∶1[12].
为了验证Hocking得到的测量重力波动量通量新方法的正确性,本文首先对昆明站建设的工作频率为37.5MHz的全天空流星雷达测得的数据进行分析.通过对数据的分析发现在88km的高度范围流星出现频率达到峰值,因此我们选取了高度为88km处的流星数据进行分析.图5给出了昆明站观测到的2014年9月10-14日5天时间内88km高度处采样时间间隔为1小时的纬向平均风、径向平均风和动量通量的取值情况.从图5(a)可以看出,平均风具有明显的潮汐现象,利用最小二乘法拟合得到的多普勒速度平均风值的变化趋势与纬向、径向平均风的变化趋势也是一致的.在图5(b)中可以看出v′2存在小于0的值,v′2出现负值是不合理的,但是由于在给定的1个小时的采样时间间隔内流星采样速率小于30,从而产生了图5(b)中的v′2小于零的值.由此可以看出采样时间间隔是影响重力波动量通量取值的重要因素,计算动量通量时在给定的采样时间间隔内可用流星数必须大于30,流星雷达特定时间间隔内可用流星数与雷达单位系统参数,如频率和发射功率等、雷达位置、季节和地方时有关.图5(c)、(d)给出了剔除了采样频率过低时动量通量的取值.
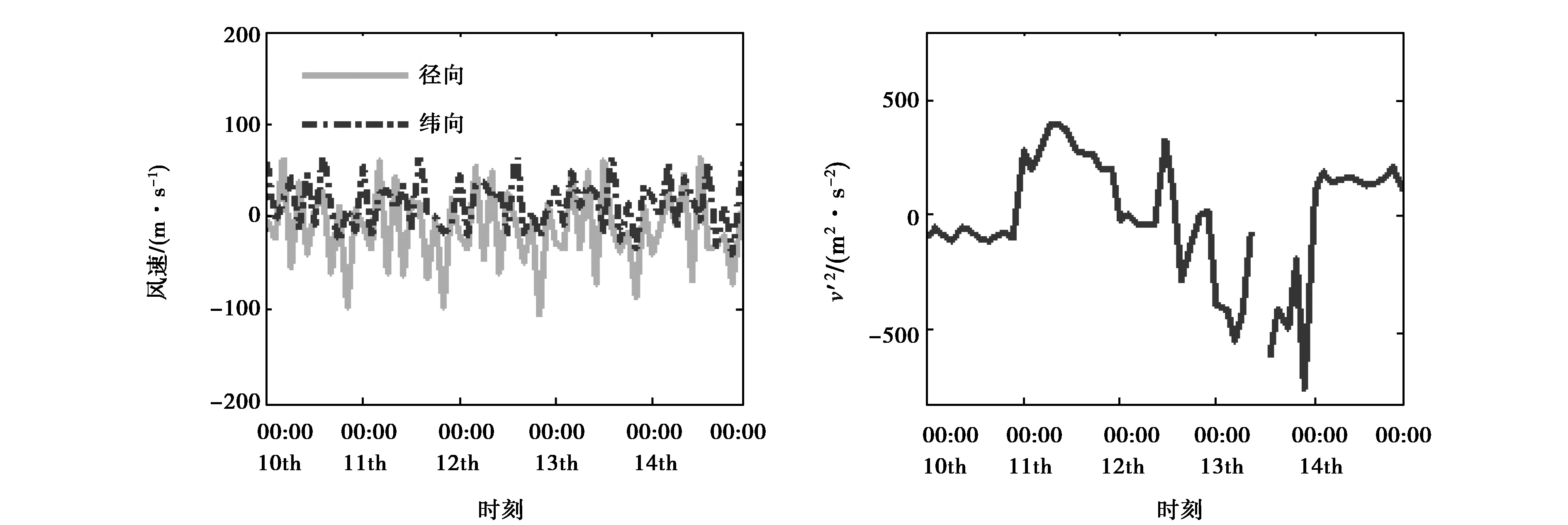
(a) (b)

(c) (d)图5 昆明站88 km高度处2014年9月10到14日采样时间间隔为1小时的 纬向平均风、径向平均风和动量通量值(横坐标为每日0点)

(a)

(b) 图6 昆明站88 km高度处2014年9月采样时间 间隔为2小时时动量通量的取值
图6中给出了测得的2014年9月份30天的重力波动量通量的取值情况,在此次分析中采样时间间隔为2小时,在给定的2小时的采样时间间隔内流星数量基本满足大于30,从图6(a)中可以看出v′2的取值大部分为正,从而验证了采样时间间隔的选取对重力波动量通量的重要性.
为了进一步验证Hocking提出的测量重力波动量通量新方法的正确性,利用昆明站两台不同工作频率的全天空流星雷达在2014年9月10-16日一周的数据进行分析,图7中分别给出了88 km处不同采样时间间隔时重力波动量通量u′w′的取值情况,由图7可以看出,两台不同工作频率(37.5 MHz、53.1 MHz)的全天空流星雷达测得的动量通量变化趋势是一致的,从图8可以看出随着采样时间间隔的增加,u′w′取值的吻合度变高,且在4小时时出现均方差最小的情况,之后随着采样时间间隔的增加,均方差变大,由此说明了采样时间间隔是影响重力波动量通量取值的重要因素.

图7 昆明站88 km高度处2014年9月不同采样时间间隔(t)时的动量通量值(实线:37.5 MHz、虚线:53.1 MHz)

图8 不同采样时间间隔时u′w′均值与方差 (实线:均方差值,虚线:均值)
图9给出了重力波动量通量u′w′在2011-2014年全年的变化情况,由于全天空流星雷达自身工作原因,在2011年1、2、3月份,2014年9、10月份无数据.从图中可以看出,2011-2013年的变化趋势比较一致,都是在夏季出现最大值,在冬季出现最小值.而2014年的最大值出现在3-5月份,最小值出现在9-11月份,都呈现比较明显的季节变化.

图9 2011-2014年东向垂直动量通量u′w′的年变化分布
3 结 论
本文利用中国电波传播研究所在昆明观测站建设的两台不同工作频率的全天空流星雷达于2014年的观测数据,基于Hocking提出的测量重力波动量通量的新方法,主要反演分析了昆明上空88 km高度处不同采样时间间隔时的动量通量,对比发现不同的采样时间间隔对重力波动量通量的影响很大,当采样时间间隔为4 h时可以得到最优结果,流星采样速率必须满足一定的条件才能保证结果的正确性; 对两台不同工作频率的全天空流星雷达观测到的动量通量值比较,在合适的采样时间间隔内,Hocking提出的新方法适用于重力波动量通量的分析.今后,还需要进一步将流星雷达的结果与其他方法比较,如中频雷达和卫星数据等,以进一步验证该方法的科学正确性.
致谢:感谢中国电波传播研究所昆明观测站提供的全天空流星雷达资料和数据.
[1] FUKAO S, HAMAZU K. Radar for meteorological and atmospheric observations[M]. Tokyo: Springer, 2014: 451-463.
[2] VINCENT R A. Introduction to atmospheric and ionospheric physics and radiowave propagation in a weak plasma[D]. Adelaide: University of Adelaide, 2014: 62-66.
[3] KUDEKI E, FRANKE S J. Statistics of momentum flux estimation [J]. Journal of atmospheric and solar-terrestrial physics, 1998, 60(16):1549-1553.
[4] THORSEN D, FRANKE S J, KUDEKI E. Statistics of momentum flux estimation using the dual coplanar beam technique[J]. Geophysical research letters, 2000, 27(19):3193-3196.
[5] THORSEN D, FRANKE S J, KUDEKI E. A new approach to MF radar interferometry for estimating mean winds and momentum flux[J]. Radio science, 1997, 32(2):707-726.
[6] REID I M, VINCENT R A. Measurements of mesospheric gravity wave momentum fluxes and mean flow accelerations at Adelaide, Australia[J]. Journal of atmospheric and terrestrial physics, 1987, 49(5):443-460.
[7] TSUDA T, MURAYAMA Y, YAMAMOTO M, et al. Seasonal variation of momentum flux in the mesosphere observed with the MU radar[J]. Geophysical research letters, 1990, 17(6):725-728.
[8] REID I M, VINCENT R A. Measurements of mesospheric gravity wave momentum fluxes and mean flow accelerations at Adelaide, Australia[J]. Journal of atmospheric and solar-terrestrial physics, 1987, 49(5): 443-460.
[9] VINCENT R A, REID I M. HF Doppler measurements of mesospheric gravity wave momentum fluxes[J]. Journal of atmospheric sciences, 1983, 40(5): 1321-1333.
[10] THORSEN D, FRANKE S J, KUDEKI E. Statistics of momentum flux estimation using the dual coplanar beam technique[J]. Geophysical research letters, 2000, 27(19): 3193-3196.
[11] HOCKING W K. A new approach to momentum flux determinations using SKiYMET meter radars[J]. Annales geophysicae, 2005, 23(7): 2433-2439.
[12] LINDEN R S. Turbulence and stress due to gravity wave and tidal breakdown[J]. Journal of geophysical research oceans, 1981, 86(C10): 9707-9714.
[13] HOLDSWORTH D A, REID I M, CERVERA M A. Buckland park all-sky interferometric meteor radar[J]. Radio science, 2004, 39(5): 267-281.
[14] VINCENT R A, KOVALAM S, REID I M. Gravity wave flux retrievals using meteor radars[J]. Geophysical research letters, 2010, 37 (14): 227-235.
[15] 陈金松. 武汉流星雷达在空间环境探测中的应用研究[D]. 北京:中国科学院,2005.
CHEN J S. An application study of the Wuhan meter radar in space environment sounding [D]. Beijing: Chinese Academy of Sciences, 2005.(in Chinese)
[16] 易稳. 流星雷达探测临近空间大气新技术的研究[D]. 桂林:桂林电子科技大学, 2014.
YI W. A study of new technology for near space atmosphere detection by meter radar[D]. Guilin: Guilin University of Electronic Technology, 2014.(in Chinese)
A new method of determining momentum flux based on the all-sky meteor radar
CHEN Jinsong1,3XU Lili1,2MA Chunbo2LI Na1LIN Leke1
(1.NationalKeyLaboratoryofElectromagneticEnvironment,ChinaResearchInstituteofRadiowavePropagation,Qingdao266107,China;2.SchoolofInformationandCommunication,GuilinUniversityofElectronicTechnology,Guilin541004,China;3.StateKeyLaboratoryofSpaceWeather,ChineseAcademyofScience,Beijing100190,China)
The all-sky meteor radar is the newest generation of meteor radars, which can receive the radio waves reflected by meteor echoes. At present, the main objects observed by the modern meteor radar is the atmospheric wind fields in the meteor region, with the purpose of research atmospheric dynamics. This thesis utilizes all-sky meteor radar based on a new method which is used for determining momentum flux by Hocking to research atmospheric parameters, namely as the momentum fluxes of gravity waves. Because of the difference of sampling time, this new method is still controversial. We mainly use the data collected by the all-sky meteor radar operated at 37.5MHz to validate the influence of sampling time on gravity momentum fluxes. Meanwhile, we use data collected by the all-sky meteor radar with different frequencies (37.5MHz and 53.1MHz) during September 2014 to verify the correctness of the new method improved by Hocking. The results show that: the choice of sampling time greatly influences the determination of gravity waves; and with suit sampling interval, it is viable to determine gravity wave momentum fluxes using the new method based on all-sky meteor radar.
meteor echoes; atmospheric dynamics; momentum flux; sampling interval
10.13443/j.cjors.2015123002
2015-12-30
国防科技重点实验室基金项目(A171401Z11); 国家自然科学基金(41604129)
P351
A
1005-0388(2016)06-1124-08
陈金松 (1979-),男,湖北人,中国电波传播研究所高级工程师,主要从事中高层大气的探测与研究.
许莉莉 (1991-),女,山东人,桂林电子科技大学硕士研究生,主要从事信号处理方面的研究.
马春波 (1975-),男,广西人,桂林电子科技大学教授,主要从事通信信号处理、光通信方面的研究.
陈金松, 许莉莉,马春波,等. 基于全天空流星雷达测量动量通量的新方法[J]. 电波科学学报,2016,31(6):1124-1131.
CHEN J S, XU L L, MA C B, et al. A new method of determining momentum flux based on the all-sky meteor radar[J]. Chinese journal of radio science,2016,31(6):1124-1131. (in Chinese). DOI: 10.13443/j.cjors.2015123002
联系人: 陈金松 E-mail 63555190@qq.com
DOI 10.13443/j.cjors.2015123002

