地海交界分区域复合粗糙面的布儒斯特效应研究

邹高翔 童创明,2 孙华龙 王童 彭鹏,3

(1.空军工程大学防空反导学院,西安 710051;2.东南大学 毫米波国家重点实验室,南京 210096;3.西安电子科技大学物理与光电工程学院,西安 710071)

地海交界分区域复合粗糙面的布儒斯特效应研究

邹高翔1童创明1,2孙华龙1王童1彭鹏1,3

(1.空军工程大学防空反导学院,西安 710051;2.东南大学 毫米波国家重点实验室,南京 210096;3.西安电子科技大学物理与光电工程学院,西安 710071)

通过随机粗糙面建模理论,研究地海交界分区域复合粗糙面的布儒斯特效应．采用蒙特卡罗方法,利用高斯谱函数模拟陆地粗糙面,利用Pierson-Moskowitz(PM)海洋谱模拟海面部分,运用加权反正切函数滤波处理以平滑交界,构建了地海交界分区域复合粗糙面的几何模型．考虑到粗糙陆地表面与海面各自内部面元的耦合作用以及区域之间和交界处面元的相互耦合,提出了一种基于地海交界分区域面元的迭代物理光学法,快速求解地海交界分区域复合粗糙面的镜向散射,分别就陆地粗糙面的均方根高度、相关长度,海面的风速、风向对其布儒斯特效应的影响进行了分析,发现了地海交界分区域复合粗糙面上的“布儒斯特融合效应”,并发现陆地粗糙面的均方根高度与海面风速能够显著影响布儒斯特角的“融合”现象．本研究为探测地海交界区域的真实环境提供了理论基础,数值仿真结果对抗多径干扰、雷达目标的探测与识别、遥感信息处理具有借鉴意义．

地海交界;分区域复合粗糙面;迭代物理光学法;布儒斯特效应

引 言

近年来,随着计算电磁学的高速发展,随机粗糙表面电磁散射特性的研究已经成为了许多学者研究的热点,在雷达成像、薄膜物理、材料科学和军事领域等均有广泛的应用[1-4]．在已有的随机粗糙面散射研究中,许多学者采用不同统计特性的谱函数来模拟真实的自然环境,如采用高斯谱函数模拟实际地面[5-6],采用PM谱函数模拟实际海面[7-8]等,这些通常采用单一统计特性的谱函数来生成单一类型的随机表面,然而在自然界中的真实地表往往是复合且多统计特性的,本课题组曾对分区域复合粗糙面的建模理论[9]进行了研究,利用高斯谱函数结合反正切权函数滤波处理实现了表面粗糙度不同分区域复合粗糙面,解决了分区域复合环境的建模问题．

布儒斯特效应是指垂直极化波以特定角度照射光滑的介质平面,出现镜面反射波为零的现象．对于平面散射问题中布儒斯特效应的研究,已经有确定的公式对其进行准确的描述．国外学者在研究粗糙面散射问题时发现,粗糙面的散射同样存在着布儒斯特效应．文献[10]中通过数值方法研究一维粗糙表面时发现粗糙面的布儒斯特角相比于水平面,会存在一定的偏移;文献[11]在这一现象上,采取解析法运用拟合的方式分析出布儒斯特角的偏移与粗糙面均方根高度和相关长度的关系;文献[12]又进一步将这一问题拓展到了二维粗糙表面上;文献[13]研究了入射频率、海水介电常数与布儒斯特角的关系;文献[14]通过布儒斯特角的测量,估算出了介质粗糙面介电常数,将该项研究推向了应用领域．国内方面,本课题组曾针对超低空探测中存在的多径干扰问题,提出“广义布儒斯特效应”,以降低多径干扰的影响[15]．综上所述,已有的关于粗糙面布儒斯特效应的研究对象,多为单一随机粗糙面,然而自然界中的真实地表往往是复合且多统计特性的,区别于以往学者们针对单一随机粗糙面的布儒斯特效应的研究,本文针对地海交界环境,研究了地海交界分区域复合粗糙面的布儒斯特效应,目前国内外尚未检索到研究地海交界环境布儒斯特效应的相关文献．

在研究环境粗糙表面散射中,物理光学(Physical Optics,PO)法具有计算速度快、计算机存储量少的优点,然而PO法是基于基尔霍夫近似条件(KA)的近似方法,当入射波的波长λ和粗糙面表面曲率半径ρ无法满足条件ρ≫λ时,必须考虑粗糙面面元间的相互耦合作用,需引入迭代物理光学(Iterative Physical Optics, IPO)法[16-22]对这类问题进行分析．迭代物理光学法最先被应用于开口腔体电磁散射特性的分析[16];随后,又被应用于粗糙表面的电磁散射[17-18]与复杂结构目标散射特性的分析[19-20],这种方法充分考虑到面元之间的相互耦合,在表面电流迭代的过程中表现出良好的收敛性．近几年,有学者将IPO与快速多极子(Fast Multipole Mehod,FMM)、多层快速多极子(Multilevel Fast Multipole Mehod,MLFMM)技术相结合[21-22],应用于加速求解粗糙面及其上方目标的复合散射．但运用IPO对地海交界分区域复合粗糙面的散射求解,目前国内外尚未检索到相关文献．区别于文献[17-18]基于粗糙表面面元电流的迭代,对于地海交界分区域复合粗糙面,其表面介质的复折射率不一定满足阻抗边界条件,因此必须采用表面面元电流、磁流的共同迭代来求解其散射问题．

在本课题组已有的分区域复合粗糙面的建模理论中,仅采用高斯谱函数,无法准确地描述地海交界环境随机表面的统计特性,本文则在此基础之上,同时采用高斯谱与PM谱函数,提出了地海交界分区域复合粗糙面建模方法,完善了分区域复合环境的建模理论;并针对地海交界分区域复合粗糙面的双重属性和复合性,考虑到粗糙陆地表面与海面各区域内部面元的耦合作用以及区域之间和交界处面元的相互耦合,提出了一种基于地海交界分区域面元的迭代物理光学法,快速求解地海交界分区域复合粗糙面的镜向散射;分析了其布儒斯特效应的内在规律,为雷达武器预研评估提供理论基础,相应的仿真结果,能够应用于地海交界环境下,当防空武器及预警机雷达探测超低空目标时,能够通过布儒斯特角以垂直极化波下视探测,最大程度地减少环境所带来的多径干扰,增强雷达在地海交界环境下的超低空目标探测能力．

1 理论分析

1.1 陆地粗糙面建模

引入高斯谱用来模拟分区域复合粗糙面的陆地粗糙面部分．陆地粗糙面的高度轮廓函数f(x,y)用快速傅里叶变换表示为

(1)

式中,二维高斯粗糙面的系数为

(2)

其中高斯谱函数的表达形式为

(3)

式中:hrms为均方根高度;lx和ly为x和y方向的相关长度．N(0,1)为均值为零,方差为一个呈正态分布的随机数序列的一个采样点;Kxm、Kyn分别为x、y方向的空间频率的离散点,Lx、Ly分别为粗糙面在x、y方向的轮廓长度,Nx、Ny分别是粗糙面在x、y方向的采样点个数,关系如下

(4)

1.2 海面建模

海面从本质上均属于粗糙面的范畴．为使模型构建准确,在本文的研究中,使用经典的PM海谱生成海面,用以模拟分区域复合粗糙面的海面部分．二维PM海谱表达式为

(5)

式中:α和β是无量纲经验常数,α=8.10×10-3,β=0.74;gc是重力加速度,gc=9.81 m/s2;v19.5是海面上方19.5 m高度处的风速;Φ(φ)为扩散函数,一般取

(6)

φ为xoy面内的方位角,φv表示风向,φv=0时表示风向沿x正方向．在直角坐标系下有

(7)

于是,在直角坐标系下PM谱函数变为

(8)

将式(8)代入式(2)作为式(1)中的系数bmn,并将其代入式(1)即得到二维海面的高度起伏轮廓．

1.3 分区域复合粗糙面建模理论

传统的谱函数只能模拟单一类型的随机粗糙面,而真实的地海交界环境表面通常是既具备陆地粗糙面又包含海面的,为了贴近真实的地海交界环境中的地理轮廓和地形结构,采用高斯谱函数和Pierson-Moskowitz海洋谱函数,利用MonteCarlo方法,生成同时具备两种统计特性的随机粗糙面,在交界处采用加权反正切函数平滑处理,生成地海交界分区域复合粗糙面．

该建模方法的理论基础为:

1) 陆地区域随机表面的统计特性可由均方根高度hrms和相关长度lx,ly来描述;

2) 海面区域随机表面的统计特性可由海面上方19.5 m高度处的风速v19.5和风向φv来描述;

3) 以Monte Carlo方法模拟生成粗糙面实质上是对线性滤波后的谱密度函数进行逆傅里叶变换,从而得到粗糙面的高低起伏;

4) 以反正切函数为权函数进行的功率谱调制,可以既保持不同粗糙区域的统计特征不被改变,又能在不同区域的交界处实现平滑衔接．

利用加权反正切函数对交界处进行平滑处理,实质上就是对线性系统中频谱的调制．加权反正切函数表达式如下

fcom(x,y)=fsur1(x,y)·[π/2+

arctanfw(x,y)]/π+fsur2(x,y)·

[π/2-arctanfw(x,y)]/π.

(9)

式中:fsur1(x,y)、fsur2(x,y)和fcom(x,y)分别表示分区域表面sur1、sur2和分区域复合粗糙面的高低起伏轮廓,fw(x,y)为边界调制权函数,其形式将根据具体所需生成的表面结构来确定．加权反正切函数平滑处理效果如图1所示．

图1 加权反正切函数平滑处理效果图

1.4 地海交界分区域复合粗糙面建模

海洋和陆地是地球表面的两个基本单元,地海交界环境就是既包含陆地粗糙面,同时也包含海面的自然环境,具有复合性、分区域性和复杂性的特点．在实际的自然环境中,陆地与海洋的分界线大多数呈现为近似线性的边界,因此本文将其简化为直线型边界,构建地海交界分区域粗糙面的几何模型．

传统的谱函数只能模拟单一类型的随机粗糙面,而本文所研究的地海交界环境不仅含有陆地粗糙面,同时也包含海面．因此,同时采用两种谱函数分别在不同区域生成粗糙面,在其交界处采用加权反正切函数平滑处理,加权反正切函数表达式如下

fcom(x,y)=w1·fgro(x,y)+w2·fsea(x,y)，

(10)

式中：fgro(x,y)和fsea(x,y)分别表示陆地粗糙表面和海面粗糙表面的高低起伏轮廓；yb为地海交界的位置,也可以取xb方向,根据实际情况而定．通过调整yb的位置,能够调整分区域复合粗糙面陆地与海面的比例．设置参数yb=0,即陆海表面面积比例为1∶1,工作频率f=300 MHz,地海交界分区域粗糙面大小取Lx×Ly∶2 km×2 km,陆地粗糙面统计参数为hrms=1.0λ,lx=ly=1.0λ;海面统计参数为v19.5=0.5 m/s,φv=0°．每个波长取5个采样点,仿真图像如图2所示,其中图2(a)展示了所生成的地海交界分区域复合粗糙面的几何结构,图2(b)展示了各谱函数所模拟的陆地粗糙面与海面高度起伏轮廓所代表的区域、边界选取的位置、粗糙面的尺寸以及地海交界分区域粗糙面在直角坐标系中的取向．

(a) 直线型边界几何结构

(b) 地海交界环境仿真图图2 地海交界分区域复合粗糙面仿真图像

在真实的自然环境,陆地与海洋的交界往往是随机和非线性的,本文着重点是研究这类具备分区域特性环境的散射特性,因此将其交界处简化为上述确知函数．我们也可以采取多种不同的加权反正切函数来模拟更加复杂的交界部位．

1.5 基于分区域面元的迭代物理光学法

在研究环境粗糙表面散射中,PO法具有计算速度快、计算机存储量少的优点,PO法是基于基尔霍夫近似条件(KA)的近似方法,其基本思想是当入射波的波长λ和粗糙面表面曲率半径ρ满足条件:ρ≫λ时,粗糙面可视为由许多小平面拼接而成．PO法被广泛应用于分析大尺度、相对平坦的粗糙面散射问题中．然而,当粗糙表面变得更为粗糙,λ和ρ无法满足上述条件,并且粗糙表面具备多重介质属性,则表面边缘、尖点的散射,以及各介质区域内部的面元耦合以及区域之间和交界处面元的耦合作用将不可忽略,需引入迭代物理光学法[17-18]．迭代物理光学法是以Stratton-Chu公式所推导的表面电场积分程(Electric Field Integral Equation,EFIE)和表面磁场积分程(Magnetic Field Integral Field,MFIE)为基础,其核心是进行感应电流和感应磁流的迭代,得到满足迭代误差的感应电流和感应磁流,从而求得散射场．

由于地海交界分区域复合粗糙面的研究对象是不同介质的陆地表面和海面,表面介质的复折射率不一定满足阻抗边界条件,因此必须采用电流、磁流的共同迭代．积分方程的主值形式分别为

E(r)= 2Ei(r)+∫S-ΔS{-jωμ0[J(r′)g(r,r′)+

(11)

H(r)= 2Hi(r)+∫S-ΔS{-jωε0[M(r′)g(r，r′)+

(12)

式中:Ei(r)为入射电场;Hi(r)为入射磁场;k为自由空间波数;g(r,r′)为自由空间的格林函数．

(13)

为了消除粗糙面的边缘突然被截断而产生的反射和边缘绕射等效应,用锥形入射波代替平面波入射,参考文献[23],设置波束宽度g与粗糙面尺寸Lx、Ly为式(14),能获得合理的计算结果和较快的效率．

(14)

i=1,2,…,N；

i=1,2,…,N.

(15)

式中:

(16)

用PEij(·)、PMij(·)表示复合积分,用来代替式(11)、(12)右边的积分项,表达式为

{-jωμ0[J(r′)g(r,r′)+

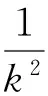
M(r′)×g(r,r′)}dS′,r∈S.

(17)

(18)

上式为在面元Sj上的积分．考察所有面元,i=1,2,…,N,将式(11)、(12)写成矩阵向量形式．

[J]=[Jin]+[PM(J,M)];

[M]=[Min]+[PE(J,M)];

=[PM][J];

=[PE][M].

(19)

式中: [PM]为耦合电流矩阵,元素PMij中表征面元j对面元i的耦合感应电流作用;相应的,[PE]为耦合磁流矩阵,元素PEij中表征面元j对面元i的耦合感应磁流作用．[PM]、[PE]均可进行写为上三角矩阵[U]、下三角矩阵[L]与单位对角矩阵[D]相加的形式,将矩阵写为如下形式:

[D][J]=[Jinc]+([UPM]+[LPM])[J];

[D][M]=[Minc]+([UPE]+[LPE])[M].

(20)

求解未知矢量J、M时,采用Jacobi迭代方法来更新电流和磁流,第k次迭代可以表示为如下形式:

[D][J(k+1)]= [Jinc]+([UPM]+[LPM])[J(k)],

k=0,1,2,…;

[D][M(k+1)]= [Minc]+([UPE]+

[LPE])[M(k)],k=0,1,2,….

(21)

值得注意的是,进行J、M的第k+1次迭代时,矩阵[PM(k+1)]、[PE(k+1)]须使用第k次的J(k)、M(k)进行更新．

定义粗糙表面所有面元上感应电流与感应磁流的第k次迭代误差为

(22)

式中,‖·‖2表示2范数,通常设定误差收敛门达到10-2时,认为所求解的电流系数与磁流系数达到稳定,停止迭代即可得到最终的粗糙表面电磁流分布．最后,代入式(11)、(12)获得粗糙表面的电磁散射．

通过散射场计算双站散射系数时,需通过入射角所对应表面的实际被照射面积进行修正,参考文献[23],定义随机表面的双站散射为如下形式．

(23)

对于粗糙面散射特性的求解,为了保证计算的精度,在本文的每个算例中均建立50个几何模型样本,利用IPO计算出每个具体粗糙面样本的散射场,得到散射系数的集平均值作为最后的仿真结果．

1.6 算法验证

考察大入射角下,同时具备高斯谱和PM谱统计特性的地海交界分区域复合粗糙面情况下,IPO算法的有效性．设置工作频率f=300 MHz,地海交界分区域复合粗糙面大小Lx×Ly为2 km×2 km,陆地粗糙面统计参数为:hrms=1.0λ,lx=ly=1.0λ,对应频率的介电常数取εr1=(4.0,-j0.000 6); 海面统计参数为:v19.5=0.5 m/s,φv=0°,介电常数取εr2=(20.0,-j240.0); 取定每波长面积内的采样点为25个．设置入射角度为θi=60°、φi=0°,此时ρ=0.866λ,不满足KA近似条件．在锥形波照射下,计算结果与基于矩量法的快速多极子(Multilevel Fast Multipole Method,MLFMM)精确数值算法进行对比,观测角度θ范围为-90°～90°,极化方式为VV极化．本文的仿真计算均在个人计算机环境下实现,配置为主频2.6 GHz,内存4 GB．计算结果如图3所示．

图3 IPO计算分区域复合粗糙面的双站散射系数对比

如图3所示,与MLFMM结果相比较,在掠入射角区域,PO法无法得到准确的解,而IPO法在经过近10次迭代至电磁流稳定后,能够得到精确的计算结果,在计算时间上,IPO算法耗时1 052 s,而MLFMM耗时5 276 s,相比之下提高了运算效率．地海交界分区域复合粗糙面的陆地粗糙面粗糙程度较大,面元间的相互耦合加剧了各角度的能量发散,随机表面呈现出漫散射特性; 而海面区域的镜向散射特性较强,使得地海交界分区域复合粗糙面在镜向方向附近有明显峰值,这就是地海交界分区域复合粗糙面独特的散射特性．

2 布儒斯特效应仿真分析

电磁波经过地面的散射作用,电场幅度将衰减,相位将滞后,而当垂直极化波以特定角度照射的介质表面,出现镜向散射为极小值的现象,我们将其称为布儒斯特效应．介质表面布儒斯特角的位置,通常是由介质的相对介电常数和电导率来确定的,而通过近年来一些学者的研究,发现随机表面的粗糙程度也会对布儒斯特角的位置带来影响[10-12]．地海交界环境不仅包含两种介质属性,同时具有多种因素来影响其表面粗糙程度,而在这种复杂前提下对其布儒斯特效应的研究,是后文仿真分析的重点．

2.1 地海交界分区域粗糙面的布儒斯特融合效应

考察地海交界分区域粗糙面的布儒斯特效应,对比对象就是相同电尺寸的陆地粗糙面与海面的镜向散射分布．设置工作频率f=300 MHz,粗糙面的大小Lx×Ly均为2 km×2 km．陆地粗糙面统计参数为:hrms=0.1λ,lx=ly=1.0λ,对应频率的介电常数取εr1=(4.0,-j0.000 6); 海面统计参数:v19.5=0.5 m/s,φv=0°,介电常数取εr2=(20.0,-j240.0); 地海交界分区域复合粗糙面的各区域参数与上述相同,采用IPO法快速获取其镜向散射,仿真结果如图4所示．

(a) 陆地布儒斯特角

(b) 海面布儒斯特角

(c) 地海交界分区域粗糙面布儒斯特角图4 布儒斯特融合效应

众所周知,超低空突防就是借助突防武器(如战斗机、无人机和巡航导弹等)的低空、超低空飞行,使自身的雷达回波隐藏在复杂的环境回波之中,从而达到隐身的目的; 目标与环境的多重耦合所引起多路径回波的现象我们将其称为多径效应,采用垂直极化波利用布儒斯特角对超低空目标进行探测,是目前减小环境所引起的多径效应、对抗超低空突防行之有效的手段．然而,通过仿真可以发现,在地海交界环境处,布儒斯特角相对于陆地与海面均发生了剧烈变化,若此时探测雷达并未及时作出反应,超低空目标的回波便会迅速淹没在环境回波之中,致使所跟踪的目标丢失,再度延长了预警时间．

2.2 陆地粗糙面统计参数影响分析

随机表面的粗糙程度会对布儒斯特角的位置带来影响,在地海交界分区域复合粗糙面中,陆地粗糙面的粗糙程度是由统计参数均方根高度hrms和相关长度lx、ly所确定．

首先,考察均方根高度hrms对地海交界分区域复合粗糙面布儒斯特效应的影响．在文献[11]和[12]的结论中可以知道,当粗糙面的粗糙程度过大时,粗糙表面的布儒斯特效应将会消失,将不再存在明显的布儒斯特角,因此取均方根高度hrms为较小值范围,来考察其对地海交界分区域复合粗糙面布儒斯特效应的影响．设置工作频率f=300 MHz,粗糙面的大小Lx×Ly为2 km×2 km,陆地粗糙面相关长度lx=ly=1.0λ,海面统计参数为:v19.5=0.5 m/s,φv=0°,考察不同均方根高度hrms下地海交界分区域复合粗糙面的布儒斯特效应,仿真结果如图5．

如图5所示,当陆地粗糙面的均方根高度hrms分别取0.1λ、0.2λ和0.3λ时对应地海交界分区域复合粗糙面的布儒斯特角分别为φB=11.5°、φB=12.0°和φB=12.5°,随着均方根高度的增加,分区域复合随机表面的布儒斯特角增大,这是由于陆地随机表面的各向异性增强,致使陆地随机表面的布儒斯特角变大,再由于布儒斯特融合效应,影响到地海交界分区域复合随机表面的布儒斯特角的位置,导致布儒斯特角的增大．

考察相关长度lx、ly对地海交界分区域复合粗糙面布儒斯特效应的影响．设置工作频率f=300 MHz,粗糙面的大小Lx×Ly均为2 km×2 km,陆地粗糙面均方根高度hrms=0.1λ,海面统计参数为:v19.5=0.5 m/s,φv=0°,考察不同相关长度下地海交界分区域复合粗糙面的布儒斯特效应,仿真结果如图6．

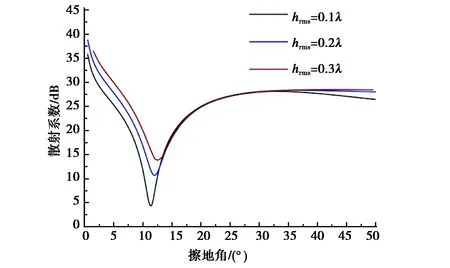
图5 不同均方根高度hrms下地海交界分区域复合 粗糙面的布儒斯特效应

图6 不同相关长度lx、ly下地海交界分区域 复合粗糙面的布儒斯特效应

如图6所示,当陆地粗糙面的相关长度l=lx=ly分别取1.0λ、2.0λ和3.0λ时对应地海交界分区域复合粗糙面的布儒斯特角φB分别为11.5°、11.2°和11.0°,随着相关长度的增加,分区域复合随机表面的布儒斯特角减小,这是由于陆地表面各点的相关性增强,各向异性减弱,致使陆地粗糙面的布儒斯特角变小,再由于布儒斯特融合效应,使得地海交界分区域复合随机表面的布儒斯特角减小．对比本节仿真结果,得到陆地粗糙面的均方根高度hrms较相关长度lx、ly对布儒斯特融合效应的影响更加显著．

2.3 海面统计参数影响分析

海面的粗糙程度是由统计参数海面上方19.5 m高度处的风速v19.5与风向φv所确定,根据国家海洋局提供的海况级别划分表(见表1),对海况等级1到3级,对应风速取v19.5=0.5 m/s、2.0 m/s和4.0 m/s情况下的海面进行研究．

考察风速v对地海交界分区域复合粗糙面布儒斯特效应的影响．设置工作频率f=300 MHz,粗糙面的大小Lx×Ly均为2 km×2 km,陆地粗糙面均方根高度hrms=0.1λ、相关长度lx=ly=1.0λ,海面风向为φv=0°,考察不同风速下地海交界分区域复合粗糙面的布儒斯特效应,仿真结果如图7．

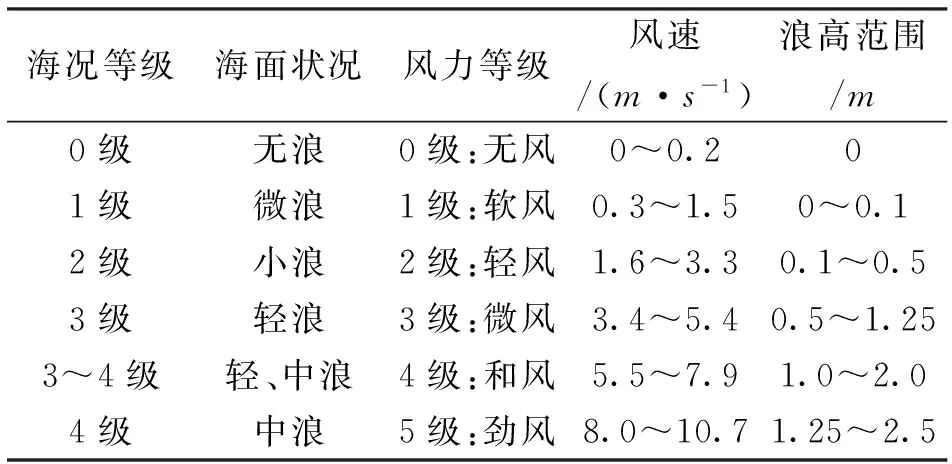
表1 海况级别划分表

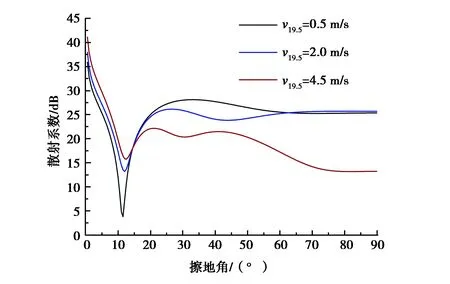
图7 不同风速v19.5下地海交界分区域复合 粗糙面的布儒斯特效应

图8 不同风向φv下地海交界分区域 复合粗糙面的布儒斯特效应

如图7所示,当海面的风速v19.5分别为0.5 m/s、2.0 m/s和4.0 m/s时对应地海交界分区域复合粗糙面的布儒斯特角分别为φB=11.5°、φB=12.0°和φB=12.5°,随着风速的增加,分区域复合随机表面的布儒斯特角增大,这是由于海面的各向异性增强和布儒斯特融合效应的共同作用,导致地海交界分区域复合随机表面的布儒斯特角增大; 然而在海况等级达到3级时,风速已经到达很高水平,海面的粗糙程度剧烈增加,再加上海水的相对介电常数与电导率在数量级上远大于陆地的相对介电常数与电导率,导致在海况等级在3级时,掠入射角度范围布儒斯特角所对应的散射系数极小的现象已经不明显,相比在大擦地角下的镜向散射系数,布儒斯特效应已经不再显著．上述结果表明,海面的风速的增加会引起地海交界分区域复合粗糙面的布儒斯特角的增大,当风速达到一定程度后,地海交界分区域复合随机表面的布儒斯特效应将不再显著．

考察风向φv对地海交界分区域复合粗糙面布儒斯特效应的影响．设置工作频率f=300 MHz,粗糙面的大小Lx×Ly均为2 km×2 km,陆地粗糙面均方根高度hrms=0.1λ、相关长度lx=ly=1.0λ,海面风速取v19.5=0.5 m/s,仿真结果如图8．

如图8所示,当海面的风向φv分别为0°和60°时对应地海交界分区域复合粗糙面的布儒斯特角φB分别为11.4°和10.3°,风向由顺风φv=0°变为侧风φv=60°时,地海交界分区域复合粗糙面的布儒斯特角变小,这是由于顺风时海面的粗糙程度大于侧风状态,海面的漫散射特性较强,再由于布儒斯特融合效应的共同作用,使得地海交界分区域复合粗糙面的布儒斯特角变小．对比本节仿真结果,得到海面的风速v19.5较风向φv对布儒斯特融合效应的影响更加显著．

3 结 论

本文的工作主要在于地海交界环境的分区域复合随机表面的建模与其散射特性快速精确获取方法的研究,是在国内外尚未检索到相关文献的基础之上,首次对地海交界分区域复合粗糙面的布儒斯特效应进行了探索与分析．在分区域复合粗糙面的建模理论上,提出了同时采用高斯谱函数和PM海谱模拟地海环境的分区域复合建模方法,为真实地海环境表面的建模提供了一定的理论参考．针对地海交界分区域复合粗糙面的双重属性和复合性,考虑到粗糙陆地表面与海面各自内部面元的耦合作用以及区域之间和交界处面元的相互耦合,提出了一种基于地海交界分区域面元的迭代物理光学法,快速求解地海交界分区域复合粗糙面的镜向散射．在此基础之上,仿真得到了地海环境处布儒斯特角的“融合”现象,将其定义为布儒斯特融合效应,并分别就地海交界分区域复合粗糙面陆地粗糙面区域的均方根高度、相关长度以及海面区域的风速、风向对布儒斯特融合效应的影响进行了讨论,得到了各区域的粗糙程度发生变化所引起的布儒斯特角的移动均会通过布儒斯特融合效应来引起整个地海交界分区域复合粗糙面的布儒斯特角的改变,以及相比之下陆地粗糙面均方根高度与海面风速能够更显著地影响布儒斯特角的“融合”现象的结论．

[1] ZILMAN G, ZAPOLSKI A, MAROM M. On detect ability of a ship's Kelvin wake in simulated SAR images of rough sea surface[J]. IEEE transactions on geoscience & remote sensing, 2015, 53(2): 609-619.

[2] NEJATI H, SARABANDI K. Theoretical analysis of tree trunk rough surface interaction using reaction theorem[J]. Journal of applied physics, 2011, 110(1): 5169-5172.

[3] CALAME J P, GARVEN M. Dielectric permittivity simulations of layered composites with rough interfacial surfaces[J]. IEEE transactions on dielectrics & electrical insulation, 2007, 14(2):287-295.

[4] VORONOVICH A G, ZAVOROTNY V U. Full-Polarization modeling of monostatic and bistatic radar scattering from a rough sea surface[J]. IEEE transactions on antennas & propagation, 2014, 62(3): 1362-1371.

[5] EL-BAH S, DUSSEAUX R, AFIFI S. Some statistical and spatial properties of signal scattering by 2-D slightly rough random surfaces[J]. IEEE transactions on antennas & propagation, 2016, 64(2):721-729.

[6] REN X C. Study on electromagnetic scattering from Gaussian rough surface of layered medium with circular polarized wave incidence[C]//Cross Strait Quad-regional Radio Science & Wireless Technology Conference, 2013: 308-311.

[7] JOEL T J, ROBERT J B, JAKOV V T, et al. A numerical study of the retrieval of sea surface height profiles from low grazing angle radar data[J]. IEEE transactions on antennas & propagation, 2009, 47(6):1641-1650.

[8] WANG R, GUO L X, WANG A Q. Study on the scattering from sea surface with PM spectrum covered by organic film[C]//IEEE International Symposium on Antennas Propagation & EM Theory, 2010:738-741.

[9] 李昌泽, 童创明, 齐立辉，等. 三类新型随机粗糙面模型的快速散射特性分析[J]. 电波科学学报, 2015, 30(6)：1093-1101.

LI C Z, TONG C M, QI L H, et al. Analysis on fast electromagnetic scattering characteristics for three novel randomly rough surface models[J]. Chinese journal of radio science, 2015, 30(6):1093-1101.(in Chinese)

[10] SAILLARD M, MAYSTRE D. Scattering from metallic and dielectric rough surfaces[J]. Journal of the optical society of America A, 1990, 7(6):982-990.

[11] GREFFET J J. Theoretical model of the shift of the Brewster angle on a rough surface[J]. Optics letters, 1992, 17(4):238-40.

[12] BAYLARD C, MARADUDIN A A, GREFFET J J. Coherent reflection factor of a random rough surface: applications[J]. Journal of the Optical Society of America A, 1993, 10(12):2637-2647.

[13] TRIZNA D B. Model for Brewster angle damping and multipath effects on the microwave radar sea echo at low grazing angles[J]. IEEE transactions on geoscience & remote sensing, 1997, 35(5):1232-1244.

[14] THOMSON L I, OSINSKI G R, POLLARD W H. Application of the Brewster angle to quantify the dielectric properties of ground ice formations[J]. Journal of applied geophysics, 2013, 99(99):12-17.

[15] 隋栋训, 童创明, 彭鹏，等. 超低空目标的广义布儒斯特效应[J]. 空军工程大学学报(自然科学版), 2015(4):29-32.

SUI D X, TONG C M, PENG P, et al. Study on G-Brewster of super-low altitude target[J]. Air Force Engineering University Journal(Natural Edition), 2015(4):29-32.(in Chinese)

[16] OBELLEIRO B F, RODRIGUEZ J L, BURKHOLDER R J. An iterative physical optics approach for analyzing the electromagnetic scattering by large open-ended cavities[J]. IEEE transactions on antennas & propagation, 1995, 43(4):356-361.

[17] KAPP D, BROWN G S. A new numerical method for rough-surface scattering calculations[J]. IEEE transactions on antennas & propagation, 1996, 44(5):711.

[18] WEST J C. Analysis of the iterative Kirchhoff approximation for rough surface scattering[C]//IEEE International Symposium Geoscience and Remote Sensing, 1999: 2410-2412.

[19] SARABANDI K, PARK M. A radar cross-section model for power lines at millimeter-wave frequencies[J]. IEEE transactions on antennas & propagation, 2003, 51(9): 2353-2360.

[20] DEHMOLLAIAN M, SARABANDI K. Electromagnetic scattering from foliage camouflaged complex targets[J]. IEEE transactions on geoscience & remote sensing, 2006, 44(10): 2698-2709.

[21] DEHMOLLAIAN M, BIGLARY H. Scattering of an object above a rough surface with impedance boundaries using IPO and FMM[C]//IEEE International Symposium Antennas and Propagation Society, 2012, 1-2.

[22] RASHIDI R E, DEHMOLLAIAN M. Target above random rough surface scattering using a parallelized IPO accelerated by MLFMM[J]. IEEE geoscience & remote sensing letters, 2015, 12(7):1481-1485.

[23] 姬伟杰, 童创明. 二维海面上方金属目标复合散射快速算法研究[J]. 电波科学学报, 2012, 27(2): 307-314.

JI W J, TONG C M. Fast alogorithm of calculating the composite scattering from PEC object above sea surface[J]. Chinese journal of radio science, 2012, 27(2): 307-314.(in Chinese)

Brewster effect from composite rough surface of ground and sea in adjacent region

ZOU Gaoxiang1TONG Chuangming1,2SUN Hualong1WANG Tong1PENG Peng1,3

(1.AirandMissileDefenseCollege,AirForceEngineeringUniversity,Xi’an710051,China;2.StateKeyLaboratoryofMillimeterWaves,SoutheastUniversity,Nanjing210096,China;3.SchoolofPhysicsandOptoelectronicEngineering,XidianUniversity,Xi’an710071,China)

Based on modeling theory of random rough surface, Brewster effect of composite rough surface of adjacent region between ground and sea is studied. The Monte Carlo method is applied to construct composite rough surface. Gauss spectral function is introduced to generate ground rough surface, and Pierson Moskowitz(PM) spectral function is used to simulate actual sea rough surface. Weighted inverse tangent function is presented to filter in order to smooth the borderline between ground and sea. The geometrical model of composite rough surface of adjacent region between ground and sea is established. The couplings of facets in respective region and facets of region near borderline are considered, and an iterative physical optics(IPO) based on facets of composite rough surface of ground and sea in adjacent region is presented. The electromagnetic scattering in the specular direction of composite rough surface of ground and sea in adjacent region is quickly calculated. The influences of root mean square and correlation length of ground rough surface, and wind velocity and wind direction of sea rough surface on Brewster effect are discussed. The “Brewster fusion effect” of composite rough surface of ground and sea in adjacent region is discovered. And the “fusion” phenomenon of Brewster angle is more remarkably affected by root mean square of ground rough surface and wind velocity of sea rough surface. This research provides theoretical basis for detection of actual environment of ground and sea in adjacent region. Numerical results can be used for reference in the field of reducing multipath interference, radar object detection and identification, and remote sensing information processing.

ground and sea in adjacent region; composite rough surface; iterative physical optics; Brewster effect

10.13443/j.cjors.2016112001

2016-11-20

国家自然科学基金(No.61372033)

TN011

A

1005-0388(2016)06-1036-10

邹高翔 (1993-),男,湖南人,空军工程大学博士研究生，主要研究方向为计算电磁学快速算法,军用目标电磁散射特性及战场电磁环境研究．

童创明 (1964-),男,湖北人,国防科技大学和东南大学博士后出站.空军工程大学防空反导学院教授、博士生导师、空军级专家、博士后流动站负责人,国家自然科学基金同行评议,《电波科学学报》编委,主要从事计算电磁学、雷达目标电磁散射特性与目标识别、新型微波材料与应用等领域的教学、科研和学术研究工作.出版学术专著7部、教材3部,发表学术论文400余篇(其中SCI、EI检索230余篇).

孙华龙 (1982-),男,陕西人,空军工程大学博士,主要研究方向为快速电磁计算方法、目标电磁散射特性和环境电磁散射特性．

王童 (1988-),男,河北人,空军工程大学博士,主要研究方向为雷达信号处理、目标电磁散射特性和合成孔径雷达成像．

彭鹏 (1986-),男,陕西人,西安电子科技大学博士,主要研究方向为雷达原理、信号处理和目标电磁散射特性．

邹高翔,童创明,孙华龙,等. 地海交界分区域复合粗糙面的布儒斯特效应研究[J]. 电波科学学报,2016,31(6):1036-1045.

ZOU G X, TONG C M, SUN H L,et al. Brewster effect from composite rough surface of ground and sea in adjacent region[J]. Chinese Journal of Radio Science,2016,31(6):1036-1045.(in Chinese). DOI: 10.13443/j.cjors.2016112001

联系人： 邹高翔 E-mail: gxiangzou@163.com

DOI 10.13443/j.cjors.2016112001