复合铝合金薄壁管在高频感应焊中温度场的模拟

刘小东，王志伟，陈 洪，潘恋恋

（湖北工业大学绿色轻工材料湖北省重点实验室，湖北武汉430068）

复合铝合金薄壁管在高频感应焊中温度场的模拟

刘小东，王志伟，陈 洪，潘恋恋

（湖北工业大学绿色轻工材料湖北省重点实验室，湖北武汉430068）

复合铝合金薄壁管高频感应焊接过程中，焊接温度是影响焊接质量的主要因素。采用有限元分析软件ANSYS模拟其温度场，考虑薄管一次焊透和热计算的边界条件，利用线热源模型加载计算，得出焊接过程的温度分布和热循环曲线，这为进一步分析焊接应力应变提供了相应的理论依据。

薄壁管；有限元；温度场

0 前言

高频焊管是利用高频电流的集肤效应和邻近效应，将待焊管坯的边缘迅速加热到熔融状态，并在挤压辊的作用力下形成焊缝[1]。焊接温度和挤压力是影响焊缝质量的重要工艺参数，而挤压力由一对挤压辊调节控制，相对稳定，故控制焊接温度是保证焊接质量的核心。生产实践表明，焊接温度过高会浪费焊接功率，使待焊边缘部分熔化过多，甚至发生焊缝烧穿现象，影响焊缝的表面质量和焊管的合格率；焊接温度过低则会使待焊处热输入不足，引起冷焊，降低焊管质量[2]。因此分析焊管的温度场及焊缝周围的温度分布十分重要。

目前受技术条件的限制，无法准确实时测量焊管的温度场，而主要依靠经验判断和解析进行计算，随着计算机和有限元技术的发展，数值解法成为当前研究的热点[3-5]。通过有限元软件ANSYS模拟焊管焊接过程的温度场，可以得出任意时刻任意截面的温度分布图，也可以观察其温度的等值面、等值线随时间变化的情况，以及任意点的温度-时间曲线[6]，为实际焊管焊接提供一定的理论依据。

1 高频焊接过程数学模型的建立

1.1 控制方程

高频感应焊焊接过程是高度非线性的瞬态问题，焊接材料的热物理性能随着温度的变化而变化，它的温度场控制方程为

1.2 热源模型

高频焊管焊接是一次焊透，可以把热源看成沿管子厚度的一条线，故采用线热源模型进行热计算，其加热体内部热源强度函数[7]为

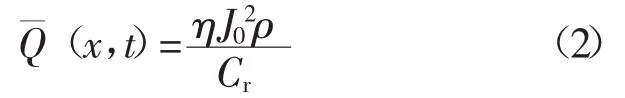
式中Cr为热容量或体积热容[单位：J/（m3·℃）]；ρ为电阻率（单位：Ω·m）；η为效率；J0为表面电流密度（单位：A/m2）[J0=I/Δh0，I为焊接电流；h0为管子厚度（单位：mm）；电流渗透厚度单位：mm）；f为电流频率（单位：Hz）]。

1.3 边界条件

1.3.1对流换热

对流作为面边界条件施加，工件与空气的热对流可用牛顿冷却方程

式中qn为热流密度（单位：W/m2）；h为对流换热系数；TS为工件表面的温度（单位：℃）；TB为周围空气的温度（单位：℃）。

1.3.2辐射

工件表面辐射的影响式为

式中q为边界热流密度（单位：W/m）；σ0为热辐射系数（单位：W·K/m2）；ε为热辐射率（黑度）。由式（4）可知，辐射产生的热流与物体表面绝对温度的四次方成正比，是高度非线性的，容易引起计算的不收敛，因此通过放大高温时的对流系数来间接考虑辐射的影响[8]。

1.3.3相变潜热

焊接过程中熔池区域存在熔化、凝固等相变，伴随相变过程有吸热和放热的能量变化，采用热焓法来考虑潜热，焓值的变化ΔH描述为密度ρ、c比热容以及温度T的函数[9]，存在如下的关系式

2 建立模型和划分网格

以某公司16 mm×2.0 mm×0.3 mm型号的扁平焊管为研究对象，其厚度为0.3 mm，材料为7072/ 3003/4343三层复合铝合金，焊接参数为：焊接电压185 V，焊接电流81.5 A，频率250.4 kHz，焊接速度2 mm/s，焊接热效率0.85。选取高频焊管建立有限元模型，如图1所示，另一半焊管和图示焊管对称，其相应的温度场也对称。为减少划分单元网格总数，重点分析焊缝区域的温度分布，即扁平管焊接部分的区域，可将模型简化为如图2所示的1/4圆筒模型，模型长为100 mm，内圆半径0.7 mm，外圆半径1 mm。

图1 半个焊管模型Fig.1Half of welded pipe model

图2 1/4圆筒简化模型Fig.2A quarter of the cylinder simplified model

选用热分析实体单元SOLID70进行热计算，采用拉伸单元方法，因此还要使用平面热单元PLANE55。热源载荷以热流密度的形式加载在焊管表面上。由于焊管焊缝的热影响区宽度为管坯厚度的1/4～ 1/3[10]，约为0.1 mm，不必要进行细化分网格，故选用网格大小为0.15 mm，网格划分结果放大后如图3所示，划分后得到13 527个节点和8 016个单元。

3 热物性参数的确定

材料的热物性参数主要包括导热系数、比热容、密度、换热系数、线膨胀系数、弹性模量、泊松比等，其中密度ρ随温度变化不明显，其余参数均为温度的函数，呈非线性变化，查文献[11]得到不同温度下热物性参数，并用分段线性拟合法来离散，得到的参数如表1所示。

图3 网格划分模型Fig.3Grid Partition Model

表1 焊接材料的热物性参数和温度的关系Tab.1Relationship between thermal physical property parameters and temperature of welding material

4 温度场的数值模拟及分析

通过ANSYS模拟计算可得出任意时刻的温度分布图，图4～图6分别为焊接过程中0.005 s、0.025 s、0.05 s时的温度场。由图4、图5可知，热源移动速度很快，瞬间形成准稳定温度场。由图5、图6可知，焊接熔池的形状类似为扁圆柱状，与采用的线性热源模型相符合，在热源移动方向被拉成扁平状，在管子厚度方向呈柱状。热源中心温度很高，等温线密集，离热源中心较远处等温线稀疏。

同一圆周线上不同节点的热循环曲线如图7所示，A节点位于焊缝，B节点位于热影响区，C节点与焊缝夹角45°，D节点与焊缝夹角90°。由图7可知，焊缝处的温度最高，达到441℃，热影响区次之，与焊缝距离越远温度越低。焊接时各点的温度先上升后下降，并且升温快降温慢，与焊缝距离越远温度变化速度越慢，最后各点温度趋于参考温度。

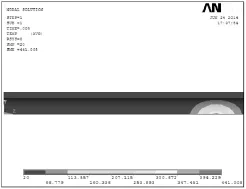
图4 0.005 s时的温度场Fig.4Grid Partition Model

图5 0.025 s时的温度场Fig.50.025 s temperature field

图6 0.05 s时的温度场Fig.60.05 s temperature field

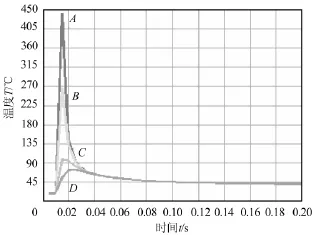
图7 A、B、C、D节点的热循环曲线Fig.7Thermal cycle curves of A、B、C、D node

5 结论

（1）建立高频焊管温度场有限元模型，考虑对流和相变因素，采用线热源模型并以热流密度的形式加载，热源的移动通过加载函数来实现。分析不同时间段的焊管温度分布，发现高频感应焊接过程形成准稳定温度场的时间极短，并且热影响区很窄。

（2）焊接时温度先急剧升高然后缓慢下降，最后趋于参考温度，这个过程中产生的热应力会影响焊接质量，该研究对进一步分析高频焊管的应力应变具有参考价值。

[1]范群波，贵大勇，张淑玲，等.ANSYS 8.0热分析教材和与实例解析[M].北京：中国铁道出版社，2005.

[2]赖明道.直缝焊管机力能参数实验研究[J].东北重型机械学院学报，1982（2）：13-21.

[3]Ko S H，Choi S H，Yoo C D.Effect of surface depression on pool convection and geometry in stationary GTAW[J]. Weld Journal，2001，80（2）：39-45.

[4]Wu Chuansong.Computer simulation of three-dimensional convectionintraveling MIG weld pool[J].Engineering Computations，1992，9（5）：529-537.

[5]HyunJung Kim，SungKie Youn.A Computational Study on the High Frequency Induction Welding Phenomena[A].第一届工程科学与力学中的计算方法国际会议论文集[C]. [C].吉林：2006.

[6]陈洪，刘勇，杨贤镛.森吉米尔中间辊淬火温度场的有限元模拟[J].材料热处理学报，2006，27（4）：126-129.

[7]王海儒，赖明道.高频直缝焊管加热区温度场的一维解析[J].太原重型机械学院学报，1985，6（1）：60-66.

[8]何世权，林建，石玙，等.基于ANSYS有限元对高频焊接的三维温度场模拟[J].兰州理工大学学报，2010，36（5）：27-30.

[9]张朝晖.ANSYS12.0热分析工程应用[M].北京：中国铁道出版社，2010.

[10]史福忠，马建国，陈燕军.ERW焊管焊缝热影响区性状与焊管质量的相关性初探[J].焊管，2007，30（3）：60-62.

[11]谭真.工程合金热物性[M].北京：冶金工业出版社，1994：54-56.

Simulation of temperature field in high frequency induction welding process of composite aluminum alloy thin-walled tube

LIU Xiaodong，WANG Zhiwei，CHEN Hong，PAN Lianlian
（Hubei Provincial Key Laboratory of Green Materials for Light Industry，Hubei University of Technology，Wuhan 430068，China）

Welding temperature is the main factor that influences the welding quality in high frequency induction welding process of composite aluminum alloy thin-walled tube.The finite element analysis software ANSYS was used to simulate the temperature field. One complete penetration of thin-walled tube and boundary conditions of thermal calculation were taken into account.Then a linear thermal model was used to load and calculate to draw the temperature distribution and thermal cycle curves of welding process. Research results provide the corresponding theoretical basis for further analysis of welding stress and strain.

thin-walled tubes；finite element；temperature field

TG456.9

A

1001－2303（2016）06－0085-04

10.7512/j.issn.1001-2303.2016.06.17

2016-02-12；

2016-03-20

刘小东（1989—），男，湖北随州人，硕士，主要从事焊接数值模拟方面的研究工作。