基于应变的路基工作区深度及其影响因素分析*

周正峰　苗禄伟　孙　超

(西南交通大学土木工程学院1)　成都　610031)　(西南交通大学道路工程四川省重点实验室2)　成都　610031)

(西南交通大学高速铁路线路工程教育部重点实验室3)　成都　610031)



基于应变的路基工作区深度及其影响因素分析*

周正峰1,2,3)苗禄伟1,2,3)孙超1,2,3)

(西南交通大学土木工程学院1)成都610031)(西南交通大学道路工程四川省重点实验室2)成都610031)

(西南交通大学高速铁路线路工程教育部重点实验室3)成都610031)

摘要：应用有限元软件ABAQUS，建立了一典型柔性沥青路面结构三维有限元模型，通过分析路基应力应变沿深度的分布，提出了基于应变的路基工作区深度判定标准，对比了基于应变和应力的路基工作区深度和相应的永久变形，进一步分析了汽车轴载、路基模量等因素对基于应变的路基工作区深度的影响规律.结果表明，以附加应变与自重应变之比为0.1作为路基工作区深度的判定标准较为合理；在相同的作用荷载下，基于应变标准的路基工作区深度比基于应力标准的工作区深度大0.21～0.35 m，相应的永久变形大0.14～0.28 mm；在作用荷载相同时，路基工作区深度随路基模量的增加而增大；在路基模量相同时，超载时路基工作区深度具有较大幅度增加，同时，多轴荷载作用的叠加效应对路基工作区深度也有显著影响.

关键词：道路工程；路基；有限元分析；工作区深度；永久变形；应变

周正峰(1981- )：男，博士，副教授，主要研究领域为道路与机场工程

*国家自然科学基金项目(批准号：51008255)、交运输部科技项目(批准号：2011318493720通)资助

0引言

路基永久变形是行车荷载重复作用下路基土塑性变形的累积[1]，路基永久变形不仅直接控制着柔性路面的车辙深度，而且还易导致路面开裂等病害的产生[2].路基永久变形主要发生在路基上部受行车荷载附加应力作用的工作区深度范围内，因此，在计算路基永久变形时，准确判定路基工作区深度就显得尤为重要.目前，路基工作区深度的判定方法有很多，应用最广泛的是基于应力标准的判定方法[3-9]，具体有2种：(1)以某一深度处的荷载附加应力与自重应力之比小于某一值为标准；(2)以某一深度处的荷载附加应力与路基顶面处的附加应力之比小于某一值为标准.

然而，国内外提出的公路路基永久变形预估方法多是基于应变的回归模型，如国际上应用最为广泛的AASHTO 2002模型[10]，以及常用的Tseng-Lytton模型[11]和国内郭忠印等[12-15]提出的预估模型.这些模型首先是确定路基工作区深度，其次是按一定厚度对工作区深度分层，然后根据路基土室内试验结果，通过回归分析，建立路基土塑性应变与所受弹性应变和材料参数之间的关系，从而得到路基永久变形.

这些路基永久变形预估方法在第一步确定路基工作区深度时，往往都采用的是基于应力的判定标准，而在后续计算路基土永久变形时，又采用的是基于应变的预估模型，两者所用的计算参数并不协调统一，影响路基工作区深度判定和永久变形预估的准确性.

鉴于此，文中运用有限元软件ABAQUS，建立一典型柔性沥青路面结构有限元模型，应用该模型，分析应力应变沿路基深度的变化，提出基于应变的路基工作区深度判定标准，对比基于应变和应力标准的路基工作区深度和相应的永久变形，进一步分析荷载、路基模量等因素对路基工作区深度的影响，研究结果可为路基永久变形预估和路基设计提供参考.

1路面结构有限元模型

1.1路面结构和材料参数

路面结构选取一典型柔性沥青混凝土路面，路面结构与材料参数见表1.为考虑不同路基强度对路基工作区深度的影响，路基模量在30～150 MPa范围内取5个值.

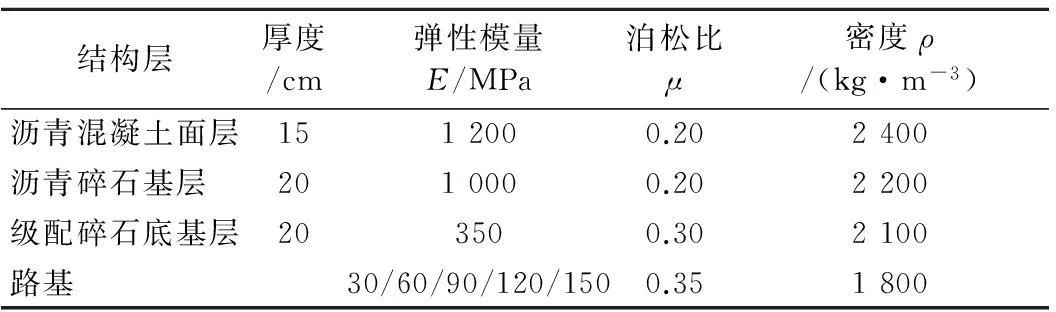
表1　路面结构与材料参数

1.2荷载与模型参数

为考虑不同轴载对路基工作区深度的影响，作用荷载分别考虑单轴双轮(S)、双轴双轮(D)和三轴双轮(T)3种轴型，每根轴的轴重均为100 kN，同时，还以单轴双轮轴重为200 kN作为超载时的工况.轮胎接地面积简化为矩形，其长宽比近似取0.871 2/0.6[16]，荷载参数见表2.模型平面尺寸取6 m×6 m，路基深度取6 m，考虑到结构和荷载的对称性，取1/4模型进行分析，模型中各层材料均采用二次(quadratic)三维实体单元C3D27进行模拟.

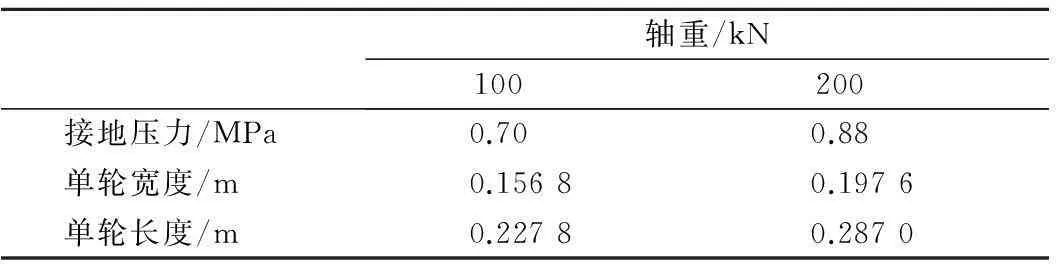
表2　荷载参数

2路基工作区深度判定与对比分析

2.1基于应变的路基工作区深度判定标准

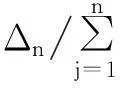
在计算路基永久变形时，采用文献[13]研究提出的预估回归模型.

(1)

lg(ε0/εr)=-8.884 15+0.799 49wc+

8.739 61×10-5Er

(2)

lgρ=-34.404 19+3.364 89wc+

3.357 06×10-4Er

(3)

lgβ=3.996 82-0.393 93wc-

4.580 66×10-5Er

(4)

式中：εp(N)为轮载p重复作用N次时路基土的塑性应变；εv为路基土的弹性应变；wc为路基土的含水量，%；Er为路基土的回弹模量，MPa；ε0,β,ρ为路基土材料参数；εr为测定路基土材料参数时所施加的回弹应变.

路基回弹模量E0取60 MPa，轴载作用次数Ne取重交通等级1 800万次，路基土含水量取12%，分层厚度取15 cm.对比分析基于上述3种标准判定的路基工作区深度，计算结果见表3.

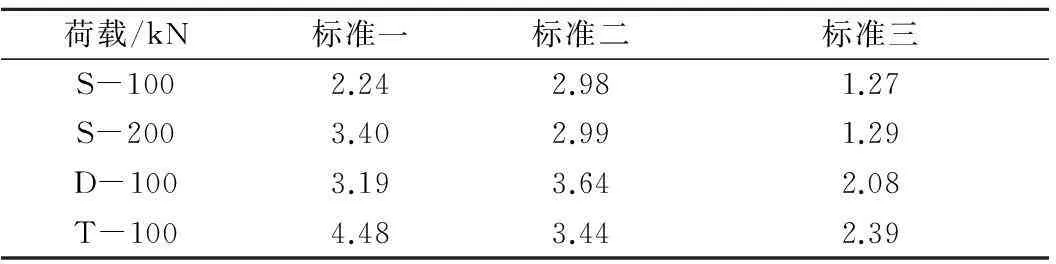
表3　路基工作区深度计算结果　m

由表3可见，与作用标准轴载相比，当为超载时，基于标准二和标准三计算的路基工作区深度几乎没有变化；同时，基于标准二时，双轴要大于三轴作用下的路基工作区深度，这与实际不符.而基于标准一得到的工作区深度则比较合理.因此，在本文分析中，以标准一即εz/εc=0.1作为基于应变的路基工作区深度判定标准.

2.2路基工作区深度和永久变形对比分析

以附加应力与自重应力之比等于0.1即σz/σc=0.1作为基于应力的工作区深度判定标准，以上述提出的附加应变与自重应变之比等于0.1即εz/εc=0.1作为基于应变的工作区深度判定标准，分别计算路基工作区深度；在此基础上，按式(1)～(4)分别计算路基永久变形，对比分析基于应变和应力标准的路基工作区深度及相应的路基永久变形.计算结果见表4.

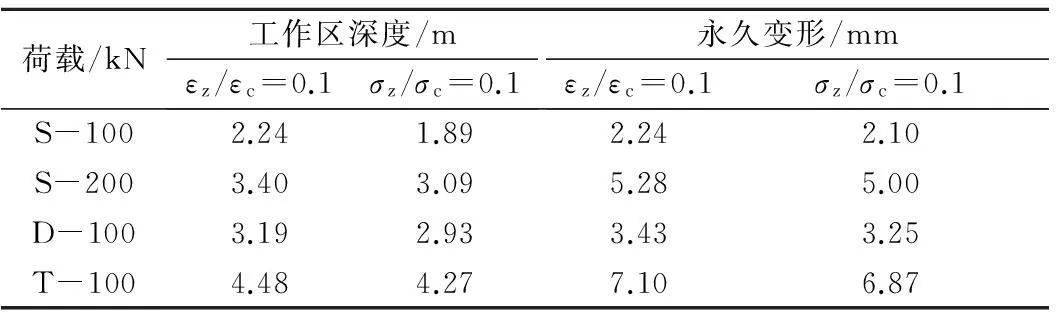
表4　路基工作区深度及相应的永久变形

由表4可见，在相同的作用荷载下，基于应变标准计算出的路基工作区深度和相应的永久变形都要大于基于应力标准计算出的结果.工作区深度的差值在0.21～0.35 m的范围内，随轴数的增加，其差值逐渐减小；相应的永久变形差值在0.14～0.28 mm的范围内.表明应用基于应变的标准来判定路基工作区深度具有一定的必要性.

3路基工作区深度影响因素分析

基于建立的有限元模型，考虑不同荷载和路基模量对路基工作区深度的影响，计算结果见图1、图2.

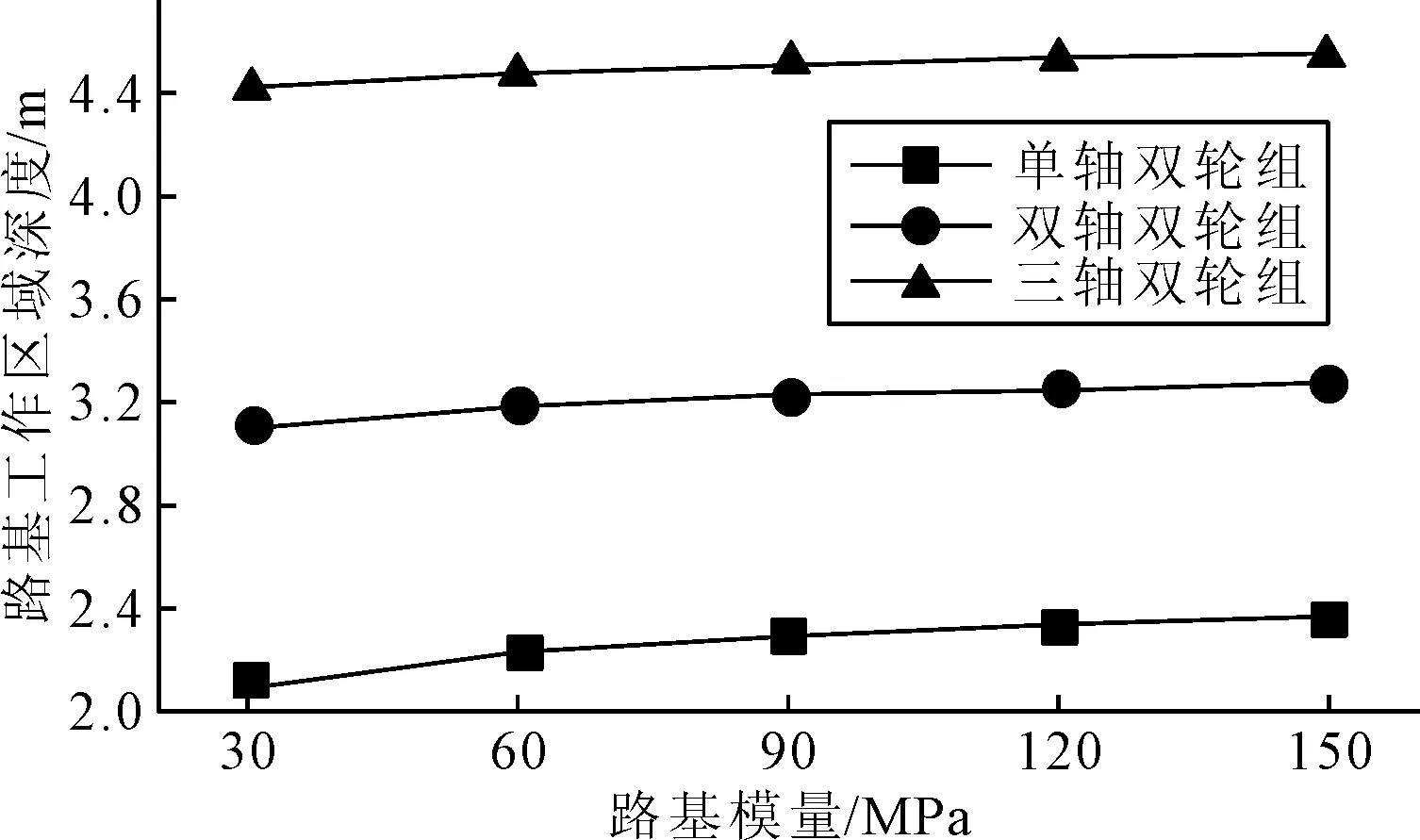
图2　不同轴型作用下路基工作区深度随路基模量的变化

由图1可见，在同一轴重作用下，路基工作区深度随路基模量的增加而增大，但其增大幅度逐渐放缓，以标准轴载为例，当路基模量由30 MPa增大到150 MPa时，路基工作区深度增大了12.5%；当路基模量相同时，与标准轴载作用相比，超载时的路基工作区深度具有较大幅度的增加，两者差值在1.14～1.18 m的范围内，增幅为48.1%～56.3%.

由图2可见，无论在哪种轴型作用下，路基工作区深度均随路基模量的增加而增大，但增长较为缓慢；当路基模量相同时，不同轴型的多轮荷载作用叠加效应显著，三轴作用时的路基工作区深度最大，双轴次之，单轴最小.以路基模量等于60 MPa为例，与单轴作用相比，双轴和三轴作用时的路基工作区深度分别增大了42.7%和100.3%.

以上分析说明，轴重、轴型和路基模量对路基工作区深度均具有较大的影响，尤其是轴重和轴型的影响更为显著，在路基设计中应予以重视.

4结论

1) 通过3种基于应变判定标准的对比分析，确定以附加应变与路基自重应变之比为0.1作为路基工作区深度的判定标准.

2) 在相同的作用荷载下，基于应变标准计算出的路基工作区深度和相应的永久变形都要大于基于应力标准计算出的结果，工作区深度的差值在0.21～0.35 m的范围内，永久变形差值在0.14～0.28 mm的范围内.

3) 轴重、轴型和路基模量对路基工作区深度均具有较大的影响.在同一轴重作用下，路基工作区深度随路基模量的增加而增大；当路基模量相同时，超载时的路基工作区深度具有较大幅度的增加，多轴荷载作用的叠加效应对路基工作区深度影响显著，三轴作用时最大，双轴次之，单轴最小.

参 考 文 献

[1]丛林,郭忠印,高启聚,等.重复荷载下粉性路基土永久变形特性和预估模型[J].公路交通科技,2010,27(4):12-15.

[2]邱延峻,孙振堂.柔性路面路基土的永久变形[J].西南交通大学学报,2000,35(2):116-120.

[3]黎冰,高玉峰,魏代现,等.车辆荷载的影响深度及其影响深度的研究[J].岩土力学,2005,26(S):310-313.

[4]卢正,王长柏,付建军,等.交通荷载作用下公路路基工作区深度研究[J].岩土力学,2013,34(2):316-321.

[5]张军,申俊敏,甘甜,等. 重交通荷载作用下港区地基工作区深度研究[J].岩石力学与工程学报,2014,33(S):2942-2949.

[6]朱海波,贾朝霞,张宏博,等.重载交通下的路基工作区界定问题探讨[J].公路交通科技,2009,26(1):39-44.

[7]李洪亮,王晓华,沈可.天津滨海新区重载交通工作区深度的分析[J].土木工程学报,2011,44(S):158-161.

[8]童申家,蔡佳佳,辛强.考虑铺面结构下的路基工作区深度研究[J].公路, 2012(10):24-27.

[9]郁晓军,隆海健.路基工作区的影响因素研究[J].公路,2012(9):33-36.

[10]NCHRP.Guide for mechanistic-empirical design of new and rehabilitated pavement structures，1-37A [R]. NCHRP，Final Report，2004.

[11]TSENG K H，LYTTON R L. Prediction of permanent deformation in flexible pavement materials[C]. Implication of Aggregates in the Design, Construction, and Performance of Flexible Pavements, ASTM STP 1016, ASTM, Philadephia, 1989,PA:154-172.

[12]同济大学.路基与粒料层抗永久变形性能预估[R].上海：同济大学，2007.

[13]高启聚,郭忠印,丛林，等.重复荷载作用下粘性路基土的永久变形预估[J].同济大学学报:自然科学版,2008,36(11):1521-1525.

[14]张洪亮,郭忠印，高启聚，等.重复荷载作用下砂土永久变形预估模型[J].交通运输工程学报,2008,8(3):58-62.

[15]李冬雪,凌建明，钱劲松，等.黏质路基土永久变形改进计算方法[J].同济大学学报：自然科学版,2013,41(3):386-389.

[16]黄仰贤.路面分析与设计[M].余定选，齐诚，译.北京:人民交通出版社,1998.

Analysis of Subgrade Influence Depth and

Its Influencing Factors Based on Strain

ZHOU Zhengfeng1,2,3)MIAO Luwei1,2,3)SUN Chao1,2,3)

(CollegeofCivilEngineering，SouthwestJiaotongUniversity，Chengdu610031，China)1)

(HighwayEngineeringKeyLaboratoryofSichuanProvince，

SouthwestJiaotongUniversity，Chengdu610031，China)2)

(MOEKeyLaboratoryofHigh-speedRailwayEngineering，

SouthwestJiaotongUniversity，Chengdu610031，China)3)

Abstract：A 3D finite element model for a typical flexible asphalt pavement was established using ABAQUS. By analyzing the stress and strain distribution along the subgrade depth, a new judgment standard for the determination of subgrade influence depth based on strain index was presented, and the comparisons of the subgrade influence depths and the corresponding subgrade permanent deformations based on strain index and stress index were addressed as well. Furthermore, the effect of loading, subgrade modulus on the subgrade influence depths based on strain index were analyzed. The results indicate that it is reasonable to apply the ratio of additional strain to weight strain as the judgment standard for the determination of the subgrade influence depth when the value of the ratio reaches 0.1; Under the same loading, the subgrade influence depths based on strain judgment standards are 0.21～0.35 m more than those based on stress judgment standards, and the corresponding subgrade permanent deformations are 0.14～0.28 mm more and the subgrade influence depths increase with subgrade modulus. In the same subgrade module, the subgrade influence depths increase considerably under overloading, and the multiple load configurations also have a significant impact on the subgrade influence depths.

Key words：road engineering; subgrade; finite element analysis; influence depth; permanent deformation; strain

收稿日期：2015-11-03

doi:10.3963/j.issn.2095-3844.2016.01.009

中图法分类号：U416.1