基于Pro/E双圆弧齿轮参数化建模及虚拟装配仿真

冀　斌，王春燕，卢丽娟，孙天华

(太原科技大学 机械工程学院，太原 030024)



基于Pro/E双圆弧齿轮参数化建模及虚拟装配仿真

冀斌，王春燕，卢丽娟，孙天华

(太原科技大学 机械工程学院，太原 030024)

摘要：将GB/T12759-1991型双圆弧圆柱齿轮作为分析目标，利用软件Pro/E能够进行参数化建模的优点，从而能够快速建立精确的双圆弧齿轮三维实体模型，这样建模可改善设计效率、减少人们的劳动强度，对快速设计我们想要的齿轮具有重要意义，然后对双圆弧齿轮传动机构进行完整约束的虚拟装配，为双圆弧齿轮运动学分析、ANSYS分析以及虚拟制造等后面的课题研究建立了基本条件。

关键词：Pro/E；双圆弧齿轮；参数化建模；虚拟装配；仿真运动

双圆弧齿轮传动本身具有的一些特点，是其它齿轮传动不能与之相比的，从而加快了其在国内外的发展速度。双圆弧齿轮是凸齿廓与凹齿廓之间的啮合，具有接触强度高、跑合性能好、润滑性能好、加工方便、抗胶合能力强、承载能力高、使用寿命长、传动效率高及无最少齿根切限制等优点，在许多行业的好多机械装备上，比如电力、石油、建筑、矿山、化工、冶金、煤炭等，都有大量的应用双圆弧齿轮[1]。本文将GB/T12759-1991型双圆弧圆柱齿轮作为分析目标，分析软件为Pro/E 5.0，利用Pro/E能够进行参数化建模的优点，对于双圆弧齿轮的参数化设计的实现就变得很方便，我们可以通过改变齿轮基本参数就能得到想要的双圆弧齿轮，这样建模可改善设计效率、减少人们的劳动强度[2]。并对双圆弧齿轮传动系统进行虚拟装配，精确建立的参数化三维模型，为双圆弧齿轮机构动态仿真、干涉检验、直观分析、优化设计、有限元分析以及虚拟制造等后续设计开发奠定了基础。

1双圆弧齿轮三维实体建模的建立

双圆弧齿轮的主要参数，像法向齿数z、模数m、螺旋角β、压力角α和齿宽b，决定了其几何尺寸，图1所示为91型双圆弧齿轮的标准齿廓。

1.1　设置齿轮基本参数

进行齿轮的三维模型建立前，我们需要利用Pro/E参数命令对双圆弧齿轮的主要参数进行设置，图2所示为双圆弧齿轮的法面模数、齿数、压力角、螺旋角和齿宽。

1.2　建立计算齿轮每个尺寸的关系式

将齿轮每个尺寸的关系式添加到Pro/E关系对话框中：

ha=0.9m，hf=1.1m，d=mz/cosβ，da=d+2ha，df=d-hf2

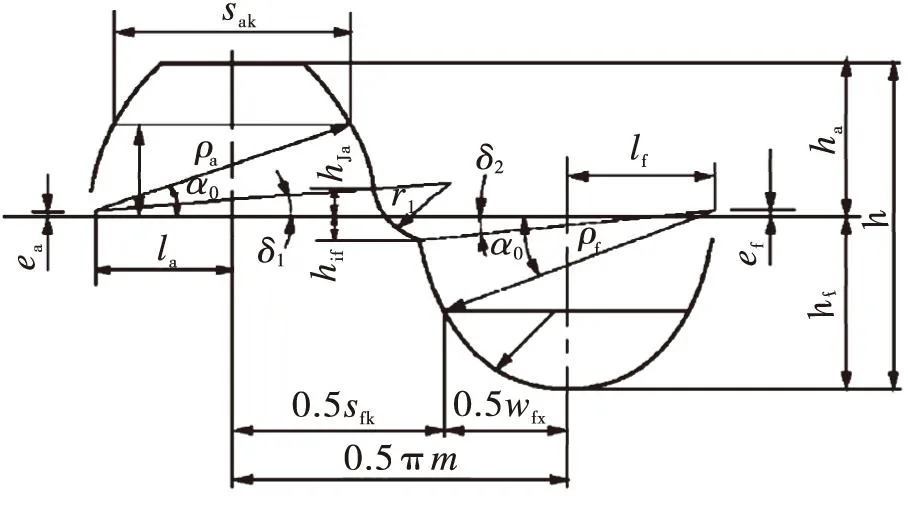
图1　双圆弧齿轮的标准齿廓

1.3　创建基本曲线和螺旋线

根据Pro/E草绘命令进行双圆弧齿轮基本曲线的建立：齿顶圆、分度圆和齿根圆，然后1利用拉伸命令绘制齿坯，拉伸齿根圆，生成圆柱体齿轮齿坯。

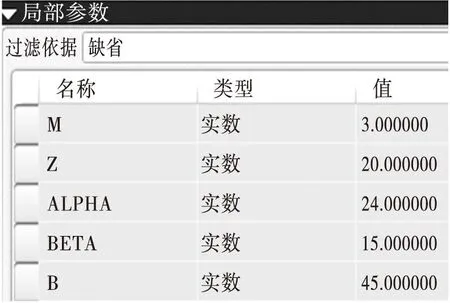
图2　双圆弧齿轮主要参数的设定

根据Pro/E中曲线/从方程/完成命令进行双圆弧齿轮螺旋线的建立，将下面的螺旋线方程输入到系统出现的记事本中：

x=d/2*cos(t*2*b*tan(β)*180/(d*pi))

y=d/2*sin(t*2*b*tan(β)*180/(d*pi))

z=tb

其中d为分度圆直径；b为齿宽；β为螺旋角；β呈正的时候为右旋，反之则为左旋。

1.4　草绘双圆弧齿轮的标准齿形轮廓

根据图1所示的法面标准齿廓曲线，先根据参数关系式绘制出齿轮节线上的标准齿廓，接下来利用几何法将标准齿廓转换到节圆上[3]。先草绘得到双圆弧齿轮的其中一半的齿型轮廓曲线，其次根据镜像命令得到如图3所示的一个完整的端面齿型轮廓，最后利用编辑/特征操作命令沿螺旋线方向复制完成另一端的齿型轮廓，如图4所示。

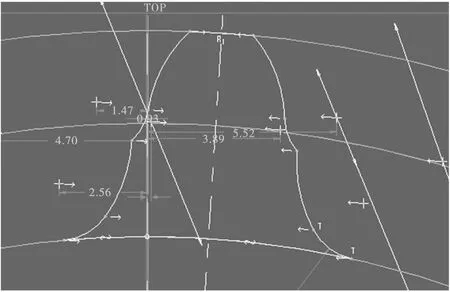
图3　双圆弧齿轮完整端面齿型轮廓

1.5　齿轮实体模型的建立

根据混合扫描命令，沿螺旋线方向将端面标准齿廓进行混合扫描，便会得到图5所示完整的一个齿型。然后利用阵列命令将生成的单个齿型以圆周方式进行阵列，最后进行齿轮孔的拉伸切除，这样便得到了如图6所示的完整的双圆弧齿轮三维实体模型。

图4　双圆弧齿轮基本曲线和螺旋线

图5　双圆弧齿轮单个齿型

图6　双圆弧齿轮完整模型

1.6　参数化设计程序

要想完成参数化设计，必须利用软件Pro/E的编辑和执行程序功能，再将齿轮建模时涉及的参数和关系式结合，参数化各个尺寸，然后添加到RELATIONS。将建立好的齿轮主要参数关系式输入到程序INPUT和ENDINPUT中，例如：Z NUMBER “输入齿数z：”等，然后把齿轮的几何参数关系式再输入到程序RELATIONS和END RELATIONS中。保存好之后，将记事本关闭，这样只需经过简单的输入双圆弧齿轮基本参数，从而便可得到我们想要的任意双圆弧齿轮，参数化设计建模对后面的分析研究具有重要性[4-5]。

2举例对双圆弧齿轮进行装配干涉检测

根据参数化建好的模型，点击再生命令、输入参数，然后输入新的齿数为40，螺旋角为负15°，而模数、齿宽、压力角不变，输入完之后会再生出新的齿轮模型，得到的大齿轮模型如图7所示。首先将图6和图7的一对齿轮以“销钉”方式进行装配，中心距a=(z1+z2)m/(2cosβ)，然后将装配好的一对齿轮进行全局干涉检测，检测结果为无干涉零件，说明建的模型以及装配都没有问题。接下来打开应用程序/机构命令，定义伺服电动机，定义齿轮副，设定小齿轮做驱动后进行模拟运动，如图8所示。最后分析定义，进行全局碰撞检测，检测结果为模拟仿真运动无干涉，可以进行后续的一些分析研究[6-7]。

图7　大双圆弧齿轮模型

图8　一对装配无干涉的双圆弧齿轮

3结束语

双圆弧齿轮造型比较复杂，利用具有强大的参数化与特征建模功能的Pro/E软件，对于实现参数化的双圆弧齿轮设计非常便利。如果在日常的工程应用中，我们只要修改基本参数便可设计得到新的精确的双圆弧齿轮实体模型，这对于改善设计效率和精度具有重要利用价值。以及对于后面的双圆弧齿轮的虚拟装配、干涉检验、模拟仿真、啮合传动分析、优化设计、强度分析以及虚拟制造等研究分析提供了实实在在的齿轮模型，具有非常实用的意义。

我国工业生产者中应用的圆弧齿轮，其圆周速度已超过100 m/s，功率已达20 000 kW，直径4 000 mm以上，模数40 mm，目前研究试制的分阶式双偏圆弧齿轮和硬齿面双圆弧齿轮，已成功地应用于各种减速器和增速器中，并取得了显著的技术经济效果。双圆弧齿轮传动比较平稳，振动、噪声都比较小，双圆弧齿轮对于中心距偏差、切齿深度偏差以及滚刀齿形压力角偏差的敏感性较大，在设计、制造和装配时，同样应予以充分注意。

参考文献：

[1]陈荣增.圆弧齿圆柱齿轮传动[M].北京：高等教育出版社，2002.

[2]康星虎，段建中，闫文斗.圆弧齿轮精确建模的研究[J].煤矿机械，2013，34(3)：63-65.

[3]邓季贤，李进宝，王铁.双圆弧齿轮端面齿廓方程及其啮合过程[J].煤矿机械，2003，24(1)：19-21.

[4]杨晨升，赫会宝.双圆弧齿轮参数化设计研究[J].机械工程师，2010，(10)：58-60.

[5]杨显宏.基于Pro/E双圆弧圆柱齿轮的参数化设计[J].煤矿机械，2012，33(10)：258-259.

[6]张恩光，占向辉，王丽.基于UGNX的2K-H型差动轮系的参数化设计及运动仿真[J].煤矿机械，2012，33(12)：27-29.

[7]孙江宏，黄小龙，高宏.Pro/ENGINEER Wildfire/2001结构分析与运动仿真[M].北京：中国铁道出版社，2004.

Parametric Design of Double Circular Arc Gear Based on Pro/E and Virtual Assembly Simulation Motion

JI Bin，WANG Chun-yan，LU Li-juan，SUN Tian-hua

(School of Mechanical Engineering，Taiyuan University of Technology，Taiyuan 030024，China)

Abstract：GB/T12759-1991 dual circular cylindrical gear as research object， the powerful Pro/E parametric function on precise 3-D parametric solid modeling of double circular arc gear can improve the efficiency and accuracy of double circular arc gear design and virtual assembly， which can provide the basic conditions for double circular arc gear kinematics simulation，ANSYS analysis and subsequent design and development of virtual manufacturing.

Key words：Pro/E，double circular arc gear，parametric modeling，virtual assembly，simulation motion

中图分类号：TH132.4

文献标志码：A

doi：10.3969/j.issn.1673-2057.2016.01.011

文章编号：1673-2057(2016)01-0050-04

作者简介：冀斌(1990-)，男，硕士研究生，主要研究方向为计算机辅助设计及制造。

收稿日期：2015-04-24