预应力下空间站柔性太阳翼动力学特性分析
耿盛韦,王志瑾,胡秋野
(南京航空航天大学 飞行器先进设计技术国防重点学科实验室,南京 210016)
预应力下空间站柔性太阳翼动力学特性分析
耿盛韦,王志瑾,胡秋野
(南京航空航天大学 飞行器先进设计技术国防重点学科实验室,南京 210016)
空间站柔性太阳翼上有以下预应力:1)在轨工作时,会周期性进出地球阴影区,结构温度会发生周期性的变化,温差在结构上产生了热应力;2)中央桁架斜拉杆上作用有展开预应力;3)柔性阵面上施加有张紧力。这些预应力都会引起几何刚度,从而改变太阳翼结构的动力学特性。文章使用Abaqus非线性动力学求解功能,首先对中央桁架部分和柔性阵面部分分别建立有限元模型,研究预应力对太阳翼动力学特性的影响,发现只有柔性阵面上的张紧力影响最为显著;然后针对完整的太阳翼结构,考虑阵面张紧力作用下,研究其动力学特性,并与未考虑预应力引起的刚度变化时的结构动力学特性进行对比分析。
太阳翼;挠性结构;几何刚度;动力学特性;有限元方法
0 引言
空间站在轨运行期间会周期性进出地球阴影区和日照区,使柔性太阳翼各部分经受周期性的温度变化,从而产生热应力;另外,太阳翼的中央桁架斜拉杆上施加有预应力;再者,太阳翼的柔性阵面上施加有维持阵面刚度的张紧力。这些因素都将引起几何刚度,从而改变结构的动力学特性。
由于空间站的型号和数量很少,柔性太阳翼的种类非常有限,在轨使用的也只有几个,有关柔性太阳翼动力学特性研究的文献很少。近年来,随着新一轮航天技术的快速发展,柔性太阳翼结构的动力学特性研究受到了越来越多的关注。Dorsey等[1]通过线性理论分析柔性太阳翼动力学特性,Thornton等[2-3]使用悬臂梁与张力薄膜单元分别建立国际空间站柔性太阳翼与“哈勃”望远镜卷起式太阳翼的连续介质模型,通过弹性体振动理论获得了结构低阶模态的解析解;Carney[4]采用单根悬臂梁等效中央桁架,壳单元作为柔性阵面,利用有限元软件Nastran中非线性求解器SOL105,获得了柔性太阳翼结构前 5阶模态的有限元解;孔祥宏等[5-6]采用梁单元和杆单元建立中央桁架,使用壳单元建立阵面,得到结构的全尺寸有限元模型,分析了结构的动力学特性及在轨热响应特征。
对已有文献进行分析发现,在对太阳翼动力学特性进行研究中,有2点不足:一是计算分析模型过于简单;二是计算分析都以线弹性为前提,未考虑预应力引起的几何刚度。因为考虑预应力时,结构刚度求解是几何非线性的,计算过程需要多次迭代,对于像大型柔性太阳翼这样大尺寸的刚柔混合结构,计算量和难度都非常大,有时迭代还会不收敛,所以多数学者使用线性有限元理论,将几何刚度忽略。
针对以上问题,本文沿用马泽策等[7]使用的详细有限元模型,考虑几何刚度的影响,研究阵面张紧力、桁架热应力以及桁架斜拉杆展开力对柔性太阳翼动力学特性的影响。
1 考虑几何刚度的动力学理论
1.1 应力刚化现象
对于挠性结构,存在大变形、大转角或大应变问题,此时几何方程变为非线性,即在线性方程的基础上增加了二次导数项[8],其张量表示为
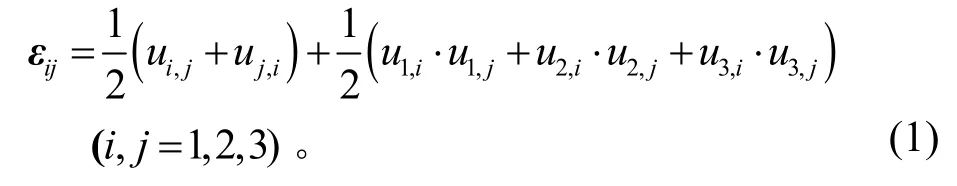
同时,当结构受到预应力时,振动时应力可表示为

其中:σ0为结构预应力;σ1为结构振动过程中产生的应力。利用式(1)与式(2)求解结构的应变能,并略去高阶项,代入哈密顿原理[9-10],得到结构刚度矩阵

式中:KL为刚度矩阵的线性项;KNL为刚度矩阵的非线性项,称为几何刚度。表达分别为:


其中:BL与BNL分别为线性应变向量和非线性应变向量与节点位移向量的转换矩阵,称为几何矩阵,表示为相应微分算子矩阵与形函数矩阵的乘积,具体形式因单元而异;D为材料的本构矩阵,即应力应变关系;S为应力矩阵。

预应力可以是机械载荷,也可以由温度载荷产生。温度引起结构的变形,同时结构变形被约束时,将产生内应力,当温度变化为 ∆T,热膨胀系数为α,对应的应变和应力为:
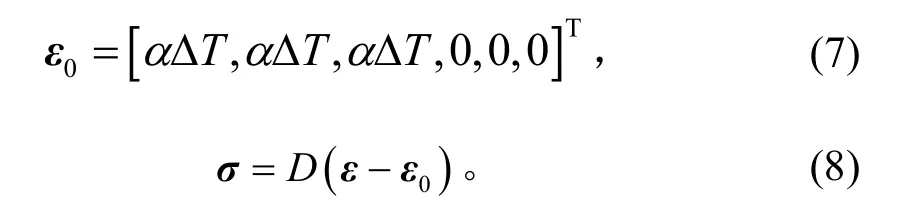
由此发现,考虑几何非线性时,结构上的预应力将引起刚度矩阵的非线性附加项几何刚度,受到拉应力作用时,应力矩阵为正,几何刚度也为正,总体刚度增加;受到压应力则相反,总体刚度减小。这种在考虑几何非线性前提下应力对刚度矩阵的影响,称为应力刚化。
几何刚度的求解需考虑几何非线性,通过前一个平衡迭代的应力状态来计算,至少要迭代2次,计算过程中经常会遇到迭代不收敛,增加了计算难度。
1.2 预应力对动力学特性的影响
动力学求解的基本控制方程为

其中:M为质量阵;C为阻尼阵;K为刚度阵;F为外力阵。
在研究结构的固有动力学特性时,不考虑阻尼项和外力,即C={0},F={0},此时方程(9)变为

该方程的解可以设为x=Xsin(ωt+φ),将其代入式(10),可得

式(11)具有非零解的条件是

求解动力学问题,刚度矩阵一般只有线性项KL,无法描述应力对结构刚度的改变;当考虑几何非线性时,结构内部的预应力场会使刚度矩阵产生非线性附加项(即几何刚度KNL),导致结构刚度发生改变,以此得到的结构固有频率和模态振型也将发生改变,即改变动力学特性。
2 算例分析
商用有限元软件 Abaqus提供了强大的非线性求解功能[11],使用文献[12]中的算例进行验证。根据文献中计算模型,求解绳索在张紧力作用下的动力学特性。绳索截面积1.979 mm2,弹性模量206.84 GPa,密度 7801 kg·m-3,受到的张紧力为2224 N;采用梁单元模拟绳索,划分为20个单元,边界条件取为两端简支,平动自由度释放端作用集中载荷P,有限元模型如图1所示。

图1 张紧绳有限元计算模型Fig.1 Finite element model of the cable under tension
文献[12]中 Thomson使用弦振动解析法求解的张紧绳索前4阶固有频率可认为是精确解。将其与Abaqus数值计算结果进行对比(见表1),从中可以看出计算误差最大仅为 4.1%,在工程允许的误差范围内。由此可以证明Abaqus在求解涉及几何刚度的动力学问题上有较高的准确性。

表1 绳索非线性模态解析解与Abaqus有限元解对比Table 1 Comparison of analytical and numerical solutions of cable’s nonlinear modes
没有张紧力时,绳子的固有频率几乎为0。因此从表1的计算结果还可以看出,张紧力对绳子的动力学特性有很大影响。
3 柔性太阳翼结构
柔性太阳翼主要由刚性中央桁架、柔性阵面、箱体、收藏箱、抬升机构5部分组成,如图2所示,阵面与箱体通过绳索连接,中央桁架两端通过刚性型材与箱体连接,抬升机构末端连接舱体。
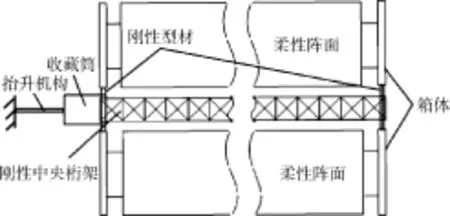
图2 柔性太阳翼结构图Fig.2 Configuration diagram of the flexible solar array
4 中央桁架动力学特性分析
中央桁架结构共有34节,单节结构(如图3所示)由纵杆、横框和斜拉杆组成,展开后斜拉杆上会作用展开力。在有限元建模中,纵杆和横框采用梁单元,斜拉杆采用杆单元,它们的几何和力学参数如表2所示。

图3 刚性中央桁架单节结构Fig.3 One node of rigid central truss
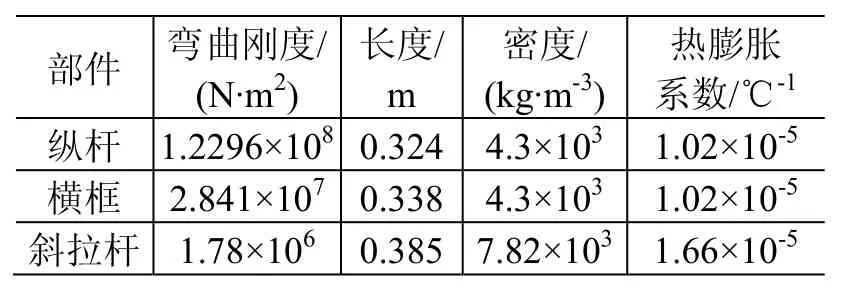
表2 桁架单元性能参数Table 2 Properties of truss
实际结构中,中央桁架两端与阵面收藏箱连接,末端通过抬升机构连接到空间站舱体。阵面与箱体的刚度相对于桁架非常小,可以不考虑其对桁架的约束作用;末端连接的抬升机构与空间站舱体刚度均很大,需考虑它们对桁架末端的约束,因此桁架有限元模型的边界条件为根部固支。在轨飞行过程中,进出地球阴影区会导致桁架的温度发生改变,从而产生热应力;同时,桁架上的斜拉杆在展开后会作用1 MPa展开应力。考虑几何刚度时,热应力和斜拉杆上的展开应力都会影响结构的动力学特性。
在轨飞行期间,桁架上结构的温度场由I-DEAS软件TMG模块解出[13],计算时将桁架温度等效为各节点温度,1个周期内存在最高温与最低温2个极限时刻。从热分析的结果已知,桁架温度不随x轴变化,因此,可以将每一节Oyz平面内的9个点进行编号(如图4所示),并将表3所给出的2个极限状态的温度分别加载,以此求解高温与低温作用下桁架的动力学特性。

图4 桁架节点编号Fig.4 Numbering of truss nodes
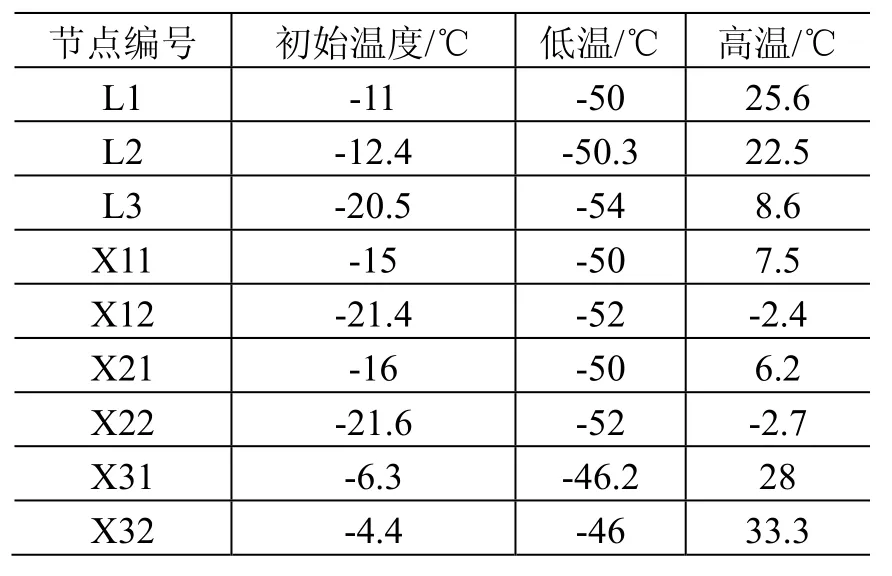
表3 桁架节点温度Table3 Node temperature of the truss
在桁架结构上分别加载低温时刻与高温时刻的温度载荷以及斜拉杆预应力,使用Abaqus计算考虑几何刚度时温度载荷和预应力影响下前10阶模态,将计算结果与不考虑几何刚度的结果进行对比,如表4所示。

表4 中央桁架前10阶模态对比Table 4 Comparison of the first ten modes of the central truss
从表4可以看出,在不考虑温度载荷与预应力时,桁架的模态主要是以二阶弯曲和一阶扭转的形式循环出现,同时由于结构在Oyz平面的对称性,弯曲模态经常以重频形式出现。
将表4中计算结果进行对比,得到如下结论:
1)在考虑几何刚度影响情况下,基本趋势为高温时频率下降,低温时频率上升,主要原因是高温时结构受压,刚度减小,低温时结构受拉,刚度增大;但扭转频率始终都下降,主要原因在于在轨飞行中桁架结构的遮挡作用使结构内部产生不均匀的温度场,造成热应力,使结构产生扭转的趋势,减小了结构的扭转刚度,扭转频率降低。
2)不考虑几何刚度情况下求解会得到重频振型,但在考虑预应力时不再出现重频,原因在于虽然结构几何对称,但温度载荷的非对称使结构刚度不再对称,故重频消失。
3)当考虑斜拉杆展开应力时,解得的频率升高,但这个频率改变比热应力作用下的还要小。
4)虽然考虑几何刚度时频率会发生改变,但从表4可以看出,频率变化量很小,前10阶频率最大变化量仅为 0.1%,而且桁架的振型也未发生改变。主要原因在于在轨阶段温差很小,结构受到的热应力不大,斜拉杆预应力则比热应力还要小得多,同时由于结构本身是刚性结构,KL比KNL大得多,所以温度载荷和斜拉杆展开应力对桁架的动力学特性影响很小。
5 柔性阵面动力学特性分析
柔性阵面通过两侧的绳索与箱体连接,结构如图5所示。阵面以柔性基板为基底,可划分为4个区域,3、4区域贴电池片,1、3区域布置电缆,4个区域材料的力学性能和厚度如表5所示,阵面两侧通过4根绳索与箱体连接,绳索长0.256 m,截面半径0.5 m,杨氏模量210 GPa。密度7800 kg·m-3,单根绳索预紧力50 N。

图5 柔性阵面结构Fig.5 Configuration diagram of the flexible solar blanket
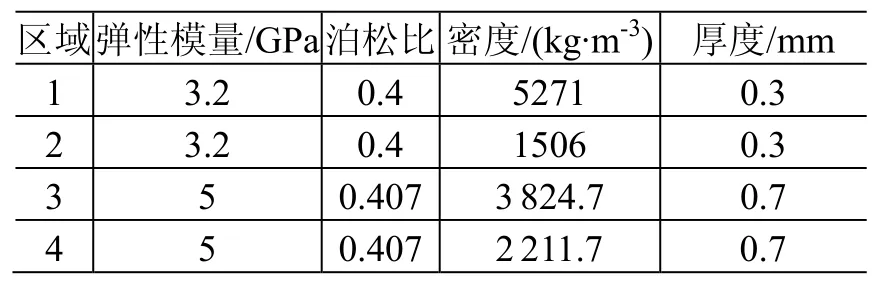
表5 柔性阵面参数Table 5 Properties of the solar blanket
有限元模型中,阵面选用壳单元,绳索选用梁单元,通过MPC(多点约束)beam约束连接绳索与阵面,两侧绳索与箱体连接简化为简支边界条件,并在平动约束释放端作用张紧力。
展开过程中,张紧机构通过绳索施加张紧力,用以维持阵面刚度;同时这套张紧机构可调节绳索的松紧,使张紧力保持不变,从而消除由于温度变化及桁架热变形在阵面上产生的热应力影响。因此,研究阵面的非线性动力学特性时,只考虑张紧力的作用而不考虑阵面自身的热应力。表6为考虑张紧力作用下阵面的前10阶模态与无张紧力作用下模态的对比。

表6 阵面前10阶模态频率对比Table 6 Comparision of solar blankets’ first ten orders of modal frequency
从表6中可以明显看出,考虑张紧力作用时,前10阶频率相比不考虑张紧力作用的线性理论计算结果要高出很多,尤其是第1阶频率增长45倍。同时,阵面的振型也发生了明显的改变。图6给出了一阶弯曲模态与一阶扭转模态的振型对比,可以看出,考虑预紧力时不仅振型发生变化,它们出现的顺序也发生了改变,一阶弯曲模态从第1阶变为第2阶;一阶扭转模态由第3阶变为第1阶。
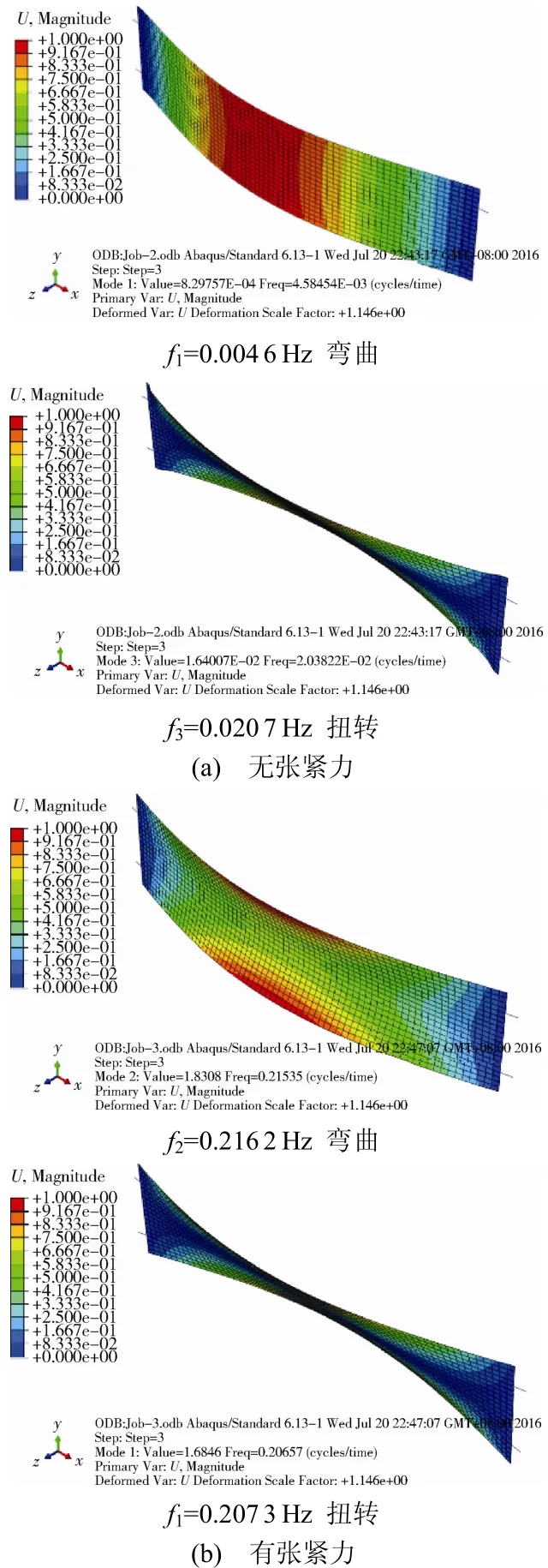
图6 阵面振型对比Fig.6 Comparison of modal shapes of the solar blankets
引起阵面动力学特性发生显著改变的主要原因在于柔性阵面本身材料模量很小;厚度也很小,结构自身的刚度矩阵线性项KL很小,但预紧力所产生的几何刚度项KNL与线性项KL达到了同一量级,显著影响了结构刚度,从而改变结构的动力学特性。
通过对刚性中央桁架和柔性阵面进行单独建模分析,可以发现几何刚度对结构动力学特性的影响不仅取决于预应力的大小,还取决于结构自身的刚度特性。
6 太阳翼全结构动力学特性分析
太阳翼全结构有限元模型如图7所示。箱体采用六面体单元,桁架两端与箱体建立刚体约束,模拟图2所示的刚性型材连接,桁架末端通过集中质量和线刚度模拟收藏箱与抬升机构,抬升机构末端固支,模拟太阳翼与舱体连接。

图7 太阳翼全结构有限元模型Fig.7 Finite element model of the solar array
根据前面的分析,中央桁架上的热应力与斜拉杆展开应力对动力学特性影响很小,阵面上的预紧力影响则很大,因此在分析太阳翼全结构动力学特性时,忽略刚性中央桁架的几何刚度,只考虑阵面上张紧力所产生的影响。
单根绳作用大小为50 N张紧力,模拟太阳翼展开后阵面的张紧状态。前10阶模态结果对比见表7。可以看出在考虑阵面预紧力的作用后,全结构的频率发生了显著提升,第 2阶频率变化最显著,增长到原来的57倍。

表7 太阳翼前10阶模态对比Table 7 Comparison of solar array’s first ten orders of modal frequency
对计算结果进行分析可知,太阳翼的振型可分为3类:第1类为阵面与桁架同时发生弯曲振动,如图8(b)中弯曲模态所示;第2类为桁架与阵面同时发生扭转振动,如图8(b)中扭转振型所示;第3类为仅阵面产生变形,如图8(a)中弯曲振型和扭转振型所示,与文献[2]中的解析计算结果相一致。
虽然第3类振型所占数量最多,但引起结构热诱发振动的本质在于桁架上周期变化的热应力引起桁架的变形,桁架进一步带动柔性阵面产生振动,所以第3类振型在太阳翼结构的动力学特性中并不占主导作用[2]。
对结构的振型做进一步分析可以发现:在不考虑阵面张紧力时,计算结果中均为第3类振型,原因在于此时柔性阵面刚度太小,以至前10阶模态均由阵面激发,与桁架无关;考虑张紧力作用时阵面刚度增加,前10阶模态中存在第1类与第2类振型,因此考虑几何刚度的计算结果更接近真实情况。
7 结论
本文以几何刚度理论为基础,对刚性桁架、柔性阵面和太阳翼全结构分别建模,对其进行结构动力学特性分析,对是否考虑几何刚度的计算结果进行对比,得到以下结论:
1)刚性中央桁架由于自身刚度很大,在轨飞行时中央桁架上温度载荷与展开过程引起的预应力对其动力学特性影响很小,可以忽略。
2)太阳翼阵面自身弹性模量低、厚度小、刚度小,因此当阵面上作用有一定张紧力时,对阵面刚度影响很大,必须考虑张紧力对太阳翼动力学特性的影响。
3)阵面有张紧力作用时,出现中央桁架与阵面一起发生运动的振型。由于结构的振动是由中央桁架所激发,所以此类振型能客观地反映热诱振动本质,考虑几何刚度得到的计算结果符合真实情况。
4)对于柔性太阳翼结构,必须考虑几何刚度对动力学特性的影响。如果有计算成本的限制,可只考虑柔性阵面张紧力产生的几何刚度,忽略刚性中央桁架热应力和展开力对几何刚度的影响。
(References)
[1]DORSEY J T, BUSH H G.Dynamic characteristics of a space station solar wing array[R].Hampton Virginia: NASA Langley Research Center, 1984
[2]THORNTON E A, CHINIT G P, GUILICK D W.Thermally induced vibrations self-shadowed self-blanket solar array[J].Journal of Spacecraft and Rockets, 1995, 32(2): 302-311
[3]THORNTON E A, KIM Y A.Thermally induced bending vibrations of a flexible rolled-up solar array[J].Journal of Spacecraft & Rockets, 1993, 1(4): 2138-2150
[4]CARNEY K.Free-vibration characteristics and correlation of a space station split-blanket solar array[J].AIAA Journal, 1989, 89(1252): 572-583
[5]孔祥宏, 王志瑾.空间站柔性太阳翼桅杆热诱发振动分析[J].上海交通大学学报, 2014, 48(8): 1103-1108 KONG X H, WANG Z J.Thermally induced vibration of the flexible solar wing of mast of space station[J].Journal of Shanghai Jiaotong University, 2014, 48(8): 1103-1108
[6]孔祥宏, 王志瑾.空间站柔性太阳翼热诱发振动分析[J].振动与冲击, 2015, 34(5): 220-227 KONG X H, WANG Z J.Thermally induced vibration analysis of a space station’s flexible solar wing[J].Journal of Vibration and Shock, 2015, 34(5): 220-227
[7]马泽策, 王志瑾, 孔祥宏.柔性太阳翼桅杆涂层特性对热诱发振动的影响分析[J].航天器环境工程, 2016, 33(2): 149-153 MA Z C, WANG Z J, KONG X H.Influence of mast’s coating of the flexible solar wing on thermally induced vibration[J].Spacecraft Environment Engineering, 2016, 33(2): 149-153
[8]王勖成.有限单元法[M].北京: 清华大学出版社, 2003
[9]廖日东, 左正兴, 邹文胜, 等.增压涡轮叶片模态特性研究[J].内燃机学报, 1998, 16(4): 421-429 LIAO R D, ZUO Z X, ZOU W S, et al.The modal characteristic study of turbine blades[J].Transactions of CSICE, 1998, 16(4): 421-429
[10]张年文.几何刚度的推导和应用[J].茂名学院学报, 2004, 14(3): 45-48 ZHANG N W.Derivation and application of stiffness matrix for geometric nonlinear analysis[J].Journal of Maoming College, 2014, 14(3): 45-48
[11]ABAQUS Inc.Abaqus users’ manual: version 6.13[G].2013
[12]THOMSON W T.Vibration theory and applications[M].New Jersey: Prentice Hall, 1965
[13]叶红, 王志瑾.柔性太阳翼在轨热分析[J].飞机设计, 2014, 34(4): 22-26 YE H, WANG Z J.The transient thermal analysis of the flexible solar wing in orbit[J].Aircraft Design, 2014, 34(4): 22-26
(编辑:冯露漪)
Dynamic characteristics of a space station’s flexible solar array with prestress
GENG Shengwei, WANG Zhijin, HU Qiuye
(Ministerial Key Laboratory of Advanced Design Technology of Aircraft, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China)
The flexible solar array (FSA) of a space station has the following kinds of prestresses: (1) the thermal stress caused by periodically varying temperature field in the central truss; (2) the deployment stress in the oblique rod of the central truss; (3) pretension in the flexible solar blanket.These kinds of prestresses will affect the geometric stiffness and change the dynamic characteristics of the FSA.The Abaqus nonlinear dynamic solver is used in this paper.First of all, the central truss and the flexible solar blankets are modeled separately to analyze the effect of the prestress.Results show that the pretension in the flexible solar blanket plays a major role in affecting the dynamic characteristics.Then, the whole model of the FSA is built to analyze its dynamic characteristics in consideration of the pretension.Finally, a comparison is made between the results with and without the prestress.
solar array; flexible structure; geometric stiffness; dynamic characteristics; finite element method
V414.3
:A
:1673-1379(2016)05-0490-07
10.3969/j.issn.1673-1379.2016.05.006
耿盛韦(1992—),男,回族,硕士研究生,主要研究方向为飞行器结构设计;E-mail: gengshengwei@qq.com。指导教师:王志瑾(1963—),女,博士学位,教授,博士生导师,主要从事轻质航空航天结构设计技术等研究。
2016-03-04;
:2016-07-20
江苏高校优势学科建设工程基金资助项目

