基于改进共轭梯度算法的运动模糊图像复原
龚 平
(梧州学院 信息与电子工程学院,广西 梧州 543002)
基于改进共轭梯度算法的运动模糊图像复原
龚 平
(梧州学院 信息与电子工程学院,广西 梧州 543002)
文章在分析运动模糊图像退化原理及建立复原数学模型的基础上,应用共轭梯度法进行图像复原,提出新的βk计算方式和基于改进共轭梯度法的运动模糊复原算法。与经典的FR方法和PRP方法等进行对比实验,实验表明,该文算法复原效果更好,在PSNR评价上平均获得0.3以上的提高。应用于真实拍摄的水平运动模糊图像复原,亦得到良好的复原效果。
共轭梯度法;运动模糊;图像复原
0引言
运动模糊是由于拍照时相机与景物存在相对运动而造成的,是成像过程中普遍存在的问题,对运动模糊图像的复原已成为一个重要课题。传统的复原方法有逆滤波算法、维纳滤波算法、约束最小二乘滤波算法、概率统计算法等等。近年来,随着最优化理论和方法的发展,越来越多的学者将最优化理论应用于图像复原的研究中。
一般的,图像复原过程是一个不适定或病态的反问题[1],可以通过正则化方法进行求解,即引入评价函数对未知数x的可行解进行评价,并期望评价函数的值越小越好。典型的有Tikhonov正则化方法[2]、全变分正则化方法[3]、稀疏约束正则化方法[4]。基于Tikhonov正则化的求解方法中,共轭梯度法具有简单高效的特点,但不同的共轭梯度算法收敛性与数值效果各不相同,带来的复原效果也不同。最经典的共轭梯度法有FR方法、PRP方法、HS方法、DY方法、CD方法等。一般情况下,FR、CD和DY方法有较强的收敛性,HS和PRP方法却有很好的数值实验效果[5]。洪汉玉、陈以超等[6-7]提出的共轭梯度优化的迭代运动模糊图像复原算法,基于经典的FR方法和精确的线性搜索进行迭代计算,算法具有较强的鲁棒性;Zhang等[8]提出基于Tikhonov的迭代共轭梯度正则化(ICGR)方法应用于图像复原,算法可行有效;阎雪飞等[9]提出基于边界条件的预处理共轭梯度运动模糊图像复原算法,有效提高了复原的图像质量。近年来,围绕共轭梯度法中βk的计算及算法的全局收敛性,也有不少的学者从纯数学的角度进行了研究,如文献[10]—[14]等。
本文首先分析了运动模糊图像复原模型,基于Tikhonov正则化方法,将复原问题变换为求解l2范数的最小值问题,再基于共轭梯度算法的基本思想进行求解。针对经典FR方法数值效果和PRP方法收敛性方面的不足,尝试改进共轭梯度法,提出新的βk计算方式并在此基础上提出基于改进共轭梯度法的运动模糊图像复原算法。在同等条件下,与经典的FR方法、PRP方法及其他修正共轭梯度方法进行了对比实验,实验表明,本文的算法具有更好的复原效果,在PSNR客观评价上比其他方法平均获得0.3以上的提高。为了检测本文算法的鲁棒性,对真实拍摄的水平运动模糊图像进行了复原,复原结果令人比较满意。
1运动模糊复原模型
1.1 运动模糊退化过程
设f(x,y)表示原始图像,H(x,y)表示运动模糊的退化模型即点扩散函数PSF,g(x,y)表示观察到的运动模糊图像。考虑加性噪声的情况下,运动模糊的形成过程可表示为:
Hf+n=g
在不考虑噪声的情况下,匀速直线运动模糊的形成过程可表示为:
Hf=g
运动模糊图像复原的目标就是从观察到的模糊图像g设法获得较为清晰的图像f。
1.2运动模糊参数
进行运动模糊复原时必需要知道的两个关键参数分别是运动方向和模糊长度。通过基于运动模糊图像频谱特征的方法或者基于图像微分和自相关函数的方法可以获知运动方向和模糊长度,此外还可以通过基于方向微分算子的方法获知运动方向。
在实际应用中,边界像素条件也至关重要。常用的边界条件有:零边界条件、周期边界条件和反射边界条件(也称Neumann边界条件)。选择不同的边界条件对复原效果有明显的影响。
通过在模糊图像g上施加相应的运算操作得到运动方向、模糊长度的估计值之后,再对边界条件进行假设,从而建立退化模型H。
1.3 复原模型
从g复原f一般是一个病态的反问题。利用Tikhonov正则化策略,变换为求解l2范数的最小值问题:
(1)
令式(1)的导数为0,可得:
HT(g-Hf)+αLTLf=0
(2)
整理得到:
(HTH+αLTL)f=HTg
(3)
设A=HTH+αLTL,则A为正定对称矩阵。同时,设X=f,b=HTg,式(3)则简化成:
AX=b
(4)
求解方程(4)等价于求解最小化泛函J(X):
(5)
通过共轭梯度法对式(5)进行求解,满足误差条件或迭代条件的最优解即为复原的图像。
2共轭梯度复原算法
2.1 经典的共轭梯度算法
共轭梯度法一般采用如下所示的公式计算搜索方向:
(6)
其中gk表示J(Xk)的梯度J(Xk),
所以有 gk=J(Xk)=AXk-b
不同的βk计算方式得到不同的共轭梯度法,经典的FR方法、PRP方法中βk计算公式如下所示:
(7)
(8)
2.2修正的共轭梯度算法
文献[10]提出了一种新的修正的共轭梯度法,在近年来诸多的修正算法中比较有代表性,其在精确搜索步长规则下证明了算法的全局收敛性。该方法具有较好的数值效果和较强的收敛性,其中βk计算公式如下所示:
(9)
上述共轭梯度方法应用于水平运动模糊图像的复原,都能得到评价较好的复原效果,但收敛性和数值效果有较大差异。
3本文改进的共轭梯度算法

图gk-1随迭代次数增加而缓慢趋于0
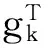
文献[15]利用Gram-Schmidt正交化思想提出一种修正的共轭梯度方法,搜索方向具有充分下降性质且不依赖于线性搜索与βk的选择,其搜索方向计算公式如下:
(10)
本文尝试提出一种新的βk计算公式,如式(11)所示,结合文献[15]的dk,使搜索方向具有充分下降性。在此基础上,提出基于改进共轭梯度法的运动模糊图像复原算法,以期获得更好的运动模糊复原效果。
(11)
βk的计算结果应为标量。对于二维矩阵形式的图像,应用式(11)计算βk时,需要先将gk、dk、gk-1等n*n的矩阵转换成 (nn)*1的向量形式,再参与计算。
本文算法具体描述如下:
STEP1 初始化:取X1=0,β0=0,精度要求ε=1e-7,梯度g1=-b,搜索方向d1=-g,k=1。设置α和最大迭代次数Max,如α=0.0002,Max=10000;
STEP2 通过式(10)计算dk;
STEP3 精确线性搜索计算步长λk。以(nn)*1的向量形式提取n*n的矩阵gk、dk中的数据,计算标量形式的λk:
STEP4 更新X与g:
Xk+1=Xk+λkdk
gk+1=J(Xk+1)=AXk+1-b
STEP5 通过式(11)计算βk;
STEP6 如果‖gk+1‖2≤ε则停止迭代,输出Xk+1;否则k←k+1,如果k 对于水平运动模糊,假设模糊长度已知或通过计算可得。本文选用经典图像Lena、Cameraman进行实验,在MATLAB R2013a中进行了大量的不同模糊长度的运动模糊图像复原仿真实验。在同等条件下,与基于FR的复原方法、基于PRP的复原方法和基于文献[10]的复原方法等进行了对比实验。部分实验结果如图2所示。实验中L选取如下所示的拉普拉斯算子,ω=0.0039。 (a)原图像 (b)运动模糊图像len=50 (c)经典的FR方法 (d)经典的PRP方法 (e)文献[10]的方法 (f) 本文方法 (g)原图像 (h)运动模糊图像len=50 (i)经典的FR方法 (j)经典的PRP方法 (k)文献[10]的方法 (l) 本文方法 采用峰值信噪比(PSNR)评价复原图像质量,该值越大说明图像质量越好。实验结果的PSNR如图3和表1、表2所示。 图3 不同算法的PSNR 表1 Lena图像复原效果的PSNR评价 算法Len=25Len=30Len=35Len=40Len=45Len=50经典FR40.355432.647134.508531.273429.002336.7964经典PRP41.128532.894034.641631.465029.070638.6089文献[10]40.382632.553734.522131.361629.015838.0405本文方法41.215533.170735.142331.668729.675439.2135 表2 Cameraman图像复原效果的PSNR评价 算法Len=25Len=30Len=35Len=40Len=45Len=50经典FR38.021831.708234.381631.218631.319435.8589经典PRP38.768932.079834.538531.531431.358936.4664文献[10]38.060631.781834.397231.356231.329235.8912本文方法38.789232.644534.691531.752931.856236.8352 从表1、表2中可以看出,在不同模糊长度下,本文方法比经典的FR方法、PRP方法、文献[10]方法复原效果的PSNR评价值高。高出的PSNR平均数值如表3所示。 表3 本文方法比其他方法平均高出的PSNR 算法LenaCameraman经典FR0.91710.6768经典PRP0.37960.3043文献[10]0.70160.6256 为了进一步验证本文算法的鲁棒性,对真实拍摄的水平运动模糊图像进行了复原实验。通过基于图像微分和自相关函数的测量方法得到模糊长度的估计值,利用反射边界条件建立退化模型H,考虑到拍摄设备的硬件噪声及真实环境中的不可预知因素,L选择高斯-拉普拉斯算子,如下所示。 复原效果如图4所示。其中,图4(a)得到的模糊长度估计值是21个像素,图4(c)的模糊长度估计值为48个像素。 (a)水平运动模糊的图书封面(b)本文算法复原效果 (c)水平运动模糊的壁画 (d)本文算法复原效果 参数α、ω的取值大小不同会产生不同的复原效果,实验中α、ω选的很小,因此影响了‖gk‖2的收敛速度。此外,L选择单位矩阵或拉普拉斯算子或高斯-拉普拉斯算子,也会因为不同的计算量对算法的运行时间产生影响。 在同等条件下,FR方法、PRP方法、文献[10]的方法以及本文方法应用于水平运动模糊图像复原,最大迭代次数为10000次时,不同算法的‖gk‖2收敛情况如图5所示。 (a)全局收敛情况 (b) ‖gk‖2在[0,1]区间的收敛情况 从图5可以明显看出,本文算法的全局收敛速度比FR方法和文献[10]方法要快,且本文算法总体趋势是收敛的。 本文从βk计算方式的角度对共轭梯度算法进行改进,并应用于水平运动模糊图像的复原。从仿真实验结果可以看出,本文方法复原效果的PSNR评价较好。下一步的优化工作从两方面进行,一是将考虑在不降低PSNR的前提下提升‖gk‖2的下降速度,以期获得更高的算法效率。二是测试更多的真实运动模糊图像,包括不同的模糊长度和运动方向,从实际应用的角度进一步完善本文算法。 [1]Aubert G, Kornprobst P. Mathematical problems in image processing[M]. New York: Springer Science+ Business Media, 2006. [2]A. Bouhamidi, K. Jbilou. Sylvester Tikhonov-regularization methods in image restoration[J]. Journal of Computational and Applied Mathematics. 2007, 206(1): 86-98. [3]A.Beck, M. Teboulle. Fast gradient-based algorithms for constrained total variation denoising and deblurringproblems[J]. IEEE Trans. Image Processing. 2009, 18(11): 2419-2434. [4]洪景新,陈栩. 基于l1正则化的匀速运动模糊图像复原[J].厦门大学学报(自然科学版),2014,53(1):26-30. [5]王安平,陈忠.Wolfe线搜索下一种修正的HS共轭梯度法及其全局收敛性[J].安徽大学学报(自然科学版),2015,39(4):16-19. [6]洪汉玉,陈以超.复杂背景运动模糊图像的盲复原算法研究[J].计算机与数字工程,2006,34(12):7-10+41. [7]陈以超,洪汉玉,张艳.运动模糊图像的去卷积方法研究[J].武汉工程大学学报,2007,29(1):68-70. [8]Jianjun Zhang, Qin Wang. An Iterative Conjugate Gradient Regularization Method for Image Restoration[J]. Journal of Information and Computing Science, 2009, 4(2): 99-106. [9] 阎雪飞,许廷发,白廷柱.改进的预处理共轭梯度图像复原算法[J].北京理工大学学报,2013,33(9):980-990. [10]MohdRivaie, Mustafa Mamat, Leong Wah June, Ismail Modh. A new class for nonlinear conjugate gradient coefficients with global convergence properties[J]. Applied Mathematics and Computation,2012,218:11323-11332. [11]Ibrahim S. M, Mustafa M, Abdelrhaman A, Mohd R, and Zabidin S. A Modified Nonlinear Conjugate Gradient Method for Unconstrained Optimization[J]. Applied Mathematical Sciences,2015,9(54):2671-2682. [12]孙中波,祝英杰,朱振超,等. 一类无约束优化的修正共轭梯度法[J].吉林大学学报(理学版), 2014,52(3):460-464. [13]Chen Y Y, Du S Q. Nonlinear conjugate gradient methods with Wolfe type line search[J]. Abstract and Applied Anlysis,2013(2):1-5. [14]段侠彬,袁功林,王晓亮,等.一种含参数的修正HS共轭梯度法及其收敛性[J].广西大学学报,2015,40(3):751-757. [15]CHENG Wanyou, LIU Qunfeng. Sufficient descent nonlinear conjugate gradient methods with conjugacy condition [J].Number Algor,2010,53:113-131. (责任编辑:覃华巧) Motion Blurred Image Restoration Algorithm Based on Modified Conjugate Gradient Method Gong Ping (School of Information & Electronic Engineering, Wuzhou University, Wuzhou 543002, China) Based on the analysis of the degradation principle and establishment of the math model, this paper applies conjugate gradient method into motion-blurred image restoration and proposes a new method to compute βkand a motion blurred image restoration algorithm based on modified conjugate gradient method. A contrast experiment between the proposed algorithm and the classical FR and PRP has been made and the results show that the proposed algorithm has a better restoration effect, with more than 0.3 PSNR value in average being achieved. When applied to real horizontal motion blurred image restoration, it also provides a good restoration effect. Conjugate gradient; Motion blur; Image restoration 2016-09-30 国家自然科学基金项目(61562074);广西自然科学基金项目(2014GXNSFBB118005);广西高校科学技术项目(YB2014356);广西高校中青年教师基础能力提升项目(KY2016YB438);梧州学院重点项目(2012B004) TP391 A 1673-8535(2016)06-0001-08 龚平(1981-),女,广西灵川人,梧州学院信息与电子工程学院副教授,硕士,主要研究方向:图像处理。4实验结果与分析














5收敛性分析


6结束语

