Mathcad在“自动控制原理”教学中的应用

董德智，王 悦

(铜陵学院 电气与电子工程学院，安徽 铜陵 244000)

Mathcad在“自动控制原理”教学中的应用

董德智，王 悦

(铜陵学院 电气与电子工程学院，安徽 铜陵 244000)

“自动控制原理”课程涉及的数学公式较多，概念相对抽象，学生难以准确把握控制系统的分析方法。本文采用Mathcad进行辅助教学，将复杂的公式图形化。把难以掌握的概念和公式形象地展现在学生面前，提高学生的学习兴趣。

自动控制原理；Mathcad；教学

0 引言

“自动控制原理”是电气工程及相关专业的重要基础课程。该课程内容主要包括控制理论的基本概念与原理、控制系统的分析及其综合设计等。该课程涉及的基础知识涵盖数学、物理学、化学、生物学、系统科学、电工电子、机械基础等，其概念抽象且蕴含较多数学内容，不易掌握[1]。为了使学生熟练掌握该课程，为后续相关专业课程的学习打下坚实的基础，要求在该课程的教学内容上和教学方式上有所更新。

Mathcad作为一款简单易用的数学软件，可以很方便地进行数学运算和图形绘制[2]。其优点是不需编写程序就可以完成复杂的数学运算，具有很强的直观性[3]。其人机界面非常友好，能解决许多复杂的工程计算问题[4]。在课程教学中，我们利用Mathcad的函数计算和强大的绘图功能，详细讲解了“自动控制原理”课程的相关核心知识点，以提升教学效果。

在经典控制理论中，常用时域分析法、根轨迹法和频域分析法来分析控制系统的性能[5]。本文主要阐述Mathcad在上述三种方法在控制系统分析中的应用。

1 在时域分析法中的应用

在控制工程中，二阶系统的应用极为普遍，而且很多高阶系统在一定条件下可以用二阶系统的特征来近似。因此，对二阶系统的全面分析具有实际意义。但是二阶系统的相关参数对其响应的影响比较复杂，初学者很难准确掌握。我们利用Mathcad强大的计算和绘图功能，计算典型二阶系统的单位阶跃响应，并绘制其单位阶跃响应曲线，进而分析系统参数对其影响。

典型的二阶系统传递函数为

(1)

其中：ζ为阻尼比，ωn为自然角频率。

在Mathcad中，阶跃函数为Φ(t)，可以获得输入信号u(t)=Φ(t)的拉氏变换：

进而系统G(s)对输入阶跃响应的拉式变换为

(2)

再用Mathcad的“invlaplace”函数计算C(s)的反拉式变换，从而得到输出的时域响应。

为了分析相关参数对二阶系统阶跃响应的影响，可以先固定一个变量，绘制另一个变量变化时系统的响应曲线。

(1)自然角频率ωn固定，分析阻尼比ζ的影响。

令ωn=10 rad/s，研究阻尼比ζ的变化对二阶系统的单位阶跃响应的影响，响应曲线如图1所示。

图1 ωn固定时，二阶系统单位阶跃响应

从图1可以看出，对于欠阻尼二阶系统(0<ζ<1)，系统单位阶跃响应存在振荡项，且随阻尼比的增大，超调量减小，上升时间变慢，但系统最终会趋于稳定；对于过阻尼二阶系统(ζ<1)，系统单位阶跃响应是非振荡的；对于临界阻尼二阶系统(ζ=1)，系统单位阶跃响应也是非振荡的，且比过阻尼系统更快达到稳定值。

(2)阻尼比ζ固定，分析自然角频率ωn的影响。

分析ζ固定的两种典型情况：欠阻尼(ζ=0.2)和过阻尼(ζ=2)时，自然角频率ωn的变化对二阶系统的单位阶跃响应的影响，响应曲线如图2所示。

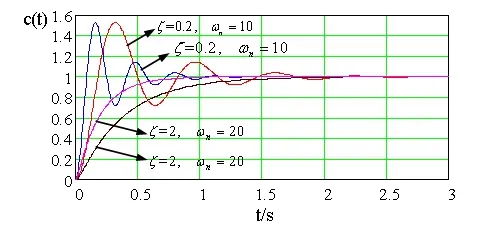
图2 ζ固定时，二阶系统单位阶跃响应

可以看出：只要阻尼比ζ固定，自然角频率ωn越大，系统的响应时间越快。

从上述介绍可以看出，在Mathcad中只要有变量改变，与该变量相关的所有计算结果都会改变，学生通过设置变量的变化，观察系统不同的反应，学习起来更直观，对概念的理解也更深刻。

2 在根轨迹分析法中的应用

根轨迹法是研究闭环系统极点分布与回路增益之间的关系的图解方法，使用简单，在工程实践中得到广泛应用。在根轨迹法的教学中，可辅以Mathcad软件，绘制系统传递函数的根轨迹，进而分析开环增益对系统稳定性的影响。

设开环系统的传递函数G(s)为

(3)

用Mathcad绘制闭环系统根轨迹的方法如下：

(1)计算闭环传递函数的特征多项式H(s)。

H(s)=s4+5s3+8s2+6s+Kp

(4)

(2)利用Mathcad的“polyroots”函数计算闭环传递函数的极点，如下所示。其中sysroots(Kp)表示闭环特征方程的根函数，其变量是开环增益Kp。其中Kp=0对应的是开环传传递函数的极点。

(3)设置Kp的范围，绘制根函数的实部和虚部，得到根轨迹，如图3所示。图中标迹“X”表示开环传递函数的极点。

为了形象地展现开环增益Kp的变化对闭环系统极点的影响，可以用Mathcad的“工具-动画”菜单设置动画。设置方法如图4(a)所示，其中左侧的“FRAME”表示动画的帧数。设置完“终止帧”和“速率”后点击右侧的“动画”，即可生成根轨迹动画文件，图4(b)为动画文件的播放效果。

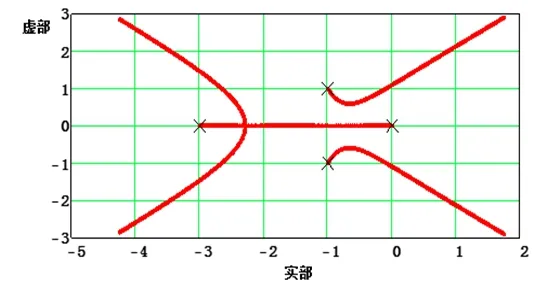
图3 闭环系统根轨迹

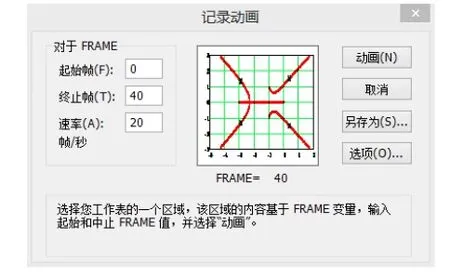
(a)动画设置界面

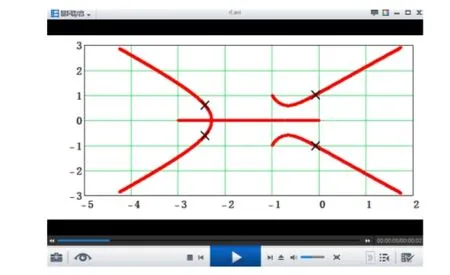
(b)根轨迹动画视频图4 根轨迹视频制作

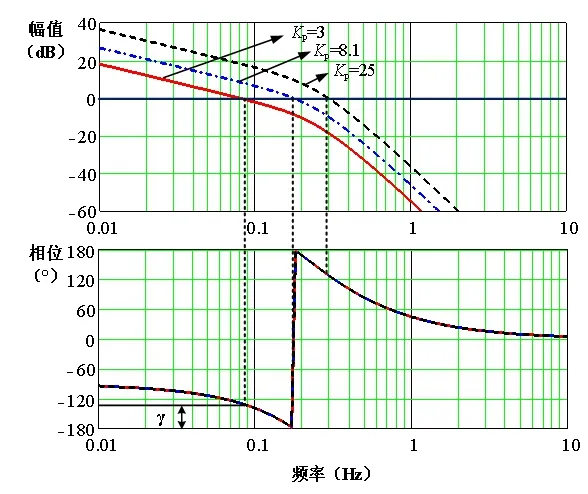
从根轨迹动画视频可以清楚地看到，随着增益的增加，闭环系统的极点会穿过s平面的jω轴，最终到达其右半平面，呈现了系统从稳定到不稳定的整个过程。同时，可以利用Mathcad的跟踪功能，得到根轨迹和jω轴交点的值ω1=±1.1，进而计算Kp=8.1，得到系统稳定时的增益范围为0

3 在频域分析法中的应用

频域分析法是控制系统工程设计的又一基本方法，它和时域分析法互相补充、互相渗透，平行发展，是控制理论中非常重要的内容。本节主要介绍用Mathcad绘制开环系统的对数特性曲线(波特图)，分析对应闭环系统的稳定性问题。以上一节的开环系统式(3)为例，绘制不同增益Kp下的开环系统波特图。

(1)在Mathcad中输入系统传递函数。

(2)用Mathcad的对数函数计算开环系统的幅值。

gain_Gi(f,K):=20·log(|GO(2·i·π·f,k)|)

(3)用Mathcad的相角函数计算开环系统的相位。

(4)分别绘制幅频特性和相频特性曲线。

图5为开环系统波特图，通过修改不同的Kp值，得到不同的特性曲线。可以看出，在Kp<8.1时，闭环系统稳定；Kp>8.1时，闭环系统不稳定；而Kp=8.1时，闭环系统相角为-180°，处于临界稳定状态。

图5 系统波特图

同根轨迹分析法一样，通过用Mathcad绘制开环系统的波特图，可以很直观地看出增益Kp变化对系统稳定性的影响。同时，在系统稳定时，还能方便地看出当Kp=3时，系统的相角裕度γ在45°左右。

4 结语

本文就“自动控制原理”课程的三个重要教学内容，详细说明了Mathcad软件在控制系统分析和可视化教学方面的具体应用。我们引入该软件进行教学后，发现学生对系统分析的兴趣显著提高。同时，学生可以通过自主编程、绘制课程中涉及到的复杂公式曲线，并做相关分析，这些活动大幅增强了他们独立思考和学习的能力。实践表明，该教学方法具有显著的效果。

[1] 胡寿松主编.自动控制原理(第六版) [M].北京:科学出版社, 2013年3月

[2] 白明，方霄，苗俊刚.Mathcad在“微波工程”教学中的应用[J].南京:电气电子教学学报, 2013, 35(6):104-106

[3] 陈昀，郝楠.Mathcad在华工数值方法中的应用[J].北京:计算机与应用化学, 2003, 20(1):71-74

[4] 毛建华，华建文.MATHCAD解决工程问题[J].北京：计算机应用与软件, 2005, 22(12):136-138

[5] Farid Golnaraghi, Benjamin C.Kuo.Automatic Control Systems [M].New York:John Wiley &Sons, Inc, 2010.5

Application of Mathcad in the Teaching of Automatic Control Theory

DONG De-zhi, WANG Yue

(CollegeofElectricalEngineering,TonglingCollege,Tongling244000,China)

Automatic Control Theory course is full of complex mathematical formulas and abstract concepts, It is difficult for students to accurately grasp the way of analyzing control systems.This paper tries to apply Mathcad to assist teaching and transform formulas and concepts involved in the process of the control system analysis to figures.It is convenient to demonstrate the complex concepts and formulas in front of students and the students′ study interests are enhanced finally.

automatic control theory; Mathcad; teaching

2016-01-08;

2016-04-07

董德智(1980-)，男，硕士，讲师，主要从事电力电子变换器设计和控制的教学和研究工作，E-mail：dezhidong@126.com

G434

A

1008-0686(2016)06-0146-04