桩径对Mindlin附加应力系数的影响分析

郭帅杰，宋绪国，许再良，隋孝民，任庆昌

(1.铁道第三勘察设计院集团有限公司，天津　300251；2.轨道交通勘察设计工程实验室，天津　300251；3.西南交通大学，成都　610031)



桩径对Mindlin附加应力系数的影响分析

郭帅杰1，2，3，宋绪国1，2，许再良2，隋孝民1，任庆昌1

(1.铁道第三勘察设计院集团有限公司，天津300251；2.轨道交通勘察设计工程实验室，天津300251；3.西南交通大学，成都610031)

摘要：基于Mindlin理论关于点荷载附加应力系数的解析解答，研究不同土体泊松比、桩长条件下桩径对Mindlin附加应力系数的影响规律，确定不同偏差标准下必须考虑桩径影响的最小范围，并给出需考虑桩径影响最小范围的拟合公式。研究结果表明，土体泊松比Mindlin附加应力系数总体影响较小，统一采用0.35土体泊松比引起附加应力计算偏差一般不超过5%；Midlin附加应力计算中，必须考虑桩径影响的最小范围主要与桩径相关，且随桩长的增加而增大；分别采用1%和5%误差标准时，必须考虑桩径影响的最小范围分别为桩径的13.6倍和6.41倍。

关键词：Mindlin方法；附加应力系数；桩径；桩长；影响范围

海大学，工学博士，E-mail:ggssjj@hhu.edu.cn。

刚性桩复合地基沉降计算主要涉及刚性桩加固区和桩端下卧层附加应力确定问题，相较于假定荷载作用于地基表面的Boussinesq解答，Mindlin方法可以进行任意深度荷载作用下的附加应力计算，因此，Mindlin方法较Boussinesq方法在理论和计算结果的逻辑方面均更为合理[1]。但是，Mindlin方法参数较多，公式极为繁杂，其在工程中的应用经历较长的过程。其中，Geddes将单桩荷载定义为桩端阻力、矩形和线性桩侧阻力3种荷载形式[2]，通过对Mindlin集中应力解析解积分，得到单桩荷载作用下桩周土体任一点附加应力表达式，得到三种荷载形式下的附加应力系数。现有研究结果也表明[3-5]，Geddes-Mindlin解答较Boussinesq解答更符合桩基础承载及沉降变形的实际，前者计算结果更为合理且更为接近工程实测结果。

必须注意的是，桩端阻力和桩侧摩阻力分布范围与桩径直接相关，但现有关于Mindlin方法的研究成果较少涉及桩径对附加应力计算结果的研究，大多将端阻力和桩侧阻力作为作用于桩体中心轴线上的集中荷载进行处理[6-8]。《建筑地基基础设计规范》(GB50007—2002)关于Mindlin附加应力系数的计算同样未考虑桩径影响，但我国《建筑桩基技术规范》(JCG94—2008)通过数值积分方法给出了考虑桩径影响的Mindlin附加应力系数。事实上，Mindlin附加应力计算中关于桩径因素的考虑是存在特定范围的，即附加应力计算点同荷载作用点间距离超过一定限度，桩径对附加应力系数影响将可忽略。由于现有规范关于是否考虑桩径因素的规定尚不统一，故桩径对Mindlin附加应力系数影响规律及考虑桩径影响的最小范围仍需进一步研究总结。

本文基于集中荷载Mindlin应力解析解，通过荷载作用区域点荷载附加应力叠加方法，得到桩周土体任一点位置处总附加应力，进而得到桩径对土层附加应力的影响规律。通过不同土体泊松比、桩长及桩径的Mindlin附加应力系数计算结果对比，由数据拟合方法得到必须考虑桩径影响的最小范围Lmin同桩半径间的关系式，在保证Mindlin附加应力计算精度基础上，避免数值积分方法的反复叠加，大幅提高计算效率，不仅为Mindlin方法在高速铁路、公路等刚性桩复合地基沉降计算中的推广应用奠定基础，也为沉降模型程序算法的实现提供技术支持。

1Mindlin附加应力系数表达式

1.1　集中荷载作用下的Mindlin附加应力

针对地基内部一定深度处作用集中力情况，美国学者Mindlin在1936年关于半无限体内集中力作用下的附加应力分布规律研究中[9]，得到集中荷载Qb作用下，深度z位置处附加应力表达式(1)，图1为直角坐标系下的计算简图。相应地，式(2)为集中荷载附加应力系数。

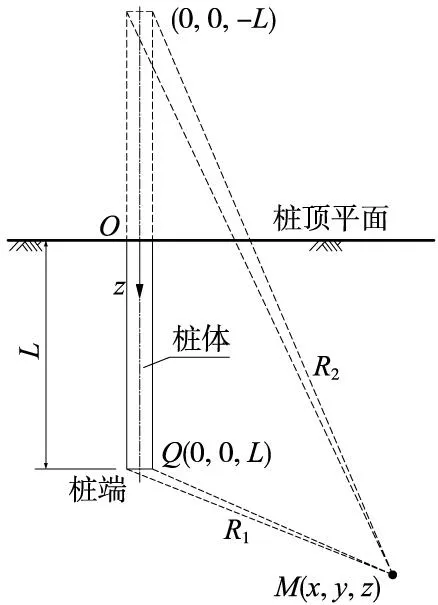
图1　Mindlin附加应力计算简图

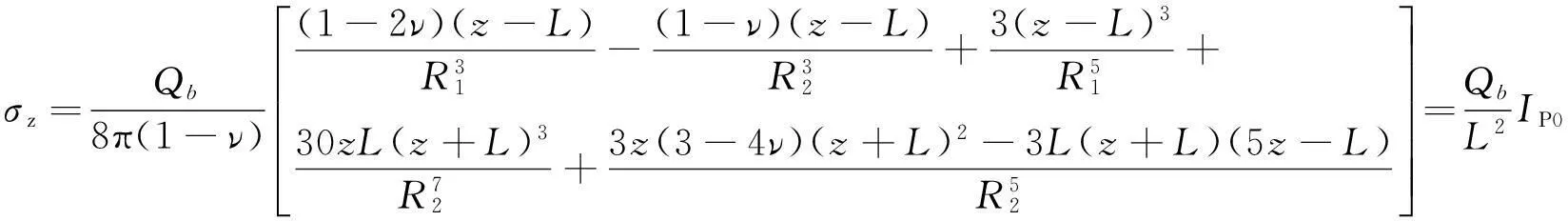
(1)

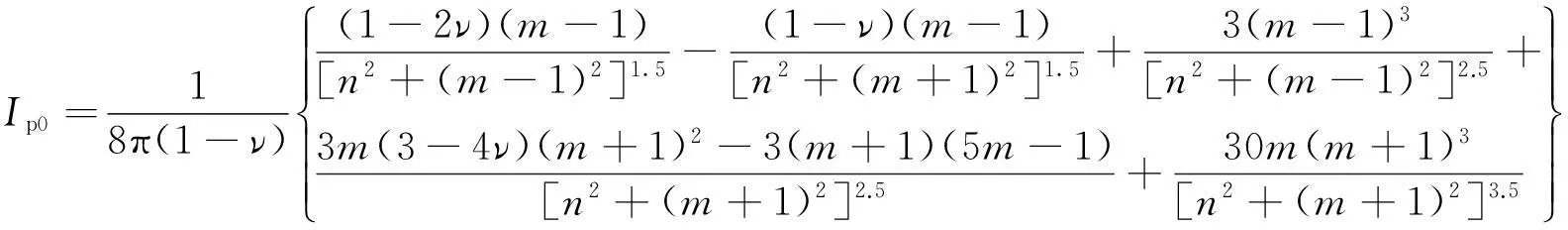
(2)

式中，σz为集中荷载引起的附加应力；Qb为集中荷载；v为泊松比；L为荷载作用点位置坐标，z为计算点深度；m和n为相对于桩长的位置坐标参数，其表达式分别为m=z/L，n=ρ/L；R1为附加应力计算点与集中荷载作用点间距离；R2为附加应力计算点与集中荷载作用点关于z=0平面镜像点间距离。

根据图1中附加应力计算点同集中荷载作用点之间的位置关系，可以得到直角坐标系和径向坐标系下R1、R2表达式

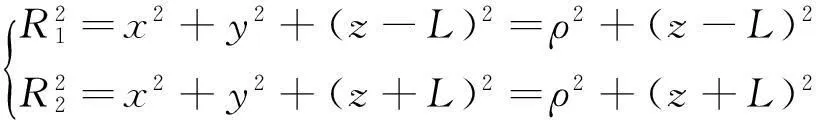
(3)

式中，x、y、ρ分别为附加应力计算点位置坐标和径向坐标。

1.2　考虑桩径影响的Mindlin附加应力系数

不考虑桩径影响时，桩端荷载为集中力，可得到地基中任意一点处附加应力解析解，主要适用于桩径较小或带有桩尖的预制桩。但对于大直径灌注桩或未设桩尖的预应力管桩，应考虑桩径对桩周土体附加应力的影响。假定桩端荷载为圆形均布荷载，由荷载作用面上微面积集中荷载积分方法进行不同位置处附加应力计算，圆形均布荷载微面积积分区域示意如图2所示。对于图2(b)中圆形桩端荷载作用面，得到微面积域dA=rdrdθ范围内集中荷载引起的任意一点附加应力dσz表达式(4)。

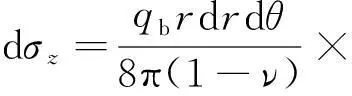
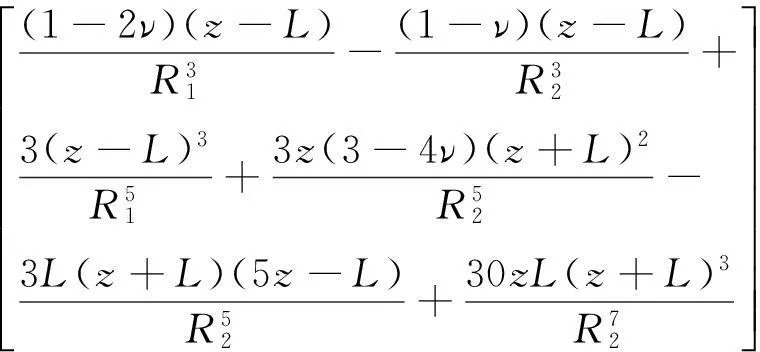
(4)

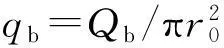
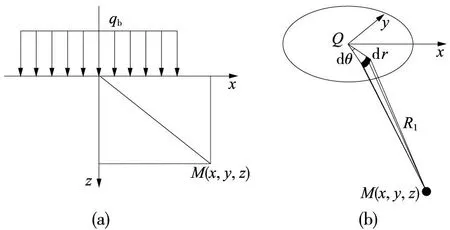
图2　圆形均布荷载附加应力计算简图

对于图2(b)中桩端微面积域内集中力的附加应力计算图示，圆形桩体为中心对称体，当附加应力计算点M与桩体中心线的径向距离相等时，桩端荷载在同一深度圆环区域上的附加应力均相等。因此，可令计算点M纵坐标y=0，x坐标即为M点与桩端轴线间距离ρ，对应的，R1和R2表达式分别为

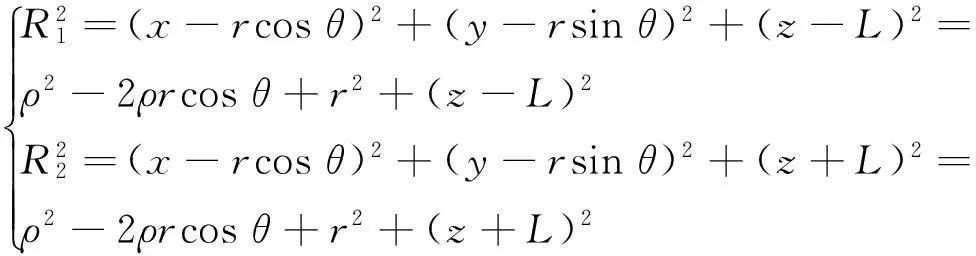
(5)

式(5)代入式(4)，同时令rL=r/L，r0L=r0/L，对附加应力系数表达式(4)进一步简化，得到同式(2)类似的考虑桩径影响的Mindlin附加应力系数表达式(6)。

必须说明的是，式(6)中附加应力系数IP1为关于变量rL的积分函数，难以获得其对应的解析解答；具体计算中，由桩端圆形荷载平面内的逐点积分，继而进行逐点叠加进行求解。

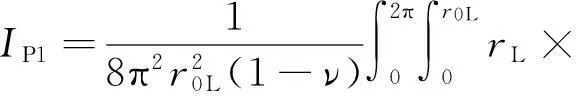
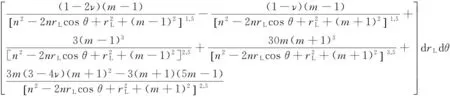
(6)

2桩径对附加应力的影响规律分析

2.1　土体泊松比影响

现有研究结果表明[1]，其他条件完全相同时，Mindlin附加应力随泊松比保持递增关系，但是土体泊松比引起的附加应力计算结果偏差很小，一般不会超过15%。

本文通过对不同泊松比情形下Mlindlin附加应力系数的对比分析，得出如下结论：土体泊松比对Mindlin附加应力系数影响相对较小，统一采用泊松比v=0.35进行Mindlin附加应力系数计算时，极端情况下(v=0.25和v=0.45)出现的误差均不超过10%，一般情况下的误差可控制在5%范围之内，说明在缺少地层物理性质指标或进行桩基沉降量预估计算时，可统一采用泊松比v=0.35进行Mindlin附加应力系数计算。

2.2　桩径引起的附加应力系数偏差

考虑桩径影响时，式(6)采用二次积分方法进行数值求解，分别于弧度方向和半径方向定义100×100网格，采用逐网格叠加方法完成式(6)数值积分计算。此外，式(6)中附加应力系数积分边界r0L为桩半径和桩长的比值，即使桩径完全相同，桩长L的差异也将影响附加应力计算结果。

为对比分析桩径、桩长、土体泊松比对Mindlin附加应力系数计算结果的影响，共进行v=0.25、0.30、0.35、0.40和0.45，桩半径r0=0.15、0.20、0.30、0.40、0.50 m和0.60 m以及桩长L=6、10、15、20、30、50 m共5×6×6=180种情形下的附加应力系数计算。

根据式(6)不同桩径和桩长条件下的Mindlin附加应力系数计算结果，将其与式(2)不考虑桩径影响的解析计算结果进行对比，经式(7)的进一步计算处理，得到不同桩长和泊松比条件下桩径因素引起的Mindlin附加应力系数偏差百分比δ1。

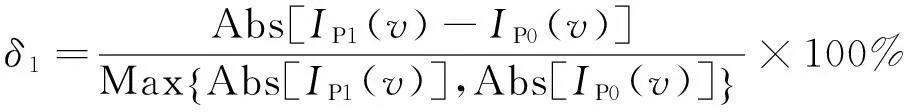
(7)

根据前述180种情形的计算结果，经式(7)处理后，分别得到泊松比v=0.35，桩长L分别为6，15 m和30 m时，0.15、0.30 m和0.60 m桩径情形下，相较于式(2)解析解答，桩径引起的Mindlin附加应力系数偏差分布云图如图3所示。

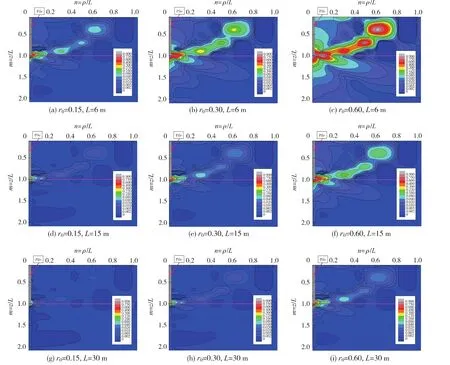
图3　桩径引起的附加应力系数偏差云图

根据图3中不同桩长和桩径条件下的Mindlin附加应力系数偏差分布云图，桩长相同时，相对于式(2)不考虑桩径影响的解析解，式(6)考虑桩径引起附加应力系数偏差幅值及范围均随桩径的增加而增大。同时，桩径相同情况下，考虑桩径引起的偏差百分比δ1数值和分布范围随桩长的增加而减小，即桩长越大，桩径引起的附加应力系数偏差百分比分布范围越小。

必须指出的是，Mindlin附加应力系数公式中桩长L的影响均体现为相对意义，隐含于m、n和r0L参数之中。前述得到的桩径影响结论仅是针对深度比值m和径向坐标比值n意义上的结论，反映在绝对的深度坐标z和径向坐标ρ上，其实际影响区域可能表现出完全相反的变化规律。因此，绝对意义上的桩径、桩长以及泊松比对附加应力系数偏差计算结果的影响仍需要进一步的分析。

3考虑桩径影响的最小范围Lmin

3.1　最小范围确定方法

根据图3中考虑桩径引起的附加应力系数偏差百分比分布云图，以桩端中心为基点，桩端下卧层附加应力计算点与桩端中性点距离越大，相应的偏差百分比越小，当计算点与桩端基点距离超过一定限度后，桩径引起的附加应力系数计算误差将可忽略。因此，可分别设定δ1=1%和5%两种情形的偏差控制标准，以此确定不同控制标准下考虑桩径影响的最小范围Lmin。Lmin确定过程如下：①由建筑物或工程沉降变形控制等级确定相对应的附加应力计算偏差控制标准；②以图3中的桩端中心为基点，确定满足相应偏差标准(如1%、5%等)对应的桩端下卧土层中最远位置处n和m值；③由式(8)确定不同偏差标准下，附加应力计算中必须考虑桩径影响的最小范围Lmin。

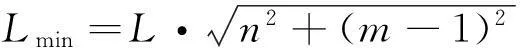
(8)

3.2　最小范围Lmin影响因素分析

根据前述不同土体泊松比、桩径和桩长条件下Mindlin附加应力计算结果，由式(8)确定Mindlin附加应力系数计算中必须考虑桩径影响的最小范围Lmin，继而得到Lmin关于桩径、桩长以及土体泊松比的变化趋势。其中，泊松比v=0.35时，Lmin关于桩径与桩长的变化趋势如图4所示，图5为Lmin关于土体泊松比的变化趋势。

图4(a)中，1%和5%偏差标准对应的考虑桩径影响时的最小范围Lmin均随桩径的增加而增大，其中，1%偏差标准对应的Lmin随桩径变化区间为1.80～7.62 m，最大变化幅度为5.82 m；5%偏差标准对应的Lmin随桩径变化区间为0.67～3.41 m，最大变化幅度为2.74 m，并且1%偏差标准下Lmin数值远大于5%偏差标准。图4(b)中，Lmin随桩长的增加基本保持增加趋势(桩径较大情形)，即桩长越长，需考虑桩径影响的区域范围越大，1%和5%偏差标准对应的Lmin随桩长的最大变化区间分别为6.01～7.02 m(最大变化幅度1.01 m)和2.77～3.41 m(最大变化幅度0.64 m)，此现象并不同于图3中附加应力系数偏差百分比云图。其原因分析如下：图3中考虑桩径影响的区域实为附加应力计算点深度z和径向坐标ρ关于桩长L的比值，虽然云图中的附加应力系数偏差分布区域随桩长的增加而减少，但最小影响范围Lmin随桩长的增加却表现为增加趋势。此外，图4(b)中最小范围随桩长逐渐增大的变化趋势在桩径较大时(r0>0.30 m)表现的更为明显，桩径较小时，则为先增加后减小或逐渐减小的趋势。

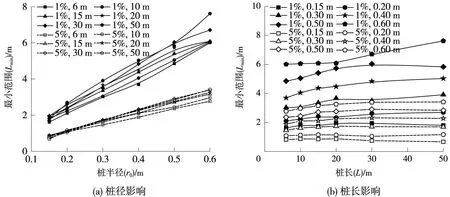
图4　最小范围Lmin关于桩径和桩长的变化趋势

图5为1%和5%偏差标准下，Lmin随土体泊松比v变化趋势，从图中可明显看出，Lmin随土体泊松比v基本保持不变或小幅增加趋势，其增加幅度远小于桩径对Lmin的影响，说明土体泊松比对Lmin相对大小的影响基本可以忽略，此结论与前述土体泊松比对Mindlin附加应力系数影响的研究结果一致。

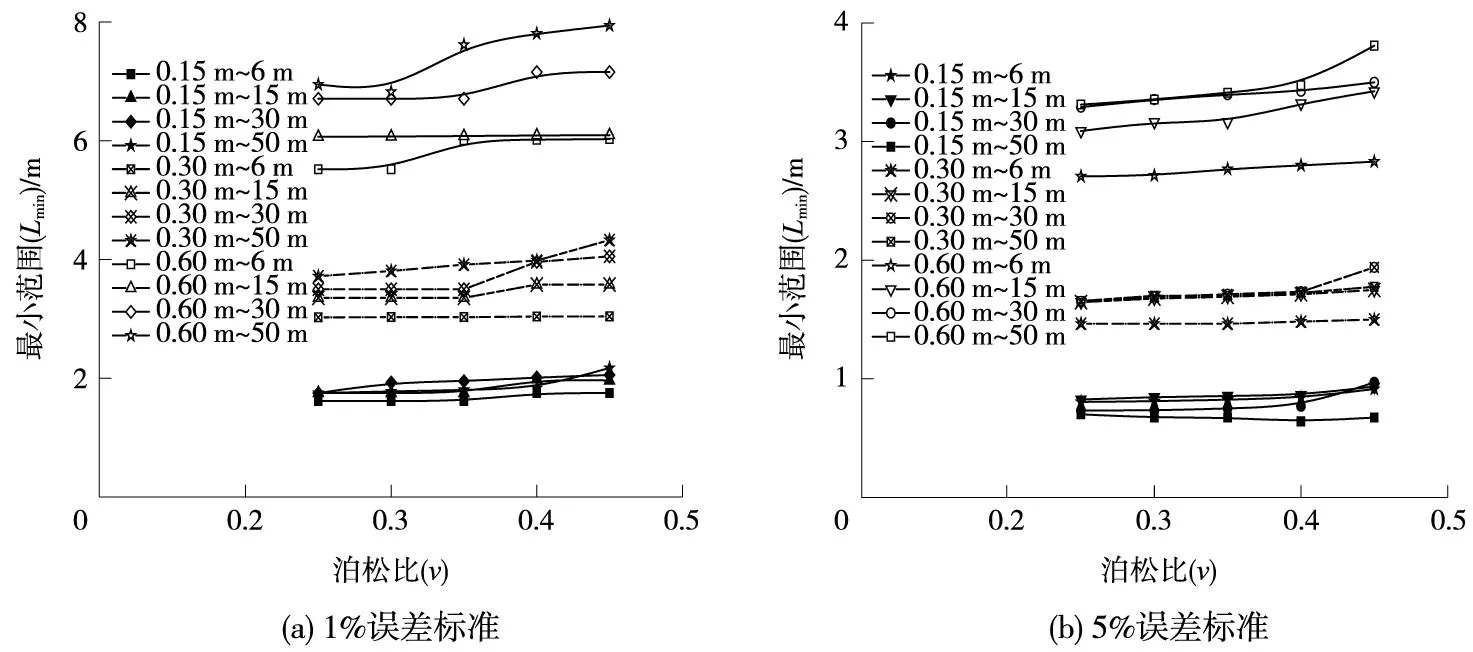
图5　最小范围关于泊松比的变化趋势

综合图4和图5中不同桩径、桩长及土体泊松比对Lmin的影响趋势及其变化区间，可以确定Lmin相对大小主要决定于桩径，而桩长影响次之，土体泊松比引起的桩径影响范围Lmin的变化最小。

3.3　最小范围Lmin拟合公式

基于以上分析，确定桩径、桩长及土体泊松比对Lmin影响趋势后，得到Lmin相对大小的主要决定因素为桩径。忽略桩长和土体泊松比影响，建立起Lmin与主要决定因素桩体半径r0间的拟合关系；拟合关系式中Lmin的取值为桩径相同时，桩长和土体泊松比不同情况下对应的Lmin最大值。

图6为1%和5%附加应力偏差标准下得到的必须考虑桩径影响的最小范围Lmin与桩半径r0间的关系曲线。根据数据点分布特点，采用截距为0的线性拟合方程。1%和5%偏差标准对应的线性拟合曲线方程的斜率分别为13.6和6.41，即当附加应力计算点和桩端荷载作用点距离分别大于13.6r0和6.41r0时，即可不考虑桩径对Mindlin附加应力系数的影响，可直接采用集中力作用下的解析式(2)进行计算。

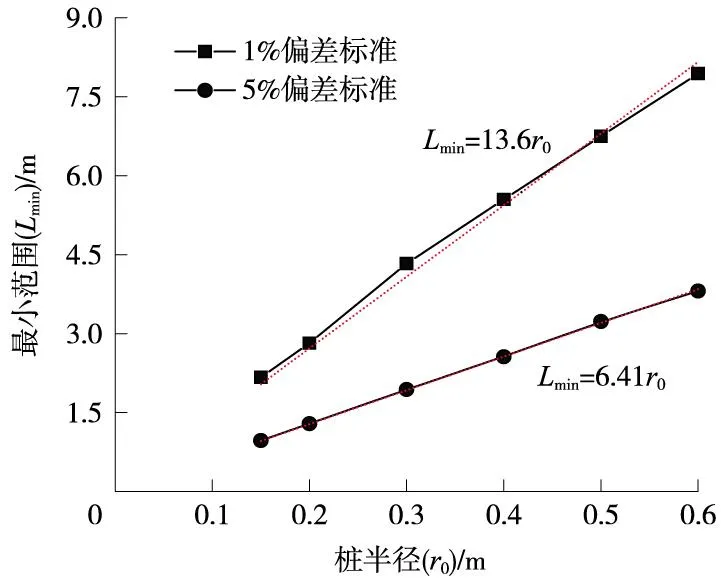
图6　最小范围关于桩半径拟合曲线

4结论

通过集中荷载作用解析解和考虑桩径影响的均布荷载数值积分解答关于Mindlin附加应力系数计算结果的对比分析，得到桩径、桩长以及土体泊松比对Mindlin附加应力系数的影响规律，确定Lmin主要决定因素为桩径，并由数据拟合方法得到Lmin关于桩半径r0的拟合公式，主要得到以下几点结论。

(1)土体泊松比对Mindlin附加应力系数计算结果的影响很小，统一采用0.35泊松比引起的附加应力计算偏差一般不超过10%。

(2)桩径相对大小影响Mindlin附加应力系数计算结果，但存在影响范围；当附加应力计算点与荷载作用点距离超过某一特定限值时，桩径引起的Mindlin附加应力计算偏差将可忽略。

(3)Mindlin附加应力系数计算中，必须考虑桩径影响的最小范围Lmin，其主要决定于桩径，随桩径的增加而增大；分别采用1%和5%附加应力系数偏差控制标准时，当附加应力计算点与荷载作用点距离分别超过13.6r0和6.41r0，即可统一采用集中荷载附加应力解析表达式计算Mindlin附加应力。

参考文献：

[1]王士杰，张梅，张吉占.Mindlin应力解的应用理论研究[J].工程力学，2001，18(6):141-148.

[2]GEDDES J D. Stress in foundation soils due to vertical subsurface loading[J]. Geotechnique， 1966，16(3):231-255.

[3]杨敏，王树娟，王伯钧，等.使用Geddes应力系数公式求解单桩沉降[J].同济大学学报：自然科学版，1997，25(4):379-385.

[4]金永涛，杨桦，李峰利.桩筏共同作用的改进Geddes计算模型与变刚度调平设计[J].岩土力学，2010，31(12):3875-3878.

[5]杨明，张可能，刘杰.柔性基础下复合地基有效桩长计算方法研究[J].郑州大学学报：工学版，2008，29(2):23-26.

[6]徐志英.以明特林(Mindlin)公式为根据的地基中垂直应力的计算公式[J].土木工程学报，1957，4(4):485-496.

[7]艾志勇，杨敏.广义Mindlin解在多层地基单桩分析中的应用[J].土木工程学报，2001，34(2):89-95.

[8]周罡，林荫.用Mindlin应力解求单桩沉降的方法[J].地下空间，2001，21(3):173-177.

[9]MINDLIN R D. Force at a point in the interior of a semi-infinite solid[J]. Physics， 1936，7(5):195-202.

Research on Pile Radius Influence on the Coefficient of Mindlin Additive Stress

GUO Shuai-jie1，2，3， SONG Xu-guo1，2， XU Zai-liang1， SUI Xiao-min1， REN Qing-chang1

(1.The Third Railway Survey and Design Institute Group Corporation， Tianjin 300251， China;

2.Laboratory of Rail Transportation Survey and Design， Tianjin 300251， China;

3.Southwest Jiaotong University， Chengdu 610031， China)

Abstract：Based on the analytical solution of Mindlin theory for the additive stress calculation induced by point loading， relationship between pile radius and Mindlin additive stress coefficient is discussed in detail with different poisson ratio and pile length. Subsequently， the minimum influence range of pile radius under different error standard is determined， and the fitting equation of influence range is obtained accordingly. Research results indicate that the influence of the soil poisson ratio on the additive stress is at a very low level， and the greatest error is normally less then 5% if the poisson ratio value of 0.35 is applied. During the calculation of Mindlin additive stress coefficient， the minimum influence range of pile radius is mainly determined by pile radius， and would keep increasing with the increasing of the pile length. Moreover， if error standards of 1% and 5% are accepted respectively， the minimum influence range of pile radius should be 13.6 and 6.41 times of the pile radius respectively.

Key words：Mindlin method; Additive stress; Pile radius; Pile length; Influence range

作者简介：郭帅杰(1987—)，男，工程师，在站博士后，2014年毕业于河

基金项目：中国铁路总公司科技研究开发计划项目(2014G003-B)

收稿日期：2015-06-08

中图分类号：TU473.12

文献标识码：ADOI:10.13238/j.issn.1004-2954.2016.01.002

文章编号：1004-2954(2016)01-0008-06