基于ISM的作战仿真模型体系结构建模*
郑世明,王洪军,孙 涛
(南京陆军指挥学院,江苏南京 210045)
基于ISM的作战仿真模型体系结构建模*
郑世明,王洪军,孙涛
(南京陆军指挥学院,江苏南京210045)
摘要:作战仿真模型体系结构的描述是一个复杂的问题,传统的方法难以清晰描述各要素之间的内在关系。采用解释结构模型的方法对模型体系中的继承、组合关系进行形式化建模,在对体系要素进行简化抽象的基础上,通过矩阵运算和逻辑推理完成对体系内所有要素的关系描述,能够实现对复杂模型体系的结构化描述和简洁化表达。
关键词:模型体系;解析结构模型;形式化分析;作战仿真
修回日期: 2015-11-04
王洪军(1975-),男,博士,副教授,硕士生导师。
孙涛(1976-),男,博士,副教授。
模型体系设计的基础是结构建模,模型体系中除了包含大量的模型之外,还存在多种复杂的关系,因此,模型体系的设计首先要对其结构进行建模和分析,需要关注到模型在体系中是按照怎样的方式分类的,模型之间的关系是怎样构建的,采用形式化方法对模型体系进行建模,可使模型在体系中具有统一性和规范性。解析结构模型(Interpretive Structural Model),是在图论的基础上,按照重构的思想对系统结构进行建模的一种方法,主要是用来分析组成复杂系统的要素以及要素之间的关系,通过建立各要素之间的内在逻辑关系,形成具有良好表达结构的描述形式,对于复杂的作战仿真模型体系而言,在对各模型进行关系建模的基础上,只要通过矩阵的逻辑演算,定性和定量相结合的方法,就能很好地处理复杂模型体系描述问题。
1基本概念[1]
假设某复杂系统X的要素集为(s1, s2,…, sn),描述系统的可达矩阵为M=(mij)n×m,n为要素个数,m为描述要素的维度。
定义1没有回路的上位集 要素si没有回路的上位集记作A(si),其中A(si)中的要素与si无关,而si与A(si)中的要素有关,即有向图上从si到A(si)存在有向边,而从A(si)到si不存在有向边。
定义2有回路的上位集 要素si有回路的上位集记作B(si),其中B(si)中的要素与si有关,而si与B(si)中的要素也有关,即有向图上从si到B(si)存在有向边,而从B(si)到si也存在有向边。
定义3无关集 要素si的无关集记作C(si),其中C(si)中的要素与si无关, si与C(si)中的要素也无关,即有向图上从si到C(si)不存在有向边,而从C(si)到si也不存在有向边。
定义4下位集 要素si的下位集记作D(si),其中D(si)中的要素与si有关,而si与D(si)中的要素无关,即有向图上从si到D(si)不存在有向边,而从D(si)到si存在有向边。

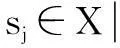

图1 要素si与其上位集、无关集和下位集之间的关系
2ISM方法步骤
解释结构模型ISM是美国华费尔教授于1973年作为分析复杂社会经济系统有关问题的一种方法而开发的,其目的是通过将复杂的系统分解为若干个子系统,分析各个子系统之间及其内部的关系,最终将复杂系统构造成一个多级递阶的结构模型[2]。
其基本步骤分为:
1)根据具体的问题,选择构成问题的要素,即系统包含的具体要素和对象有哪些;
2)基于某种关系构建可达矩阵。系统内的要素之间一定存在着某种关系,由于建模目的不一样,这种关系可以是继承关系、组合关系、关联关系、聚合关系等;
3)根据可达矩阵,按照区域分解、区域内分级的思路分析并建立结构解析模型[3-4]。
下面利用一个实例对仿真模型体系的结构进行分析,分别对模型的继承关系、组合关系进行建模分析。
3继承关系建模
继承关系是面向对象设计方法的重要手段,对继承关系建模的目的在于能够对模型进行合理分类,理顺体系中模型之间的继承关系,建立模型的层次结构,利用有向图描述模型之间的关系,并形成相应的结构矩阵,以矩阵的形式表达较为复杂的继承关系,并通过矩阵计算和变换使复杂的关系转换成简单、直观的结构模型,便于在程序设计阶段能够以一种最简化的方式实现模型间的灵活运用。
对图2中的模型分别进行编号,令a1为仿真实体,a2为机动模型,a3为传感器模型,一直到a21为分析评估模型,可以得到模型的集合M={a1,a2,…,a21}。由图可知,根据模型之间的继承关系构建的模型体系结构为


图2 仿真模型体系实例(继承关系)
其中1表示两个模型之间有直接继承关系,0表示模型之间没有直接继承关系。根据解析结构模型方法的步骤对HS进行区域分解,得到可达性集合、先行集合和共同集合,如表1所示。

表1 模型体系的可达集、先行集和共同集(继承关系)
其他模型的L(ai)=∅,因此有共同集G=∅,所以经区域分解π(HS)={p1}=M,由此可知,模型体系只能分为一个区,也就是说所有的模型通过继承根类a1构成一个体系,从实际情况看,符合模型体系的划分规则,基本体现了模型的应用实际。
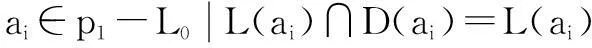
p1-L0-L1-L2={a1,a3,a13}≠∅,所以还需要继续分解
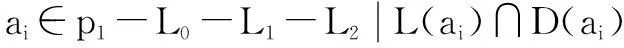
=L(ai)}={a13}
p1-L0-L1-L2-L3={a1,a5}≠∅

=L(ai)}={a5}
p1-L0-L1-L2-L3-L4={a1}≠∅

=L(ai)}={a1}
p1-L0-L1-L2-L3-L4-L5=∅
因此,模型可以分为五级L1,L2,L3,L4,L5,与图2中的层次结构是一致的,其中L1中的模型没有子模型,L2,L3,L4中的模型既有父模型也有子模型,L5中的模型没有父模型,只有子模型。采用级间分解的方式,可以了解各模型在体系中的层次以及相互间的继承关系。采用ISM形式化方式对模型的继承关系进行描述,可以很方便地实现对具有复杂继承关系的模型体系进行描述,并能迅速得出各模型之间存在的继承关系,实现对复杂模型体系的结构化描述与分析。
4组合关系建模

图3 仿真模型体系示例(组合关系)
本文以一个简单的仿真实体模型体系为例,假设该体系中有机动组件、传感器组件、电子对抗组件、平台组件、通信组件、行动组件、认知组件和武器组件等构成,然而要形成具有一定仿真能力的模型实体,必然需要对这些组件进行组合使用才能具备完成作战任务的能力,假设某系统内模型具有组合关系的可达矩阵为

为了进一步分析模型的组合关系需要对M进行区域分解,首先需要找出各要素的可达性集合、先行集合以及共同集合,如表2所示。

表2 模型体系的可达集、先行集和共同集(组合关系)
由表2知G={a4,a8},由于L(a4)∩F(a8)=∅,所以a4,a8分别属于两个区域中。另外,由于a5,a6和a7的可达集合交集非空,所以a5,a6,a7和a4在同一区域,故系统可划分为两个区域π(X)=P1,P2,其中P1={a4,a5,a6,a7},P2={a2,a3,a8},依据区域划分的结构,可将可达矩阵中的要素进行重新排列,得到矩阵MH:
从以上可以看出,MH与矩阵M不同,在结构上更为清晰。根据表2,按照区域内级间分解的方法对其进行区域间层级分析。


表3 a4,a5,a7的可达集、先行集和共同集

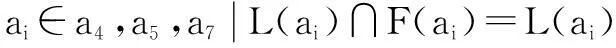
={a4,a7}
即第二级要素为a5和a7,剩余要素为{a4},如表4所示。

表4 a4的可达集、先行集和共同集


即第三级要素为a4,剩余要素为∅,至此,所有要素均被分级,故区域P1共分为三级。



在区域划分和级间分解的基础上,分析并建立组合结构模型,求解组合结构模型实际上就是要建立结构矩阵,这个结构矩阵主要用来反映系统多级递阶结构的问题。下面以一种简化方法分析并找出结构矩阵,即通过将矩阵M′减去单位矩阵I,得到新的矩阵M″,实际上是一个对系统整理而求得的可达性矩阵再还原回去的过程,这种抽象和转换使得对体系的认识更加具体、直观,并能从结构中直接抽取本质属性和关系。
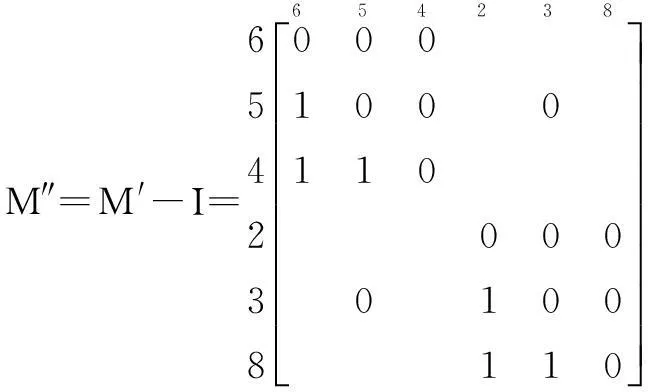
在矩阵M″中,先找一级与二级之间的关系,再找二级与三级之间的关系,直到将每一个分区的各级找完为止,则可得到结构矩阵A′。从M″中知m″56=1,说明节点a5与处于第一级的节点a6有组合关系,即a5→a6,然后抽去a6的行和列再找第二级与第三级之间的关系,又知m″45=1,说明节点间a4与a5有组合关系,以此类推,可以将P2区域中的节点间关系也找出来,m″32=1,m″83=1,最后将m″56=1,m″45=1,m″32=1,m″83=1作为结构矩阵的元素,画出结构矩阵A′如下:

有了结构矩阵A′,就可以绘制出体系的多级递阶有向结构图,如图4所示。
从图4可以看出:机动模型、传感器模型和认知模型可以按照一定方式建立组合关系,并形成一个更加复杂的组合模型。因此,在仿真过程中如此复杂的过程可以通过这样一个组合的复杂模型直接完成。采用ISM形式化方式对模型的组合关系进行描述,可以很方便地实现对具有复杂组合关系的模型体系进行描述,并能够清晰、直观地构建出更加复杂的组合模型。
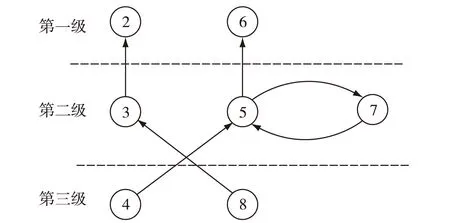
图4 多级递阶有向结构图
5结束语
本文采用ISM体系结构建模方法,对作战仿真模型体系的构成要素以及要素之间的关系进行分析,构建邻接矩阵和可达矩阵,在分析可达矩阵的基础上,建立作战仿真模型体系解析结构模型。通过对各要素之间的层次结构关系描述,采用体系结构建模方法对模型体系中的继承关系、组合关系进行了形式化建模,并通过具体实例分析了内在关系。
参考文献:
[1]陈欣.美军建模仿真对象模型体系框架研究[M].北京:军事科学出版社,2008:12-16.
[2]张琦.使命空间功能描述理论和方法研究[D].长沙:国防科技大学,2005:32-37.
[3]李宏权,邓桂龙.战役训练模型服务体系与技术方法[M]. 北京:国防工业出版社,2012:7-8.
[4]周东详.多层次仿真模型组合理论与集成方法研究[D]. 长沙:国防科学技术大学,2007:85-95.
[5]汪应洛.系统工程[M]. 北京:机械工业出版社, 2003:45-48.
[6]陈悦棠,王佳丽. 基于解析结构模型的团队合作质量影响因素研究[J]. 广西大学学报(哲学社会科学版),2010,32(1):243-245.
[7]丁容,陆伟刚.基于ISM模型的企业隐性知识转移影响因素分析[J].当代财经, 2010,2(2):74-77.
[8]汪滢,张清风,戴锋.解析结构模型在军队信息化建设中的应用[J]. 军事经济研究,2008,29(4):14-16.
Modeling of Architecture of Combat Simulation Models Based on Interpretive Structural Model
ZHENG Shi-ming, WANG Hong-jun, SUN Tao
(Nanjing Army Command College, Nanjing 210045, China)
Abstract:The description of the architecture of the combat simulation model is a complex problem, the traditional method is difficult to describe the relationship between the elements. In this paper, we mainly use the method to explain the interpretive structure model of the model system in the inheritance and combination, on the basis of simplifying the system elements, the relationship between all elements of the system is described by matrix operation and logical reasoning, which can implement a structured description of complex model system and concise expression.
Key words:architecture of models; interpretive structural model; analysis for formalization; combat simulation
作者简介:郑世明(1981-),男,江苏扬州人,博士,讲师,研究方向为作战仿真与军事运筹。
*基金项目:中国博士后科学基金资助项目(2013M532132);总部项目(14KJ39)
收稿日期:2015-09-27
中图分类号:TP391.9;E917
文献标志码:A
DOI:10.3969/j.issn.1673-3819.2016.01.006
文章编号:1673-3819(2016)01-0023-05

