旅游路线个性化推荐算法比较分析

李 霞，尹川东，袁 云

(1.广东外语外贸大学语言工程与计算实验室，广东广州 510006; 2.广东外语外贸大学信息学院，广东广州 510006)

旅游路线个性化推荐算法比较分析

李 霞1，尹川东2，袁 云2

(1.广东外语外贸大学语言工程与计算实验室，广东广州 510006; 2.广东外语外贸大学信息学院，广东广州 510006)

随着自助游群体的增加，越来越多的人希望能够在满足用户特定需求(如限定旅游天数、旅游费用、住宿标准等)的前提下，获取自动生成的可供参考的包括旅游景点、价格和住宿一体化的旅游推荐路线，并能够可视化呈现给用户。蚁群算法和遗传算法是0-1背包问题中的两种经典算法，通过建立应用于个性化旅游路线推荐问题中的数学模型，将蚁群算法和遗传算法应用于旅游路线个性化推荐中。依据文中所提出的最优路线推荐分值评价方法，对所选取的推荐算法进行了分析和测试。实验结果表明，优化后的蚁群算法和遗传算法均优于传统蚁群算法和遗传算法，并且从综合性能看，基于贪心解的混合遗传算法可有效应用于旅游路线个性化推荐中。

旅游路线自动规划;旅游挖掘;遗传算法;贪心算法;最大最小蚁群算法

0 引言

个性化旅游路线推荐是指依据用户喜好、设定相对应的参数，如旅游总价格、旅游时间、入住酒店等条件因素所获取的最佳旅游个性化路线推荐。现有算法中，遗传算法和蚁群算法被广泛应用于地图搜索、路线规划和0-1背包问题中［1-4］。现有研究中，有针对群体的旅游路线推荐算法，如宋晓宇等［5］针对旅游中常见的现象—结伴出行，研究并提出了群体旅游路线推荐问题，目标是为群体推荐一条能够使群体整体满意度大，个体满意度差异小，对群体内所有成员较公平的最优群体旅游路线。通过分析聚合用户偏好时通常采用的平均数策略与无痛苦策略在推荐结果方面存在的不足，针对搜索路线所具有的动态性特点，提出了一种动态聚合用户偏好的策略，基于该策略建立路线评价模型，对路线进行满意度评分，返回分值最高的路线，并验证了算法在不同参数设置下的有效性。Wang Qingfeng等［6］提出将人工免疫算法和蚁群算法结合的混合算法用于旅游路线的规划中。Shi Linan等［7］提出了针对改进蚁群算法的旅游路线规划算法。任竞斐等［8］建立了Logit模型，将游客在不同路线上进行分配，建立了综合游客偏好、拥挤度、等待时间和行走时间等指标的旅游效用函数，减少了旅游高峰期游客拥挤和等待的情况。模拟仿真表明，提出的方案要明显优于基于最短路径的路线选择方案。夏亚梅等［9］对基本蚁群算法进行研究和改进，建立了一个服务组合模型，可以适应服务组合优化过程。黄翰等［10］通过给出估算蚁群算法期望收敛时间的理论方法，研究和分析了蚁群算法的收敛速度。郑立平等［11］通过混合使用多种杂交算子，获得求解旅行商问题的更优解。宋海生等［12］提出了基于贪心解的混合遗传算法，并应用于背包和多维0-1背包问题中。

已有研究中，并没有针对蚁群算法、遗传算法及其优化算法在旅游路线推荐中的性能比较分析，文中在爬取互联网中的旅游数据基础上，将蚁群算法、遗传算法、最大最小优化蚁群算法和基于贪心解的混合蚁群算法应用于旅游路线推荐中，并分别从所选出路线的平均评价分值、最优评价分值、算法所耗费时间三个方面对算法进行评价比较。实验结果表明，最大最小优化蚁群算法和基于贪心解的混合蚁群算法可有效应用于旅游路线自动化推荐中。

1 遗传算法

1.1 解决旅游路线规划上的数学模型

为了和基本遗传算法进行比较，文中参考了文献［7］中所提出的混合遗传算法的思想，并将所提出的混合遗传算法应用于旅游路线推荐问题中，所涉及到的数学模型主要包括染色体编码、适应度函数以及选择算子，详细模型描述如下:

(1)染色体编码。

将用户的游览路线用二进制编码表示，例如10维度下的染色体(0，1，0，1，0，0，0，0，0，1)表示景点2，4，10被选入当前路线中。

(2)适应度函数。

遗传算法中较为关键的是适应度函数，它被用于评价和选择染色体，并将影响到该个体在选择算子中的遗传概率，是遗传算法是否能够达到最优代的关键因素。适应度函数的选取直接影响到遗传算法的收敛速度以及能否找到最优热度，文中选择的适度函数如下:

其中，fit(f(x)，g(x))为旅游景点 x的适应度; f(x)为该景点费用的目标优化函数，由景点门票价格等信息组合而成;g(x)为该景点热度的目标优化函数，表示景点游玩人数总和;Amin为花费的最小值，Amax为花费的最大值;γ为花费的缩放系数，μ为热度的缩放系数，γ，μ的作用是防止花费或者热度数值波动过大;ρ为惩罚系数，为了平衡花费和热度对适度的影响。

(3)选择算子。

1.2 基于贪心策略的混合遗传算法

在解决旅游路线规划问题上，传统遗传算法的编码不能全面将优化问题的约束表示出来。同时，遗传算法容易过早收敛，可能无法搜索到全局最优路径。遗传算法的过早收敛、效率低等问题主要是因为初始种群采取了随机方式，这导致遗传算法需要大数量的进化代数，且进化代数跟种群的大小呈正比。当种群达到一定规模时，遗传算法的效率会降低，并且可能收敛于局部最优，无法达到最优热度。同时应用于旅游大数据时，进化代数的增加将极大增加算法的时间效率。

为了能够和传统遗传算法在旅游路线推荐效率上进行比较分析，文中选取了文献［4］所提出的基于贪心解的混合遗传算法(MGGA)，并将其应用于旅游路线推荐中。算法的第一阶段，先对旅游景点进行评分，根据分值将旅游景点按降序排列，依次将景点放入路线内，直至超出最大游玩时间为止。算法的第二阶段，先用贪心算法生成问题的贪心解，然后在遗传算法的进化过程中，让每一代最差适应度的个体无条件地变为此贪心解。算法详细描述如下:

(1)算法第一阶段。

Input:原始个体染色体编码chromosome，景点热度数组hotness，景点游玩时间数组visitDays;

Output:经过优化的染色体编码chromosome。

Step1:根据个体染色体编码，找出未加入路线的景点;

Step2:将这些景点按照热度(即景点旅游人数的总和)，从大到小依次放入时间小于当前路线游玩天数景点至不能再放入任何景点。

(2)算法第二阶段。

Input:景点热度数组hotness，游玩时间数组visit-Days，路线游玩时间upDays，交叉率Pc，变异率Pm，种群规模scale，遗传代数maxGen;

Output:最优热度的染色体chromosome。

Step1:使用贪心算法随机求得scale个贪心解作为初始种群，其中scale为种群规模。

Step2:将Step1中的初始种群进行二进制编码(其中第i位为1表示第i个景点被选择，若为0，则表示第i个景点未被选择)。

Step3:按照1.1节所定义的适应度函数计算群体中每个个体的适应度。

Step4:将以上个体作为第0代，记录此代最高适应度的个体。

Step5:当此代的适应值不满足最高要求并且当前代数小于初始化设定的最大代数时，执行Step5.1-5.6并循环，否则，执行Step6。

Step5.1:执行选择算子;

Step5.2:以Pc执行交叉算子;

Step5.3:以Pm执行变异算子;

Step5.4:计算此代的适应值，方法同Step3;

Step5.5:找出适应度最差的个体，将其通过贪心算法优化;

Step5.6:用此代最高适应度的个体适应值与上次所记录的最高适应度的适应值进行比较，若比上一次好，则将此个体记录为当前最高适应度个体。

Step6:打印最佳解的选择个数、所选景点的总分值数和总花费。

2 蚁群算法

2.1 蚁群算法解决旅游路线规划的数学模型

旅游路线规划并不是TSP问题，而是类似于0-1背包问题。旅游的天数类似于0-1背包问题中背包的容量，景点的热度则类似于0-1背包问题中每个物品的价值，所不同的是，在旅游路线规划中景点的热度由游玩人数、门票价格、评论数等得分共同构成。景点被选择的概率Pki(t)为:

信息素的更新为:

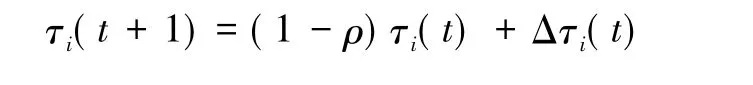
其中，ρ为信息素挥发因子，1-ρ表示信息的残留系数，ρ的取值范围一般为［0，1］;Δτi(t)为所有蚂蚁在景点i上的信息素总和，即Δτi(t)=τki(t)，(t)为第k只蚂蚁在第t代循环中留在景点i的信息量，采用Ant-Cycle模型进行更新，其公式如下:

其中，Q为一个常量，表示蚂蚁完成一次完整的路径搜索后所释放的信息素总量，它在一定程度上影响算法的收敛速度;Lk表示第k个蚂蚁在t代循环中所走路径的总长度，即热度的总和。

2.2 最大最小优化蚁群算法

蚁群算法在旅游路线推荐中，由于缺乏参考选择路径使得景点搜索时间长，同时算法容易出现某景点因为一直不被采纳而变的权重极低，使得后续路线无法选择该景点，从而停滞的现象。最大最小优化蚁群算法［13-14］对原始蚁群算法做了以下改进:

(1)每次循环完之后，选出最佳蚂蚁，最佳蚂蚁可以留信息素，其他蚂蚁都不留。

(2)为了防止所有信息素都被蒸发掉，最后只剩下最佳蚂蚁的路径，MMAS采用很小的蒸发率，从而保证所有路径不会迅速变为0。

(3)强制所有路径的信息素有最大值和最小值限制，高于低于这个范围都会被自动设置为最大值或者最小值，因此信息素的范围在［τmin，τmax］之间，从而保证最少信息素的路径也有机会被选择。

(4)为了使蚂蚁在算法的初始阶段能够更多地搜索新的解空间，最大-最小蚁群系统将τmax设置为每条边上的信息素初始值s。

(5)使用轮盘赌注方法计算景点被选择的概率，使得更多的路线可以被挖掘。

3 实验

3.1 实验数据

实验中涉及到景点数据和酒店数据。其中，景点数据包括景点拼音、景点名、游玩人数、门票价格、推荐游玩时间和大地坐标;酒店数据包括酒店名称、酒店地址、酒店电话、酒店评论得分和酒店价格。图1分别展示了文中的景点数据和酒店数据的jason格式。

3.2 实验评估模型

实验选取广州市的451个景点和该景点周围的酒店数据，其中景点数据从百度旅游网站中爬取，酒店数据则从马蜂窝网站上爬取，所爬取的数据库截图如图2所示。

3.3 评价模型

为了选取最优路线，文中建立了一个应用于评价是否为最优旅游路线的评估模型。建模思想是:所选出的旅游路线优先考虑热门景点且景点门票价格和酒店费用总和较低，为此定义了一个旅游路线的最优分值函数，该函数被用于评价不同算法在挖掘得到的旅游路线的评分值，分值高表示该路线优。

其中，Score(x)为算法计算所得到旅游路线的最优分值;f(x)为该路线门票费用和酒店费用之和; g(x)为该路线游玩人数之和;Amin为花费总和的最小值;Amax为花费总和的最大值;γ为花费的缩放系数;μ为热度的缩放系数;ρ为花费的惩罚系数。

γ，μ的作用是将Score限制在一个范围中，防止过大的波动;ρ的作用是为了平衡花费和热度对适度的影响。在该模型中，游玩人数占主导优势，当两条路线游玩人数相当时，价格便成为了决定因素，价格较低的路线热度更大。

3.4 实验结果

所有实验均在系统为MacOSX 10.10 Yosemite、处理器为2.2 GHz Intel Core i7、内存为16 GB 1 600 MHz DDR3、硬盘为256 GB SSD的平台上进行。文中分别对蚁群算法(AS)和最大最小蚁群算法(MMAS)、遗传算法(GA)和提出的混合遗传算法(MGGA)在推荐路线的平均分值、最优分值、平均耗时三个参数上进行了对比，其中平均分值代表了算法的局部搜索能力和稳定性，最优分值代表了算法的全局搜索能力和准确性。

在AS和MMAS评测中，信息素更新公式中令α= 1，β=2，实验通过改变迭代次数和蚂蚁数量来测试算法的性能。每改变一次迭代次数或蚂蚁数量都将AS 和MMAS运行10次，去除重复路径之后，记录分值排名前20条路线的平均分值、最优分值和平均耗时，实验结果如表1所示。

实验结果表明，MMAS算法耗时明显小于传统蚁群算法，并且随着迭代次数和蚂蚁数量的增加，MMAS发现的解逐渐优于AS。

在GA和MGGA评测中，设置Pc=Pm=0.9，通过改变进化代数和种群规模来测试算法的性能。每改变一次进化代数或种群规模都将GA和MGGA运行10次，去除重复路径之后，记录分值排名前20条路线的平均分值、最优分值和平均耗时，实验结果如表2所示。

从表2可知，GA和MGGA的平均分值都与种群规模大小呈正比，总体上来看，随着进化代数的增加，GA和MGGA的平均分值逐渐增加，最终趋于稳定。在该实验中，对于MGGA，当进化代数达到100且种群规模达到500时，平均分值和最优分值达到最高，分别为104.77和114.62。

同时实验结果还表明，文中所提出的MGGA与GA相比，在耗时差别不大的前提下，所推荐出的旅游路线的平均分值和最优分值明显优于GA。另外，还分别计算了AS、MMAS、GA、文中算法在不同情况下所得到的推荐路线的平均分值、最优分值和消耗时间的平均值，实验结果表明在推荐路线的最优分值差异不大的情况下，MGGA所花时间小于MMAS，同时文中算法在时间与GA差异不大的前提下，所得到的旅游路线的最优分值大于GA。

4 结束语

文中选取经典旅游规划算法，在所爬取的旅游数据上，分别从所选取的旅游路线的平均分值、最优分值和耗费时间进行分析对比。实验结果表明，优化后的最大最小蚁群算法和基于贪心解的混合遗传算法的综合效率优于传统蚁群算法和遗传算法，可应用于系统实践中。

［1］ Cormen T H，Leiserson C E，Rivest R L，et al.Introduction to algorithms［M］.2nd ed.［s.l.］:MIT Press and McGraw-Hill，2001.

［2］ Dréo J，Siarry P P，Pétrowski A，et al.Metaheuristics for hard optimization［M］.［s.l.］:［s.n.］，2006:123-150.

［3］ Dubitzky W，Wolkenhauer O，Cho Kwang-Hyun，et al.Encyclopedia of systems biology［M］.［s.l.］:［s.n.］，2013.

［4］ 张文修，梁 怡.遗传算法的数学基础［M］.西安:西安交通大学出版社，2001.

［5］ 宋晓宇，闫玉奇，孙焕良，等.基于签到数据的群体旅游路线推荐［J］.计算机科学与探索，2015，9(1):51-62.

［6］ Wang Qingfeng，Wang Yuhui.Route planning based on combination of artificial immune algorithm and ant colony algorithm ［M］//Foundations of intelligent systems.Berlin:Springer-Verlag，2011:121-130.

［7］ Shi Linan，Li Li，Zhao Wenjing，et al.A delay-constrained multicast routing algorithm based on the ant colony algorithm ［C］//Proceedings of the international conference on information engineering and applications.［s.l.］:［s.n.］，2012:875-882.

［8］ 任竞斐，郑伟民.景区旅游高峰期游客旅游路线动态实时调度仿真研究［J］.统计与决策，2013(8):42-45.

［9］ 夏亚梅，程 渤，陈俊亮，等.基于改进蚁群算法的服务组合优化［J］.计算机学报，2012，35(2):270-281.

［10］黄 翰，郝志峰，吴春国，等.蚁群算法的收敛速度分析［J］.计算机学报，2007，30(8):1344-1353.

［11］郑立平，郝忠孝.基于混合杂交的遗传算法求解旅行商问题［J］.计算机工程，2005，31(20):168-169.

［12］宋海生，宋海洲，傅仁毅，等.求解多限制0-1背包问题的混合遗传算法［J］.计算机工程，2009，35(13):4-7.

［13］Dorigo M，Gambardella L M.Guest editorial special section on ant colony optimization［J］.IEEE Transactions on Evolutionary Computation，2002，6(4):317-319.

［14］ Dorigo M，Gambardella L M.Ant colonies for the traveling salesman problem［J］.Bio-Systems，1997，43(2):73-81.

Comparison and Analysis of Personalized Recommending Algorithm of Travelling Route

LI Xia1，YIN Chuan-dong2，YUAN Yun2
(1.Laboratory of Language Engineering and Computing，Guangdong University of Foreign Studies，Guangzhou 510006，China; 2.Informatics School，Guangdong University of Foreign Studies，Guangzhou 510006，China)

With the increasing of self-driving tours population，more and more people want to get the automatically generated route based on their specific needs，like special traveling days，traveling fees，special hotel expense quarterage.Ant colony algorithm and genetic algorithm are two classical algorithms used in 0-1 Knapsack Problem.It builds a mathematic model in this paper which can be applied to automatically generated route.An evaluation method for assessing the best compatible recommending traveling route is also given，which is used to analyze and test the selected algorithms.The results from the experiment show that optimized ant colony algorithm and the hybrid genetic algorithm outperform the basic ant colony algorithm and genetic algorithm.And also found that the hybrid genetic algorithm can be used in the traveling route recommending system from synthetic property.

traveling route planning;traveling mining;genetic algorithm;greedy algorithm;maximum and minimum ant colony algorithm

TP301.6

A< class="emphasis_bold">文章编号:1

1673-629X(2016)09-0073-05

10.3969/j.issn.1673-629X.2016.09.017

2015-08-11

2015-12-16< class="emphasis_bold">网络出版时间:

时间:2016-08-23

广东省普通高校科技创新项目(2013KJCX0071)

李 霞(1976-)，女，副教授，研究方向为文本挖掘。

http://www.cnki.net/kcms/detail/61.1450.TP.20160823.1343.024.html