杂交型椭球面网壳参数化设计及受力性能分析

鹿晓阳，付浩鑫，赵晓伟，陈世英，蒋雄，李涛

（1.山东建筑大学工程力学研究所，山东济南250101；2.山东建筑大学土木工程学院，山东济南250101）

杂交型椭球面网壳参数化设计及受力性能分析

鹿晓阳1，付浩鑫2，赵晓伟1，陈世英1，蒋雄2，李涛1

（1.山东建筑大学工程力学研究所，山东济南250101；2.山东建筑大学土木工程学院，山东济南250101）

杂交型椭球面网壳克服传统单一型椭球面和球面网壳随跨度S和环向区域份数Kn增加，结构顶点杆件数量增多而带来的杆件种类和尺度变化大等缺点，从而提高了结构的合理性，改善了结构的受力性能。文章根据杂交型椭球面网壳特点，采用APDL（Ansys Parametric Design Language）语言，研制了杂交型椭球面网壳参数化设计宏程序；以凯威特—肋环杂交椭球面网壳为例，应用ANSYS软件对其进行了受力性能分析。结果表明：同等工况下，凯威特—肋环杂交椭球面网壳顶点附近应力和位移均较小、且分布均匀，避免了单一网壳类型顶点附近应力集中现象，其受力性能优于单一类型凯威特、肋环型椭球面网壳；凯威特—肋环杂交椭球面网壳结构受力（2.35 N/m2）后的最大位移和最不利应力随跨度的增加而逐渐增大，当跨度S1≥110 m，Kn=6或Kn=8时最不利应力超过许用应力，工程中建议跨度上限为90～100 m。

杂交型椭球面网壳；参数化设计；受力性能分析

0 引言

随着我国城镇化速度的加快和建筑技术水平的提高，网壳结构优美的造型、合理的受力性能和多样的使用功能不断满足人们对大空间建筑的需要［1］。球面、柱面网壳及马鞍型网壳结构广泛应用于展览馆、体育馆和音乐厅等场所［2-5］，椭球面网壳不但给人带来舒适感且能更合理的利用自然采光和自然通风技术［6］。随着大跨空间建筑日益增多，人们已不满足传统单一网壳形式的直接运用。单一型椭球面和球面网壳随跨度和环向区域份数增加，结构顶点杆件数量增多，应力集中现象明显，施工困难。现在网壳结构更加倾向于不同结构形式的组合，更好地发挥各自特点，满足建筑美学且经济、合理。所以，新型结构形式杂交型网壳应运而生［7］。

新型杂交结构因几何构造简单、力流传递简明、室内建筑效果美观而受到建筑工程设计人员的青睐，杂交型椭球面网壳有效改善了肋环型、施威德勒型等单一椭球面网壳顶点附近应力集中及连接杆件较多的弊端，使网格分布均匀，结构受力性能得到明显改善。文章应用APDL参数化设计语言［8］，研制了杂交型椭球面网壳参数化设计宏程序，并以凯威特—肋环杂交型椭球面网壳为例，对其进行了12种工况受力性能分析和结构性能比对。

1 网壳结构杂交组合及几何描述

1．1 工程实例

椭球面网壳形式比较特殊，纵向较长、横向较短，近年来这种特殊的结构造型被广泛应用于实际工程当中，如广州亚运会自行车馆、温岭锦屏公园大门、上海科技馆、九寨沟甘海子国际会展中心、国家大剧院、北京奥体中心—鸟巢、北京奥运会羽毛球馆、中国石油大学校区体育馆等，如图1、2所示。其结构造型别致，且结构受力性能明显改善。

图1 网壳结构工程实例图

图2 杂交型网壳结构工程实例图

1．2 椭球面和球面网壳杂交组合

椭球面和球面网壳有六种网格形式：肋环型（Ribbed type）、施威德勒型（Schwedler type）、三向格子型（Three-way grid）、凯威特型（Kiewitt type）、联方型（Lamella type）和短程线型（Geodesic type）。网壳结构杂交组合需要满足两个条件［7］：

（1）在上、下两部分组合结构的过渡椭圆或圆上，两种结构形式的节点数必须相等；

（2）杂交组合应实现结构总体性能优化，即改善结构受力性能，也可降低结构总造价。

网壳结构杂交组合分为凯威特型为上部结构，有凯威特—肋环杂交型（Kie-Rib），凯威特—施威德勒杂交型（Kie-Sch），凯威特—联方杂交型（Kie-Lam）；三向格子型为上部结构，有三向格子—肋环杂交型（Thr-Rib），三向格子—施威德勒杂交型（Thr-Sch），三向格子—联方杂交型（Thr-Lam）。

1．3 椭球面结构几何描述

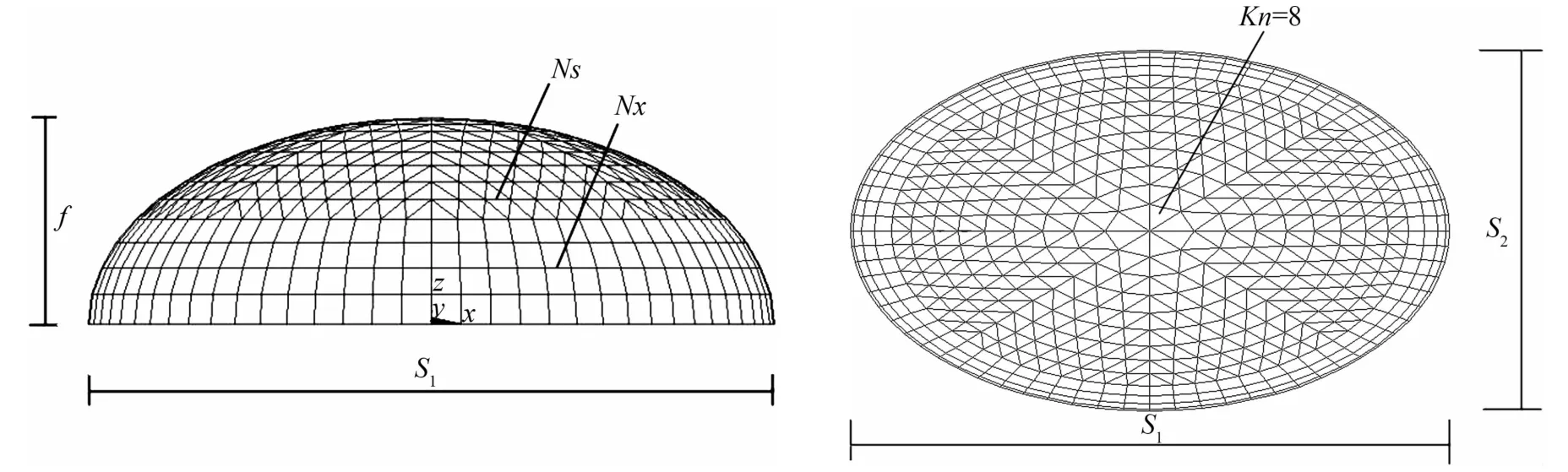
图3 凯威特肋环杂交型椭球面网壳宏观几何参数图（S1=60 m、S2=36 m、f=9 m、Kn=8、Ns=9、Nx=13）

杂交型椭球面网壳主要几何参数共有7个，长轴S1、短轴S2、矢高f、比例系数t、环向对称区域份数Kn、径向节点总圈数Nx和上部结构径向节点圈数Ns，如图3所示。其中比例系数t=1-i×（i+ 1）/［Nx×（Nx+1）］，（i=1，2，…，Nx），据比例系数t将矢高f进行统一划分，从而获得每一圈（或环）在矢高f上的投影坐标z。

2 杂交型椭球面网壳参数化设计

借鉴拓展型球面网壳、椭圆水平投影双曲抛物面网壳和折板网壳参数化设计思想［9-14］，研制了两类六种杂交型椭球面网壳参数化设计宏程序，现仅以凯威特—肋环杂交型椭球面网壳为例，进行参数化设计、受力性能分析和结构性能比对。

2．1 椭球面网壳参数化设计方法

给定椭球面网壳几何参数（S1、S2、f、t、Kn、Ns、Nx），在空间直角坐标系下，确定椭球面方程4x2/s12+4y2/s22+z2/f2=1，使用APDL循环语句由椭球面网壳顶点开始依次向外，据椭球面方程和比例系数t生成每一圈节点坐标并确定节点编号，再按不同网壳类型布杆规律连接相应节点生成杆件，从而形成各种椭球面网壳。具体步骤为

（1）输入模型形状参数 长轴S1、短轴S2、矢高f、比例系数t、环向对称区域份数Kn、径向节点总圈数Nx和上部结构径向节点圈数Ns；

（2）定义杆或梁单元类型、截面积（尺寸）及材料属性；

（3）生成节点 据所选网壳类型，应用APDL的循环语句，由几何关系和节点规律生成各节点；

（4）单元连接 据所选网壳类型和结构特点和网壳结构特定布杆规律，连接各节点，完成整个模型的建立。

2．2 凯威特—肋环杂交型椭球面网壳参数化设计

（1）计算各节点坐标并定义节点编号

令网壳顶点为1号节点，坐标为（0，0，f），按比例系数t划分矢高f、确定各环的z的坐标；据椭球面方程和Kn确定球半径R1、R2（R1=S1/2，R2= S2/2），求每一环节点的x、y坐标；然后再据确定的节点坐标（x，y，z），应用APDL循环语句，由顶点向外依次对第i圈、第j号节点进行节点编号，j+i×（i -1）×Kn/2+1（i=1，2，…Ns；j=1，2，…，Kn×i）。

建立下部结构肋环型节点，从第Ns+1圈开始由内向外依次进行，第j+Kn×（Ns×Ns+Ns）/2+1 +K0×（i-Ns-1）（Ns+1≤i≤Nx，1≤j≤K0，且K0=Ns×Kn）号节点坐标为x=R1×cos（360×（j-

（2）杆件连接

先进行上部结构凯威特型杆件连接。

环向杆件连接 在第i（i=1，2…Ns）圈、第j（j=1，2…，Kn×i-1）对称区内的节点循环，1+Kn×（i-1）×i/2+j与1+Kn×（i-1）×i/2+j+1（i =1，2…Ns；j=1，2…，Kn×i-1）连接生成一般对称区环向杆，1+Kn×（i-1）×i/2+1与1+Kn×（i-1）×i/2+Kn×i（i=1，2，…，Ns）连接生成最后一对称区环向杆。

径向杆件连接 先连接顶点1和第一圈各节点1+j（j=1，2，…，Kn），再从第2圈开始向外圈对各对称区循环，判断是否是当前对称区的最后一根杆并判断是否是最后一对称区，1+Kn×（j-1）×j/2+1与1+Kn×（j+1）×j/2+（k-1）×（j+1）+i（i =1，2…Ns；k=1，2，…，Kn；j=1，2…，i+1）连接，生成最后一对称区的杆件。1+Kn×（j-1）×j/2+（k -1）×j+i与1+Kn×（j+1）×j/2+（k-1）×（j+ 1）+i连接，生成非对称区内的杆件，由此形成凯威特型椭球面网壳上部结构。

从第Ns+1圈杆件的连接方式变为肋环型，即第i（Ns+1≤i≤Nx）圈、第j（1≤j≤K0-1）对称区域环向杆件是连接节点j+Kn×（Ns×Ns+Ns）/2+1 +K0×（i-Ns-1）和j+Kn×（Ns×Ns+Ns）/2+K0×（i-Ns-1）+2，第i圈最后一对称区域环向杆是由节点Kn×（Ns×Ns+Ns）/2+2+K0×（i-Ns-1）和节点Kn×（Ns×Ns+Ns）/2+1+K0×（i-Ns-1）+K0连接而成。径向杆件的连接是第Ns+1圈和第Nx圈之间的径向节点相连，由内向外循环第i圈、第j对称区域节点j+Kn×（Ns×Ns+Ns）/2+1+K0×（i-Ns-1）和节点j+Kn×（Ns×Ns+Ns）/2+1 +K0×（i-Ns）相连而成。

（3）过渡区（即第Ns圈和第Ns+1圈之间）杆件连接。因节点数相同，上下两环对应节点相连即可。形成的凯威特—肋环杂交型椭球面网壳结构模型如图4所示。

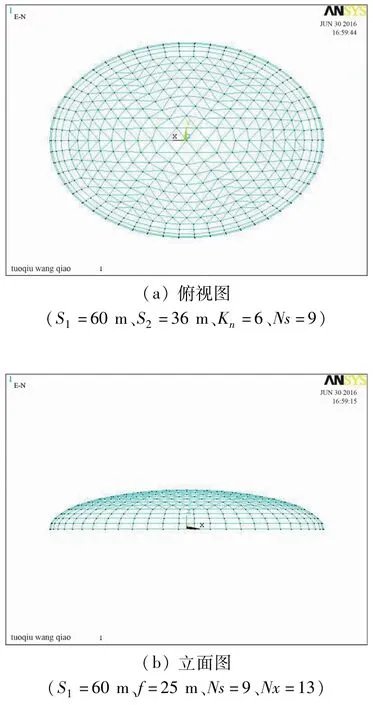
图4 凯威特—肋环杂交型椭球面网壳结构模型图

3 杂交型椭球面网壳受力性能分析

3．1 施加结构约束与载荷

网壳最外一圈节点采用可动铰支座约束（只限制x、y、z三个方向线位移，不限制转动），考虑结构自重（含杆件和节点）、屋面蒙皮等平均荷载，施加2．35 N/m2均布荷载［15］。

杆件采用Q235钢管，钢材密度为7850 kg/m3，弹性模量为2．06×1011N/m2，泊松比为0．3；杆件选用ANSYS中BEAM4梁单元，杆件截面为Φ219 mm ×16 mm；采用理想弹塑性材料模型，不考虑材料的强化、屈服阶段。

3．2 凯威特—肋环杂交型椭球面网壳宏观几何参数

当Kn=6、Kn=8、Nx=13、Ns=9时，分别选取不同跨度（S1、S2）与不同矢高（f）的凯威特—肋环杂交型椭球面网壳宏观几何参数见表1。

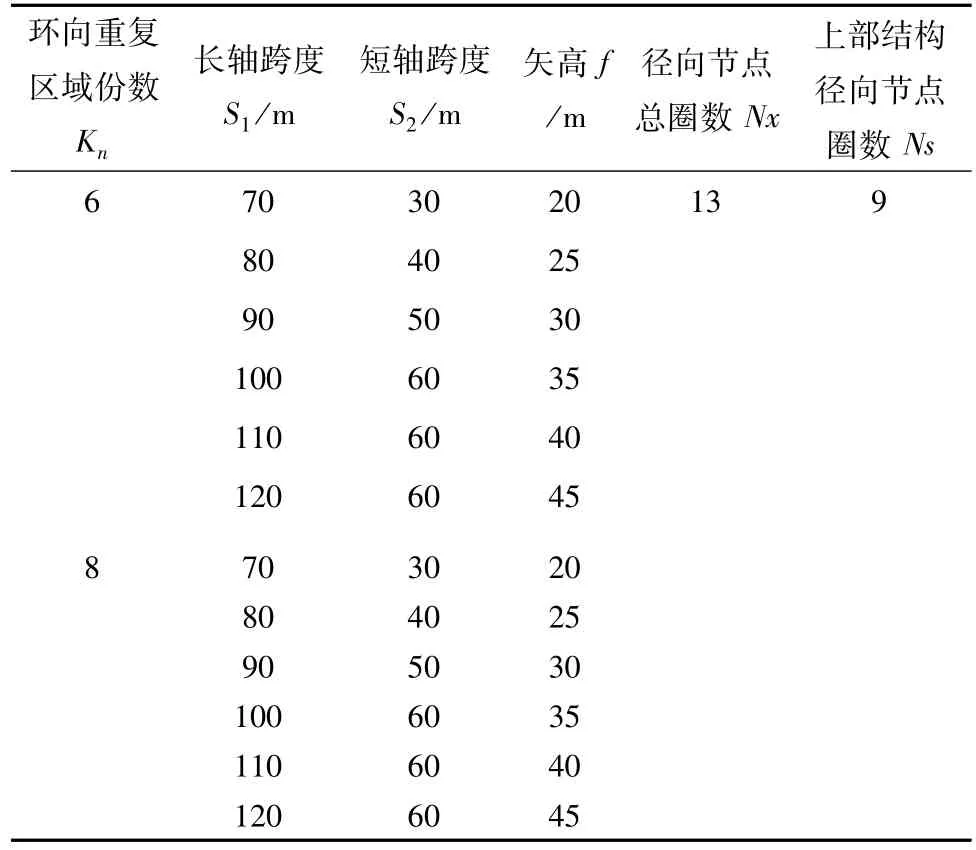
表1 凯威特—肋环杂交型椭球面网壳宏观几何参数

3．3 凯威特—肋环杂交型椭球面网壳受力性能分析

由JGJ 7—2010《空间网格结构技术规程》规定，单层网壳最大挠度不宜超过最短跨度的1/400，许用应力为钢材强度值215 MPa［16］。图5～8分别给出Kn=6时不同跨度和矢高下，杂交型椭球面网壳的位移云图和最不利应力云图。12种凯威特—肋环杂交型椭球面网壳结构受力性能分析结果见表2。表2中12种结构对应允许最大位移分别为0．075、0．1、0．125、0．15、0．15、0．15 m。

图5 Kn=6凯威特—肋环杂交型椭球面网壳位移云图

图6 Kn=6凯威特—肋环杂交型椭球面网壳最不利应力云图

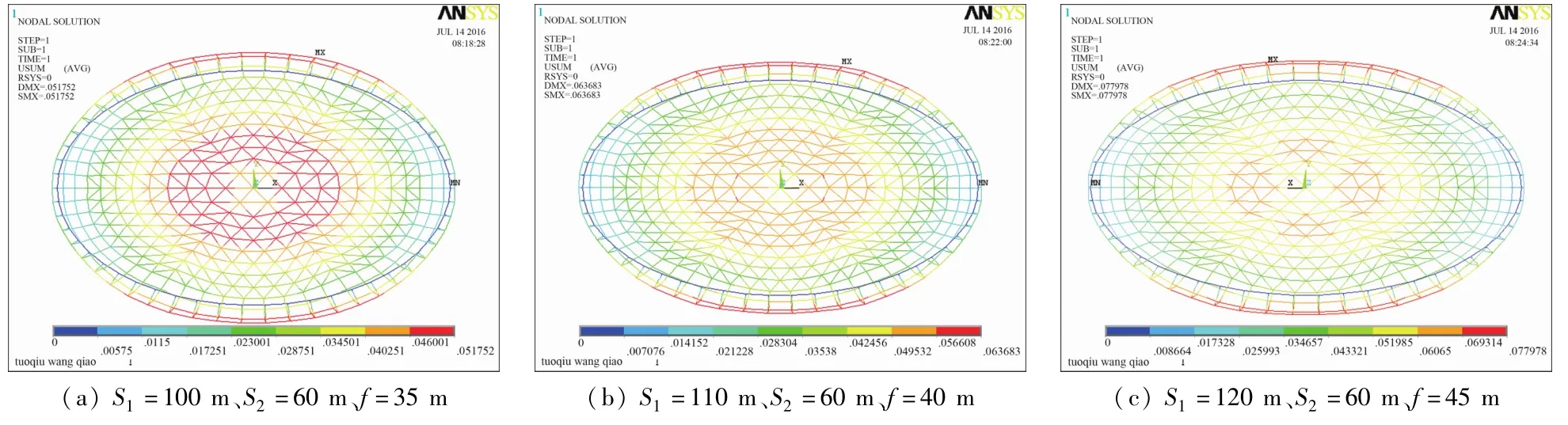
图7 Kn=6凯威特—肋环杂交型椭球面网壳位移云图

图8 Kn=6凯威特—肋环杂交型椭球面网壳最不利应力云图

图9～12分别给出Kn=8时不同跨度和矢高下，凯威特—肋环杂交型椭球面网壳的位移云图和最不利应力云图。

由图5～8和表2可知，Kn=6的六种不同结构尺寸的凯威特—肋环杂交型椭球面网壳，随着跨度（S1= 70～120 m，S2=30～60 m）和矢高（f=20～45 m）的增加，节点最大挠度（w=0．0189～0．0779）也在不断增加，但均满足结构刚度要求；当长轴跨度S1≥110 m时，最大应力为226 MPa，大于许用应力215 MPa。

由图9～12和表2可见，Kn=8的六种不同结构尺寸的凯威特—肋环杂交型椭球面网壳，随着跨度和矢高的增加（S1=70～120 m、S2=30～60 m、f=20～45 m），节点最大挠度（w=0．0195～0．0791）也在不断增加，但均满足结构刚度要求，当长轴跨度S1≥110m时，最大应力为222 MPa，大于许用应力215 MPa。

图9 Kn=8凯威特—肋环杂交型椭球面网壳位移云图

图10 Kn=8凯威特—肋环杂交型椭球面网壳最不利应力云图

图11 Kn=8凯威特—肋环杂交型椭球面网壳位移云图

图12 Kn=8凯威特—肋环杂交型椭球面网壳最不利应力云图

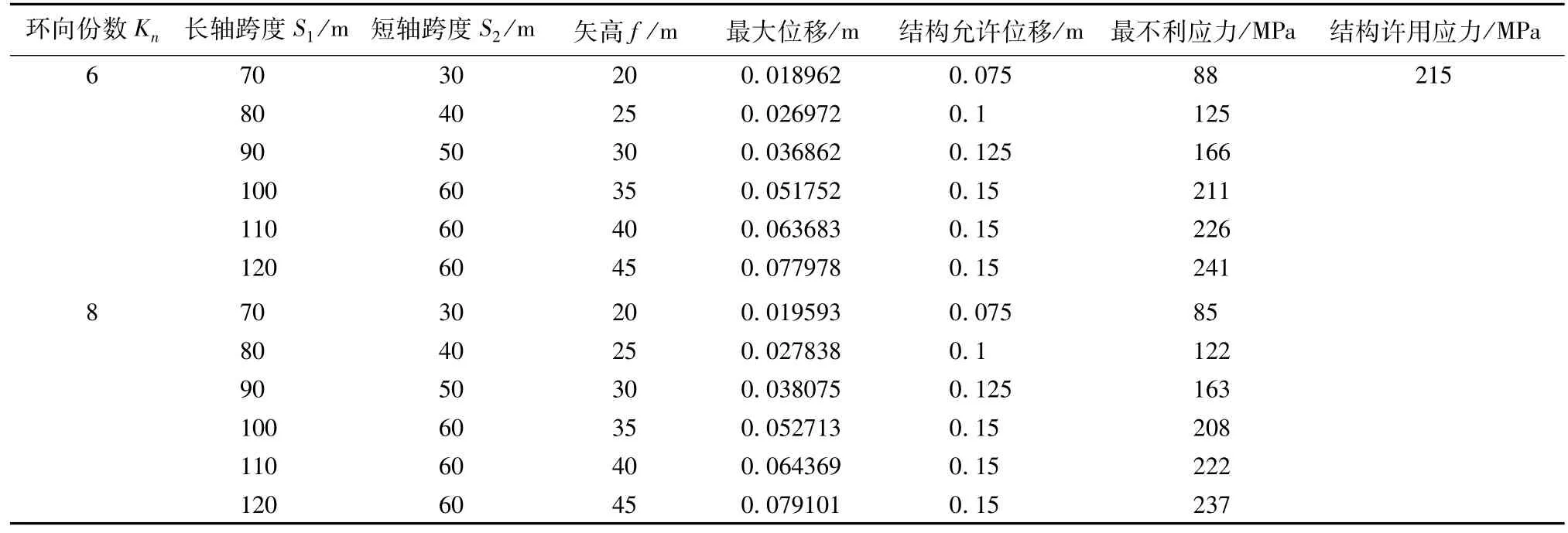
表2 凯威特—肋环杂交型椭球面网壳静力分析结果

3．4 杂交型与单一型椭球面网壳受力性能分析与结构性能比对

图13和14分别给出S1=100 m、S2=60 m、f= 15 m，凯威特—肋环杂交型椭球面网壳受力分析位移云图和最不利应力云图；图15和16分别给出S1=100 m、S2=40 m、f=20 m，凯威特—肋环杂交型椭球面网壳受力分析位移云图和最不利应力云图；图17～28分别给出S1=60 m、S2=36 m时，不同矢高的凯威特—肋环杂交型椭球面网壳与肋环型椭球面网壳受力位移云图和最不利应力云图。表3给出单一型椭球面网壳与杂交型椭球面网壳受力性能分析与结构性能比对结果。

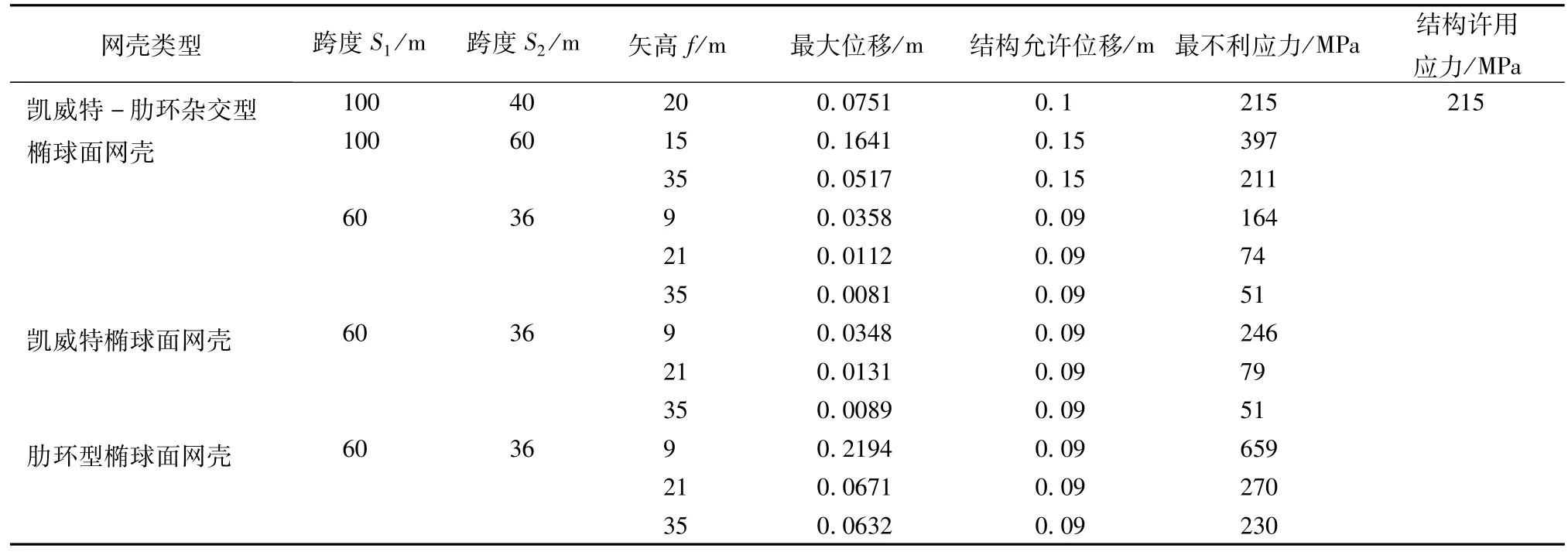
表3 单一型椭球面网壳与杂交型椭球面网壳受力性能分析与结构性能比对

图13 凯威特—肋环杂交型椭球面网壳位移云图（S1=100 m、S2=60 m、f=15 m）

图14 凯威特—肋环杂交型椭球面网壳最不利应力云图（S1=100 m、S2=60 m、f=15 m）

图15 凯威特—肋环杂交型椭球面网壳位移云图（S1=100 m、S2=40 m、f=20 m）

图16 凯威特—肋环杂交型椭球面网壳最不利应力云图（S1=100 m、S2=40 m、f=20 m）

图17 凯威特—肋环型椭球面网壳位移云图（S1=60 m、S2=36 m、f=9 m）

图18 凯威特—肋环型椭球面网壳最不利应力云图（S1=60 m、S2=36 m、f=9 m）

图19 凯威特—肋环型椭球面网壳位移云图（S1=60 m、S2=36 m、f=21 m）

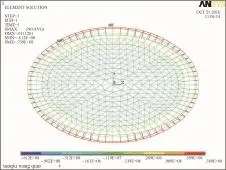
图20 凯威特—肋环型椭球面网壳最不利应力云图（S1=60 m、S2=36 m、f=21 m）

图21 凯威特—肋环型椭球面网壳位移云图（S1=60 m、S2=36 m、f=35 m）

图22 凯威特—肋环型椭球面网壳最不利应力云图（S1=60 m、S2=36 m、f=35 m）

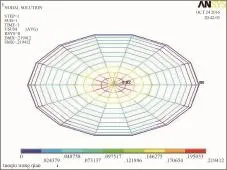
图23 肋环型椭球面网壳位移云图（S1=60 m、S2=36 m、f=9 m）

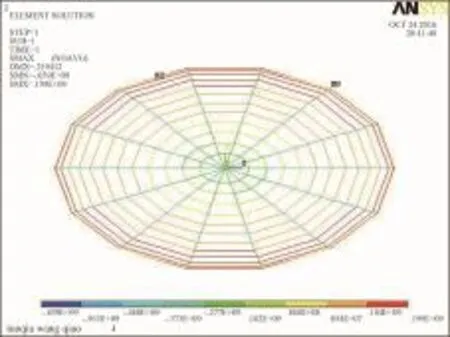
图24 肋环型椭球面网壳最不利应力云图（S1=60 m、S2=36 m、f=9 m）

图25 肋环型椭球面网壳位移云图（S1=60 m、S2=36 m、f=21 m）

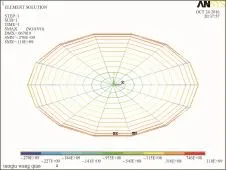
图26 肋环型椭球面网壳最不利应力云图（S1=60 m、S2=36 m、f=21 m）

图27 肋环型椭球面网壳位移云图（S1=60 m、S2=36 m、f=35 m）

图28 肋环型椭球面网壳最不利应力云图（S1=60 m、S2=36 m、f=35 m）

综合分析图13～28和表3可知，相同工况条件下，凯威特—肋环杂交型椭球面网壳跨度和矢高比单一肋环型椭球面网壳和凯威特椭球面网壳有所提高；当长跨为100 m，短跨为40 m，矢跨比为0．5时，杂交型椭球面仍能够满足结构强度和刚度要求，且应力、位移分布均匀；凯威特椭球面网壳强度和刚度优于肋环型椭球面网壳，且应力、位移分布相对均匀。

4 结论

通过上述研究可知：

（1）凯威特—肋环杂交型椭球面网壳，在多种工况下顶点附近应力和位移均较小、且分布均匀，避免了单一网壳类型顶点附近应力集中现象。同等工况下，其受力性能优于单一类型凯威特、肋环型椭球面网壳。

（2）凯威特—肋环杂交型椭球面网壳结构受力（2．35 N/m2）后的最大位移和最不利应力随跨度的增加而逐渐增大，当跨度S1≥110 m时，两类结构（Kn=6、Kn=8）的最不利应力均超过许用应力，故工程中建议单层凯威特肋环杂交型椭球面网壳跨度上限为90～100 m。

参考文献：

［1］ 鹿晓阳，赵晓伟，陈世英.离散变量网壳结构优化设计［M］.北京：中国建筑工业出版社，2013.

［2］ 张志宏，李志强，董石麟.杂交空间结构形状确定问题的探讨［J］.工程力学，2010，27（11）：56-62.

［3］ 张爱林，葛家琪，刘学春.2008奥运会羽毛球馆大跨度新型弦支穹顶结构体系的优化设计选定［J］.建筑结构学报，2007，28（6）：1-9.

［4］ 王澈泉，申波，马克俭，等.正三角形立体管桁架与单层柱面网壳杂交结构的设计与分析［J］.工业建筑，2014，44（6）：130-134，149.

［5］ 王毅，王雪生，朱忠义，等.中国石油大学（青岛校区）体育馆主馆屋盖结构选型与研究［J］.建筑结构，2009，39（12）：71-73.

［6］ 鹿少博.被动优先的绿色实验楼建筑设计探析——以山东建筑大学教学实验综合楼方案设计为例［D］.济南：山东建筑大学，2015.

［7］ 苏亚，鹿少博，鹿晓阳，等.杂交型马鞍网壳结构参数化设计及形状优化［J］.山东建筑大学学报，2016，31（1）：38-46.

［8］ 龚曙光，谢桂兰，黄云清.ANSYS参数化编程与命令手册［M］.北京：机械工业出版社，2009.

［9］ 安然.椭圆水平投影双曲抛物面网壳参数化设计及抗震性能分析［D］.济南：山东建筑大学，2015.

［10］李龙，鹿少博，鹿晓阳，等.大矢高脊线式叉筒网壳静力及抗震性能分析［J］.科学技术与工程，2016，16（14）：268-275，287.

［11］陈亚若，鹿少博，鹿晓阳，等.传统建筑风格与现代网壳结构的融合——四坡与双坡坡屋顶折板网壳参数化设计与受力分析［J］.山东建筑大学学报，2014，29（1）：33-39.

［12］陈世英，鹿晓阳，綦文，等.凯威特网壳最优网格研究［J］.建筑钢结构进展，2013，15（2）：21-25.

［13］辛静，鹿晓阳.单层椭球面网壳的参数化设计［J］.低温建筑技术，2014，36（12）：53-55.

［14］Lu X.Y.，Xin J.，An R.，et al..Ellipsoid reticulated shell of parametric design and analysis ofmechanical characteristics［J］. Applied Mechanics and Materials，2015（716-717）：682-685.

［15］GB 50009—2012，建筑结构荷载规范［S］.北京：中国建筑工业出版社，2012.

［16］JGJ7—2010，空间网格结构技术规程［S］.北京：中国建筑工业出版社，2010.

（校庆约稿）

山东建筑大学工程力学学科——鹿晓阳教授

鹿晓阳教授现为二级教授，享受国务院政府特贴专家、全国优秀教师、山东大学和中国石油大学（华东）博士生导师、山东建筑大学结构工程、工程力学、固体力学和材料加工工程学科硕士导师及国家百千万人才、山东省中青年突贡专家，山东建筑大学工程力学学科首席岗。

鹿晓阳教授博士毕业于清华大学工程力学专业，曾应邀赴美国麻省理工学院、日本东京大学和大阪大学做高级访问学者或研究学者。现兼任全国工科院校力学工作委员会副主任委员、山东省计算力学委员会主任委员。

多年来从事结构优化设计理论与方法和材料加工新工艺及优化设计等研究。2009年和2014年获山东省高等教育教学成果一等奖各一项（均为首位）；主持国家自然科学基金项目四项，研究成果收入“国家自然科学基金优秀成果汇编”；曾获国家科技进步二等奖、教育部技术发明一等奖等省部级以上科研奖励8项（均为首位）；出版学术专著《离散变量网壳结构优化设计》（中国建筑工业出版社，2013年），填补了国内外网壳结构优化设计专著和教材等方面的空白。

Parametric design and stability analysis of hybrid ellipsoid reticulated shell

Lu Xiaoyang1，Fu Haoxin2，Zhao Xiaowei1，et al．

（1.Research Institute of Engineering Mechanics，Shandong Jianzhu University，Jinan 250101，China；2.School of Civil Engineering，Shandong Jianzhu University，Jinan 250101，China）

Hybrid ellipsoid reticulated shell can overcome the shortcomings like the increase of the traditional single ellipsoidal and spherical reticulated shellwith the span of Sand the number of copies of the Knring，the construction difficulty by the increase of rod structure vertex number，and great changes of bar type and scale，thus improving the rationality of the structure and mechanical properties of the structure.According to the characteristics of hybrid ellipsoid reticulated shell，by using APDL（Ansys Parametric Design Language）language，the paper designed ofmacro parameters of hybrid ellipsoid reticulated shell program.By taking Kewitte-rib ring hybrid ellipsoid reticulated shell as an example，and using ANSYS software，it analyzed its mechanical properties.The results show that under the same condition，the rib ring near the hybrid ellipsoid shell vertex displacement and stress are smaller and more evenly distributed，avoiding the single shell type vertex near the stress concentration phenomenon.Itsmechanical performance is better than that of the single type，Kiewittribbed ellipsoid reticulated shell.Kewitte-rib ring hybrid Ellipsoid Reticulated shell the structural stress（2.35 Kn/m2）after themaximum displacement and themost disadvantageous stress gradually increases with the increase of span.Themost unfavorable stress（S1spanmore than 110 m，Kn=6，Kn=8）exceeds the allowable stress，and the engineering advice span limit is 90～100 m.

hybrid type ellipsoid reticulated shell；parametric design；mechanical performance analysis

TU393.3；TU311.41

A

1673-7644（2016）06-0511-10

2016-10-10

国家自然科学基金项目（11272188）；山东省研究生创新计划项目（SDYY08038）；山东建筑大学研究生优质课程资助项目（YZKC201605）

鹿晓阳（1955-），男，教授，博士，主要从事结构优化设计理论方法与受力性能分析、材料加工新工艺及优化设计等方面研究. E-mail：luxy5504@163.com