一类不确定非线性系统的鲁棒调节控制
王继忠,于江波,张长学
(山东建筑大学理学院,山东济南250101)
一类不确定非线性系统的鲁棒调节控制
王继忠,于江波,张长学
(山东建筑大学理学院,山东济南250101)
非线性不确定系统的调节控制是鲁棒控制理论的重要内容。文章研究一类带有未建模动态的控制系数完全未知的不确定非线性系统的鲁棒调节控制问题,应用改变供能函数率的方法、Nussbaum函数增益及局部小增益型条件,提出了鲁棒调节控制方案;分析了其稳定性;并对所提出的鲁棒调节控制方案进行了仿真验证。结果表明:所提出的控制方案对未建模动态、不确定非线性及时变未知控制系数具有良好的鲁棒性;应用改变供能函数率的方法能够克服未建模动态子系统可能导致的系统不稳定性;Nussbaum函数增益能够有效处理控制方向未知、时变的未知控制系数等严重的系统不确定性;局部小增益型条件可以有效解决不可测状态不确定性的增长问题。
鲁棒调节控制;不确定非线性系统;Nussbaum函数;局部小增益条件
0 引言
近年来,关于具有输入状态稳定(ISS)或积分输入状态稳定(iISS)动态不确定性的非线性系统的反馈控制研究是控制理论研究的热点问题之一[1]。输入状态稳定性是对关于最大值范数的有限增益和有限L2增益(“非线性H∞”)的一种非线性推广;该属性考察了初始状态在某种意义上与经典Lyapunov理论完全相容,并且用非线性增益取代了对一般非线性控制要求过高的有限线性增益。当被一致有界的能量信号所激励时,一个ISS系统表明了低的能量响应[2-3]。积分输入状态稳定(iISS)是输入状态稳定(ISS)的积分变形,是比输入状态稳定(ISS)更弱的一类稳定性[4-7]。该性质定性反映了当干扰具有有限能量时小的超调并为线性系统提供了一个类似有限H2范数的定性结论,具有重要的物理意义。ISS及iISS的出现,使得系统不确定性更加广泛。借助于ISS及iISS方法,系统的动态不确定性可以是非线性的,对于动态不确定性需要满足线性的最小相位条件有了很大改进[8]。
控制系数未知是系统存在的另一种严重的不确定性,与控制系数已知情形相比,控制系数未知使得传统的Backstepping设计方法不再适用,导致控制器设计极为困难,现有结果通常假设未知的控制系数上下界已知[9-13]。Nussbaum首次提出基于Nussbaum增益的设计技术[14],该方法是处理虚拟控制系数完全未知时的系统控制问题的一种非常有效的工具[2]。文章应用Nussbaum增益技术,结合积分器反推方法,研究一类带有未建模动态的控制系数完全未知的不确定非线性系统的鲁棒调节控制问题,得到的结论进一步推广了现有结果[6-7]。
1 鲁棒调节控制问题描述

研究一类如式(1)所示的不确定非线性系统的鲁棒调节控制问题。式中:u,y∈R是系统输入及输出;ω∈Rr代表系统的动态不确定性;x=(x1,…,xn)∈Rn是系统状态;φi(ω,y,d(t)) 是未知的不确定函数,代表未建模动态;bi(t)是大小及符号未知的控制系数。
研究目标是设计控制律u,使得系统状态(ω(t),x1(t),…,xn(t)) 在时间t趋于无穷大时收敛到零。为实现这一目标,对于式(1)为

式中:γ0(s)=O( s2)。
假设2 存在非负光滑函数φi1、φi2(i=1,…,n)及pij≥0(i=1,…,n;j=1,2),使得满足式(3)所示条件。
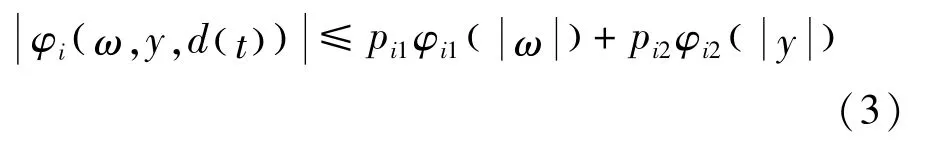
式中:φi1满足式(4)所示局部小增益型条件。

2 鲁棒调节控制器设计
应用Backstepping方法系统地给出鲁棒调节控制器的设计过程。
第1步 对于x1-子系统,记z1=x1,选取李亚普诺夫函数由式(5)表示为

根据假设1及假设2,存在光滑函数γ^(x1)≥0,使得式(5)的导数满足式(6)为应用完全平方公式,对于不确定项p11φ11(ω)z1,满足式(7)为
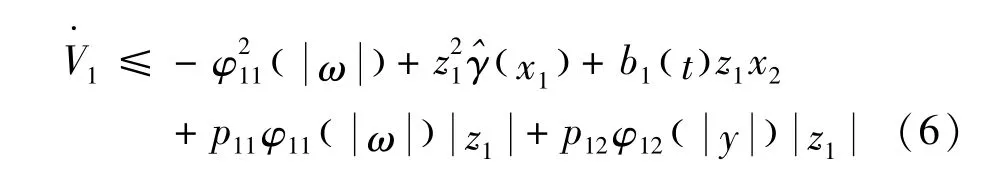

由 φ12(0)=0,可以进一步得到
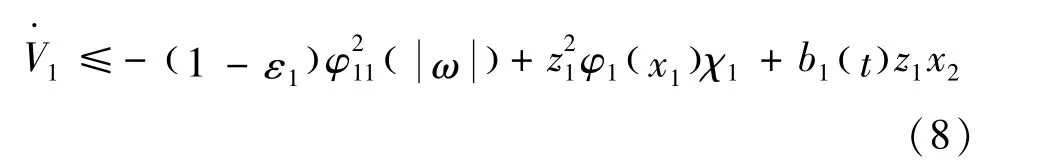
记z2=x2-ϑ1,其中ϑ1为虚拟控制律,则式(8)转化成式(9)表示为

将式(10)代入式(9)中得式(11)为


第k( 2≤k≤n-1)步假设已设计虚拟控制律及动态光滑函数,由式(13)表示为

使得正定正则可微的李亚普诺夫函数,由式(14)表示为

且式(14)的导数满足
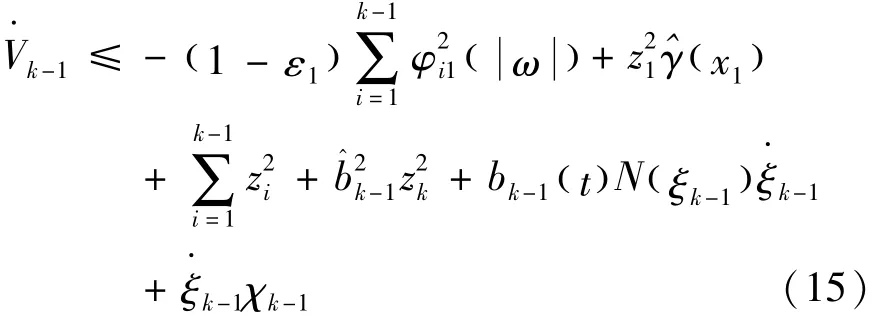
以下证明式(15)对于第k步也成立。选取李亚普诺夫函数,由式(16)表示为
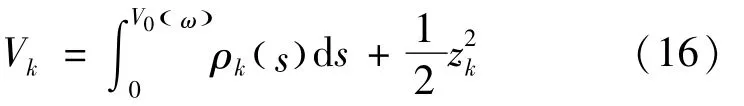

可以验证式(16)导数满足式(17)为与第1步类似,对式(17)中的不确定项,应用完全 平方公式,得到式(18)~(20)为

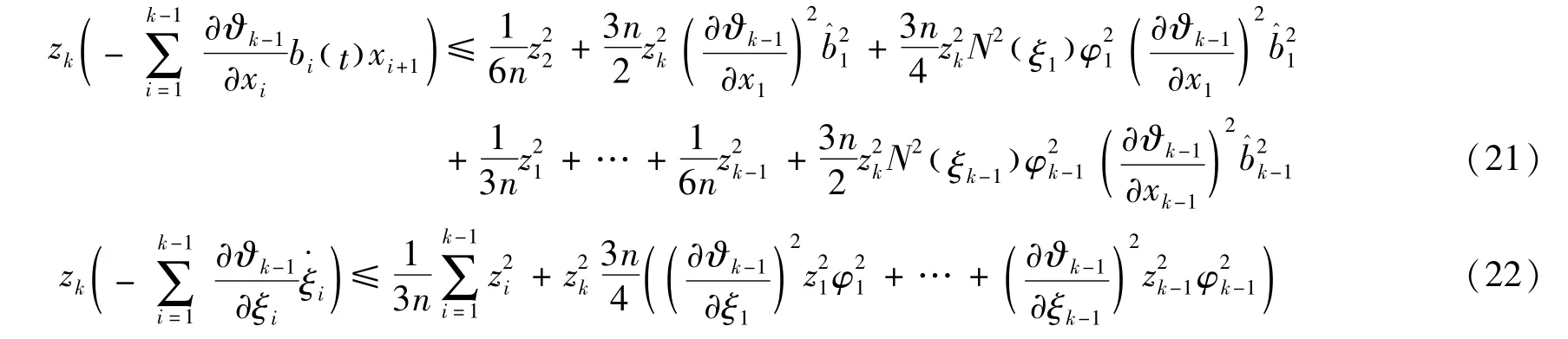
选取函数φk( x1,…,xk,ξ1,…,ξk-1)及χk=因此,把式(18)~(22)代入式(17),得到式(23)为
选取第k个虚拟控制律及动态增益由式(24)表示为

于是,式(23)变为式(25)为

第n步选取李亚普诺夫函数由式(26)表示为

式(26)的导数满足式(27)为

选取控制律及动态增益由式(28)表示为

结合式(27)得到式(29)为

至此,结合Nussbaum增益的反步法,研究给出了由式(1)表示的不确定系统的鲁棒控制器设计。
3 鲁棒稳定性分析
假设闭环系统解的最大存在区间是 [ 0,tf)。对k=1,…,n,选取恰当的εk>0,式(25)可以进一步由式(30)表示为
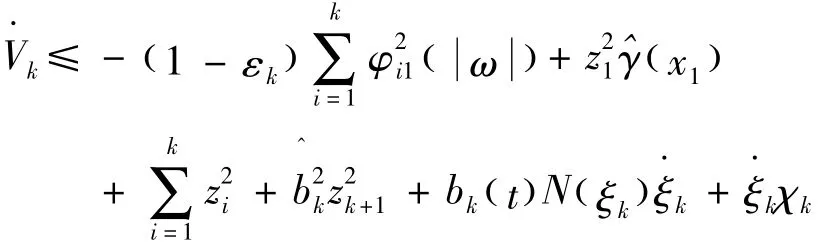

进一步可以得到,ξk(t)( 1≤k≤n)在 [ 0,tf)上有界。根据Vk(t)( 1≤k≤n)的定义,其在 [ 0,tf)上有界,进一步的,ω(t)与zk(t)( 1≤k≤n)有界。考虑到xk=zk+αk-1( 1≤k≤n),可以得到xk(t)有界。因此,闭环系统信号在 [ 0,tf)上有界,因此tf=∞。考虑到 ( ω,x)的有界性,可以得到致连续。根据ξk有界,可得式(31)为

由Barbalat引理[15],得到
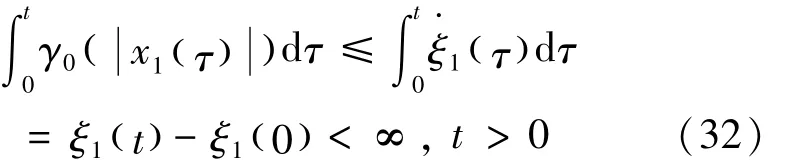
从而得到如下结论:若假设1~3成立,则闭环系统的解在 [ 0,∞ )上有定义且有界。特别的,系统状态收敛到零,由式(33)表示为

4 仿真实验
文章对提出的控制方案进行仿真验证。考虑如下系统,由式(34)表示为



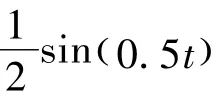
选取b1(t)=及初始条件ω(0)=0.5,x(0)= ( 1,0),ξ(0)=( 0.5,1),绘制了闭环系统的状态—时间响应图、控制输入变量—时间响应图,分别如图1(a)、1(b)所示。从图1所示的系统状态及控制输入与时间的响应图可以看出,该控制方案对未建模动态及时变未知控制系数具有良好的鲁棒性。
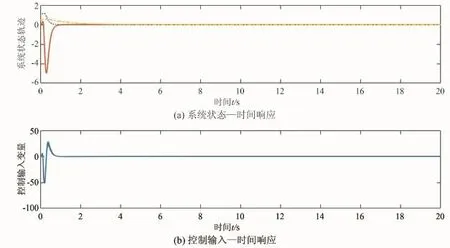
图1 系统状态及控制输入与时间的响应图
5 结论
根据以上分析可知:
(1)提出的控制方案对未建模动态、不确定非线性及未知的控制系数具有良好的鲁棒性,能够实现所研究的不确定非线性系统的鲁棒调节控制问题。
(2)应用改变供能函数率的方法可以克服积分输入状态稳定(iISS)的未建模动态子系统可能导致的系统不稳定的影响。
(3)Nussbaum函数增益通过产生一类不依赖于控制系数的符号的振荡信号,能够有效处理控制方向未知、时变的未知控制系数等严重的系统不确定性。
(4)局部小增益型条件建立了系统非线性与未建模动态子系统供能函数率间的联系,可以有效解决不可测状态不确定性的增长问题。
[1] Karafyllis I.,Jiang Z.P..Stability and Stabilization of Nonlinear Systems[M].London:Springer,2011.
[2] Jiang Z.P.,Mareels I.,Hill D.J.,etal..A unifying framework for global regulation via nonlinear output feedback:From ISS to iISS[J].IEEE Transactions on Automatic Control,2004,49(4):549-562.
[3] Ito H.A..Lyapunov approach to cascade interconnection of integral Input-to-State stable systems[J].IEEE Transactions on Automatic Control,2010,55(3):702-708.
[4] 段纳,王璐,赵丛然.一类具有积分输入到状态稳定未建模动态的高阶非线性系统的状态反馈调节[J].控制理论与应用,2011,28(5):639-644.
[5] 赵丛然,解学军.具有iISS逆动态的非线性系统的输出反馈调节[J].自动化学报,2012,38(5):865-869.
[6] Yu J.B.,Wang J.Z.,Zhang C.X.,et al..Output feedback regulation control for a class of uncertain nonlinear systems[J]. Journal of Dynamic SystemsMeasurement and Control-Transactions of the ASME,2015,137(4):1-5.
[7] 赵彦,于江波,田洁.一类非线性系统的输出反馈跟踪控制[J].系统科学与数学,2014,34(7):853-861.
[8] 杨强,刘玉生.不确定非线性系统的鲁棒自适应输出反馈控制[J].控制与决策,2015,30(6):993-999.
[9] 刘允刚.增长率为输出的未知多项式非线性系统的全局输出反馈跟踪[J].控制理论与应用,2014,31(7):921-933.
[10]闫雪华,刘允刚.一类具有未知增长率非线性系统全局输出反馈实际跟踪[J].中国科学(信息科学),2011,41(6):704-715.
[11]王金诚.具有未知控制系数随机系统的状态反馈镇定[J].控制工程,2016,23(1):109-112.
[12]陈彭年,秦化淑,方学毅.控制增益时变的非线性系统的迭代学习控制[J].系统科学与数学,2012,32(6):693-704.
[13]赵平,刘淑君.一类虚拟控制系数未知的随机非线性时滞大系统的适应镇定控制[J].自动化学报,2008,34(8):912-920.
[14]Nussbaum R.D..Some remarks on a conjecture in parameter adaptive control[J].Systems&Control Letters,1983,3(5):243 -246.
[15]Krstic M.,Kanellakopoulos I.,Kokotovic P.V..Nonlinear and Adaptive Control Design[M].New York:Wiley-Interscience,1995.
(校庆约稿)
山东建筑大学数学学科——王继忠教授

王继忠教授现为山东建筑大学重点岗教授、山东省教学名师,硕士生导师,校级重点学科“应用数学”学科带头人。
王继忠教授博士毕业于西安电子科技大学应用数学专业,2008年3月至2016年5月间曾担任理学院院长。现兼任应用数学研究所所长、山东省专业教学指导委员会委员、山东省高等数学学会副理事长。
多年来一直在高校从事教学和管理工作,主要从事微分方程的稳定性、有界性的研究和控制系统绝对稳定性的研究,先后为本科生和研究生主讲了《数学分析》、《实变函数》等九门课程,取得了良好的教学效果;主持山东省面向二十一世纪教学改革课题一项、科研课题一项;承担山东省自然科学基金课题一项,作为主要成员参与国家自然科学基金课题3项;出版学术专著一部;发表论文30余篇,其中,三大检索收录11篇。先后荣获临沂市十大杰出青年、劳动模范、专业技术拔尖人才、山东省第五届青年科技奖、山东省优秀教学成果一等奖。
Robust regulation control for a class of uncertain nonlinear system s
Wang Jizhong,Yu Jiangbo,Zhang Changxue
(School of Science,Shandong Jianzhu University,Jinan 250101,China)
The regulation control for the nonlinear uncertain systems is a central topic in robust control theory.This paper studies the robust regulation control problem for a class of nonlinear uncertain systems with unmodeled dynamics,uncertain nonlinearities,and unknown time-varying control coefficients.A robust regulation control scheme is presented using the changing supply rates technique,Nussbaum function gain as well as local small-gain conditions,and then the stability is analyzed.The simulation example verifies its efficacy.The results show that he proposed control scheme is robust against the unmodeled dynamics,uncertain nonlinearities,and unknown control coefficients;the changing supply rates technique could overcome the possible instability because of the unmodeled dynamic subsystem;Nussbaum function gain could effectively handle serious uncertainties in systems such as the unknown control direction,time-varying unknown control coefficients and so on;local small-gain conditions could well address the unmeasured states growth problems.
robust regulation control;uncertain nonlinear systems;Nussbaum function;local smallgain conditions
93D15
A
1673-7644(2016)06-0593-06
2016-11-11
国家自然科学基金项目(61304008);山东省优秀中青年科学家科研奖励基金项目(2015BSB01450);山东建筑大学博士基金项目(XNBS1272)
王继忠(1959-),男,教授,博士,主要从事微分方程定性理论及在控制理论中的应用等方面的研究.E-mail:wjz600265@163.com

