表面效应对压电纳米梁弯曲行为的影响

杨 帆

（1. 西安科技大学 理学院，陕西 西安 710054；2. 西安交通大学 工程力学系，陕西 西安 710049）

表面效应对压电纳米梁弯曲行为的影响

杨 帆1,2

（1. 西安科技大学 理学院，陕西 西安 710054；2. 西安交通大学 工程力学系，陕西 西安 710049）

基于Euler-Bernouli模型，分析了表面效应对压电纳米梁弯曲行为的影响。基于表面弹性理论和“核壳”模型，采用表面能模型引入表面效应的影响。通过最小势能原理建立起包含表面效应及压电效应的压电纳米梁弯曲行为的控制方程和边界条件。讨论了表面效应对氧化锌悬臂梁结构的压电纳米梁弯曲变形及其产生的感应电荷的影响。结果表明，表面效应使得压电纳米梁的弯曲变形变小，感应电荷量减少。这些结论对设计、校正和测量压电纳米梁及其为基础的纳米器件具有重要的指导意义。

表面能；压电纳米梁；能量原理；弯曲变形；感应电荷；ZnO

随着压电材料应用越来越广泛，人们想将其用于低能耗电子产品中，但传统的压电材料都不适合，于是研制纳米级别的压电材料成为前景不错的全新领域。美国亚特兰大佐治亚理工学院王中林研究小组实验研究分析，用竖直结构的ZnO纳米线把机械能转化为电能的过程，发现ZnO纳米线具有半导体性能和压电效应，用导电的原子力显微镜探针针尖去弯曲竖直生长的ZnO纳米线，使ZnO纳米线的内部和外部分别发生压缩和拉伸变形，从而导致弯曲的ZnO纳米线的内外表面产生正负极化电荷，并借助其半导体性质和其金属尖部的肖特基势垒将电荷暂时存储在体内，然后用导电的原子力显微镜探针接通，向外界输电以实现在纳米尺度上把力学能转化为电能。该研究小组表示该纳米发电机的发电效率可以达到17%～30%，并提出自激励纳米装置的概念[1-2]。

王刚锋与冯西桥基于Euler-Bernouli梁模型研究了残余表面应力对压电纳米线的振动与屈曲行为的影响[3]。利用有限元方法，Kim等[4]提出了一个理论模型以计算具有尺度效应的ZnO线/梁的等效压电系数。利用梁弯曲模型，Wang等[5]分析了表面效应及小尺寸效应对压电纳米线机电耦合性能的影响，推导了问题的控制方程。利用分子动力学“核壳”模型[6]，机、电耦合作用下压电纳米线的力学行为也得到了理论研究。

压电纳米问题主要从材料方向和微电子方向研究压电势能的比较多，主要研究其材料、物理性能。研究的结构包括有纳米管、纳米线、纳米带、纳米须晶、纳米层合结构，主要是ZnO材料，也有BaTiO3。目前，考虑表面效应的纳米压电力学问题还比较少。本文基于表面弹性理论和“核壳”模型，采用表面能模型引入表面效应的影响，分析了氧化锌纳米梁在压电效应及表面效应下的线性弯曲行为。用最小势能原理推导了计及压电效应及表面效应的压电纳米梁弯曲控制方程及边界条件并求解。同时还计算了压电纳米梁弯曲变形产生的感应电荷，分析了感应电荷与压电纳米梁弯曲变形程度的关系。

1 压电纳米梁弯曲的基本方程

考虑如图1所示的压电纳米梁在横向载荷F作用下线性弯曲情况。坐标轴y、z方向如图所示，u和w分别为压电纳米梁上任一点在坐标轴y、z上的位移。根据文献[7-8]，压电纳米梁在发生弯曲变形后，受压的一面产生负电荷，受拉的一面产生正电荷。图1所示压电纳米梁在载荷F作用下，上表面受压，产生负电荷，下表面受拉，产生正电荷。

图1 压电纳米线及其横截面形状Fig.1 Piezoelectric nanowire & cross section

采用Euler-Bernoulli梁模型，考虑到压电纳米梁在外载荷作用下为线性弯曲，则由几何线性关系，梁上任意一点的应变为

对于一维压电纳米梁结构，压电梁的应力应变关系如下

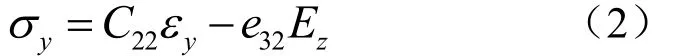
式中：C为压电材料的刚度系数；e为压电材料的压电常数；E为电场强度矩阵。

对于一维压电纳米梁结构，由电磁学理论，电位移公式为

式中：D为压电材料的电位移；λ为压电材料的介电常数；Φ为电势。

一维压电纳米梁结构中，y轴方向上的电场强度远小于z轴方向上的电场强度，即Ey＜＜Ez，则y轴方向上的电位移Dy相对于z轴方向上的电位移Dz可忽略不计。

由电学平衡方程

将公式(1)、(2)和(3)代入公式(4)中，得到如下形式方程

式中：a1，a2为待定系数。

2 表面效应对压电纳米梁弯曲的影响

对于表面效应的表征有残余表面应力及表面能两种形式。在本文中采用表面能模型计及表面效应的影响。在能量模型下，表面效应对构件力学行为的影响可通过表面能来表征并引入计算中。

基于表面弹性理论和“核壳”模型，认为表面是一个可以忽略厚度的薄膜如图1(b)所示，纳米梁横截面表面薄膜厚度ts远远小于梁横截面高t与宽度b。对于线性弯曲变形的压电纳米梁，表面效应对弯曲刚度的影响同样可用等效弯曲刚度(EI)*及等效拉压刚度(EA)*来计算，其式为[9-10]

式中：Es为表面弹性模量，其值可以通过分子模拟或实验[11]测得；E为梁体内部的弹性模量。

表面能为由固体自由表面产生的额外自由能。因此，固体变形后会增加新表面积，从而需要外力做功，这部分能量也应包含在总能量中。为了简便，这里假设表面能密度γ在整个梁表面为一常数，则整个压电纳米梁的表面能US可表示为[12]

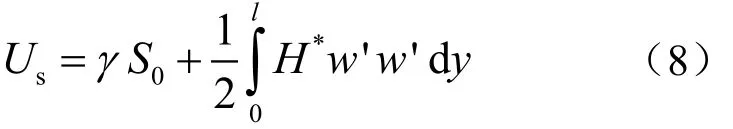
式中：S0为梁变形前的表面积，对于矩形横截面梁其大小为2(b+t)l，对于圆形横截面梁为πDl；H*为与梁横截面相关的常数，对于矩形横截面其大小为2γ(b+t)，对于圆形横截面为πDγ。

压电纳米梁上的应变能Ub

假设压电纳米梁上受到分布载荷q(y)及端部外载荷F作用，外力势能V有如下表达式

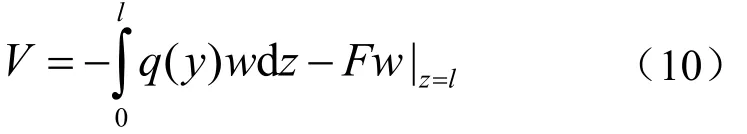
及边界条件

利用公式(11)，联立边界条件公式(12)可计算考虑表面效应时压电纳米线的弯曲挠度。对于如图1所示的压电纳米悬臂梁结构其边界条件为

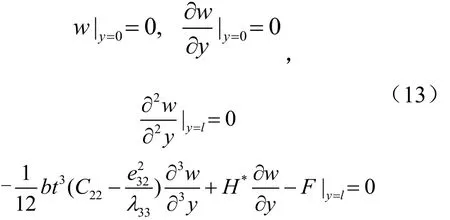
微分控制方程(11)联合边界条件公式(13)即可计算得计及表面效应的压电纳米梁弯曲变形挠度。当表面能密度γ=0与表面弹性模量Es=0时，微分控制方程(11)和边界条件公式(12)退化为无表面效应的经典理论下普通压电梁的问题，即可求出普通压电梁的弯曲问题。

压电纳米梁上下表面可视为两平行电板，压电纳米梁弯曲变形后产生的感应电荷，根据电磁学理论有以下关系式

式中：C为电容。

有电容计算公式

式中：S为电容器板的面积；d为电容器板间距离；ε0为介电常数。

故有

将公式(5)、(16)代入公式(14)，且考虑到感应电荷产生于压电纳米的表面上，得到以下结果

当压电纳米梁横向挠度w=0时，感应电荷Q=0，则待定系数a1=0，公式(17)可简化为

3 结果及讨论

为方便计算，引入以下无量纲量代入计算：

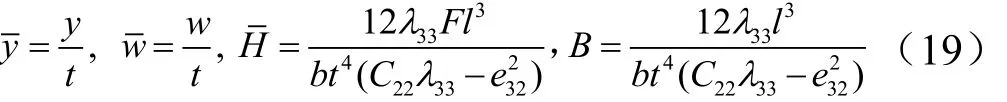
式中：B为无量纲参数。计算过程中压电纳米梁的物理参数如表1所示。

表1 压电纳米梁的物理参数[4]Tab.1 Material parameters of piezoelectric nanowire

考虑横截面高t=20 nm，宽b=20 nm，长l=400 nm的压电纳米梁。图2为外载荷F=80 nN时，压电纳米梁的弯曲构型图。从图中可以看到，当受到同样大小的外载荷时，考虑表面效应的纳米压电梁的弯曲变形比忽略表面效应的压电梁弯曲变形小。表面效应使得压电梁刚度增强。

图2 压电纳米梁在外载荷F=80 nN时弯曲构型图Fig.2 Deflection of the piezoelectric nanowire (F=80 nN)

图3为无量纲载荷F/B与压电纳米梁最大变形处，即压电纳米梁的自由端无量纲横向挠度w/t关系图。随着外载荷的增加，压电纳米梁的自由端无量纲横向挠度增加。计及表面效应的压电纳米梁与忽略表面效应的经典理论结果相比，在相同变形程度下，压电纳米梁需要更大的外载荷。表面效应使得压电纳米梁弯曲变形更小，梁的刚度增加。

图3 无量纲载荷与压电纳米梁自由端横向挠度曲线Fig.3 The variation of tip deflection with load

图4为无量纲外载荷F/B与压电纳米梁由于变形而产生的感应电荷的关系图。随着从无量纲外载荷F/B的增加，压电纳米梁由于变形而产生的感应电荷量增加。从图中可以明显看到，对于相同的外载荷，考虑表面效应的压电纳米梁产生的感应电荷比不考虑表面效应的普通压电梁产生的电荷少。这是因为对应相同的外载荷，压电纳米梁的弯曲变形比不考虑表面效应的普通压电梁的弯曲变形更小，导致产生的感应电荷也更少，这与图3所示的结论相吻合。

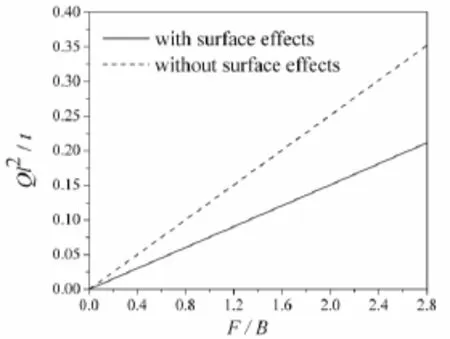
图4 无量纲载荷与感应电荷关系图Fig.4 The varitaion of induced charge with load

4 结论

在压电纳米材料的逐渐应用下，对带压电效应的纳米梁弯曲问题分析就显得意义重大。本文基于表面弹性理论和“核壳”模型，采用表面能模型引入表面效应的影响，分析了氧化锌纳米梁在压电效应及表面效应下的线性弯曲行为。用最小势能原理推导了计及压电效应及表面效应的纳米梁弯曲控制方程及边界条件，并对控制方程结合边界条件进行求解。同时还计算了压电纳米梁产生的感应电荷。具体分析了一个悬臂梁结构的压电纳米梁的线性弯曲。计算结果表明，表面效应使得压电纳米梁弯曲变形减小，梁的刚度增加，由变形产生的感应电荷减小。表面效应对压电纳米梁的力学行为有着显著的影响。这些结论对设计、校正和测量压电纳米梁及其为基础的纳米器件具有重要的指导意义。

[1] BAI X D, WANG E G, GAO P X, et al. Measuring the work function at a nanbelt tip and at a nanoparticle surface [J]. Nano Lett, 2003, 3(8):1147-1150.

[2] WANG Z L. Towards self-powerd nanosystems: from nanogenerators to nanopizotronics [J]. Adv Funct Mater, 2008, 18: 1-15.

[3] WANG G F, FENG X Q. Effect of surface stresses on the vibration and buckling of piezoelectric nanowires [J]. Europhys Lett, 2010, 91(5): 56007-1-4.

[4] KIM S M, SOH J I, KIM H J, et al. Radially dependent effective piezoelectric coefficient and enhanced piezoelectric potential due to geometrical stress confinement in ZnO nanowires/nanotubes [J]. Appl Phys Lett, 2012, 101(1): 013104-1-3.

[5] WANG K F, WANG B L. The electomechanical coupling behavior of piezoelectric nanowires: surface and small-scale effects [J]. Europhys Lett, 2012, 97: 66005-1-6.

[6] ZHANG Y H, LIU B, FANG D N. Stress-induced phase transition and deformation behavior of BaTiO3nanowires [J]. J Appl Phys, 2011, 110(5): 054109-1-5.

[7] ZHOU J, LAO C S, GAO P X, et al. Nanowires as pico-gram balance at workplace atmosphere [J]. Solid State Commun, 2006, 139: 222-226.

[8] ZHOU J, WANG Z L, GROTS A, et al. Electric field drives the nonlinear resonance of a piezoelectric nanowire [J]. Solid State Commun, 2007, 144: 118-123.

[9] MILLER R E, SHENOY V B. Size-dependent elastic properties of nanosized structural elements [J]. Nanotechnology, 2000, 11(3): 139-147.

[10] WANG G F, FENG X Q. Effects of surface elasticity and residual surface tension on the natural frequency of microbeams [J]. Appl Phys Lett, 2007, 90(23): 231904-1-3.

[11] WANG G F, FENG X Q. Surface effects on buckling of nanowires under uniaxial compression [J]. Appl Phys Lett, 2009, 94(14): 141913-1-3.

[12] WANG G F. Effects of surface energy on the mechanical performance of nanosized beams [J]. J Compos Theor Nano, 2011, 8(7): 1173-1177.

（编辑：曾革）

Effect of surface energy on the bending of piezoelectric nanowires

YANG Fan1,2
(1. College of Sciences, Xi’an University of Science and Technology, Xi’an 710054, China; 2. Department of Engineering Mechanics, Xi’an Jiaotong University, Xi’an 710049, China)

The influence of surface energy on the bending of piezoelectric nanowire was analyzed by using the Euler-Bernouli beam model. The effects of surface was considered by surface energy model. Through the principle of minimum potential energy, the influence of surface energy on the bending performance of piezoelectric nanowire was formulated. The governing equation and the boundary conditions were obtained. It is found that the bending deformation and induced charge of piezoelectric nanowire can be decreased by the surface effects. This study is helpful for the design of nanowire-based devices and characterization of the mechanical properties of nanowires.

surface energy; piezoelectric nanowire; energy principle; bending deformation; induced charge; ZnO

10.14106/j.cnki.1001-2028.2016.08.011

TN303

:A

:1001-2028（2016）08-0046-04

2016-05-12

国家自然科学基金项目（No. 11502197）；陕西省博士后项目

杨帆（1981-），女，四川资中人，讲师，博士，研究方向为纳米力学，E-mail: yangfan0832@163.com 。

时间：2016-08-03 22:36

： http://www.cnki.net/kcms/detail/51.1241.TN.20160803.2236.011.html