基于蚁群算法的城市公共自行车调度研究

张辉++郑彭军

摘要：由于城市公共自行车存在供需时空分布的不均衡性，因而进行公共自行车的调度是十分必要的。通过分析现阶段我国城市公共自行车调度方式特性，为充分满足租赁者的需求，提出了一种带模糊时间窗的城市公共自行车调度路径优化模型。以租赁点满意度最大化为目标函数，同时将基本蚁群算法进行改进后应用于求解最优调度路径模型。最后，以宁波市公共自行车区域调度为例，运用Matlab进行仿真实验，证明了该模型及求解算法的有效性和可行性。

关键词：公共自行车调度；蚁群算法；模糊时间窗

DOI：10.16315/j.stm.2015.06.006

中图分类号：U491.1+7

文献标志码：A

公共自行车系统可有效缓解公共交通末端“最后一公里”出行难题，从而成为城市公共交通的重要辅助形式。然而各城市在逐步推进公共自行车系统建设的同时，也伴随着不少问题，其中共性又极具代表性的是公共自行车的“租还车难”问题。由此引发的公共自行车调度是以满足租赁者的租还需求为目的，为了提高公共自行车周转率的特殊的物流活动。现阶段我国各城市的公共自行车调度工作主要以人工调度为主，信息化水平不高，调度人员多以历史或实时公共自行车租借数据凭主观经验通过巡逻的方式安排车辆调度路径，尚未形成科学系统的调度模式，时效性不高，不乏出现公共自行车车辆到位时租赁者转而选择其他交通方式的现象。

对于城市公共自行车调度，现有的研究主要分为静态跟动态调度两方面。在静态调度方面：刘登涛等以运输成本最小化为目标建立了公共自行车系统的调度模型，并运用模拟退火算法求解该模型，得到了公共自行车系统的静态调度计划。Benchimol[4]和Chemla假设城市公共自行车系统中各租赁点自行车库存量已给定，即在调度需求己知的情况下，以运输费用最小化为目标，进行公共自行车的调度。Gune等研究了公共自行车系统的静态再平衡分配问题，以实现最低调度成本为目标确定调度序列站，由一辆调度车辆将公共自行车收集起来并交付到各个站点。但由于现实中公共自行车的流动性，公共自行车调度问题应隶属动态调控，采用静态模式研究无法更精准的预估结果，研究也具有一定的滞后性。因此衍生出了一系列公共自行车动态调度研究：董红召等针对公共慢行系统中存在的公共自行车在时间和空间上分布不均衡的问题，研究了公共慢行系统调度过程中租赁点需求的动态特性及其模糊时间窗的约束，以最大化租赁点的满意度为目标建立了公共慢行系统调度的模型，动态的获取调度计划，进而实现公共慢行系统的动态调度。Leonardo C提出了一种动态自行车再分配仿真模型，模型的目的在于尽量减少自行车运营商的调度成本，同时兼顾用户满意度。吴满金等对公共自行车调度过程中自助服务点调度的优先级、动态需求特性、服务时间窗等进行了研究，建立了统筹用户满意度与企业调度成本的公共自行车系统动态调度多目标优化模型，并设计了一种禁忌遗传混合算法对动态调度模型进行了求解。张建国等建立了基于滚动时域的公共自行车调度路径优化模型，但该模型没有考虑到装卸自行车的服务时间等对整个调度时间的影响，结果并不完全可靠。

鉴于城市公共自行车调度的时效性，在既有研究的基础上，本文通过构建带模糊时间窗的调度模型，提出了一种区域单调度中心多调度车辆的调度模式，并将基本蚁群算法进行改进后运用于求解该模型，最后通过真实数据进行案例分析，从而验证模型及算法的合理性和科学性。

1 问题分析

城市公共自行车系统通常都具备相应的调度中心，其功能为实时掌握各个公共自行车租赁点的车辆运营状况，一旦租赁点的公共自行车在桩数量未在有效安全阀值以内，一般为租赁点20%-80%的公共自行车在桩率，就该对该租赁点的车辆进行调度，从而避免出现空桩或满桩现象。当然，更完善的调度系统同时具备了预调度功能，即根据历史经验数据对重点观察的租赁点在公共自行车数量未报警时就提前展开调度工作。

根据实际城市公共自行车调度状况，本文所要解决的是带模糊时间窗的公共自行车调度问题：即在某一特定时段，若干个公共自行车租赁点同时产生调度需求时，在现有调度资源有限的情况下，引入时间惩罚的概念，以各个公共自行车租赁点的满意度最大化为目标，调度车在既定的时间窗内将过剩的公共自行车收集起来，合理有效得分配到各个车辆不足的公共自行车租赁点。2模型描述

以公共自行车租赁点满意度最大化为目标函数所建立的调度模型与调度车辆抵达租赁点的调度时间密切相关。在实际公共自行车系统的调度过程中，特别在早晚高峰期间，调度中心都会根据各个租赁点的历史租还车辆数据，在租赁点公共自行车数量未报警时就提前安排调度工作。一旦租赁点的公共自行车数量未在安全阀值以内，各个租赁点更倾向于在一开始即最佳的时间窗内就能接受调度，只有这样才可能百分百得满足租赁者的租还需求。然而在实际调度过程中，在某一特定的时间范围内通常会出现若干个租赁点自行车数量同时报警，由于调度车辆有限部分租赁点很有可能被延迟服务，但在被延迟的这一段时间范围内，由于租赁点自身仍有自行车可以被租赁者租还，起到了缓冲作用，只不过这样租赁点的满意度会随之降低，直到空满桩现象发生满意度才降为零。

为此，本文引入模糊时间的概念，建立带模糊时间窗的车辆调度模型，即调度车未在最佳调度时间窗内抵达租赁点对其进行调度服务时，租赁点的满意度要打个折扣，具体表现在租赁点满意度呈现对应下滑。考虑到租赁者的租还意向对调度时间的要求并不是完全线性的，通常情况下越靠近最佳的调度时间范围，租赁点的满意度流失得越慢，当调度时间超出可接受时间范围，满意度则降为0，

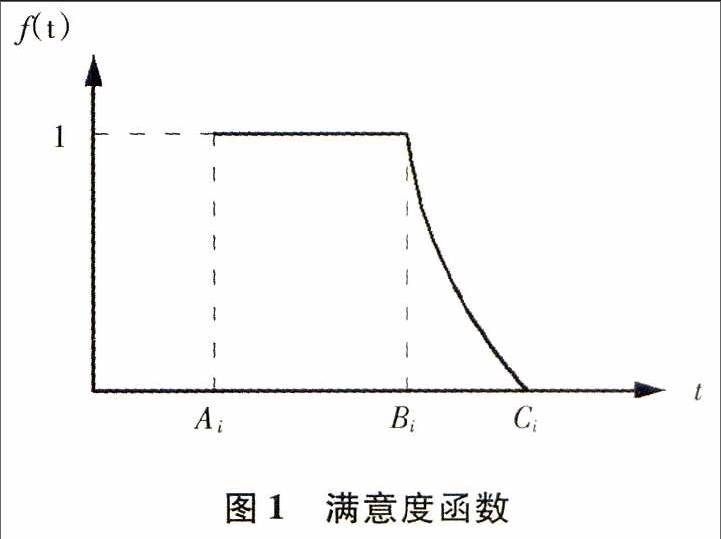
满意度函数是用来衡量租赁点对调度工作的满意程度，也可以从侧面体现租赁者对调度工作的满意程度，如图1所示。

当调度车抵达租赁点ui的时间Ti∈（Ai，Bi）时，即车辆预调度时段，租赁点ui对此次调度服务的满意度fi（Ti）最大，且fi（Ti）=1；当抵达时间Ti∈（Bi，Ci）时，即租赁点车辆数报警并已发出调度需求指令时段，租赁点ui对此次调度服务的满意度fi（T）介于0与ι之间；当抵达时间Ti>Ci时，即租赁点已产生空满桩现象，租赁点ui对此次调度服务的满意度fi（Ti）最小，且fi（Ti）=0。因此，租赁点满意度函数可以表示为式中：0<β<1为租赁点对时间的敏感系数。因此，本文所研究的公共自行车调度的数学模型如下：U={u1，u2，u3，，，un}表示所有公共自行车租赁点的集合，n是所有需要调度公共自行车的租赁点的数目，调度中心为O。租赁点ui需要调度的自行车数量为|di|（0<|di|

目标函数为式中：Z为租赁点满意度；T为时间轴；N（t）为t时刻，所有未被调度的租赁点集合；M（t）为t时刻，所有已调度完成的租赁点集合；tik为调度车k抵达租赁点ui的时间；Qi为调度车在租赁点ui调度完成后车上装载的自行车数量。式（2）是该模型的目标函数，即实现租赁点的满意度最大化；式（4）确保调度车不超载；式（5）确保调度车从调度中心出发完成调度任务后最终都要回到调度中心；式（6）确保每个租赁点有且仅被调度车服务一次。

3 模型求解

带模糊时间窗的城市公共自行车调度路径优化问题是一个多约束非线性组合优化问题，由于受到时间窗的约束，最短调度路径不一定是最优化选择，目前多以启发式算法求解该问题满意解。蚁群算法作为一种基于动物种群的启发式仿生优化算法，由意大利学者Colomi等提出，因其具有良好的并行性、协作性和鲁棒性，寻优特性好，常用于求解VRP模型，但同时也存在搜索时间长、收敛速度慢、易陷于局部最优等缺点。

3.1 基本蚁群算法

1）算法描述。设蚁群中共有m只蚂蚁，将m只蚂蚁放置在调度中心O，用禁忌表tabuk记录当前蚂蚁k（k=l，2，3，…，m）所走过的租赁点，每走过一个租赁点，都需要修改禁忌表，当所有n个租赁点都加入到tabM。中时，蚂蚁k便完成了一次调度任务，此时蚂蚁k所走过租赁点的路径便是该模型的一个可行解。

2）信息素初始化。Tij（t）表示t时刻租赁点ui与租赁点uj之间路径上的信息素浓度。在蚁群算法迭代初期，为减少租赁点间的距离信息对蚂蚁开始搜索的影响，增强蚂蚁初始搜索的随机性，提高蚂蚁对新路径的搜索能力，各租赁点间路径上的信息素均被初始化为Tij（O）=c，c为常数，通常取0。

3）选择策略。蚂蚁在运动过程中，根据各条路径上的残留信息素浓度Tij和路径上的启发式信息ηij来计算选择下一个租赁点的概率。蚂蚁k在t时刻由租赁点ui运动到租赁点uj的概率用pij（t）来表示。式中：allowedk={U-tabuk}表示蚂蚁k尚未走访的租赁点集合；a为信息启发式因子，代表调度路径的相对重要性，反映了蚂蚁在运动过程中所积累的信息素浓度在蚂蚁选择运动路径时所起的作用；β为期望启发式因子，代表能见度的相对重要性，反映了蚂蚁在运动过程中启发信息在蚂蚁选择路径中的受重视程度。启发函数ηij表示调度车自租赁点ui至租赁点ui的期望程度，ηij=l/tij。

4）信息素更新。为了避免残留信息素过多所引起的残留信息覆盖启发信息，在每只蚂蚁完成对所有n个租赁点的遍历（亦即一个循环）之后，就要对全局残留信息进行更新处理。由此，在t+n时刻租赁点路径ιij上的信息素浓度可按如下规则进行更新调整：式中：p为信息素的挥发系数，1-p则表示信息素残留因子，p越小，算法的收敛性越高，但会降低蚂蚁的全局搜索能力，取值范围通常为0

3.2 蚁群算法改进

在真实的蚂蚁寻优过程中，存在信息素浓度越高，信息素挥发越快这一现象。虽然这样有效防止了一些路径上的信息素浓度无限制的增长，但当一些路径上的信息素浓度减少到零之后，算法就有可能陷于局部最优的困境。为此，本文对基本蚁群算法中信息素的更新策略对如下改进，当蚂蚁完成一次循环之后，路径上的信息素根据以上2个式子进行全局更新。

基本蚁群算法信息素更新中，即使部分信息素的浓度相差甚大，但其挥发的速率也是相同的。按照上述2个式子进行算法的全局更新，将挥发系数由常量p转变为以Tij（t）为变量的正比例函数，可依据信息素浓度与挥发速率的同向关系调整信息素，避免一些路径上的信息素浓度过早减少到零，从而导致算法过早收敛于局部最优。式（11）中Q为信息素强度，本文在不同阶段的蚂蚁寻优循环中，Q采取了不同的值，在算法初始阶段采取相对较小的值，使得路径上的信息素浓度变化较慢，尽量避免算法过早收敛到局部最优，而在算法寻优后期采取相对较大的值，从而增强算法的正反馈效应，搜索出最优路径。

4 实例研究

4.1 数据源

本研究选取宁波市海曙区段塘片区16个公共自行车租赁点作为实验样本，对调度中心采集提取的实时公共自行车在桩数据进行统计预处理发现，在一天的08：00-09：00时段，上述16个公共自行车租赁点的车辆流动性最大，通过聚类的分析方法确定了各个租赁点的最佳调度时间窗和可接受调度时间窗，分别代表公共自行车系统的预调度时段和车辆数报警至租赁点发生空满桩现象的过渡缓冲时段；在各个租赁点装卸公共自行车的服务时间与调入出量成正比，为10辆车每分钟；调度车辆的最大载荷为25辆公共自行车；由Google maps获取海曙区调度中心宁波公交新典路站的经纬度为（121.520791，29.863554），为便于区分，去掉东经及北纬相同的部分，改为（20791，63554），下同，如表1所示。

4.2 路径优化

运用本文提供的改进蚁群算法对上述模型进行求解。以Matlab为工具，初始参数设置为：a=l：β=i；p=o.1；NCmax=500。通过使用本文提出的方法，运算结果最终得到最优调度路径，如图2所示，仿真结果显示完成本次调度工作需要3辆车，各辆车的调度子路径如下，O代表调度中心。

子路径1：0-128-165-159-0

子路径2：0-153-157-155-0

子路径3：0-119-17-19-27-30-150-162-163-164-177-O

4.3 结果分析

对宁波市海曙区段塘片区的公共自行车租赁点的运营现状跟调度现状进行分析，利用Matlab编程实现蚁群算法求解带时间窗的城市公共自行车调度模型，其中：运用基本蚁群算法求解该模型的满意度为3.4286，改进蚁群算法得到的满意度为4.3529，相比于基本蚁群算法满意度提升了26.96%。

通过实例仿真结果比较，本文所改进的蚁群算法是可行的，在车辆调度路径方面，相比于基本蚁群算法，解的质量有所提高，收敛速度有所提升。同时也可以看出，本文所改进的蚁群算法对于解决城市公共自行车车辆路径问题是有效的，能够快速地收敛到全局最优解。