基于ECM模型和库兹涅茨曲线的区域能源消费峰值研究——以重庆市为例

王　胜，吕指臣，刘　贞，朱开伟，蒲刚清

(1.重庆社会科学院，重庆　400020； 2.重庆理工大学 管理学院， 重庆　40054；

3.美国劳伦斯国家能源实验室，美国 加州　94530)



基于ECM模型和库兹涅茨曲线的区域能源消费峰值研究
——以重庆市为例

王胜1,2，吕指臣1，2，刘贞2，3，朱开伟2，蒲刚清2

(1.重庆社会科学院，重庆400020； 2.重庆理工大学 管理学院， 重庆40054；

3.美国劳伦斯国家能源实验室，美国 加州94530)

摘要：以重庆市为例，选取1997—2013年的GDP、人均GDP、城镇化率和工业比重等统计数据，研究影响能源消费和经济发展相关因素的关系，结合协整检验、Granger因果检验、误差修正模型(ECM)和库兹涅茨曲线，运用定量分析方法进行分析，预测能源消费峰值，揭示能源消费与经济发展动态关系。结果表明：能源消费与人均GDP、城镇化率、工业比重分别有着单向、双向、单向的因果关系。根据长期均衡方程和ECM预测出2020、2025、2030年重庆市的能源消费情况，结合GDP和能源消费的库兹涅茨曲线,重庆市能源消费将在2028年达到峰值。研究结果与我国总体能源消费目标吻合，能够为我国城市能源消费规划及政策制定提供参考依据。

关键词：能源消费峰值；人均GDP；城镇化率；库兹涅茨曲线

一、引言

2014 年11月12日，国家主席习近平和美国总统奥巴马在北京发布联合声明：中国计划到2030年达到二氧化碳排放峰值，并争取提早实现这一目标；根据《华尔街日报》援引美国官员的消息称，中国将同意化石燃料在整体能源使用中的比重降至80%左右；在2013年6月、9月及2014年3月，习近平与奥巴马的3次会晤，都把双方在气候变化、能源与环境方面的合作作为重要内容[1]。我国是能源消费大国，能源消费的预测是能源规划制定的重要依据，目前中国的大部分一线城市正处于城市化、工业化的快速发展阶段，伴随着经济水平的大幅度提高，能源消耗的强度也越来越大。合理地分析和预测能源消费的情况有助于各个城市全方位的和谐发展。研究能源消费和经济发展、工业化程度等因素的关系怎么样，能否根据它们的关系来预测未来能源需求，我国能源消费能否在2030年前达到峰值，具有重要的现实借鉴意义。

国内外不少学者针对能源消费和经济发展间关系进行了相关研究。K Fatai等通过研究能源消耗和实际GDP增长的关系，在比较节能政策对新西兰、澳大利亚及一些亚洲经济体的影响后得出，相对于亚洲经济体，节能政策在新西兰和澳大利亚对GDP的增长可能没有显著的影响[2]。Hu Jin-Li等通过分析非线性框架下台湾的GDP和被分解的能源消费之间的关系，采用协整检验及向量误差修正模型验证GDP增长和能源消费的调整阈值[3]。Sabrinayan等通过收集美国2000—2011年的动态面板数据GMM-system估计量进行分析，说明能源消费和GDP之间具有单向因果关系,并通过建立GDP模型和能耗模型说明能源消费对GDP的影响程度[4]。Paraskevi K等应用7个国家最近的两个时间序列，重新检验能源消费和实际GDP及资本存量的因果关系，认为实际GDP对能源消费的影响起到主导作用[5]。Angeliki在分析过去20年研究GDP增长和能源消费关系的文献后认为，研究能源消费和GDP的长期弹性，不仅仅是通过对GDP和能源消费建立协整方程进行分析，还有一些诸如价格水平和资本这样的因素应该进入到协整方程中[6]。韩智勇等通过研究1978—2000年中国能源消费与经济增长的协整性和因果关系，得出中国能源消费与经济增长之间存在双向的因果关系，但不具有长期的协整性[7]。肖涛等使用面板数据计量分析方法，根据中国的8个经济区域22年的相关数据分析了各区域能源消耗与经济增长之间的关系，结果表明不同地区的能源消耗与经济增长存在不同的Granger因果关系[8]。陈操操等采用协整分析并建立VECE模型检验北京市1980—2008年能源消费与经济增长的因果关系，表明北京市经济发展对能源消费的提升是滞后的，能源消费并不是经济增长的强外省变量[9]。汪旭晖等使用协整分析方法和Granger因果检验，以中国1978—2005年能源消费和GDP数据为基础进行了实证研究[10]。樊元等通过JJ协整检验和向量误差修正模型，基于甘肃省1985—2010年的数据运用定性和定量结合的方法对其短期及长期影响关系进行了实证分析[11]。薛黎明等应用协整原理，对中国煤炭消费与经济发展水平之间的关系进行了协整分析与因果关系检验，得出煤炭工业健康发展的实施基础[12]。何剑等利用2002—2008年数据，运用面板数据模型、协调度计算等方法对中国西北五省区能源消费与经济发展的协调状况进行研究[13]。

关于能源消费及其峰值预测进行的研究有：董锋等运用灰色关联分析方法研究GDP、技术进步和对外开放程度等因素对能源消费的影响，提出国家需要对相关政策进行调整以应对能源的需求[14]；宁亚东等采用完全因素分解模型，对中国一些部门能源消费特征进行量化分析来研究影响能源消费的因素[15]；岳婷等通过建立人均生活用能量与其影响因素之间的VAR模型验证它们与不同能源消费品之间的消耗关系[16]；杨波等建立算法优化后中国国家能源消费总量Logistic模型，根据历史数据预测未来20年的国家能源消费情况[17]；渠慎宁等利用STIRPAT模型对中国碳排放峰值进行了预测，得出碳排放峰值在不同的技术情景下出现的时间段[18]；朱永彬等在对内生经济增长模型进行改进的基础上预测了中国能源消费与碳排放高峰[19]；何建坤通过分析国内外能源消费和CO2排放达到峰值的耗时，结合数学模型分析预测我国能源消费和CO2排放将在2030年左右达到峰值的不确定性，提出相关政策建议及战略对策[20]。

综合以上文献，国内外研究皆有从国家层面分析GDP增长和能源消费关系，从面板数据到时间序列，通过不同区域和国家比较，来解释它们之间存在的因果关系，以期得出相关结论来影响宏观政策调整。有学者通过建立模型(如运用灰色、BP、协整等方法)研究能源消费和GDP的关系，说明能源消费和经济发展关系的问题正在被广泛关注。

目前针对能源消费情况，依据国家或者某一区域的经济发展、城市化规模以及工业化的比重对能源消费进行研究尚不多见。从实际意义上来看，根据模型本身的优势，建立的误差修正模型能更好地预测短期的能源消费情况。在此基础上，针对国家或城市的发展状况，结合能源消费的情况，提出相应的政策建议，能够更有效地跟随和响应国家的政策。本文以极具代表性(正快速发展)的城市——重庆为例，通过重庆市的经济发展(人均GDP)、城市化规模(城镇化率)及工业化程度(工业产值比重)等因素对能源消费情况进行预测分析；主要使用计量经济学方法和Eviews软件工具[21]，研究能源消费和人均GDP、城镇化率、工业比重之间的关系，检验其协整性，并得出其长期的均衡方程，然后判断它们之间的Granger因果关系，建立误差修正模型，预测出2015—2030年重庆市的能源消费情况。借助协整理论，检验能源消费和实际GDP变化的库兹涅茨曲线的存在性，确定能源消费量达到拐点时的量，并确定重庆市能源消费量达到峰值的时间，以期为我国城市能源政策的制定及发展规划提供新的思路。

二、能源消费预测中的计量模型与分析

(一)变量的选择

参照相关研究发现，影响能源消费的潜在因素有很多，本文通过对可能的影响因素如第三产业比重、常住人口增长率、汽车拥有量增加值、人口自然生长率、GDP、人均GDP、工业比重、城镇化率、能源消费结构变化、建筑业比重等因素进行检验，确定下来直接影响能源消费的因素为GDP、人均GDP、城镇化率和工业比重。

1.GDP和人均GDP

GDP和人均GDP很好地反映了一个区域的经济发展程度，通常情况下，GDP和人均GDP的变动也映射出能源消费的变动，伴随着人均GDP的增加，将会导致能耗的不断增长。

2.城镇化率

由于农村居民和城镇居民的消费水平和方式有很大区别，城市规模的不断扩大，意味着城镇化程度越来越高，也意味着能源消耗的大幅度提高。使用大量建材、钢铁、电力等能源建设基础设施和住房等，势必会导致能源需求增长，因而城镇化率可以很好地估计能源消费的情况。

3.工业比重

一般情况下，一个区域的能耗水平很大程度上体现在工业的发展状况上，工业比重也直接反映了高能耗行业的占比，目前重庆市正处于工业化发展关键阶段，预测能源消费，工业产值具有很好的衡量效果。

鉴于重庆市成为直辖市后的经济形势不同，重庆的内外环境发生了巨大的变化，本文选取1997—2013年重庆能源消费总量、城镇化率以及工业比重来研究能源消费与经济发展之间的关系。能源消费总量及其构成的数据来源于《重庆统计年鉴(2014)》[22]，单位为万吨标准煤；GDP数据来源于《重庆统计年鉴(2014)》[22]，并以1997年为基期，折算为不变价格的实际GDP，单位为亿元，人均GDP也同样处理。为消除异方差性及便于经济意义分析，对所有数据取自然对数处理。

(二)数据的处理

1.各变量的含义说明

GDP、TE、GDPPC、UR、IR分别表示国内生产总值、能源消费总量、人均GDP、城镇化率、工业比率(工业产值占总产值的比重)，其自然对数表示为LGDP、LTE、LGDPPC、LUR、LIR，自然对数的一阶差分表示为DLGDP、DLTE、DLGDPPC、DLUR、DLIR。DDLGDP、DDLTE、DDLGDPPC、DDLUR和DDLIR分别表示LGDP、LTE、LGDPPC、LUR、LIR的二阶差分。根据1997—2013年的数据，通过Eviews 6.0画出以上因素的时序图,如图1和图2。

图1　各种变量对数的时序

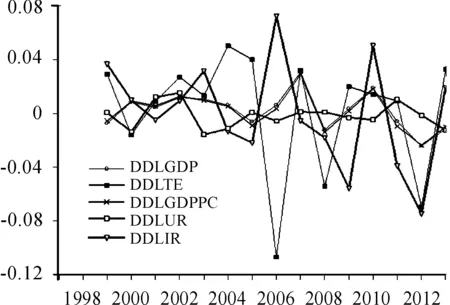
图2　对数二阶差分时序

2.各变量时间序列的平稳性检验

在进行协整分析之前，需要对数据的平稳性进行检验，采用的方法是单位根检验。单位根检验有DF 检验、ADF 检验和PP 检验3种,本文采用的是目前使用最为广泛的ADF 检验。其检验过程基于如下的OLS 回归：

(1)

式中，t表示时间趋势项，选择滞后阶数p，使εt为白噪声序列。检验YT中出现单位根的零假设相当于检验式(1)ρ=0 的原假设。如果ρ显著小于零，则拒绝存在单位根的零假设。滞后阶数根据AIC 准则选取，各单位根的临界值则均由Eviews6.0软件给出。各时间序列的平稳性检验数据如表1 所示。

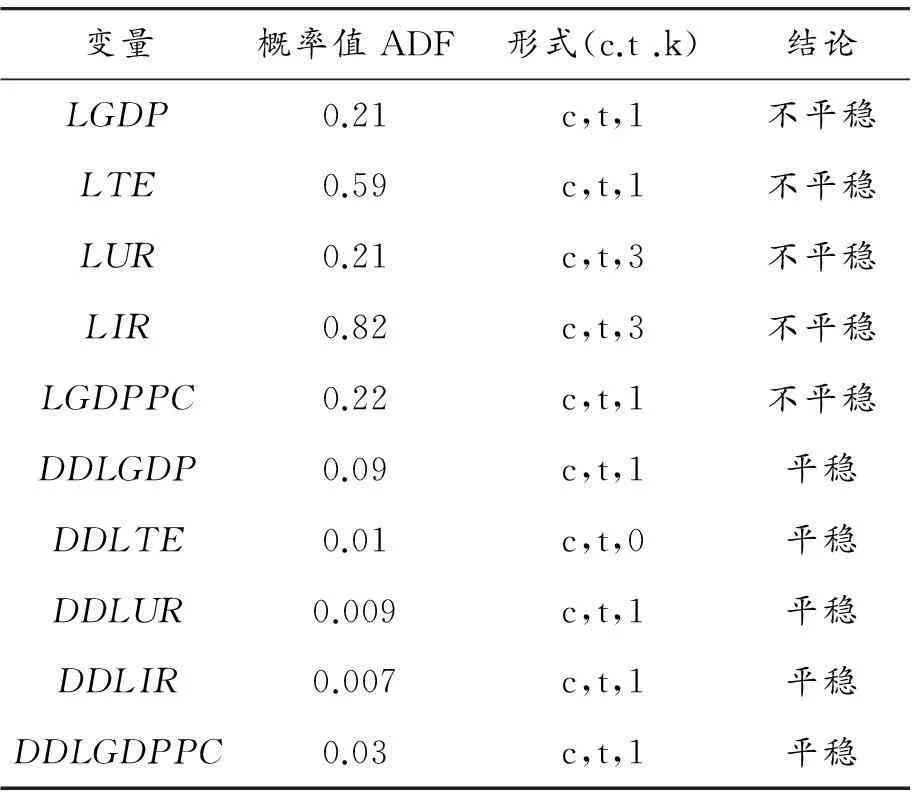
表1　各种变量的单位根检验结果

注：结果由Eviews6.0得出，c和t表示带有常数项和趋势项，k表示滞后阶数[23]。

表1中ADF值概率小于0.1通过平稳性检验。由检验结果可知，各变量的一阶差分均不平稳。且LTE与LGDP、LGDPPC、LUR、LIR均为二阶单整序列，所以它们之间有可能存在协整关系，也有必要对其进行协整检验。

三、协整检验

关于协整理论的检验和估计有许多方法，如EG两步法、Johansen极大似然法、自回归分布滞后模型(ARDL)法等，鉴于本文上述平稳性检验结果表明各变量都是二阶单整序列，此处采用EG两步法。

首先对能源消费和GDP、人均GDP、城镇化率、工业比重的对数分别建立适当模型，通过检验模型残差是否属于平稳序列判别它们是否协整。再对能源消费和GDP、城镇化率、工业比重的对数建立模型，检验其残差。最后对能源消费和人均GDP、城镇化率、工业比重的对数建立模型，检验残差，若残差通过检验，则表明它们协整。

(一)模型建立

LTE=1.43 + 0.85LGDP

LTE=0.24 + 0.86*LGDPPC

LTE=-1.30 + 2.55*LUR

LTE=-7.34 + 4.28*LIR

LTE=-1.62 + 0.36*LGDP+

1.19*LUR+ 0.7*LIR

LTE=-1.91 + 0.42*LGDPPC+

1.03*LUR+ 0.65*LIR

通过对上面模型残差进行检验，残差u1、u2、u3均通过检验，原假设中拒绝零假设H0，意味着残差项u1、u2、u3都是平稳序列；u4通不过检验，说明LTE分别与LGDP、LGDPPC、LUR是协整的，LTE和LIR不是协整的。但当使LGDP、LGDPPC分别和LUR、LIR结合建立模型时，u5、u6通过检验说明，组合因素共同影响能源消费时它们是协整的，具体显示如表2。

(二)长期均衡方程

LTE=1.43+ 0.85*LGDP + 1*u1

LTE=0.24+0.86*LGDPPC+1*u2

LTE=-1.30+ 2.55*LUR + 1*u3

LTE=-7.40+ 4.28*LIR + 1*u4

LTE=-1.62 + 0.36*LGDP +

1.19*LUR + 0.7*LIR + 1*u5

LTE=-1.91 + 0.42*LGDPPC+

1.03*LUR + 0.65*LIR + 1*u6

根据Granger定理，如果若干个变量之间存在协整关系，则这些变量必然有误差修正模型(ECM)表达式存在，反之也成立。对变量进行单整性检验来检验序列平稳性后，检验变量之间是否存在协整性关系，如果存在协整关系则可以建立误差修正模型。误差修正模型可以将长期关系与短期动态特征结合在一个模型中，利用该模型来分析能源消费影响因素是合理的。

表2　残差检验结果

四、误差修正模型

根据Granger定理，一组具有协整关系的变量具有误差修正模型的表达形式，其作用在于不依赖某些解释变量。而仅仅依靠解释变量和因变量之间的长期关系的偏差以及因变量的调整，便可以解释经济中不同变量之间的长期稳定关系和自身变化的过程。误差修正模型(Error Correction Model，简记为ECM)是一种具有特定形式的计量经济学模型，它的主要形式是由Davidson、 Hendry、Srba和Yeo于1978年提出的，也常被称为DHSY模型[27]。假设具有如下(1，1)阶分布滞后形式：

(2)

模型显示出第t期的Y值，与X的变化和t-1期的X与Y的状态值有关，对(2)变形得：

(3)

式中，λ=1-μ，α0=β0/(1-μ)，α1=(β1+β2)/(1-μ)

式(2)称为一阶误差修正模型，模型(3)可以写成：

(4)

(一)GDP、能源消费、城镇化率、工业比重的误差修正模型

DLTE=0.53*DLGDP+0.72*DLUR+

0.43*DLIR-0.56*u5(-2)+

0.01*DLTE(-1)

(u5= LTE+1.62 -0.36*LGDP-

1.19*LUR-0.7*LIR)

该模型表明：GDP、城镇化率、工业比重的变化将引起能源消费相同方向的变化，即短期内GDP变化1%将导致能源消费同方向变化0.53%，城镇化率变化1%则引起能源消费同方向变化0.72%，工业比重变化1%则引起能源消费同方向变化0.43%，且DLTE(-1)显示了能源消费上期对本期变化有着显著的促进作用。而残差项即误差修正项u5则体现反向修正作用，表明了长期非均衡误差对LTE的控制。

(二)人均GDP、城镇化率、工业比重和能源消费误差修正模型

DLTE=0.69*DLGDPPC+0.61*DLIR-

0.69*u6(-2) - 0.67*DLTE(-1)

(u6=LTE+1.91-0.42*LRJGDP-

1.03*LCZ-0.65*LGY)

该模型表明：人均GDP、城镇化率、工业比的变化将引起能源消费相同方向的变化，即短期内GDPPC变化1%将导致能源消费同方向变化0.69%，工业比重变化1%则引起能源消费同方向变化0.61%，DLTE(-1)则显示了上期对本期有抑制作用。而残差项即误差修正项u6则体现反向修正作用，表明了长期非均衡误差对LTE的控制。

1.Granger检验

Granger因果关系检验的基本模型为：

模型中，s，k分别代表被解释变量和解释变量滞后阶数。利用最小二乘法进行参数估计，用F统计量来进行Granger因果关系分析。检验的原假设H0∶βj=0(j=1,2,…,k)，如果F统计量计算值大于F临界值，则拒绝原假设，及x是y的Granger原因。根据模型及数据检验结果见表3所示。

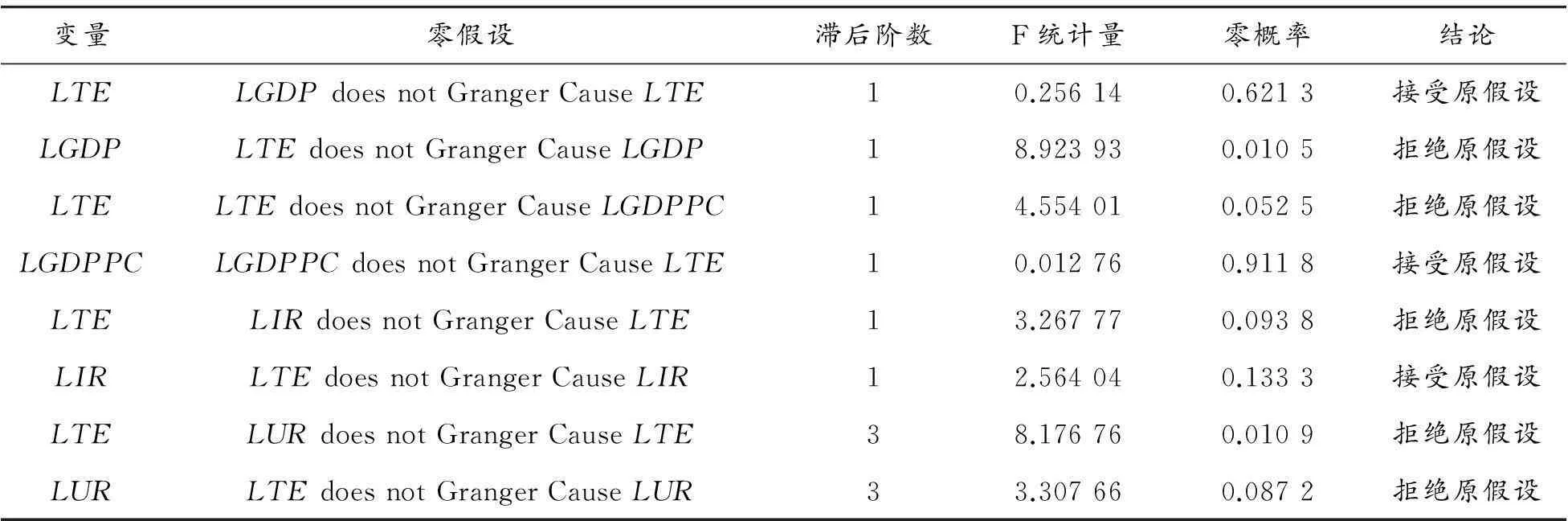
表3　1997—2013年Granger因果关系检验

城镇化率和能源消费之间的Granger检验结果表明：能源消费和城镇化率是双向的因果关系，拒绝原假设，能源消费对数不是城镇化率的原因，城镇化率不是能源消费的原因。同理说明：工业对数是能源消费的Granger原因，即是单向的因果关系。人均GDP和能源消费是单向的因果关系，即能源消费是人均GDP的单向因果关系。

五、能源消费预测

通过对重庆市1997—2013年人均GDP、GDP、城镇化率、工业比重和能源消费进行协整关系分析，建立模型，并通过Granger因果关系检验，根据其长期均衡方程和误差修正模型得出预测值。由于人均GDP相对于总量GDP在和城镇化率、工业比重结合建立模型时拟合度更高，更具有说明意义，此处选择模型中的能源消费和人均GDP、城镇化率、工业比重进行预测。

图3标示的是模型在样本区间内的实际值和预测值的误差，由计算结果可知，它们的误差在2%～9%的较小范围内。

为实现对重庆市能源消费的预测和评价，我们需要对模型中的因素设定参数，预计到2020年全市常住人口为3 400万人，城镇化水平为70%,再参照国家整体规划，根据2009—2013年城镇化率的平均增幅推算2016—2020年及2025、2030年城镇化率。

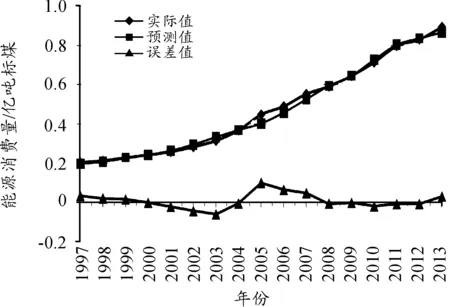
图3　能源消费的预测值、实际值和误差

同样，根据2009—2013年常住人口的平均增幅，以及2014年重庆市规划局的调整计划，可推算2016—2030年重庆市的常住人口，而根据重庆市GDP的增幅近阶段处于9%的平均增幅，推算出重庆市2016—2030年人均GDP(人均GDP=GDP/常住人口)。

目前，重庆工业占比为42%左右，且有下降趋势，但依据“十二五”规划及现阶段重庆市发展状况，重庆市仍处于工业的大力发展阶段，根据2009—2013年的工业比值平均增幅，推算2016—2030年的工业比重。参数设置如表4。

表4　参数设定值

注：人均GDP和工业比重已按1997年不变价格折算过。

资料来源：《重庆城乡总体规划(2007—2020)》《城乡规划调整-重庆市规划局(2014年)》《重庆市人民政府关于推进新型城镇化的若干意见(2012年)》。

基于上述分析，得出能源需求预测值如表5。

六、重庆市GDP和能源消费趋势

库兹涅茨模型构建的理论依据是20世纪90年代初美国经济学家Grossman 和Krueger提出的描述环境污染和经济发展之间演替关系的环境库兹涅茨曲线(EKC)理论[24]。运用库茨涅兹曲线得出能源消费和经济增长的一般模型如下:

(6)

在实际模型构建中,影响能源消费和经济增长的其他因素Z项在计算和模拟过程中常忽略不计,国内外学者通常选用的简化模型有:

(7)

简单的库兹涅茨曲线描述了GDP和能源消费的关系[25]，本文选择GDP作为解释变量并使用对数的二次方程形式，其库兹涅茨模型表达式：

(8)

式(8)中，LGDP表示对GDP取对数；(LGDP)2表示对GDP取对数的平方；α表示反应个体差异的变量；ωit表示随机误差项。

表52015—2020能源消费量

万吨标准煤

由图1可知能源消费和GDP均有随着时间上升的趋势，此处首先对(LGDP)2序列进行平稳检验，根据Eviews6.0检验(LGDP)2同样是二阶差分平稳序列，对LTE、LGDP、(LGDP)2做协整检验得到静态回归方程为：

LTE=-10.12+3.79LGDP-0.18(LGDP)2

由回归方程可以看出，其显著性、回归系数及相关系数的显著性比较好，进一步检验LTE、LGDP和(LGDP)2是否有长期协整的关系。对其残差序列u7进行检验，结果如表6。

表6　残差检验

从检验结果得出，残差序列的统计量t值为-2.335 899 1，其在5%和10%的显著水平下均拒绝了存在单位根的假设，说明残差序列稳定。得出LTE、LGDP和(LGDP)2有显著的协整关系，即长期均衡，如表7。

表7　方程常数项系数及拐点值

根据表7及静态回归方程得出，重庆市能源消费存在库兹涅茨曲线，并可以得出能源消费峰值为18 582.95万吨标准煤。结合上述能源预测，此拐点值与上述预测的2028年能源消费量18 742.53 万吨标准煤接近，可以得出重庆市能源消费将会在2028年达到峰值。

七、结论

重庆市能源消费将会在2028年达到峰值，但2030年的预测值明显又大于峰值点，这说明目前重庆市对能源利用的能效无法满足重庆市城镇化和工业发展的需求，需要对第二产业结构进行优化，大力发展环保产业和低能耗产业，提高工业生产技术水平，减少高能耗行业比例，降低能耗，使能源得到合理可持续的利用。

城镇化率和能源消费存在着双向的Granger的因果关系，这说明城镇化率对能源消费有依赖作用，能源促进了城镇化率的提升，而且城镇化程度也能充分反映能源消耗变化程度。能源消费和人均GDP有着单向的Granger因果关系，说明能源消费的增长可能暗含着人均GDP 的增长。GDP和能源消费有着单向的Granger因果关系，且GDP增长明显促进了能源消费的增加，说明能源消费要以经济的增长为前提。通过预测的能源消费总量值显示，近期重庆市的能源需求还是在稳步增长，意味着经济的发展也在同步进行。工业比重和能源消费有着单向的Granger因果关系，即工业比重的变化将会导致能源消费同方向的变化，需要调整工业比例，根据能源的供应状况合理调整工业发展。

本研究采用的是多因素变量构建计量模型研究能源消费情况，结合目前间接预测能源的一些其他模型可以看出，可能需要考虑更全面的因素，甚至组合相关的模型来预测或者衡量能源的需求，以保障重庆市的能源发展和国家对重庆市能源的支持政策同步。

参考文献：

[1]东方早报.中美达成减排协议：中国计划 2030年左右碳排放达到峰值[EB/OL].http://www.dfdaily.com/html/21/2014/11/13/1203646.shtml.2014.

[2]FATAI K,OXLEY L,SCRIMGEOUR F G.Modelling the causal relationship between energy consumption and GDP in New Zealand,Australia,Indiia,Indonesia,The Philippines and Thailand[J].Mathematics and computers in simulation,2004,64(3/4):431-445.

[3]JIN-LI Hu,CHENG-HSUN Lin.Disaggregated energy consumption and GDP in Taiwan:a threshold cointegration analysis[J].Energy economics,2008,30(5):2342-2358.

[4]SABRINAYAN,NORSIAHKADIR,MAHYUNDIN A,et al.Revisiting energy consumption and GDP:evidence from dynamic panel data analysis [J].Procedia economics and finance,2013(7):42-47.

[5]PARASKEVI K，SALAMALIKI,Ioannis A.Energy consumption and real GDP in G-7:multi-horizon causality testing in the presence of capital stock [J].Energy economics,2013，39:108-121.

[6]ANGELIKI N.MENEGAKI.On energy consumption and GDP studies; a meta-analysisof the last two decades [J].Renewable & sustainable energy reviews,2014，29:31-36.

[7]韩智勇，魏一鸣，焦建玲，等.中国能源消费与经济增长的协整性与因果关系分析[J].系统工程，2004,22(12):17-21.

[8]肖涛，张宗益，呙小明.八大经济区能源消耗与经济增长关系的实证研究[J].科研管理，2012,33(4)：139-146.

[9]陈操操，张妍，刘春兰，等.北京市能源消费与经济增长关系的协整检验分析[J].环境科学，2012，33(6):2139-2144.

[10]汪旭晖，刘勇.中国能源消费与经济增长：基于协整分析和Granger因果检验[J].资源科学，2007,29(5)：57-62.

[11]樊元，刘亚丽，陈晶.甘肃能源消费与经济增长动态影响关系实证分析——基于JJ协整检验和误差修正模型[J].数学的实践与认识，2013,43(18)：39-45.

[12]薛黎明，侯运炳，蔡先锋，等.中国煤炭消费与经济发展水平之间关系的协整分析[J].中国矿业，2011,20(1)：31-35.

[13]何剑，季俊.中国西北五省区能源消费与经济发展的协调性分析[J].资源与产业，2012,14(4)：19-24.

[14]董锋，谭清美，周德群，等.技术进步、产业结构和对外开放程度对中国能源消费量的影响——基于灰色关联分析-协整检验两步法的实证[J].中国人口·资源与环境，2010,20(6)：22-27.

[15]宁亚东，丁涛，外冈丰.中国能源消费特征分析——基于完全因素分解模型的实证研究[J].大连理工大学学报，2012，52(5)：641-647.

[16]岳婷，龙如银.我国居民生活能源消费量的影响因素分析[J].华东经济管理，2013,27(11)：57-61.

[17]杨波，谭章禄.基于Logistic模型的中国国家能源消费总量预测研究[J].科技管理研究，2013(12)：45-48.

[18]渠慎宁，郭朝先.基于STIRPAT模型的中国碳排放峰值预测研究[J].中国人口·资源与环境,2010,20(12):10-15.

[19]朱永彬，王铮，庞丽，等.基于经济模拟的中国能源消费与碳排放高峰预测[J].地理学报，2009，64(8)：935-944.

[20]何建坤.CO2排放峰值分析:中国的减排目标与对策[J].中国人口·资源与环境，2013,23(12):1-9.

[21]张晓峒.EViews使用指南与案例[M].北京：机械工业出版社，2007.

[22]重庆市统计局.重庆统计年鉴(2014)[Z].北京：中国统计出版社，2014.

[23]李子奈.高等计量经济学[M].北京:清华大学出版社，2002.

[24]GROSSMAN G，KRUEGER A.Economic growth and the environment[J].Quarterly journal of economics,1995,110(2):353-377.

[25]夏自兰，赵小凤，王继军.江苏省环境库兹涅茨曲线特征及其成因分析[J].水土保持研究，2010,17(1)：198-206.

(责任编辑魏艳君)

Research on Regional Energy Consumption Peak Based on ECM Model

and Kuznets Curve: Take Chongqing as an Example

WANG Sheng1,2, LYU Zhi-chen1,2, LIU Zhen2,3, ZHU Kai-wei2, PU Gang-qing2

(1.Chongqing Academy of Social Sciences, Chongqing 400020, China；

2.College of Management, Chongqing University of Technology, Chongqing 400054, China;

3.Lawrence Berkeley National Laboratory, California 94530, US)

Abstract:Taking Chongqing as an example, we selected GDP, per capita GDP, urbanization rate and the proportion of industrial statistics from 1997 to 2013, and studied the factors affecting energy consumption and economic development, and combined with the co-integration test, Granger causality test, error correction model (ECM) and Kuznets Curve, and used quantitative analysis method, we analyzed and discussed the relationship between them by predicting the peak of energy consumption, to reveal the dynamic relationship between energy consumption and economic development. The results show that the energy consumption and per capita GDP, urbanization rate, industrial proportion respectively has a one-way, two-way and one-way causal relationship respectively. According to the long-term equilibrium equation and the ECM, we predicted energy consumption situation of Chongqing of 2020, 2025, 2030 respectively, and combined with the GDP and energy consumption of the Kuznets curve, energy consumption in Chongqing will arise its peak in 2028. The results accord with China’s overall energy consumption targets, conduce to comprehensive deal with the problem of energy demand, the urban energy consumption planning and policy in making provide reference .

Key words:energy consumption peak value; per capita GDP; rate of urbanization; Kuznets curve

文章编号：1674-8425(2016)01-0037-09

中图分类号：F206

文献标识码：A

doi:10.3969/j.issn.1674-8425(s).2016.01.007

作者简介：王胜(1976—)，男，四川乐山人，研究员，博士，重庆社会科学院副院长，重庆市人民政府发展研究中心副主任兼秘书长，研究方向：低碳经济、能源政策规划与设计、区域能源消费；吕指臣(1989—)，男，河南泌阳人，硕士研究生，研究方向：技术经济及管理。

基金项目：国家自然科学基金“能源安全和生态环境约束下区域农业生物质能经济总量模型与补偿机制研究”(71573026)；重庆市教委人文社会科学研究项目“总量控制下的区域能源安全预测预警体系研究”(13SKL10)；重庆市重大决策咨询研究课题“重庆市能源安全风险评估及其对策研究”(2DKB12007)；重庆市人文社会科学重点研究基地开放基金项目“不同政策情境下的低碳消费行为实验研究”(2015Q53)

收稿日期：2015-06-19

引用格式：王胜，吕指臣，刘贞，等.基于ECM模型和库兹涅茨曲线的区域能源消费峰值研究——以重庆市为例[J].重庆理工大学学报(社会科学)，2016(1):37-45.

Citation format：WANG Sheng, LYU Zhi-chen, LIU Zhen,et al.Research on Regional Energy Consumption Peak Based on ECM Model and Kuznets Curve: Take Chongqing as an Example[J].Journal of Chongqing University of Technology(Social Science)，2016(1):37-45.