中国碳交易市场CO2排放权地区间分配效率研究
傅京燕 黄芬
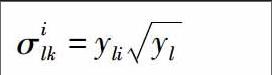


摘要:由于我国地区间资源禀赋和经济发展水平存在差异,在碳排放总量一定的前提下,充分考虑地域间的差异以选取合理的地区间分配方式对实现2016年全国统一碳市场的建立至关重要。本文试图通过零和DEA模型寻求一种新的碳排放权分配方式,在考虑地区间人口和经济差异的基础上实现满足DEA的效率性水平。本文首先通过零和DEA模型对历史排放分配法的效率性水平进行评估,由于历史排放分配法主要受能源消费模式和产业结构决定,不能全面的反映不同地区间的发展和资源禀赋等情况,导致减排成本分配的不合理,从而缺乏效率性;然后根据初次零和DEA的评估结果,通过多次迭代法进行投影,计算出效率性最大化的地区分配方案,从最终的分配结果来看,江苏、山东和广东三省的综合产出因素值高于其他省市地区,最终的CO2排放权分配数量也最多,说明在零和DEA方法下,各地区排放权的分配数量与该地区的经济总量和人口数量成正比;最后,在影响CO2排放的因素中,能源强度和经济发展水平影响最为明显。这说明从短期看,受经济发展要求和要素禀赋的限制,我国碳排放量的绝对值在未来一定时期内仍将处于上升阶段。
关键词:分配效率;碳排放配额;碳交易市场
中图分类号 F328 文献标识码 A 文章编号 1002-2104(2016)02-0001-09 doi:10-3969/j-issn-1002-2104-2016-02-001
碳交易体系的基本环节主要包括总量限制制度、排放权分配制度、交易制度、柔性机制以及监管和处罚机制等等。其中,排放权作为一种有价资产,所有者可以通过出售多余的排放权来提高自身福利水平,从而影响社会福利的再分配。即使分配方法不会直接影响总体的减排目标,但具体的分配方法能否充分考虑各地区或产业的生产需要、成本增加的合理性,却是影响排放交易体系效率的关键。因此,排放权分配制度被认为是碳交易体系基本环节中最重要的环节。随着我国碳交易机制试点的顺利进行,加快建立全国碳排放交易市场也被提上了议事日程。全国碳交易市场的建立必须实现碳排放数据的精准,因为这将影响到企业参与的积极性和管制措施的有效性。这意味着全国各省市地区的排放总数不能超过一定数量的排放额。也就是说,各省市地区只能在确定的总碳排量内,通过一定的方式进行排放权的划分。此外,在全国碳交易市场实现运行之后,要充分考虑现有的七个试点省市,实现全国碳市场与这几个交易市场的兼容,这也是确保统一碳交易市场能够顺利建立和运行的必然要求。所谓“连接”,首先是指试点地区在核算方法上应按照国家统一标准进行调整;而全国碳市场与试点市场之间的连接同样需要合理设置排放权的分配方法。因此本文对一定数量排放权在各省市地区间的分摊标准进行研究,为全国统一碳交易市场的建立和有效运行提供参考。
1 文献综述
1.1 初始分配对碳交易市场运行效率的影响
排放交易体系包含两个步骤:首先是交易前的初始分配(一级市场),其次才是市场的构建或交易规则的制定(二级市场)。理论上来说,初始分配并不影响交易后的分配结果。根据科斯理论,在交易成本很小以至可以忽略不计的情况下,市场运行结果的效率性与产权初始分配无关。因此政府在设定初始分配方式时,就只考虑政策的可行性而不考虑市场的经济效率性。然而现实存在的不确定性,将导致市场运行产生实质性的交易成本,这使得经济学家开始研究初始分配对碳市场运行效率的影响。
Hahn[1]通过“单期单个企业单一价格”模型分析,指出存在市场势力情况下,初始分配不仅影响公平性,也关系到减排成本的有效性。减排成本的大小将受排放权初始分配的影响,因为产权的最终分配发证在不完全竞争的市场环境中;信息不对称和政策延迟等因素会使交易成本随之上升,导致许可权交易市场的均衡受排放权的初始分配影响(Stavins[2]);因而对排放权初始分配方法的设定和选择,与碳交易市场的运行息息相关。基于此,Sorrell and Skea[3]指出碳市场的建立包括多个不同环节,其中排放权的初始分配是关键步骤之一,也是最具争议的实施环节。事实上初始分配方式具有多样性,其带来的灵活性是一把双刃剑。一方面,它给决策者足够的维度去追求成本和收益的公平性和公正性;另一方面,可能使政策在使大多数团体获益的同时,而让少部分人承担超额的成本。
1.2 不同初始分配方式的公平性与效率性的比较
排放权的分配在理论上有两种方式:拍卖和免费分配,其中免费分配又主要有祖父制分配和基准制分配两种。初始分配不仅对市场结果有影响,而且影响很大。这不仅是因为不同的分配方式影响减排成本在不同个体间的的分配的公平性,也因为存在双重福利、企业的差别待遇、市场势力和市场受限等情况下,成本效率性的实现程度将取决于具体的初始分配方式(Burtraw[4]等)。
(1)从公平性角度, Sijm、Neuhoff 和Chen[5]根据对荷兰和德国电力批发市场的实证研究,发现电力生产者将配额的机会成本传导给下游消费者的比例从60%到100%不等,这意味着在免费分配方式下,电力消费者成为企业“意外之财”的买单者。此外,在消费者中,低收入人群的能源消费占收入比重高于高收入人群,成本增加占收入比重,低收入人群也高于高收入人群。Smale[6]的研究发现,除电力行业的其他行业,包括水泥和钢铁等高能源强度行业,尽管具有更大的贸易暴露度和价格需求弹性,仍具有通过调节产业和价格来从免费分配方式下获得“意外之财”的潜力。另外,从空间角度考虑,一定量排放权在不同地区间的分配方法要体现公平性,需要综合考虑各地区的经济发展水平,确保经济及排放大的地区承担更多的减排义务。而拍卖分配是最能体现市场机制作用的配额分配方式,将有限的排放指标通过公开竞标的方式进行拍卖,可以保证配额分配给了最需要的企业;因此出于公平性考虑,应该将无偿分配方式改为拍卖的分配方式。
(2)关于免费分配方法的效率性,Bohringer[7]提出,免费分配的基准原则下,企业缺乏有利于环境改善的创新和研究激励。这是因为创新和研究的发展使得环境改善,从而降低排放权的价值,也就是降低排放权所有者的福利水平,所以企业缺乏技术创新动力;其次,祖父制可能对新进企业形成准入壁垒,因为已有的企业免费获得排放权,而新进企业则必须向已有的企业购买(Howe[8])。另外,在历史分配法下,企业为尽可能多的获得排放权,可能会在排放交易体系建立之初增加污染排放。而拍卖的分配方式虽然短时间内增加了企业的成本,但从长期效益看,企业成本增加将迫使其积极创新,加大投入低排放技术的研发,在不断地技术积累下,企业将减少配额的需求量,同时也导致配额的市场价值下降,企业的利润进一步扩大;反之,那些堕于技术创新的企业将会被不断增加的成本拖累,最终影响企业地正常发展直至被市场淘汰。并且,政府通过拍卖的方式可以将获得的收入进一步投入到减排的工程中,大力扶持减排技术的创新,加快行业的发展水平。可见,拍卖较之免费的分配方式更具效率性。
1.3 DEA理论模型在环境效率方面的研究
DEA模型自提出以来,越来越多地被广泛用于各个领域的效率性研究。很多学者试图通过各种处理方式,将非期望产出纳入数据包络分析(DEA)模型分析框架中。EG Gomes[9]通过零和DEA模型将碳排放权作为投入变量,各国GDP、就业、出口额和能源使用量作为产出,得出了一定量排放权在欧盟各成员国间效率性的分配方法。Fare et al.[10]利用DEA模型就碳排放在欧盟28个国家在时间上的再分配进行了探讨。林坦和宁俊飞[11]通过零和DEA模型将各国GDP、人口作为产出,CO2排放量作为投入对欧盟各成员国的原始分配进行了再分配,得出了具有DEA效率性水平的排放权分配结果。
综上,目前对初始分配的研究,主要是从公平性和效率性的角度分析他们如何对碳市场和经济运行产生影响的及其程度,对不同的分配方式进行评价和优劣的比较,而少有对新的分配方式的探讨和分析。少数运用DEA模型进行初始分配方式效率进行评估的实证研究仅限于对欧盟或其他外国地区的排放权在时间和空间上的再分配,且仅考虑GDP、人口和能源消费的绝对值作为产出变量,忽略了产业结构和人口结构对CO2排放的影响。本文将碳排放权作为投入变量,通过零和DEA模型,计算具备DEA有效性的排放权分配结果。而这一分配方式不仅考虑了各地区的经济水平和人口总数,还综合了产业结构和人口结构因素,更加全面地考虑了地区的差异性,为我国实现不同地区碳市场的连接以及全国统一碳市场的建立的碳排放权在各个省市地区间的分配提供参考。
2 模型描述与数据处理
2.1 零和DEA模型
本文选取投入导向型的DEA模型进行估计。即将CO2排放权作为投入变量,评估在一定的经济水平和社会结构下各地区的CO2排放的效率水平,然后根据非效率水平值对CO2排放权进行再分配,也就是在代表经济水平和社会结构的产出变量数值一定的前提下,通过投入变量CO2排放的变动进行效率最大化的分配。
值得注意的是,传统的DEA模型假定各决策单元(DMU)之间相互独立,一个决策单位的投入产出的变动不影响其他单位,但是在评估排放权分摊时,我们将总排放权数量作为投入,而这一投入作为一个具体常数,并不随企业决策而增减。所以一个DMU的排放量增加(减少),必会使得其他DMU的排放量减少(增加)。在这种情况下,要计算排放权的效率性分摊结果需要对传统的DEA模型的限制条件修改为零和DEA模型进行估算。
零和即指总排放量不变,DMU决策单位之间,一方所得为一方所失。在投入导向模型中,若0为非DEA有效,假设其零和DEA效率值为θi,为了实现DEA有效,必须减少CO2排放权的投入,减少量为ΔXi=Xji(1-θi),并将这一数额按其他各DMU的CO2投入比例分配给其他DMU。由于各DMU都根据自身效率情况进行再分配,所以初次结果可能仍存在部分DMU非DEA有效的情况。本文采用迭代法对CO2进行数次再分配,最终得到所有DMU都达到DEA效率性的结果。
2.2 数据描述及变量处理
(1)CO2排放量。本文首先根据2005年各地区能源消费情况,选取包括煤炭、焦炭、原油在内的消费数量最多的九种能源的统计数据,分别对应IPCC于2006年公布的各种能源CO2的排放系数,得到各地区2005年的CO2历史排放数量,再根据2005年历年各地区GDP,得到2005年各地区碳排放强度,并且,为消除价格因素影响,本文所有涉及GDP数值的变量或指标均以2005年不变价格水平计算。其次,根据我国2020年碳排强度较2005年下降40%至50%的碳减排目标,本文选取中间值45%,得到2020年目标碳排强度。再次,根据2020年GDP预计值,得出2020年的碳排放权总量,即配额总数。最后,选取各地区2012年分别占当年总排放量的比例作为历史分配的依据,从而得到作为投入变量XCO的各地区2020年的碳排放权数量。
(2)GDP及人口数量。首先,考虑各地区经济发展和人口增长的差异性,假定GDP和人口数量分别按各地区自2005年至2012年的平均速率环比增长,得到各地区2020年预期GDP和人口数量。其次,考虑到GDP总量与第二产业GDP之间,总人口与城镇人口之间存在一定的相关性,本文用综合指标法将各地区总人口、城镇人口、总GDP和第二产业GDP四个基础变量归为两项综合变量(人口变量YPOP和GDP变量YGDP)作为产出变量。即将总人口和城镇人口两个变量通过综合指标法归为人口综合变量YPOP,将总GDP和第二产业GDP归为GDP综合变量YGDP。其中综合指标法步骤如下:
3 实证过程与结果分析
3.1 历史分配的效率性水平
运用零和DEA模型对历史分配方法下的各地区效率性水平进行评估,结果如图1。从图1中可以看出:历史分配方法下,各地区零和DEA的效率性水平普遍较低,平均效率水平为0.65。仅江西和广东两省为DEA有效,效率水平值为1。有14个地区的效率值低于平均水平,其中山西、内蒙古、青海、宁夏和新疆等地效率性水平均不足0.4。造成效率值偏低的原因主要为以下三种情况:产出一致或相近时,投入大于其他决策者。
例如山西与吉林在GDP和人口数量上虽然相去不多,但是前者的CO2排放量却是后者的2.7倍;投入一致或相近时,产出却不如其他决策者。例如内蒙古与辽宁相比,前者CO2数量是后者的90%,但其GDP和人口仅为后者的60%左右;产出低于其他地区,投入却高于后者。以青海和宁夏为例,相较于海南,前两者在产出低于后者的同时,投入却大于后者。
3.2 迭代过程及效率性分配结果
从以上初始分配的效率评估结果可知,历史性分配方法并不具有DEA有效性,因而需要采用按比例调整法对以上分配进行调整,并基于调整后的效率性评估结果再进行分配的调整,如此重复数次,直至所有地区达到DEA有效水平,这一过程称之为迭代方法。例如评估得第i个地区的效率性水平为θi<1,为提高其效率水平,需减少CO2排放权X′i=Xi(1-θi),其余地区则分别按各自的CO2排放占总CO2排放的比例增加CO2的排放权。
求得X1BJ值为-14 564 t,调整量为负数说明北京地区自身减少的排放权数量低于其他地区使之增加的数量,因此第一次调整后北京市的排放权较初始分配增加14 567 t。由于每个地区都根据自身的效率水平调整排放权,所以一次调整的结果可能仍无法使所有地区达到DEA有效水平,因而需要进行多次迭代。图2为2020年各地区的迭代过程中,效率水平θ值的变动情况、排放权的调整数量及其占初始排放权数量的比重。其中X轴上方柱状图为地区减少排放权数量,下方为排放权增加数量,每个地区对应的三条柱形分别对应第一次迭代、第二次迭代和第三次迭代结果。折虚线为θ值的变动情况,折实线为排放权总调整数量占初始分配数量的比重。
从θ值的变动情况可以看出,历史分配方法下,即初始分配方案下,除去广东和江西,各地区初始效率值均低于1,未达到DEA有效。因此,根据初始分配效率值进行第一次排放权调整,然后对分配结果进行第二次零和DEA评估,评估结果显示各个地区的效率值均比初始分配效率值更高,但是大部分地区仍未达到效率性水平,进行第二次、第三次迭代后各地区θ值不断上升,但上升幅度逐渐下降,所
有地区经过三次迭代后,都基本达到DEA有效水平,即θ值皆近似为1,因此得到排放权效率性的分配结果。
从CO2的调整量可以看出,各地区CO2排放权均作出了一定程度的调整,且超过半数地区在增加排放权的同时,效率值水平实现了上升。这是因为在零和DEA 模型中,任何一个地区为提高效率值所减少的碳排放权,都以一定的比例增加到其余的地区,即其他地区在产出不变的情况下,增加了投入值,因此造成零和DEA的生产可能性边界位于原始边界的下方, 且随着迭代的进行不断下降。因而即使排放权增加使得地区的绝对效率水平下降,但由于生产可能性边界的下降,其相对效率水平仍然上升。例如江西和广东两省在效率性水平始终为1的情况下,CO2排放权数量却有所增加。而X轴上方柱状图所代表的地区则通过减少排放权实现了效率值的上升,例如河北、山西和内蒙古。这些省市地区的原始排放量均不同程度的超过效率性水平所对应的排放数量,因此根据历次评估的效率性水平,不断削减CO2的排放权数量以达到效率性水平。在三次迭代过程中,全国CO2排放总量保持不变,说明各地区增加与减少的CO2数量总和为零。
从排放权总调整数量占初始分配数量的比重看,广东、江西、山西和内蒙四个地区的调整幅度最大。其中广东省的排放权增加数量相当于原始排放量的62%。这是因为广东地区经济总量和人口基础都远超全国平均水平,凭借其产业结构和技术水平方面的优势,其绝对效率性水
平都远高于大部分地区,因而在排放权大量增加的情况下,仍能保持DEA相对有效。而山西省的排放权减少量相当于原始排放量的约60%。这说明山西省在GDP及人口数量全国排名并不靠前的情况下,由于资源禀赋特征,
导致能源消费结构,即煤炭占能源消费的比重过大,从而使得CO2排放量存在过多的情况。
表2为迭代过程中CO2排放权的分配方案及调整数量。从历次调整总量和排放权总量可以看出,迭代过程中,各地区配额总量保持不变,调整总数量均为零。从最
终排放权分配数量的绝对值看,广东、江苏和山东三个省份CO2排放权数量最多,海南、宁夏和青海三个地区的排放权数量则最少。这都是由各省的经济总量、产业结构、人口因素决定的。其中广东、山东和江苏三省总GDP、第二产业GDP和城镇人口数分别占全国省市地区排名第一、二、三名,总人口数量分别为第一、二、五名;而青海、宁夏和海南的总人口数、城镇人口数及GDP总数在全国各地区间属倒数第一、二、三位。第二产GDP的排名为倒数第二、第三和第一位。因而,从零和DEA的效率性角度,排放权分配数量与地区经济总量和人口数量成正比,即相对效率大致相同的各地区,产出变量值越大,投入量也越大。
4 影响CO2排放效率因素的实证分析
4.1 指标选取及数据描述
(1)经济发展水平。用人均GDP的对数LNGDP来表示。大量研究表明,经济增长是CO2排放的主要原因。王峰等[13]对1995-2007年间中国CO2排放增长率的驱动因素加以分解,并对每一种驱动因素进行了研究,发现在对CO2排放具有正向影响力的因素当中,相对于人口和经济结构等因素,人均GDP的影响程度最大,达到15%以上。同时,薛勇等[14]采用投入产出结构分解方法,对1997-2004年间的CO2排放量变动进行了因素的分解测算,得出的结论同样是经济增长为CO2排放上升的主要驱动力。这说明在我国,CO2的排放数量跟我国的经济发展水平密切相关。
(2)城市化进程。本文将这一因素纳入考察范围,用产业结构、人口结构和固定资产投资结构三个指标衡量。其中,第二产业GDP占GDP的比重RAGDP代表产业结构;城镇人口数占总人口数的比重RAPOP代表人口结构;城镇固定资产投资占全社会固定资产投资比重RAINV代表固定资产投资结构。之所以选取这三个指标,首先,是因为城市化进程的加快势必带来城市规模的进一步扩大,而相应的水泥建材等能源强度高的行业发展也将进一步发展,由此相应的产业结构也将发生变动,为碳减排带来压力;其次,城市的建设必然伴随着农村人口向城市的转移,导致人口结构的变化;最后城镇固定投资比例也代表了城镇化建设进程的速度。
(3)能源消费结构。用原煤消费占能源总消费的比重RAPOW来表示。大量实证研究显示,能源消费结构、产业结构的优化和能源利用效率,与CO2排放数量存在反向变动关系。马晓钰等[15]综合了静态和动态的面板数据模型,根据1999-2010年我国各省市地区的面板数据,对影响中国 CO2排放数量的因素进行了实证研究,结果发现能源消费结构的上升将促进我国 CO2的排放。
(4)技术水平。用能耗强度即能源总消费占GDP的比重RAENE表示。陈诗一[16]指出,从上世纪末到本世纪初,中国的能耗和排放增长得到了显著抑制,单位GDP的能耗和碳排放也持续下降。然而2003年以后中国的重工业化趋势再度显现,随着基础设施建设、房地产汽车行业高速发展、机电化工业出口激增,带来石油金属、建材化工、大型机械设备等重工业的快速成长,能耗的上升带来了CO2排放量的上升。同时,也发现能源强度的降低是CO2排放强度下降的主要直接原因,CO2排放强度减排根本上取决于能源强度的降低或者说能源生产率的提高,与节能减排密不可分。

