砂石料加工废水沉淀池中颗粒絮凝沉降过程模拟研究

李 俊，王 蕾，张晓璐，刘清海，郭 坚，黄冬梅

(1.中国电建集团华东勘测设计研究院有限公司，浙江杭州310014；2.南京慧邦科技研究所，江苏南京210037；3.中国计量大学质量与安全工程学院，浙江杭州310018)

砂石料加工废水沉淀池中颗粒絮凝沉降过程模拟研究

李 俊1，王 蕾1，张晓璐1，刘清海2，郭 坚1，黄冬梅3

(1.中国电建集团华东勘测设计研究院有限公司，浙江杭州310014；2.南京慧邦科技研究所，江苏南京210037；3.中国计量大学质量与安全工程学院，浙江杭州310018)

首先测定某水电站砂石料加工废水处理系统中沉淀池内不同深度处颗粒的粒径分布，在此基础上利用三维无网格扩散限制集团凝聚模型(DLCA)对沉淀池内颗粒絮凝沉降过程进行模拟计算，研究絮凝沉降过程中颗粒分形结构的演化过程。研究结果表明：沉淀池内部颗粒粒径分布较为均匀，颗粒粒径主要集中在30μm左右，中位粒径约为11μm；颗粒沉降时间、沉降颗粒层高度及颗粒层分形维数随初始浓度增大而增大。

砂石料加工废水；沉淀池；分形结构； DLCA；絮凝沉降

0 前 言

沉淀池是砂石料加工废水处理过程中物理处理重要的环节之一，其效率直接影响出水质量及废水处理系统处理效率[1]。沉淀池中细小颗粒在水中时刻不停的做布朗运动，并且在重力作用下克服水的浮力下沉，细小颗粒首先凝聚在一起形成较大的絮团，絮团越大向下的重力越大，下降速度越快，最终沉降[2-4]。在实际砂石料加工废水处理过程中，颗粒絮凝沉降时将形成复杂的絮凝体，然而却很难对其准确观察。随着计算机技术的发展，采用计算机对颗粒絮凝沉降过程进行仿真，观察颗粒絮凝沉降过程中絮凝体的生长过程已成为研究颗粒沉降的主要手段之一。

砂石料加工废水沉淀池中细小颗粒的絮凝沉降过程是一种典型的分形生长现象[5-6]。目前采用计算机模拟对其进行研究主要是基于扩散限制凝聚(DLA)或扩散限制集团凝聚模型(DLCA)。DLA方法假设颗粒存在一个凝聚中心，随机释放的粒子向凝聚中心运动，不能模拟颗粒的随机运动及沉降，其模拟结果与实际情况相距甚远。DLCA假设初始条件下，颗粒随机分布，不设置固定中心，允许模拟空间内颗粒和絮凝体随机运动，形成颗粒更多、尺度更大、内部结构更复杂的絮团。因此更接近于实际水中的絮凝沉降过程[7-11]。然而由于传统三维DLCA计算需求巨大，因此目前主要集中在采用二维DLCA进行模拟计算。

本研究以某水电站砂石料冲洗废水处理过程中沉淀池为研究对象，首先测定不同高度处沉淀池内颗粒粒径分布，基于试验测定结果，采用三维无网格DLCA模型，对沉淀池内颗粒絮凝沉降过程进行模拟计算，观察其分形生长过程。颗粒絮凝沉降过程一方面进行随机布朗运动，另一方面在重力作用下下沉，当计算区域中所有颗粒均沉降到底部，计算结束。

1 絮凝沉降过程计算机模拟

采用三维无网格DLCA对絮凝沉降过程进行模拟计算。模拟过程中粒子进行无规则布朗运动，颗粒布朗运动位移采用爱因斯坦布朗运动位移公式计算，如下[11]：

(1)

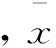
颗粒在进行布朗运动的同时，由于自身重力的作用，将克服水的浮力而不断沉降。假设在沉淀池泥沙沉降过程中水处于静止状态，则本研究采用层流区重力沉降公式计算水中颗粒沉降位移[11]：

(2)

式中，d为絮凝体直径，m；ρs为颗粒密度，kg/m3；ρ为水的密度，kg/m3；g为重力加速度，9.81 m/s2；μ为水在温度T时的运动粘度，m/s2。

计算开始时，根据水中颗粒浓度，产生N个互不重叠，直径为d的颗粒。任取某一絮凝体或颗粒进行随机布朗运动及重力沉降，当絮凝体或颗粒与其他絮凝体或颗粒发生碰撞后，与碰撞颗粒形成新的絮凝体，不再分离，直到计算区域中所有颗粒均沉降到底部，计算结束。模拟计算过程中，颗粒直径根据测定结果确定，计算时间步长为1 s，计算区域为200×200×200，计算区域内粒子数采用如下公式计算[12]：

(3)

式中，c为粒子浓度；L为计算区域尺度。

对于颗粒群，有如下关系[13]：

(4)

两边取对数，得：

(5)

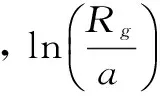
2 结果与讨论

2.1 沉淀池中颗粒粒径分布

本项目中设计的沉淀池容积为150 m3，废水在沉淀池中水力停留时间约1.4 h，沉淀上清液进入调节池。沉淀池配置有1台链式刮泥机，间歇式运行，定期将沉淀池中的污泥刮出至振动脱水筛进行泥水分离。沉淀池中料浆固体含量的体积分数为15%～20%，固体量为14 t/h，料浆量为70～95 m3/h。采用激光粒径分析仪测定0.3 m和0.7 m高度处颗粒粒径分布。测试结果如图1所示。由图1可知，沉淀池两处颗粒粒径分布差别甚微，颗粒中位粒径分别为10.14、11.91 μm。颗粒粒径主要分布在0.2～100 μm之间，最大粒径和最小粒径分别约为95、0.2 μm。颗粒粒径较为均匀，颗粒粒径分布近似成偏正态分布，体积分数为80%的粉体粒径小于30 μm，占总体积最多的颗粒粒径为17～29 μm。

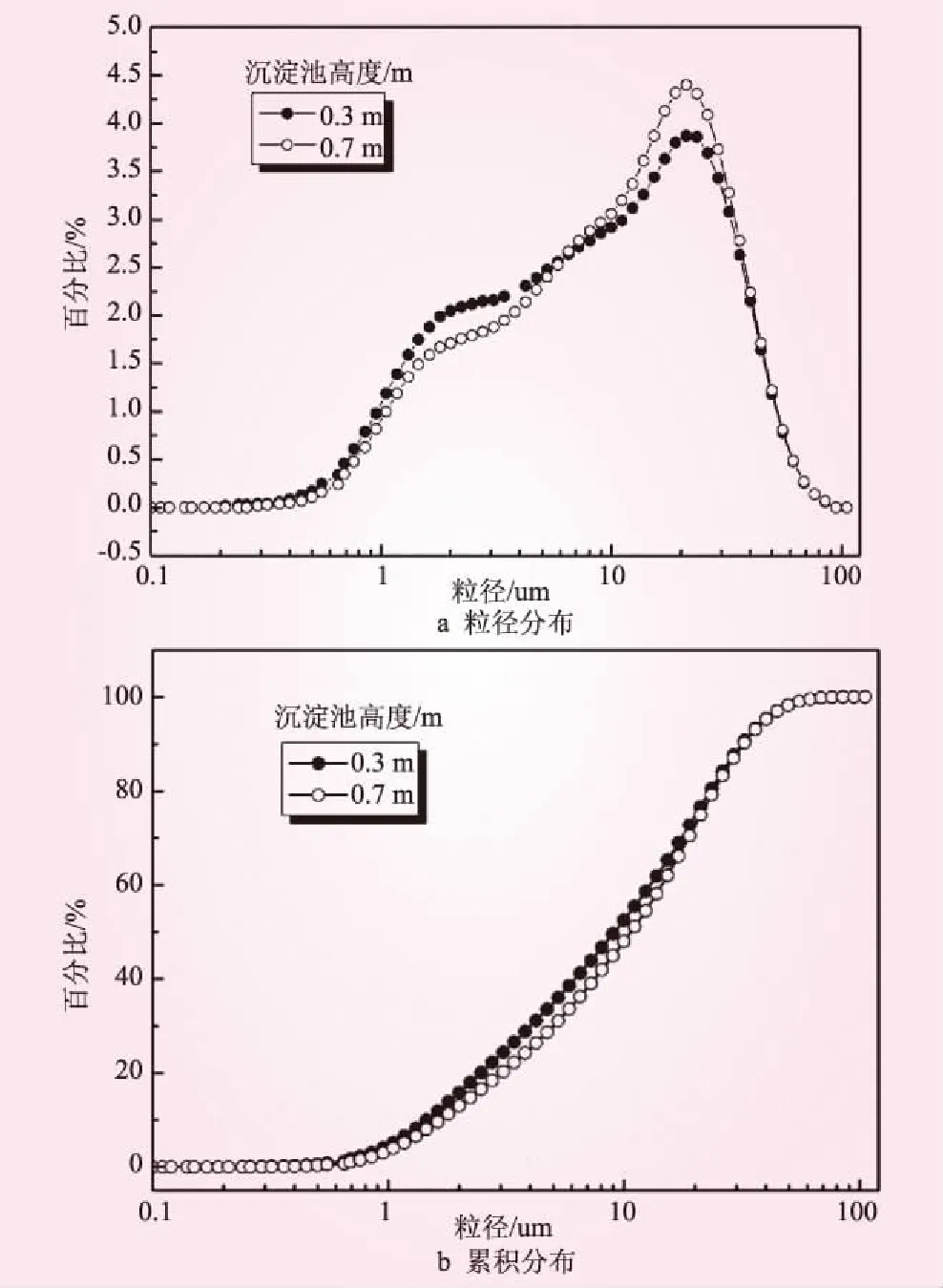
图1 沉淀池不同高度处粒径分布

2.2 模拟结果分析

模拟计算中颗粒直径取11 μm，初始状态下颗粒在计算区域中随机分布，计算区域内介质为水，初始温度为293 K，计算体积分数为5%、8%、10%、12%、15%、20%、25%，初始粒子数为574、919、1 149、1 378、1 723、2 297、2 871。计算结束后记录颗粒沉降时间，沉降颗粒层厚度及分形维数。体积分数为5%时，不同时刻颗粒絮凝体形貌如图2所示。由图2可知，初始时刻颗粒随机分布于整个计算区域内部，随着布朗运动和重力沉降的进行，颗粒碰撞，首先由多颗粒形成小絮凝体，絮凝体较之单个颗粒体积增大，质量增大，而使其重力沉降速度加快，从而使絮凝体不断下沉，288 s时刻颗粒主要集中在150 μm以下，588 s时刻，颗粒继续沉降，颗粒主要集中在100 μm以下，至616 s，颗粒全部沉降至底部，泥沙高度约为80 μm。在整个沉降过程中，颗粒相互碰撞凝结，加速颗粒沉降速度。

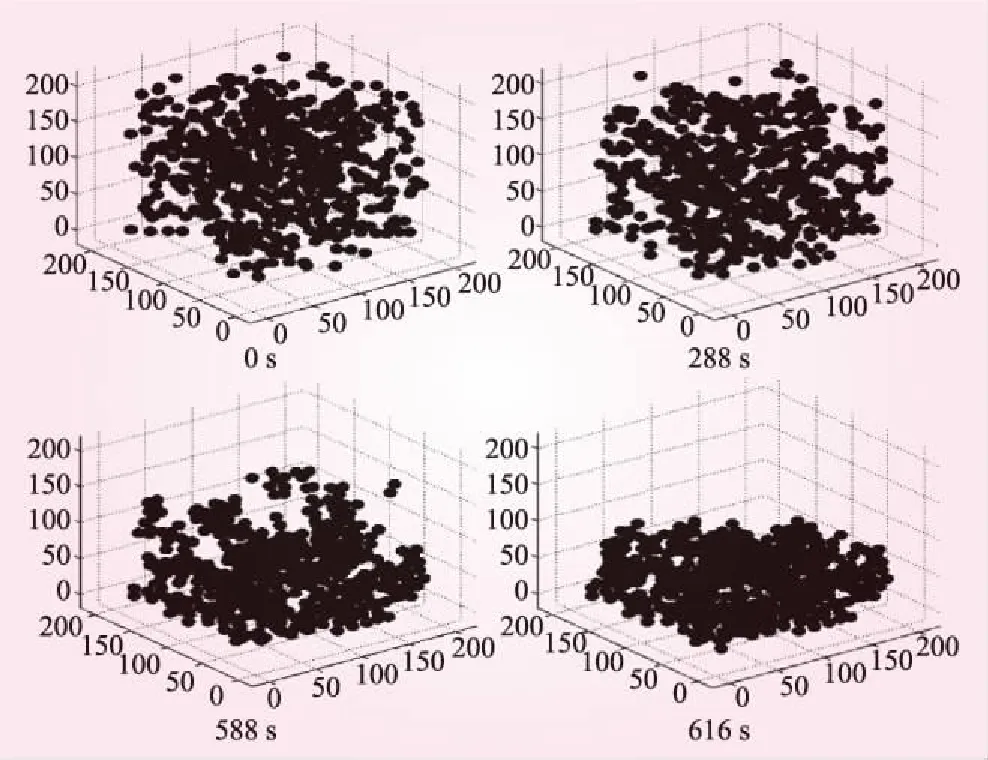
图2 体积分数5%时絮凝体形貌

由对沉淀池中颗粒粒径分布的测定可知，沉淀池中颗粒的体积分数80%的颗粒粒径小于30 μm，占总体积最多的颗粒粒径为：17～29 μm。悬浮颗粒在水中做布朗运动和重力沉降过程中碰撞形成絮凝体，絮凝体不断增大，做整体运动，由于絮凝体体积不断增大，最终在重力的作用下，絮凝体将沉降至底部，这些絮凝体形成的结构是典型的分形结构，沉降结束后，絮凝体的分形维数采用式(4)计算，颗粒体积分数15%时，分形维数计算如图3所示。由计算可知，颗粒沉降结束后，形成的絮凝体分形维数Df为1.567 42，参数k0为-0.189 09。

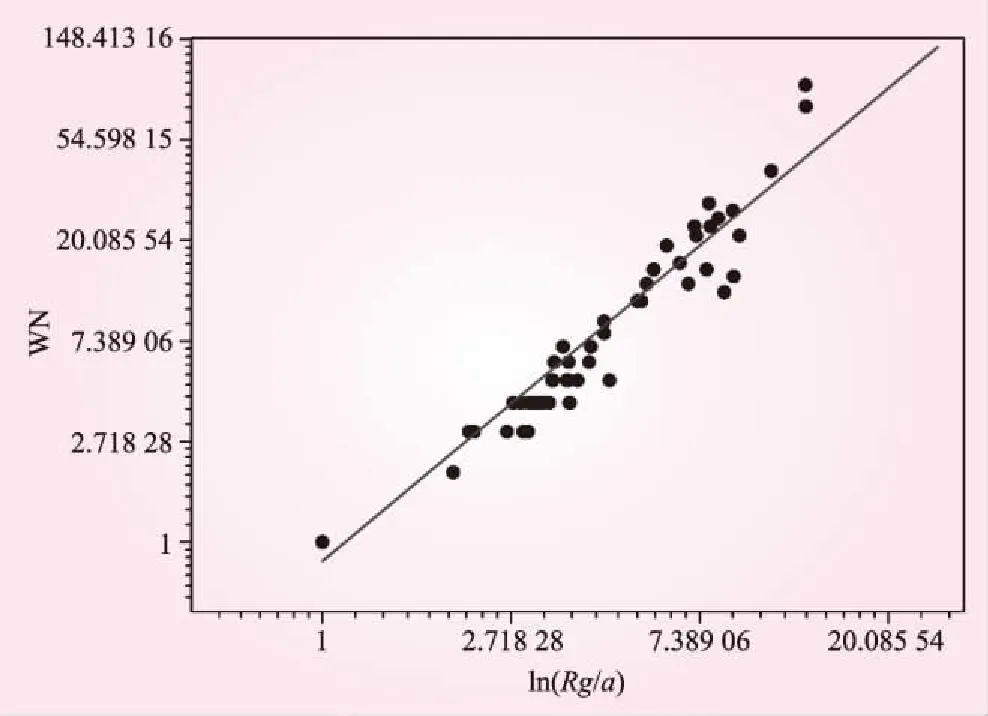
图3 体积分数15%时分形维数

采用同样的方法计算，得出颗粒体积分数从5%～25%时，颗粒完全沉降时间，絮凝体高度，颗粒层分形维数。颗粒沉降时间与颗粒高度随体积分数变化曲线如图4所示，由图4可知，随着体积分数的增大，所需沉降时间不断增加，沉降时间与颗粒体积分数呈线性关系增加，由最小二乘法拟合可得本文计算条件下颗粒沉降时间(T)与体积分数(c)的关系为T=90.74+108.17c。由图4可知沉降结束后，颗粒高度随体积分数的增大而增加，当计算区域内颗粒体积分数较低时，沉降结束后，出现明显的颗粒区和清水区，上层较大区域内不存在颗粒，随着体积分数的增大，颗粒和水的界面不断上移，当颗粒体积分数大于20%时，颗粒高度大于180 μm，即当颗粒初始体积分数大于20%时，沉降后颗粒基本充满了整个计算区域。

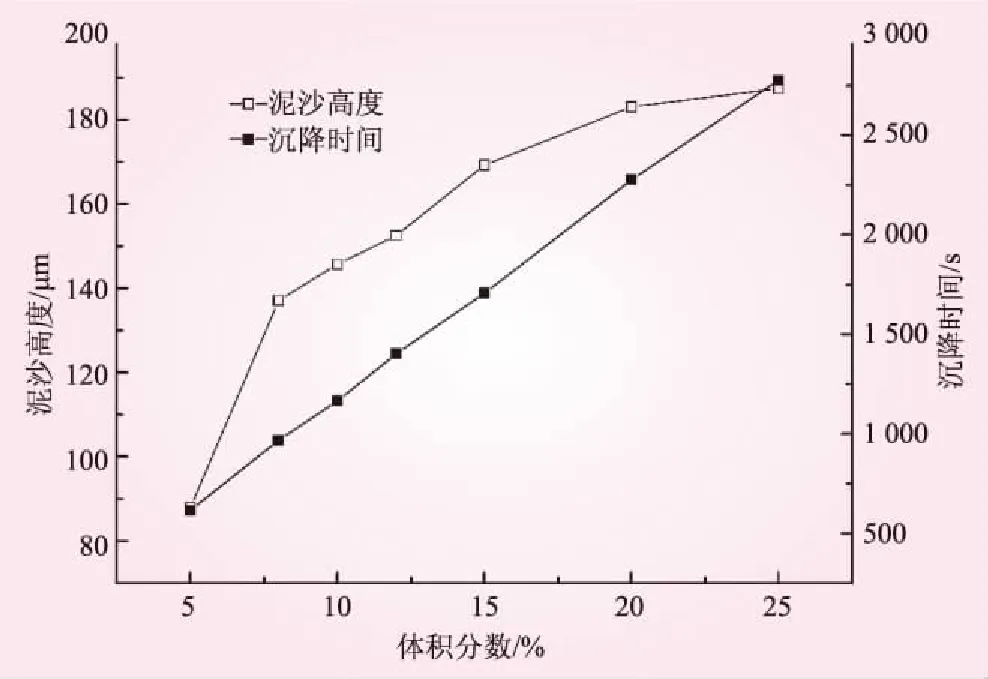
图4 颗粒沉降时间与颗粒高度随体积分数变化曲线

图5为计算结束后，颗粒絮凝体分形维数随体积分数变化曲线。由图5可知，颗粒絮凝体分形维数Df随体积分数的增大而增大。这是因为当计算区域内颗粒体积分数增大时，颗粒数增多，颗粒在布朗运动和沉降过程中碰撞几率增大，使得形成的絮凝体颗粒数增多，体积增大，最终形成的絮凝体密实、结构更加复杂。此计算结果与文献[11]结果一致。

图5 分形维数随体积分数变化曲线

3 结 论

本研究首先测定某砂石料加工废水沉淀池中0.7 m和0.3 m高度处颗粒粒径分布，基于粒径分布的结果，采用三维无网格DLCA模拟沉淀池中颗粒絮凝沉降过程，颗粒在沉降过程中主要为布朗运动和重力沉降。模拟结果能够形象的反应沉淀池中颗粒悬浮体系的絮凝沉降过程，所得结论如下：

(1) 由粒径分布测定结果可知，颗粒粒径主要集中在30 μm左右，中位粒径约为11 μm，沉淀池0.7 m和0.3 m高度处颗粒粒径无明显差异，该沉淀池中砂石料加工废水的颗粒比较均匀；

(2) 在沉降过程中，颗粒首先形成小的絮凝体，小的絮凝体继续运动，不断碰撞其他颗粒或絮凝体，絮凝体体积不断增大，从而使絮凝体向下沉降速度

加快，最终完全沉降到计算区域底部，所需沉降时间和沉降颗粒层高度随颗粒初始体积分数增大而增大；

(3) 采用DLCA计算得到的颗粒层絮凝体为分形结构，分形维数随颗粒初始体积分数增大而增大，初始体积分数越大形成的絮凝体结构越复杂，絮凝体越致密。

[1]蔡金傍， 段祥宝， 朱亮. 沉淀池水流数值模拟[J]. 重庆建筑大学学报， 2003， 25(4)： 64-69．

[2]蒋卫刚， 顾国维， 俞国平. 二沉池动态仿真模型研究[J]. 环境工程学报， 2007， 1(3)： 21-24．

[3]聂德明. 颗粒沉降及其在流场中做布朗运动的研究[D]. 杭州： 浙江大学， 2011．

[4]曾光明， 葛卫华. 污水厂二维沉淀池水流和悬浮物运动数值模拟[J]. 中国环境科学， 2002， 22(4)： 338-341．

[5]郭航. 水中絮凝体分形成长动态仿真技术研究[D]. 哈尔滨： 哈尔滨工业大学， 2012．

[6]李冬梅， 梅胜， 谭万春， 等. 黄河泥沙架桥絮凝体分形结构的动态演变研究[J]. 给水排水， 2005， 30(11)： 1-5．

[7]蒋新. MATLAB 平台上的 DLCA 过程模拟[J]. 计算机仿真， 2003， 20(6)： 68-70．

[8]刘东京， 邱祖民. 反应概率置限二维 DLCA 模型分形模拟[J]. 计算机与应用化学， 2012， 29(4)： 451-453．

[9]齐灿， 吴世先. 应用 DLCA 模型模拟超细气溶胶粒子的凝并行为[J]. 桂林航天工业高等专科学校学报， 2008， 13(2)： 31-34．

[10]温娟， 李宏， 王万军， 等. 应用 DLCA 模型对钢水中夹杂物粒子集团凝聚过程动力学行为的模拟研究[C]∥冶金研究中心 2005 年“冶金工程科学论坛” 论文集， 2005．

[11]杨铁笙， 李富根， 梁朝皇. 粘性细颗粒泥沙静水絮凝沉降生长的计算机模拟[J]. 泥沙研究， 2005(4)： 14-20．

[12]JULLIEN R， OLIVI-TRAIN N， HASMY A， et al. Scaling theory and numerical simulations of aerogel sintering[J]. Journal of non-crystalline solids， 1995， 188(1)： 1-10．

[13]MEAKIN P. Formation of fractal clusters and networks by irreversible diffusion-limited aggregation[J]. Physical Review Letters， 1983， 51(13)： 1119．

(责任编辑 王 琪)

Simulation of Flocculation-Sedimentation Process in Clarifier of Wastewater from Sand and Gravel Processing

LI Jun1, WANG Lei1, ZHANG Xiaolu1, LIU Qinghai2, GUO Jian1, HUANG Dongmei3

(1. PowerChina Huadong Engineering Corporation Limited, Hangzhou 310014, Zhejiang, China;2. Nanjing Huibang Institute of Technology, Nanjing 210037, Jiangsu, China;3. College of Quality and Safety Engineering, China Jiliang University, Hangzhou 310018, Zhejiang, China)

The particle size distribution at different height of clarifier is firstly measured by using laser particle size analyzer, and then a three dimensional mesh free diffusion limited cluster aggregation model (DLCA) is developed to simulate the flocculation settling process of particle in clarifier. The evolution of floc fractal is analyzed. The results indicate that, (a) the particle size uniformly distributes in clarifier and mainly concentrates in about 30 μm, and the median value is about 11 μm; and (b) with the increase of initial particle concentration, the sedimentation time, particle bed height and fractal dimension are increased．

Waste water from sand and gravel processing; clarifier; fractal structural; DLCA; flocculation-sedimentation

2016-01-06

李俊(1983—)，男，四川广元人，工程师，硕士，主要从事水利水电工程环保设计、环境影响评价工作．

X703

A

0559-9342(2016)11-0106-04