基于激光追踪仪的精密转台角度标定方法*
白普俊 薛娜 刘松涛 宋涛 李金和
(1.天津大学 机械工程学院, 天津 300072; 2.辰星(天津)自动化设备有限公司技术部, 天津 301701)
基于激光追踪仪的精密转台角度标定方法*
白普俊1薛娜1刘松涛2†宋涛2李金和1
(1.天津大学 机械工程学院, 天津 300072; 2.辰星(天津)自动化设备有限公司技术部, 天津 301701)
摘要:针对一类大直径精密转台不易采用传统方法实现高精度角度测量的问题,提出了一种基于激光追踪仪空间位置坐标测量的单自由度转台旋转角度的测量和补偿方法.首先依据“不共线的三点确定一个圆”的几何原理,建立了被测点空间位置坐标信息与转台角度之间的映射关系,并分析激光追踪仪的位置测量精度对转台角度测量精度的影响,据此提出了被测点半径长度和测量角度间隔的选取原则,以期充分利用激光追踪仪的位置测量精度实现转角误差的高精度测量;然后利用多项式插值方法获得转台转角误差随转角位形的变化规律,并将误差拟合为补偿函数嵌入控制器中,采用修正光栅输出示数的方式来实现转角误差的实时补偿.将文中方法实施于1台安装有圆光栅的精密转台的标定实验中,结果表明,文中方法可有效校正由圆光栅装配误差导致的角度定位误差,使其由标定前的40″降低至5″.
关键词:精密转台;光栅测量;标定;激光追踪仪
近年来,一类直径在1~3 m的精密大型工作转台在工业生产和试验环节得到了广泛的应用[1- 6],该类工作转台可实现对大体积、大质量工件的旋转角度的高精度测量或者高精度定位.目前,依据测量原理的不同,转台角度的测量主要有3种实现方式:①机械式测角技术[7],通常采用多尺分度盘结构,但由于多尺分度盘的齿数不能无限地增加,使其角度测量精度受到较大的限制;②电磁式测角技术[8-10],主要有磁栅测角和感应同步器测角,但在大量程测量时其分辨率和精度较低;③光学测角技术[11-17],常用方法有光学分度头法、多面棱体法、光电编码器法、自准直法、莫尔条纹法、平行干涉图法、圆光栅法、激光干涉法、环形激光法及机器视觉法等,上述方法因具有极高的测量精度而在测量领域得到广泛的应用.其中,圆光栅测量的输出信号为数字脉冲,具有检测范围大、检测精度高、响应速度快、抗干扰能力强等优点,已逐渐发展成为高精密转台角度测量输出的标配部件.然而,由于大口径圆光栅与转台的装配过程中存在同轴度误差及变形和扭曲,并且光栅读数头与圆光栅也存在距离、俯仰和扭转误差,导致圆光栅实际转角测量的失真,使其不能满足高精度应用场合的需求,因此,必须采取有效措施予以校正.在实际工程中,可以采用两种方法来改善转台的转角定位精度:①提高转台系统的机械加工精度,采用精密的装配校准工艺以严格控制光栅的装配精度[18-19],实现转台转角定位精度的提升,但该方法将增加基础零部件的加工和装配难度,导致成本增长,而且由于加工和装配误差不可能绝对消除,故该方法对转台转角定位精度的改善程度受到制约;②光栅角度标定[20-21],即利用高精度测量手段获取转台转动角度真值与光栅示值之间的误差,并将此误差补偿至控制器中,从而实现转台角度误差的校正.然而,光栅自身的测角精度很高,要实现对带有光栅测量系统的转台转角的直接测量,则需要具有更高精度的角度测量设备.然而,对于大直径转台而言,非常不利于诸如多面体棱镜等角度测量仪器的精确安装,并且此类角度测量仪器受人为因素的影响较大,故该方法存在成本昂贵且实施困难等问题.
针对上述问题,文中提出了一种基于激光追踪仪空间位置坐标信息检测的单自由度转台旋转角度的测量和补偿方法.首先,建立被测点空间位置坐标信息与转台角度之间的映射关系,分析激光追踪仪的位置测量精度对转台角度测量精度的影响,并据此提出被测点半径长度和测量角度间隔的选取原则;然后,利用多项式插值方法获得转台转角误差随转角位形的变化规律;最后,采用修正系统输入的方式将误差拟合为补偿函数嵌入控制器中,以实现转角误差的实时补偿.
1系统描述
如图1所示,文中研究的精密转台由伺服电机、减速机、小齿轮、大齿轮、转动平台、转盘轴承、支架、圆光栅和光栅读数头等主要部件组成.转动平台通过精密转盘轴承与支架连接,可实现绕自身轴线的单自由度转动.伺服电机通过减速机驱动小齿轮转动,小齿轮与固接于转动平台的大齿轮啮合,从而驱动转动平台运行.圆光栅通过连接环与转动平台同轴固接.当圆光栅随转动平台同步旋转时,安装在支
架上的光栅读数头通过测量圆光栅转过的栅线数来获取转动平台的旋转角度,从而实现对大体积、大质量工件的旋转角度的高精度测量或定位.
2总体方案
角度定位精度是精密转台的主要特征参数之一.依据图1描述的转台的构造易知,转台的转动角度是利用圆光栅测量的.然而,由于加工和装配误差的不可避免,使转台转角的真值与光栅示值之间存在误差.为此,文中利用光栅角度标定方法来提高转台的转角定位精度.圆光栅的角度标定涉及两方面的内容:①角度误差测量,即利用激光追踪仪测量被测点转过一定角度时的空间坐标,通过空间点坐标与转动角度的数学关系计算得到转动真值,并与光栅示值求差计算角度误差;②角度误差补偿,即利用多项式插值原理,将角度误差拟合为关于转角位形的函数嵌入控制器中,采用修正光栅输出示数的方式来实现转角误差的实时补偿.
3角度测量的数学基础
如图2所示,被测点P至转台回转中心O′的距离为R,Pi(i=1,2,…,n;n≥3)为转台转动一定角度φj(j=1,2,…,n-1)时被测点P的空间位置测量点,θk(k=1,2,…,n-2)为转台的转动角度真值.i、j、k满足如下关系:
(1)
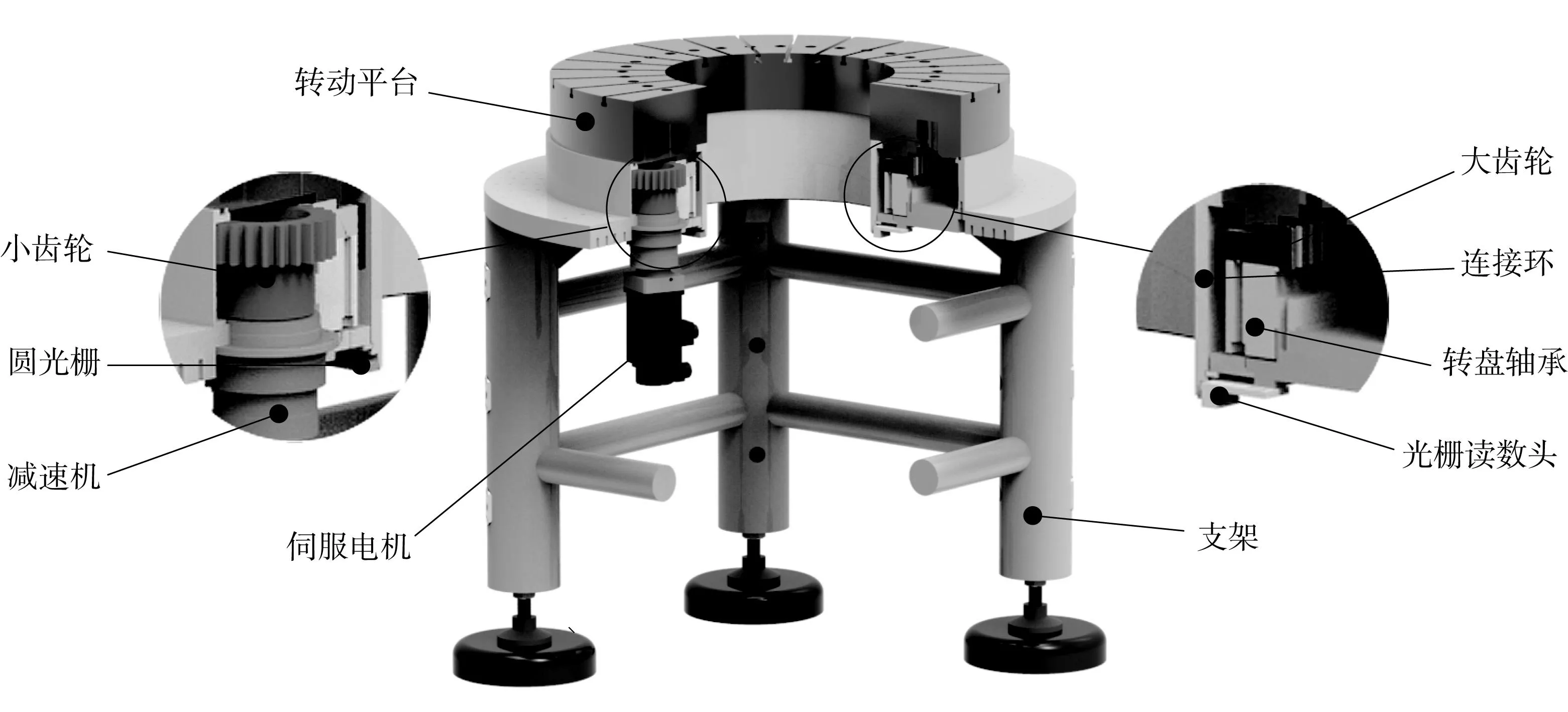
图1 转台模型Fig.1 Model of rotating platform
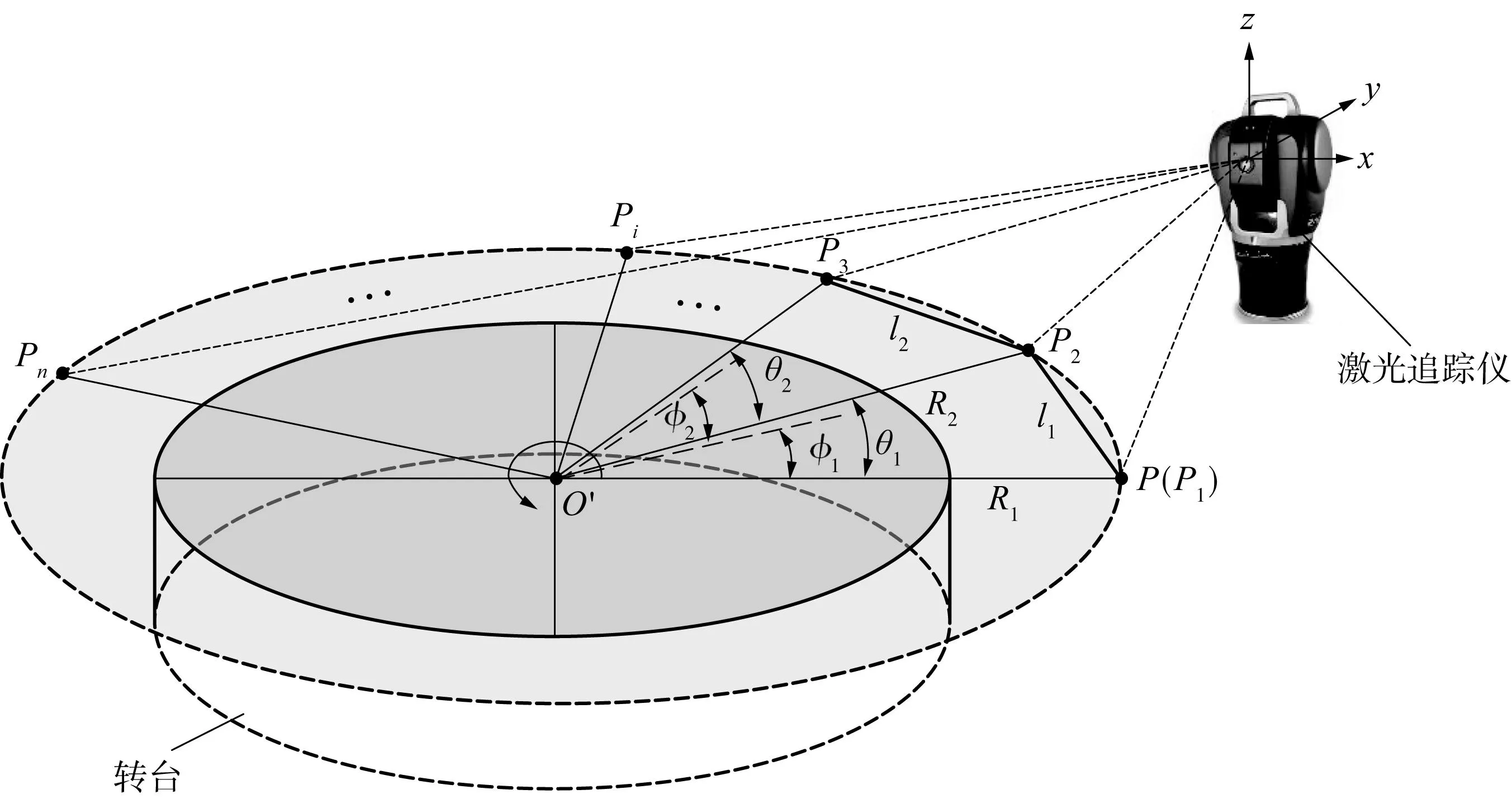
图2 位置-角度测量原理图Fig.2 Principle of position-angle measurement
Ax+By+Cz+1=0
(2)
式中,A=(-ykzk+1+yk+1zk+ykzk+2-yk+2zk-yk+1zk+2+yk+2zk+1)/S,B=(xkzk+1-xk+1zk-xkzk+2+xk+2zk+xk+1zk+2-xk+2zk+1)/S,C=-(xkyk+1-xk+1yk-xkyk+2+xk+2yk+xk+1yk+2-xk+2yk+1)/S,S=xkyk+1zk+2-xkyk+2zk+1-xk+1ykzk+2+xk+1yk+2zk+xk+2ykzk+1-xk+2yk+1zk.
设相邻3点Pk、Pk+1、Pk+2确定的空间圆的圆心即转台瞬时回转中心O′的坐标为(uk、vk、wk),易知圆心O′在式(2)描述的平面内,根据圆的特征可确定方程组求解
(3)
计算求得由空间3个相邻被测点确定的空间圆的圆心坐标为
(4)
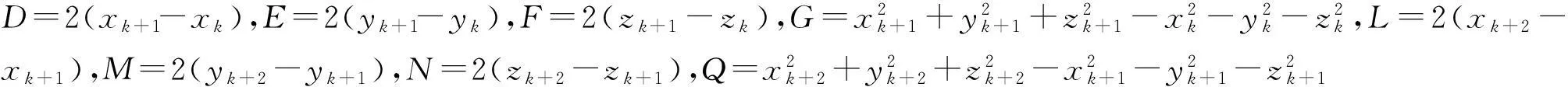
进而可求得空间圆的半径为
(5)
通过三角形余弦公式,计算求得转台转动的真实角度为
(6)

4误差补偿
在误差补偿环节,文中将测量计算有限个角度误差,利用多项式插值原理,通过拟合误差函数曲线间接求得圆光栅整圈误差的近似分布规律.图3示出了转动角度真值的计算流程,主要分为3个步骤:①伺服电机驱动转台复位至光栅零点位置,设定被测点P的初始位置和转台转动角度φj;②依据程序预设控制伺服电机驱动转台转动角度为φj,然后记录被测点的空间坐标(每个空间点坐标测量3次取平均值)和光栅读数头的角度示数αj;③将被测点空间坐标代入式(3)-(6),计算求得真实转动角度θk和转动半径Rk.
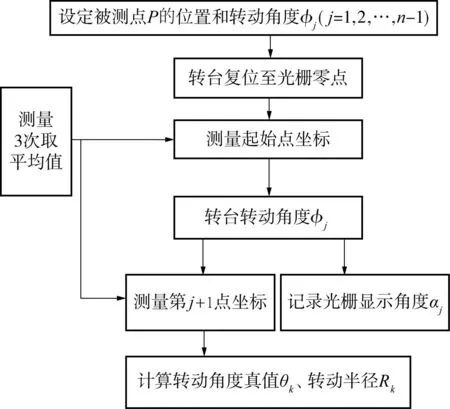
图3 转动角度真值计算流程图Fig.3 Calculation flowchart of real rotation angle
考虑到光栅显示的角度值为转台累计转动角度,故离散的角度误差可表示为
(7)
利用最小二乘法将通过式(7)计算求得的离散角度误差进行多项式拟合,即可获得角度误差关于光栅角度示数的多项式函数
Δγm=f(α)=amαm+am-1αm-1+…+
a1α+a0,m≥2
(8)
式中:α为光栅示出的瞬时角度值;Δγm为光栅在瞬时角度值时的角度误差;a0,a1,…,am为多项式函数的常数系数.
利用式(8)可计算求得转台转动任意角度时的近似光栅角度示数误差.因此,光栅的角度示数可修正为
φ=α+Δγm
(9)
式中,φ为修正后的光栅角度示数.
5实例分析
5.1 参数设定
文中使用型号为Leica AT901-LR的激光追踪仪,其性能参数如下:测量6.5 m远处1 400 mm标准空间长度的组合不确定度应小于等于0.024 mm,绝对距离测量(ADM)全工作量程下的测量不确定度应小于0.005 mm,可信度均为2σ.由于激光追踪仪的空间位置和长度测量精度与测量距离的远近和被测长度的长短相关,因此,根据激光追踪仪的测量精度选择合适的被测点,是文中所述角度补偿方法的关键.依据式(6)易知,文中所述测量方法需注意两个参数的选择:①被测点与转台回转中心之间的距离Rk,依据激光追踪仪空间点位置测量精度确定一个合理的被测点,以尽可能降低空间点坐标测量误差引起的半径误差对真实角度计算的影响;②转台转动角度φj,转台转动角度决定了由被测点坐标误差导致的弦长误差对真实角度的影响.
为了确保测量精度,设定测量范围在以激光追踪仪为中心的6.5 m以内,且lj≤1 400 mm.按照最恶劣的条件,可设定激光追踪仪测量的空间点位置误差导致的被测点与回转中心的最大距离误差ΔRmax=0.024 mm,最大弦长误差Δlmax=0.024 mm.因此,由空间点坐标测量误差引起的最大角度误差为
Δγmax,j=γmax,j-γmin,j
(10)
式中,γmax,j和γmin,j分别为考虑空间点测量误差时可能计算得到的转台转动角度的最大值和最小值,
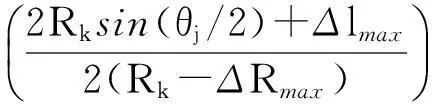
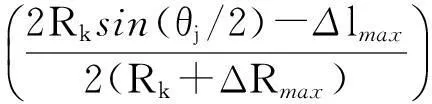
依据式(10)可获得转台转角最大误差Δγmax,j与转角θj和距离Rk之间的关系,如图4所示.

图4 转台最大转角误差Fig.4 Maximum rotating angle error of rotating platform
考察图4可知,被测点P距离转台回转中心越远,每相邻两点间转动角度越小,空间点测量误差导致的最大角度计算误差越小.然而,Rk越大,则实验所需的空间和场地越大,且转动角度越小所需被测点越多,降低了实验效率.因此,同时考虑空间限制和合理的实验时间,在保证转台测量精度控制在5″以内的前提下,设定测量条件为
φj=10°,1 400 mm≤Rk≤1 500 mm
(11)
此外,依据光栅测量的原理易知:①当光栅旋转一周时,光栅角度示数为360°,即无论在转动过程中角度示数误差如何,经历整周后的显示角度值是固定的;②光栅与转台装配完成后,光栅在任意位置的示数误差都是固定的,即光栅的示数误差仅与其转角位置有关,与转动圈数无关.基于上述事实,仅需测量光栅一圈内的角度误差,即可拟合光栅的角度误差函数.因此,基于式(11)设定的测量条件,设定n=37,则式(8)可改写为
Δγm′=f(ψ)=amψm+am-1ψm-1+…+
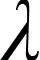
(12)
5.2 误差补偿实验
依据前面设定的测量条件,搭建基于激光追踪仪空间位置坐标检测信息的转台角度测量实验平台,如图5所示.为增加被测点的径向距离,利用一根延长钢柱与转动平台固定,以便将激光测量靶球放置于式(11)设定的区间内.控制系统发出指令控制伺服电机驱动转台间歇转动,利用激光追踪仪依次测量被测点的空间坐标,并代入式(2)-(7),即可求得角度误差Δγj和回转半径Rk(见图6、7).此时,将外部固定的杠杆千分表与转动平台的内部基准孔面接触并预留适当的压缩量,依次记录各测点位形下千分表的读数,最终以初始测点为参考,获得的同轴度误差分布如图8所示.

图5 空间点坐标测量实验平台Fig.5 Experimental setup of space point coordinate measuring
从图6-8可知:①角度误差和被测点回转半径3次实验具有良好的重复性;②被测点回转半径的波动规律与转台的同轴度误差正相关,即Rk的波动主要是由转动平台与回转轴承的同轴度误差引起的,空间点坐标测量误差对半径精度的影响甚小,间接说明了激光追踪仪的空间点位置测量误差对真实角度计算影响甚微.这表明文中所提出的角度测量方法是有效的,可以作为试验过程中测量数据可靠性的判定依据.
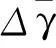
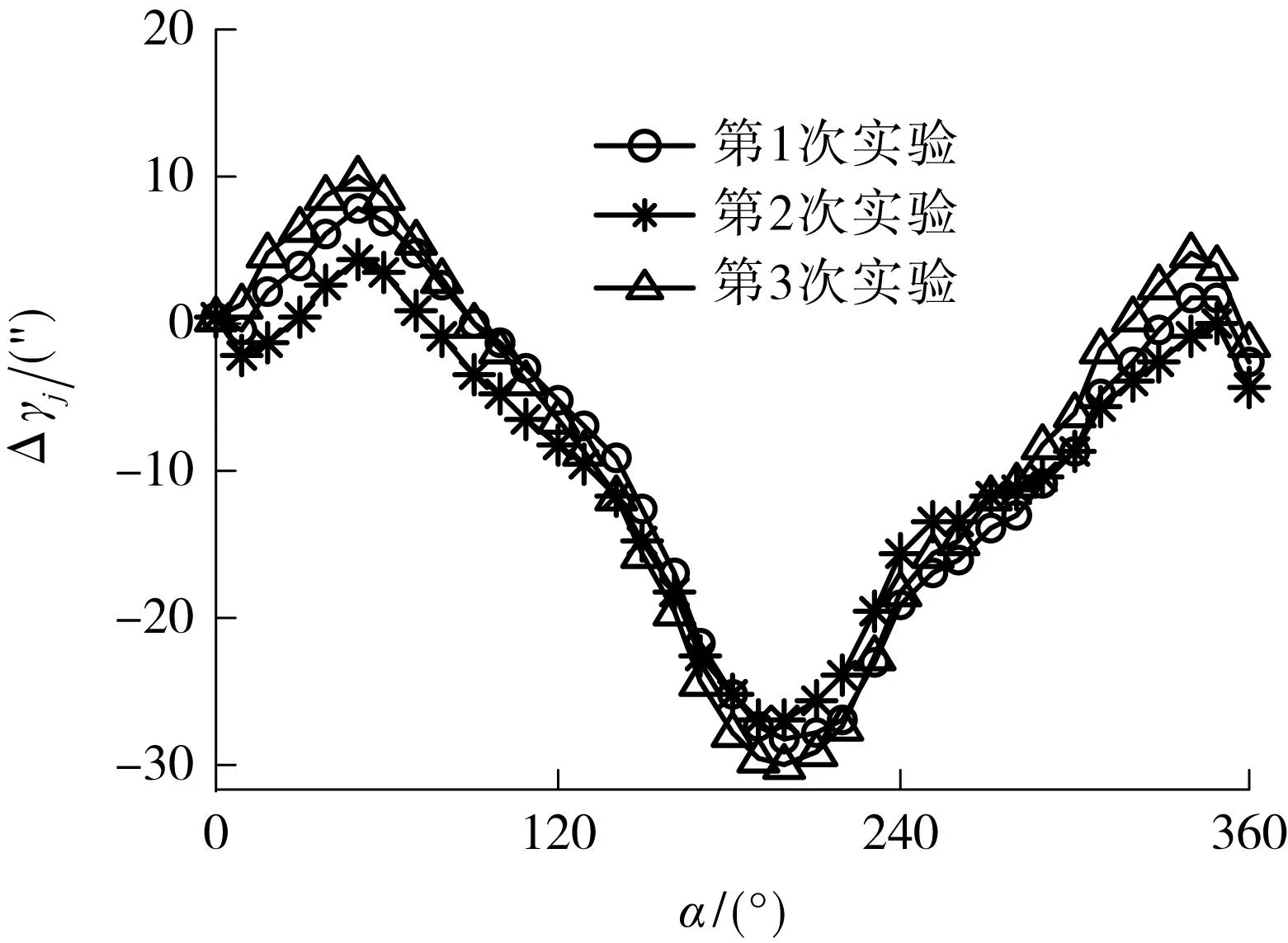
图6 离散光栅角度测量误差Fig.6 Discrete grating angle measurement error
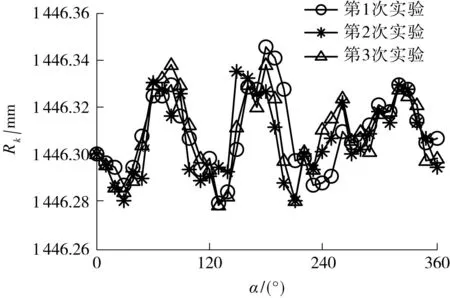
图7 回转半径分布图Fig.7 Distribution of gyration radius
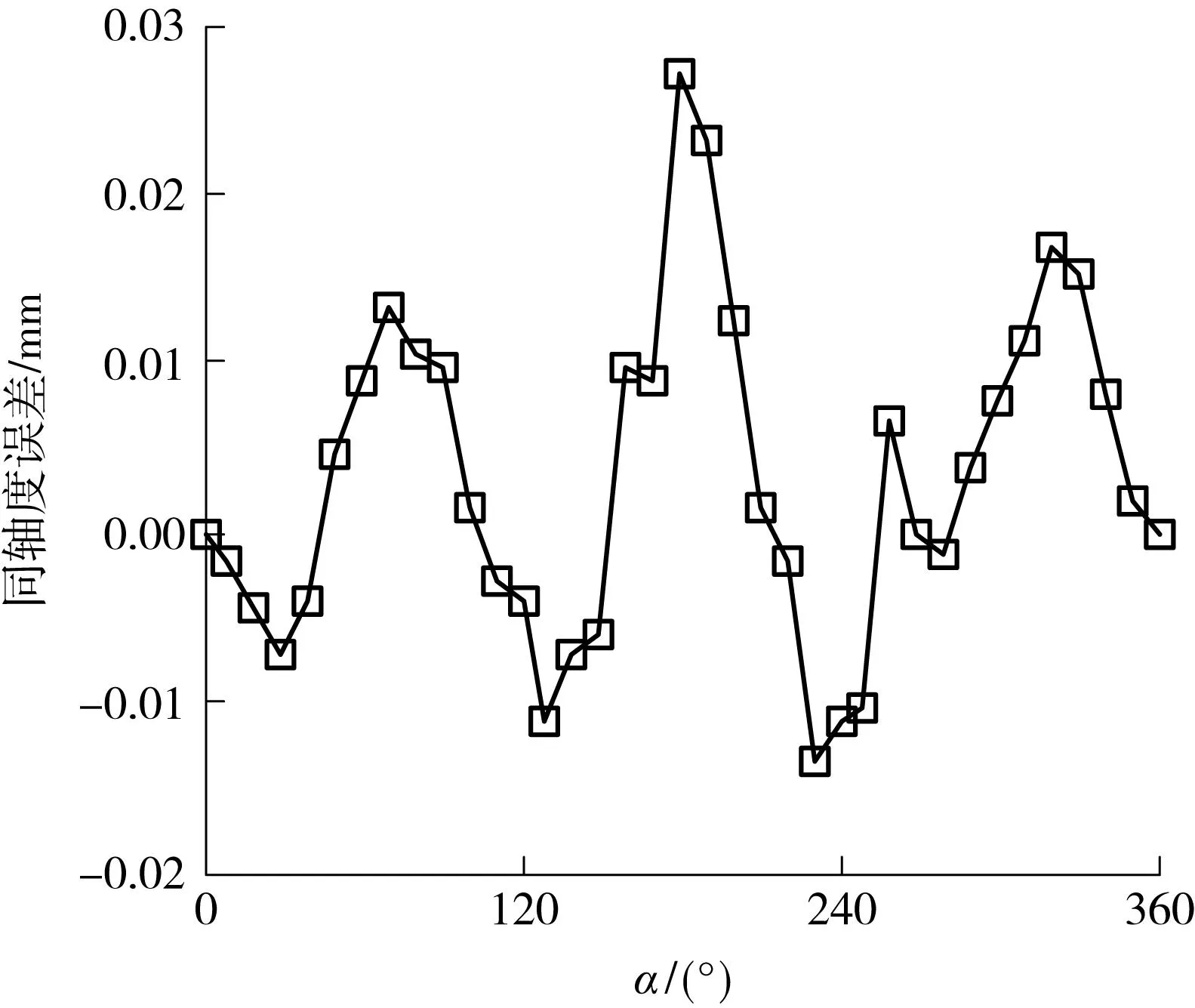
图8 同轴度误差分布图Fig.8 Distribution of coaxiality error
φ′=α+Δγ4′
(13)
式中,Δγ4′=a4ψ4+a3ψ3+a2ψ2+a1ψ+a0.
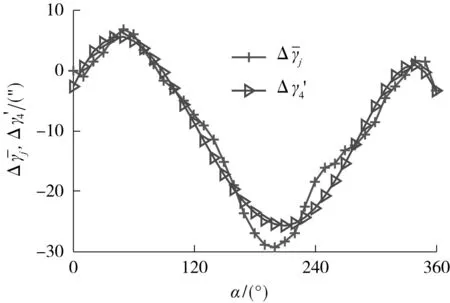
图9 角度误差多项式拟合曲线Fig.9 Polynomial fitting curves of angle error

φ″=φ′+Δγ4″
(14)

第2次补偿后,再次利用激光追踪仪进行验证测量,计算角度误差如图10(c)所示.转台角度误差补偿前后的最大角度误差见表1.结果显示,经过两次误差补偿,标定后的转台实际转角值与光栅示值之间的误差可被控制在5″以内,充分验证了文中所提出的标定方法的有效性.
表1补偿前后误差比较
Table 1Error comparison before and after compensation
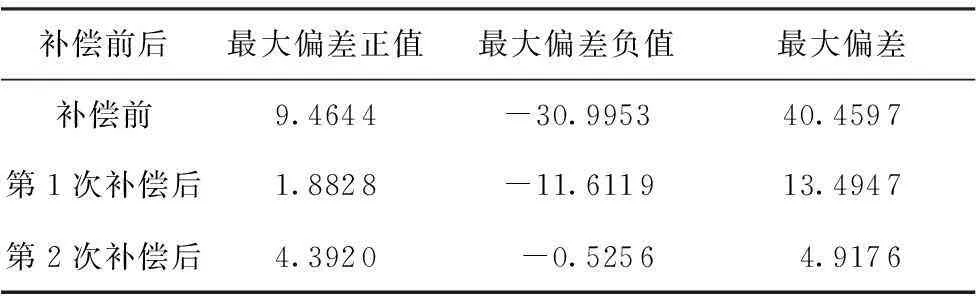
补偿前后最大偏差正值最大偏差负值最大偏差补偿前9.4644-30.995340.4597第1次补偿后1.8828-11.611913.4947第2次补偿后4.3920-0.52564.9176
6结论

图10 两次误差补偿后光栅角度误差Fig.10 Grating angle errors after two-time error compensation
文中以一种大直径精密转台为研究对象,提出了一种基于激光追踪仪空间位置坐标信息检测的单自由度转台旋转角度的标定方法.该方法利用激光追踪仪可方便、快速检测被测点空间位置坐标的测量优势,具有操作简便、实施灵活的优点,大大简化了传统角度测量设备(如多面体棱镜等)的复杂安装与调整流程,并有效避免了人为因素对测量结果的干扰.该标定方法主要包括误差测量和误差补偿两方面,首先通过建立被测点空间位置坐标信息与转台角度之间的映射关系,并针对激光追踪仪测量精度的分析提出了被测点半径长度和测量角度间隔的选取原则,以充分利用激光追踪仪的位置测量精度实现转台转角误差的高精度测量;然后利用多项式插值方法获得转台转角误差随转角位形的变化规律,并将误差拟合补偿函数嵌入控制器中,采用修正光栅输出示数的方式来实现转角误差的实时补偿.
将该方法实施于一台安装有圆光栅的精密转台的标定实验中,可有效校正由圆光栅装配误差导致的角度定位误差,使其由标定前的40″降低至5″,充分验证了该方法的可行性和有效性.文中的研究思路和实验方法对指导其他同类设备的角度测量和角度补偿研究具有一定的参考价值.
参考文献:
[1]王明元,余海盛,杨连春,等.一种超低速转台速率指标的测量方法 [J].宇航计测技术,2013,33(4):21-23,38.
WANG Ming-yuan,YU Hai-sheng,YANG Lian-chun,et al.Measurement method of an ultra-low-speed turntable’s rate index [J].Journal of Astronautic Metrology and Measurement,2013,33(4):21-23,38.
[2]张光普,陈其林,陈宇华.液压等分回转台的设计应用[J].机械,2013(4):67-70.
ZHANG Guang-pu,CHEN Qi-lin,CHEN Yu-hua.The design and application of hydraulic direct rotary table [J].Machinery,2013(4):67-70.
[3]袁胜万,寸花英,李江艳,等.大型精密回转工作台传动性能分析研究 [J].组合机床与自动化加工技术,2014(3):37- 41.
YUAN Sheng-wan,CUN Hua-ying,LI Jiang-yan,et al.Large precision rotary table drive performance analysis and improvement [J].Modular Machine Tool & Automa-tic Manufacturing Technique,2014(3):37- 41.
[4]LUCIAN M,GHEORGHE S,CLAUDIU O,et al.High precision rotary table used on milling machining centres [J].Innovative Manufacturing Engineering,2013,371:121-125.
[5]高晓非,洪瑞,孟凡军,等.大型重载高精度转盘传动机构 [J].新技术新工艺,2014(6):7- 8.
GAO Xiao-fei,HONG Rui,MENG Fan-jun,et al.Large heavy high-precision turntable transmission mechanism [J].New Technology & New Process,2014(6):7- 8.
[6]王忠山,王毅,苏宝库.一种精密转台系统自适应摩擦补偿方法 [J].华南理工大学学报(自然科学版),2007,35(9):55-59.
WANG Zhong-shan,WANG Yi,SU Bao-ku.An adaptive friction compensation method for high-precision turntable system [J].Journal of South China University of Techno-logy(Natural Science Edition),2007,35(9):55-59.
[7]何俊,李文华.基于绝对式感应同步器的绝对角度测量系统 [J].仪表技术与传感器,2009(4):64- 66.
HE Jun,LI Wen-hua.Absolute angular system measurement system based on absolute inductosyn [J].Instrument Technique and Sensor,2009(4):64- 66.
[8]王帅,王显军,阴玉梅,等.一种便携式两轴转台角度测量系统的设计 [J].微计算机信息,2011(6):58- 60.
WANG Shuai,WANG Xiao-jun,YIN Yu-mei,et al.The design of an angle measurement system for a portable two-axis turntable [J].Microcomputer Information,2011(6):58- 60.
[9]倪国芬.一种高精度动态测角系统研究及实现 [J].航空精密制造技术,2013(2):18-20.
NI Guo-fen.Research and application in high precision dynamic angle measurement system [J].Aviation Precision Manufacturing Technology,2013(2):18-20.
[10]陈希军,任顺清.感应同步器测角误差的自动化检测与补偿 [J].电机与控制学报,2010(4):41- 45.
CHEN Xi-jun,REN Shun-qing.Automatic measurement and compensation of inductosyn angular displacement error [J].Electric Machines and Control,2010(4):41- 45.
[11]GRAETZ R J.On-axis self-calibration of angle measurement errors in precision rotary encoders [D].Vancouver:Department of Mechanical Engineering,University of British Columbia,2011.
[12]吉梅峰,蒋蓁,田志辉.基于光电码盘的三轴转台测角系统 [J].机电工程,2004,21(10):9-13.
JI Mei-feng,JIANG Zhen,TIAN Zhi-hui.The angle-mea-surement system of three-axis turntable based on photoelectric encoder [J].Mechanical & Electrical Enginee-ring Magazine,2004,21(10):9-13.
[13]GAO Hua,CHEN Hao,ZHANG Zhao-xiang,et al.Method of binocular rotation angle measurement based on machine vision [C]∥Proceedings of International Conference on Instrumentation & Measurement,Computer,Communication & Control.Harbin:IEEE,2014:462- 467.
[14]DONG Hong-xin,FU Qiang,ZHAO Xu,et al.Practical rotation angle measurement method by monocular vision [J].Applied Optics,2015,54(3):425- 435.
[15]CHEN Xi-jun,WANG Zhen-huan,WANG Zheng-bang,et al.Angle measurement error and compensation for pitched rotation of circular grating [J].Journal of Harbin Institute of Technology,2011,18(3):11-15.
[16]崔勇,徐岩.精密型转台角位移精度的测量方法研究 [J].计量与测试技术,2012,39(2):1-2.
CUI Yong,XU Yan.Research of angular displacement accuracy measuring method for precise turntable [J].Metrology & Measurement Technique,2012,39(2):1-2.
[17]雷经发,王德麾,袁中凡.基于机器视觉的平面夹角测量方法 [J].华南理工大学学报(自然科学版),2011,39(8):54-59.
LEI Jing-fa,WANG De-hui,YUAN Zhong-fan.A measurement method of plane angle based on machine vision [J].Journal of South China University of Technology(Natural Science Edition),2011,39(8):54-59.
[18]糜小涛,高胜英.圆光栅偏心对仿真转台角位置精度的影响 [J].长春理工大学学报(自然科学版),2014,37(3):9-12.
MI Xiao-tao,GAO Sheng-ying.Effect of eccentric of circular gratings on angular position accuracy of simulator [J].Journal of Changchun University of Science and Technology(Natural Science Edition),2014,37(3):9-12.
[19]唐松,方明,姚磊.安装偏心对圆光栅测角精度的影响及误差补偿技术研究 [J].计量与测试技术,2013(6):11-12,14.
TANG Song,FANG Ming,YAO Lei.Error compensation for installation eccentric of circular gratings [J].Metro-logy & Measurement Technique,2013(6):11-12,14.
[20]彭思,杨向东,吴聊,等.高精密型转台标定方法研究 [J].机械设计与制造,2012(4):1-3.
PENG Si,YANG Xiang-dong,WU Liao,et al.Calibration method research for high precision turntable [J].Machinery Design & Manufacture,2012(4):1-3.
[21]芦婷,程维明,孙麟治.精密定位工作台的定位精度标准分析对比 [J].机械设计与制造,2007(4):141-143.
LU Ting,CHENG Wei-ming,SUN Lin-zhi.The analysis and comparison of the position accuarcy on the precision positionging working table [J].Machinery Design & Manufacture,2007(4):141-143.
Angular Calibration Method of Precision Rotating
Platform Based on Laser Tracker
BAIPu-jun1XUENa1LIUSong-tao2SONGTao2LIJin-he1
(1. School of Mechanical Engineering, Tianjin University, Tianjin 300072, China;
2. Technical Department, Chenxing(Tianjin)Automation Equipment Co.Ltd., Tianjin 301701, China)
Abstract:For large-diameter precision rotating platforms, to adopt traditional methods to implement high-precision angular measurement is difficult. In order to solve this problem, a rotating angle measurement and compensation method for a single degree-of-freedom rotating platform is proposed on the basis of the spatial coordinates obtained by using a laser tracker. First, on the basis of the geometry theorem that a unique circle can be determined by any three non-collinear points, a mapping function between the rotating angle and the spatial coordinates is formulated. Through a comprehensive analysis of the relationship between the measurement error of the laser tracker and the angular error of the rotating platform, a criterion for the selection of measured radius and angle interval is made so as to fully utilize the measurement accuracy of the laser tracker to realize a high-precision measurement of the rotating angle error. Then, the polynomial interpolation method is utilized to obtain the change laws of the rotating angle error with the rotating angle position, and the real-time compensation of the rotating angle error is realized by embe-dding the fitted error mapping function into the control system and by modifying the output display of grating. Fina-lly, the proposed method is applied in a calibration experiment on a precision rotating platform equipped with circular gratings. The results show that the proposed method can effectively reduce the angular error caused by the assembly error of circular gratings, which decreases from 40″ to 5″.
Key words:precision rotating platform; grating measurement; calibration; laser tracker
doi:10.3969/j.issn.1000-565X.2016.01.015
中图分类号:TP216
作者简介:白普俊(1987-),男,博士生,主要从事工业机器人及其自动化系统研究.E-mail:baipujunaa@126.com†通信作者: 刘松涛(1987-),男,硕士,主要从事工业机器人机构设计及理论研究.E-mail:st2060@126.com
*基金项目:天津市人才引进与科技合作项目(13RCHZGX01118);天津市科技型中小企业技术创新项目(14C26211200362);国家自然科学基金面上项目(51475320)
收稿日期:2015- 04-24
文章编号:1000-565X(2016)01- 0100- 08
Foundation item: Supported by the General Program of the National Natural Science Foundation of China(51475320)

