基于十字型阵列的多频发射波束形成算法*
刘雪松 周凡 周泓 田翔 蒋荣欣 陈耀武
(浙江大学 数字技术及仪器研究所∥浙江省网络多媒体技术研究重点实验室, 浙江 杭州 310027)
基于十字型阵列的多频发射波束形成算法*
刘雪松周凡†周泓田翔蒋荣欣陈耀武
(浙江大学 数字技术及仪器研究所∥浙江省网络多媒体技术研究重点实验室, 浙江 杭州 310027)
摘要:针对平面接收阵阵元数量庞大导致的水下三维声学成像系统硬件开销和计算量过大的问题,提出了一种基于十字型阵列的三维声学成像的多频发射波束形成算法.该算法将发射波束方向划分为多个扇面,在每个扇面内依次向各波束方向发射不同频率的扇形波束信号,将发射次数从波束数减少到扇面数,从而缩短了扫描时间.仿真实验和计算量分析表明,文中算法能够获得与平面接收阵直接波束形成算法相同的波束性能,并且大幅降低了阵元数量和计算量.实际水下试验证明了该算法能够满足水下三维声学成像的实时性需求.
关键词:实时三维声学成像;多频发射;十字型阵列;波束形成;计算量需求
近年来,三维声学成像技术在水下探测及超声领域受到了广泛的关注,其发展对医疗图像、超声检测、水下机器人、海洋探测、海底施工以及沉积物打捞等应用均具有积极的意义[1- 4].相比于光学传感器,声学传感器具有获取观测场景三维信息的能力,同时受到水下浑浊度的影响很小.因此,实时三维声学成像系统在水下应用领域具有广泛的发展前景[5].
为获得场景三维信息,通常需要二维平面接收换能器阵列用于接收声学回波,构建三维图像[6].而平面接收阵的使用通常伴随着庞大的阵元数量,从而导致巨大的硬件开销和计算量[7].为了克服上述问题,Haupt[8]提出了一种基于遗传算法的阵列稀疏方法,可以在一定程度上减少阵元数量,降低系统复杂度.袁龙涛等[9]采用模拟退火算法实现了一种兼顾远场与近场的稀疏阵列优化方法,在保持系统性能的前提下大大降低了硬件成本.Palmese等[10]提出了一种Chirp Zeta 变换(CZT)波束形成算法,相比于直接波束形成算法,CZT波束形成算法的计算量降低了1~2个数量级.韩业强等[11]通过将整个平面接收阵划分为多个子阵,采用两级并行流水结构大大降低了波束形成算法的计算量,提高了计算效率.
另外,一些学者采用发射和接收阵列共同进行波束形成,通过降低阵列维度、以多个线阵代替平面接收阵列来实现阵元数量的减少.Karaman等[12]对一些不同形式的阵列配置进行了对比,这些阵列配置通过消除发射和接收阵列中冗余的阵元来简化阵列复杂度.Okino等[13]基于十字型阵列设计了一种三维海底地形测绘系统,采用两条相互垂直的线型阵列来实现三维声学图像的构建,极大地降低了系统的硬件开销.但十字型阵列在构建三维声学图像时,扫描观测场景所需的时间过长,导致其目前只能应用于一些近场或无实时性需求的环境中[14].
为了充分利用十字型阵列阵元数量少的优点,同时解决其实时性不足的问题,文中提出了一种基于十字型阵列的多频发射(MFT)波束形成算法,通过优化十字型阵列的发射过程来缩短其扫描时间,从而使其能够应用于水下实时三维声学成像.该算法将发射波束方向分割为多个扇面,在每个扇面内依次发射一系列不同频率的扇形波束信号,每个频率的信号均指向一个预设波束方向;在接收过程中,接收阵列在收到声纳回波后,通过离散傅里叶变换(DFT)抽取扇面内所有发射信号对应的频率信息,并在频域内并行地进行波束形成计算.最后通过仿真实验和实际水下试验分析该算法的性能.
1传统十字型阵列应用
十字型阵列是由两条相互垂直的线型阵列组成,如图1所示.接收阵列(1 mm×3 mm的条形阵元)和发射阵列(宽度2 mm、直径约30 mm的半圆环形阵元)的阵元数分别为M和N,阵元间距分别为dr和dt,以接收阵列和发射阵列交汇处作为坐标原点.

图1 十字型阵列结构Fig.1 Framework of the cross array
在传统十字型阵列应用中,发射阵列通过各阵元间的相移补偿,向预设的垂直波束方向发射一个扇形的窄带声纳波束信号,接收阵列接收来自该方向的声纳回波,并在该扇形波束范围内进行水平方向的波束形成.完成后,再向下一个垂直波束方向发射.当所有垂直波束方向发射完成后,即可形成一帧三维声学图像.在远场条件下,十字型发射阵列与接收阵列的波束方向图[15]可分别表示为
(1)
(2)
式中:BTr和BRe分别为发射和接收阵列的波束强度,它们分别是关于垂直和水平波束方向角βq、αp(1≤p≤P,1≤q≤Q)的函数,对应P×Q个波束方向;Sn(k)和Sm(k)分别为发射和接收阵元的声纳信号经过L点DFT运算的结果,k为DFT的线谱号,n(1≤n≤N)和m(1≤m≤M)分别为发射和接收阵元的索引号;θn、θm分别为发射和接收阵元的相位偏移参数,

(3)

(4)
f0为声纳信号的中心频率;c为声波在水下传播的速度,约为1 500m/s.十字型阵列整体的波束方向图为接收和发射波束方向图的乘积[1]:
(5)
其波束三维(3D)示意图如图2所示.
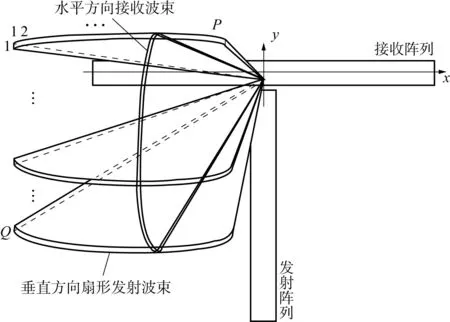
图2 十字型阵列的波束三维示意图Fig.2 3D schematic diagram of beams of the cross array
在十字型阵列的传统应用中,为了构建整个观测场景的三维声学图像,发射阵列需要向所有预设的垂直波束方向发射扇形波束信号,每次发射都需等待声纳回波从最远探测距离返回.因此,生成一帧三维声学图像所需时间正比于发射次数(垂直波束方向数Q)和最远探测距离(Rmax).如果要在50 m的范围生成54×54个波束,则构建一帧三维声学图像需要的时间为3.6 s(2RmaxQ/c).显然,传统十字型阵列应用无法满足水下实时三维声学成像的需求.
2多频发射波束形成算法
2.1 算法原理
为解决十字型阵列的实时性问题,文中提出了MFT波束形成算法,通过减少其发射次数来使其能够应用于实时水下三维声学成像.MFT波束形成算法的具体流程是:①将预设的垂直波束方向分割为K个扇面,在每个扇面内发射阵列依次向预设波束方向(共J个,Q=K×J)发射窄带扇形波束信号,每个方向对应一个不同的频率;②当该扇面内所有方向发射结束后,接收阵列收到声纳回波信号,并对回波信号进行DFT运算,同时计算回波中J个发射频率对应的结果,并行地在J个频域内进行波束形成,获得P×J个波束;③对余下扇面进行相同的操作,当所有扇面完成后,可以得到完整的P×Q个方向的波束结果.MFT算法的发射过程如图3所示.

图3 MFT波束形成算法的发射过程示意图Fig.3 Schematic diagram of transmitting process of MFT beamforming algorithm


图4 发射脉冲频率时域示意图Fig.4 Schematic diagram of frequency of transmitting pulses in time domain
因此,发射信号的时域表达式如下:
(6)
(7)
式中:垂直波束方向索引q是关于划分扇面序号kS和信号频率索引j的函数,
q(kS,j)=(kS-1)J+j
(8)
A为信号幅值;θn(fj,βq)为相位偏移参数,

(9)
相邻发射信号频率按照Δf 的步进频率递增,即
fj+1-fj=Δf
(10)

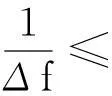
(11)
由式(6)-(9)可知,在MFT算法中,发射声纳信号及参数均是关于频率fj的函数.因此,发射阵列的波束方向图可表示为
(12)
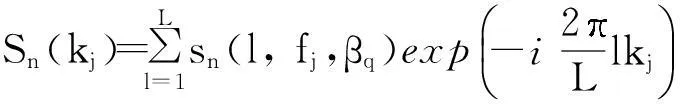
(13)
式中:Sn(kj)是采样信号sn(l,fj,βq)的L点DFT变换结果;kj为频率fj的线谱号,若采样频率为fs,则
(14)
接收阵列的波束方向图与式(2)相似,区别在于,在MFT算法中,接收阵列在J个频域上并行执行波束形成算法,其表达式如下:
(15)
(16)
式中:sm(l,fj,αp)是回波信号的采样数据;Sm(kj)是sm(l,fj,αp)的L点DFT变换结果;θm(fj,αp)是接收阵列的相位偏移参数,

(17)
由上述发射和接收波束形成过程可知,十字型阵列的波束方向角(αp,βq)有别于传统的平面接收阵列,是基于发射和接收阵列独立定义的,如图5所示.

图5 十字型阵列的方向角定义Fig.5 Definition of steering angles in the cross array
因此,MFT波束形成算法的十字型阵列关于波束方向角(αp,βq)的整体波束方向图如下:
(18)
式中,fj与βq的对应关系如式(8)所示.
MFT波束形成算法通过多频信号的顺序发射以及对回波信号的并行处理,有效地将十字型阵列的发射次数从垂直波束方向数Q减小到划分扇面数K,缩短了扫描时间.例如,在50 m的范围内生成54×54个波束,将垂直波束方向划分为6个扇面,相比于传统应用,构建一帧三维声学图像需要的时间从3.6 s(2RmaxQ/c)降低到0.4 s(2RmaxK/c),在水下三维成像应用中,已可以实现实时显示[5].
2.2 时延补偿

为构建三维图像,需要知道波束强度结果对应的三维空间坐标(x,y,z),其中(x,y)与波束方向角(αp,βq)存在对应关系,z代表距离信息,与声纳信号在水中的传播时间t的关系如下:
z=ct/2
(19)
而信号的时延反映到空间上则代表信号在水中传播的距离差.因此,时延可以转换成距离信息,补偿在对应的z值上.若以每个扇面中第一个频率的发射信号为参考,则各频率信号的时延值Γ可表示为

(20)
根据坐标中y得到对应的波束方向索引值q,并将式(8)代入式(20)中,则经过补偿得到的新的距离值z′为
(21)
若不进行时延补偿,在最终的三维声学图像中,笔直的物体将会显示为被分割成K(划分的扇面数)段的倾斜物体.采用MFT波束形成算法拍摄水下一条笔直的铁链,获得补偿时延和未补偿时延时的图像,如图6所示.

图6 时延补偿前后的笔直铁链图像Fig.6 Images of a straight iron chain before and after time delay compensation
2.3 计算量分析
为分析MFT波束形成算法的计算效率,就计算量与基于平面接收阵列的直接(DM)波束形成算法进行对比.
对于基于平面接收阵列的DM波束形成算法,首先需要计算M×N个通道的L点DFT结果,每个通道完成一次DFT运算需要2L次实数乘法、2(L-1)次实数加法,那么DFT运算所需要的实数计算量OP(DFT)为
OP(DFT)=[2L+2(L-1)]MN=
(4L-2)MN
(22)
其次,计算P×Q个波束的计算量,每个波束需要M×N次复数乘法及M×N-1次复数加法,则基于平面接收阵列的DM波束形成算法总的实数计算量OP(BF)可表示为
OP(BF)=OP(DFT)+(8MN-2)PQ=
(4L-2)MN+(8MN-2)PQ
(23)
对于MFT波束形成算法,N个通道的发射信号均通过预先计算存储在内存中,因此发射波束形成并无计算量需求.而在接收波束形成过程中,首先需要计算M个通道的L点DFT结果,然后计算P个波束,每个波束需要M次复数乘法和M-1次复数加法.此外,接收波束形成需要在J个频域上并行执行.因此,MFT波束形成算法总的实数计算量OC(BF)为
OC(BF)=[(4L-2)M+(8M-2)P]J=
[(4L-2)M+(8M-2)P]Q/K
(24)
为了比较基于平面接收阵列的DM波束形成算法和十字型阵列MFT波束形成算法的计算量,实验参数配置如下:DFT点数L=150,平面型阵列阵元数M×N=100×100,十字型阵列阵元数M+N=100+100,划分扇面数K=6.当波束方向数P×Q分别为50×50、100×100、150×150时,两种算法的计算量对比如表1所示.
表 1两种波束形成算法的计算量对比
Table 1Comparison of computational load between two beamforming algorithms

P×Q计算量基于平面接收阵列基于十字型阵列50×502.06×1088.31×105100×1008.06×1082.33×106150×1501.81×1094.49×106
由表1可以看出:在上述参数配置下,基于十字型阵列的MFT波束形成算法与基于平面接收阵列的DM波束形成算法相比,计算量可以降低接近3个数量级;当波束方向数增大时,十字型阵列的优势更加明显.因此,与基于平面接收阵列的DM波束形成算法相比,基于十字型阵列的MFT波束形成算法不仅减少了阵元数量,降低了系统复杂度,同时获得了较高的计算效率,并克服了十字型阵列的实时性问题.
3仿真实验及水下试验
3.1 仿真实验
为评估基于十字型阵列的MFT波束形成算法的性能,在Matlab环境下对其归一化波束方向图进行仿真实验,并与基于平面接收阵列的DM波束形成算法进行对比.
表2部分仿真参数设置
Table 2Configuration of some simulating parameters
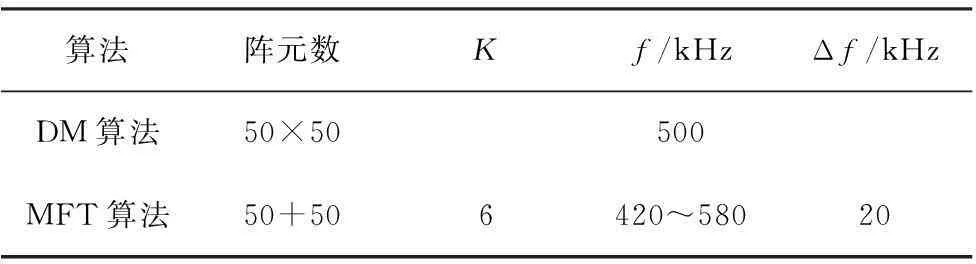
算法阵元数Kf/kHzΔf/kHzDM算法50×50500MFT算法50+506420~58020
在上述参数配置下,文中进行了两组仿真实验:第1组实验假设在(0°,0°)存在一个单点目标,信号中心频率为500 kHz,分别对基于平面接收阵列的DM波束形成算法和基于十字型阵列的MFT波束形成算法的波束方向图进行仿真,结果如图7所示.第2组实验选取MFT波束形成算法划分的第2个扇面,对该扇面中420 kHz和580 kHz信号(两个边界)对应的波束方向图进行仿真,结果如图8所示.
主瓣宽度和旁瓣峰值作为波束方向图的两个重要指标,主瓣宽度反映了三维声学成像的角度分辨率,其值越小,则成像角度分辨率越高,通常在归一化波束强度下降到-3 dB时测得;旁瓣峰值则体现了三维声学成像的目标识别能力,旁瓣峰值越低,则目标的识别精度越高,若旁瓣峰值过大,则可能会造成目标的误识别.
由图7可知,在相同的信号频率下,两种算法的主瓣宽度(1.12°)和旁瓣峰值(-15 dB)完全一致,并且能够获得相同的波束方向图.由此证明,十字型阵列能够在使用较少阵元的条件下获得和平面接收阵列相同的性能,降低系统硬件复杂度.
从图8可知,对于不同频率的信号,文中算法获得的主瓣宽度不同,420 kHz和580 kHz信号的主瓣宽度分别为0.97°和0.52°,频率越高,主瓣宽度越窄.因此,对于MFT波束形成算法,需要根据系统的角度分辨率需求,合理地选择每个扇面中发射信号的频率范围及步进频率.在本实验中,所有频率(420~580 kHz)对应的主瓣宽度均可满足系统的角度分辨率需求(1°),因此不同频率的发射信号不会对系统造成分辨率不均匀的影响.

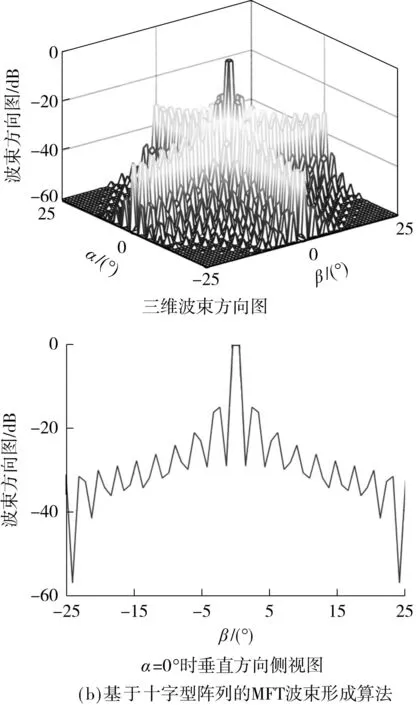
图7 两种波束形成算法的仿真结果Fig.7 Simulation results of two beamforming algorithms

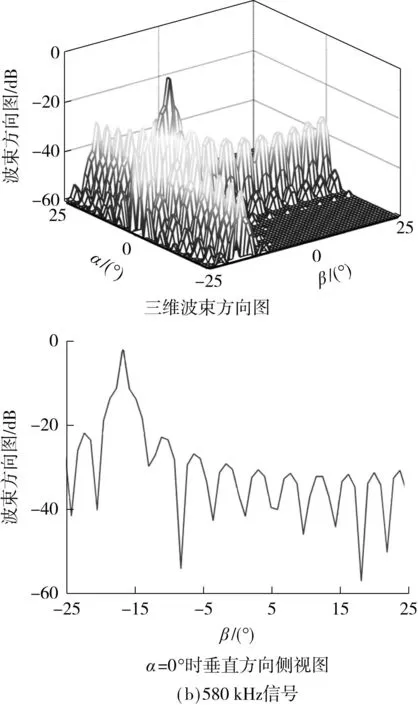
图 8 基于十字型阵列的MFT波束形成算法的仿真结果Fig.8 Simulation results of MFT beamforming algorithm based on cross array
在MFT波束形成算法中,对于不同位置的目标,其旁瓣峰值(500 kHz对应-15 dB,420 kHz对应-16.7 dB,580 kHz对应-22.9 dB)均小于基于平面接收阵列的DM波束形成算法(-15 dB).由此可知,基于十字型阵列的MFT波束形成算法的目标识别能力不低于基于平面接收阵列的DM波束形成算法.在实际三维成像过程中,通过设置波束强度阈值滤除结果中低于旁瓣峰值的波束信号,则可以确保不会造成目标的误识别.
此外,在采用MFT波束形成算法时,还需综合考虑两个因素:系统帧率及计算量.该算法所能获得的帧率与扇面数K成反比(帧率=c/(2RmaxK)),而由式(24)可知,算法计算量也与K成反比.因此,在提高帧率的同时,必然会增加系统计算量.通过多组仿真实验发现,合理的扇面数K为3~6,在大幅降低计算量的同时,也可获得满足水下三维成像实时性需求的帧率.
综上所述,MFT波束形成算法解决了十字型阵列实时性不足的问题,相比于基于平面接收阵列的DM波束形成算法,基于十字型阵列的MFT波束形成算法降低了系统的硬件复杂度和计算量,同时能够获得与平面接收阵列相近的性能,并且在观测场景内均可准确地识别目标.
3.2 水下试验
基于MFT波束形成算法,文中设计并实现了一台采用十字型阵列的原理样机,并进行了实际湖试试验.拍摄目标为一个立方体铁框,放置在水中,距样机约8 m处.图9展示了拍摄的3D图像效果,可以看到,作为目标的立方体铁框出现在显示屏中央.
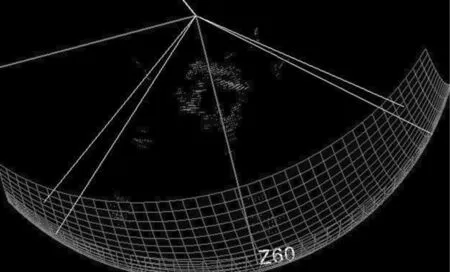
图9 立方体铁框的3D图像Fig.9 3D image of an iron cube
实际水下试验进一步证明了MFT波束形成算法的有效性.基于MFT波束形成算法,使用十字型阵列设计并实现了低硬件复杂度的原理样机,获得的水下三维成像结果表明,观测人员能够以任意角度观察场景中的目标,同时在50 m的距离内获得了最少每秒2帧的帧率,满足水下三维声学图像的实时处理及显示.
4结论
针对三维声学成像中平面接收阵列阵元数量巨大而导致的硬件开销大和计算量需求高的问题,文中提出了基于十字型阵列的多频发射波束形成算法,以降低系统硬件复杂度和计算量,解决十字型阵列的实时性问题.然而,由于系统需要采用宽带阵列,故增加了一定的成本.但与其在降低系统复杂度相比,上述问题则是可以接受的.仿真实验和计算量分析结果表明,与基于平面接收阵列的DM波束形成算法相比,基于十字型阵列的MFT波束形成算法能够将阵元数量从M×N减小到M+N,并且保持波束方向图中主瓣宽度和旁瓣峰值等性能指标不变,在任意波束方向上均可正确地识别目标,同时计算量降低近3个数量级.实际的水下试验证明了基于十字型阵列的MFT波束形成算法的三维声学成像系统能够有效地拍摄实时水下三维图像.
参考文献:
[1]MURINO V,TRUCCO A.Three-dimensional image gene-ration and processing in underwater acoustic vision [J].Proceedings of the IEEE,2000,88(12):1903-1948.
[2]NEGAHD Aripour S,MADJIDI H.Stereovision imaging on submersible platforms for 3-D mapping of benthic habitats and sea-floor structures [J].IEEE Journal of Oceanic Engineering,2003,28(4):625-650.
[3]PALMESE M,TRUCCO A.From 3-D sonar images to augmented reality models for objects buried on the seafloor [J].IEEE Transactions on Instrumentation and Measurement,2008,57(4):820-828.
[4]WACHOWSKI N,AZIMI-SADJADI M R.A new synthetic aperture sonar processing method using coherence analysis [J].IEEE Journal of Oceanic Engineering,2011,36(4):665- 678.
[5]TRUCCO A,PALMESE M,REPETTO S.Devising an affordable sonar system for underwater 3-D vision [J].IEEE Transactions on Instrumentation and Measurement,2008,57(10):2348-2354.
[6]TRUCCO A.Thinning and weighting of large planar arrays by simulated annealing [J].IEEE Transactions on Ultrasonics,Ferroelectrics and Frequency Control,1999,46(2):347-355.
[7]PALMESE M,TRUCCO A.An efficient digital CZT beamforming design for near-field 3-D sonar imaging [J].IEEE Journal of Oceanic Engineering,2010,35(3):584-594.
[8]HAUPT R L.Thinned arrays using genetic algorithms [J].IEEE Transactions on Antennas and Propagation,1994,42(7):993-999.
[9]袁龙涛,周凡,陈耀武.相控阵三维摄像声纳系统的稀疏阵列优化设计 [J].华南理工大学学报(自然科学版),2013,41(1):29-37.
YUAN Long-tao,ZHOU Fan,CHEN Yao-wu.Optimization design of sparse arrays for phased-array 3D imaging sonar systems [J].Journal of South China University of Technology(Natural Science Edition),2013,41(1):29-37.
[10]PALMESE M,TRUCCO A.Three-dimensional acoustic imaging by chirp zeta transform digital beamforming [J].IEEE Transactions on Instrumentation and Mea-surement,2009,58(7):2080-2086.
[11]韩业强,田翔,陈耀武.采用分布式并行子阵波束形成的水下三维成像 [J].浙江大学学报(工学版),2014,48(2):368-376.
HAN Ye-qiang,TIAN Xiang,CHEN Yao-wu.Underwater 3D imaging by distributed and parallel subarray beamforming algorithm [J].Journal of Zhejiang University(Engineering Science),2014,48(2):368-376.
[12]KARAMAN M,WYGANT I O,KHURI-YAKOB B T.Minimally redundant 2-D array designs for 3-D medical ultrasound imaging [J].IEEE Transactions on Medical Imaging,2009,28(7):1051-1061.
[13]OKINO M,HIGASHI Y.Measurement of seabed topography by multibeam sonar using CFFT [J].IEEE Journal of Oceanic Engineering,1986,11(4):474- 479.
[14]AHMAD F,FRAZER G J,KASSAM A,et al.Design and implementation of near-field,wideband synthetic aperture beamformers [J].IEEE Transactions on Aerospace and Electronic Systems,2004,40(1):206-220.
[15]NIELSEN R O.Sonar signal processing [M].Boston:Artech House,1991.
Multi-Frequency Transmitting Beamforming Algorithm
Based on Cross Array
LIUXue-songZHOUFanZHOUHongTIANXiangJIANGRong-xinCHENYao-wu
(Institute of Advanced Digital Technology and Instrumentation∥ Zhejiang Provincial Key Laboratory for Network Multimedia
Technologies, Hangzhou 310027, Zhejiang, China)
Abstract:In order to solve the problems of the huge hardware cost and computational load in underwater 3D acoustic imaging system, which is caused by the large number of elements in a receiving planar array, a multi-frequency transmitting beamforming algorithm is proposed for the real-time 3D acoustic imaging on the basis of cross array. In the algorithm, first, transmitting steering directions are subdivided into several sectors. In each sector, a series of fan-shaped beams with different frequencies are transmitted sequentially, and each beam is steered to a specific direction. Then, the number of transmissions is reduced from the number of beams to the number of sectors, thus shortening the scanning time. Simulation results and the analysis of computational load show that the proposed algorithm can obtain the same performance as the direct beamforming method on the basis of the receiving planar array and dramatically reduce both the transducer number and the computational load. Real underwater experiments de-monstrate that the proposed algorithm can meet the real-time requirement in underwater 3D acoustic imaging applications.
Key words:real-time 3D acoustic imaging; multi-frequency transmitting; cross array; beamforming; computational requirement
doi:10.3969/j.issn.1000-565X.2016.01.004
中图分类号:TB56
作者简介:刘雪松(1988-),男,博士,主要从事嵌入式系统、声纳信号处理研究.E-mail:11015006@zju.edu.cn†通信作者: 周凡(1978-),男,副教授,主要从事嵌入式系统、声纳信号处理、FPGA并行计算研究.E-mail:fanzhou@mail.bme.zju.edu.cn
*基金项目:国家自然科学基金面上项目(41276090);国家“863”计划项目(2014AA091301);浙江大学中央高校基本科研业务费专项资金资助项目
收稿日期:2015-04-21
Foundation items: Supported by the General Program of the National Natural Science Foundation of China(41276090) and the National High-Tech R & D Program of China(2014AA091301)

