基于线纹尺的线结构光视觉传感器标定新方法*
邝泳聪 崔亮纯
(华南理工大学 机械与汽车工程学院, 广东 广州 510640)
基于线纹尺的线结构光视觉传感器标定新方法*
邝泳聪崔亮纯
(华南理工大学 机械与汽车工程学院, 广东 广州 510640)
摘要:为了实现传感器简单、快速、高精度的标定,提出了一种基于线纹尺的线结构光视觉传感器直接标定新方法,设计了平面靶标与特征点提取算法.即通过获取已知三维空间坐标特征点的图像坐标,直接建立亚像素物像索引表,实现了系统的直接标定.标定实验与测量实验结果表明:文中标定新方法操作简单,易于实现,具有较高的标定精度,Z轴、X轴方向的测量误差均值分别为0.004 5 mm 和0.013 0 mm,能够满足工业生产与测量的基本需求.
关键词:线结构光;视觉传感器;标定;特征点提取;三维测量
当今社会,随着计算机技术与图像处理技术的不断突破与完善,非接触式三维测量技术被广泛应用于三维重建、工业测量、质量控制等领域.非接触式三维测量的方法有很多,包括:激光三角法、双目视觉法、全息干涉法、相位法等.其中,激光三角法是一种发展较早的非接触三维测量技术,由于其具有速度快、精度高、抗干扰能力强、结构简单、维护方便等特点而备受国内外学者关注[1-5].目前,德国、日本、美国等国的几十家高新技术企业已形成了较为完善的产业规模,例如:日本 KEYENCE公司推出的形状轮廓测量显微系统VR-3000系列,可实现全自动超高速高精度的三维轮廓测量,测量精度可达0.002 mm;德国 GOM 公司推出的机载式三维扫描仪ATOS Compact Scan,可安装于机器臂上,构成流动式三维测量机,测量精度可达0.005~0.030 mm.然而,虽然国外厂商的产品在精度、速度、易操作性等方面都达到了较高的水平,但总的来说存在价格昂贵、产品通用性差等问题,制约着激光三角法测量技术在国内的推广与应用.随着我国工业的发展,激光三角法测量技术的应用范围仍在不断扩大,现代工业生产与测量对低成本、高精度、易操作的线结构光视觉传感器的需求也越来越大[6-8].
目前,线结构光视觉传感器的标定方法主要分为两类:传统标定方法和直接标定方法.传统标定方法在标定过程中需基于理想针孔模型与镜头畸变模型建立几何成像数学模型,然后分步标定模型中的未知参数值,再标定光平面与摄像机的位置关系,如:Xu等[9]先建立通用匹配的高一致性高度差模型,然后使用平面标定板来进行模型参数的标定.Dhillon等[10]基于针孔成像原理与交比不变性建立几何投影成像模型并进行模型参数的初标定,然后通过基于三次样条曲线的方法对模型参数进行优化.此外,较为著名的模型还有直接线性变换模型(DLT)[11]、TSAI模型[12]、WENG模型[13]等.这些几何成像数学模型在实际运用中会忽略摄像机、镜头、线结构光中其他非线性畸变因素,导致其标定精度较低.因此,近年来,国内外学者提出了直接标定方法,直接标定方法不需要建立几何成像数学模型,如:熊会元等[14]使用精加工锯齿形标定块,以激光线与标定块各棱线的交点为标定点,利用基于二元五次多项式拟合的标定模型实现直接标定.邹媛媛等[15]使用高精度组合量块与三维精密位移平台,通过建立已知三维空间坐标点与相应图像坐标的对应关系,实现直接标定.Liu等[16]使用标准球型标定块,通过获取线结构光在标定块上的投影图像,求出球体边缘轮廓与投影轮廓的交点来作为光平面上的标定点,然后通过基于最大似然准则的非线性优化算法直接求出光平面空间方程的最优解.
文中在基于现有直接标定算法的研究基础上,提出了一种基于线纹尺的线结构光视觉传感器直接标定新方法,设计了平面靶标与特征点提取算法,通过获取已知三维空间坐标特征点的图像坐标,直接建立亚像素物像索引表,实现系统的直接标定.
1基于线纹尺的直接标定法
1.1 直接标定法原理
线结构光视觉传感器主要是基于激光三角法测量原理设计的,如图1所示.

图1 激光三角法测量原理Fig.1 Measurement principle of laser triangulation
根据激光光轴与摄像机光轴之间的夹角θ,以及激光在摄像机像平面上成像的位置变化Δh,通过式(1)可获得被测物体表面的高度变化ΔH[17]:
(1)
式中,l为激光光轴与摄像机光轴交点到镜头透镜的距离,D为镜头透镜到摄像机像平面的距离.
从式(1)可知,激光三角法对激光器、摄像机与被测物体表面之间的位置参数比较敏感,在测量过程中测量系统任意一个参数的变化都会直接影响测量结果.因此,线结构光视觉传感器的标定是激光三角法测量中非常关键的一步.
传统标定方法的实质是,基于理想针孔模型与镜头畸变模型建立几何成像数学模型,然后分步标定模型中的未知参数值,进而确定从三维空间点到图像特征点的拓扑关系.因此,在实际运用中会忽略摄像机、镜头、线结构光中其他非线性畸变因素,导致其标定精度较低.但直接标定法不需要建立几何成像数学模型,不需要标定摄像机内外参数与光平面的相关参数,而是通过获取已知三维空间坐标特征点的图像坐标,直接建立图像坐标与三维空间坐标之间的对应关系,实现系统的直接标定,标定原理如图2所示.

图2 直接标定方法原理Fig.2 Principle of direct calibration
在图2中,已知线结构光光平面上特征点a1、a2、b1、b2的三维空间坐标(X,Y,Z),通过获取像平面上对应点a1′、a2′、b1′、b2′的图像坐标(U,V),即可直接建立图像坐标与三维空间坐标之间的对应关系.其中,线结构光光平面在三维空间坐标系的O-XZ平面上,则图像坐标系U轴对应三维空间坐标系X轴,图像坐标系V轴对应三维空间坐标系Z轴.然后在O-UV图像坐标系中,通过插值运算对区域a1′a2′b1′b2′内的各像素点赋予缺失的三维坐标值,即可建立完整的物像索引表I.在实际测量使用中,将被测物体表面放置在工作区域a1a2b1b2内,根据传感器对特征点获取得到的图像坐标,直接在物像索引表I中查找相应的图像坐标,即可得到相应的三维空间坐标,完成三维测量.
此外,根据不同的标定精度要求,可以在光平面特征点a1与a2、b1与b2之间增加多个特征点,分别标记为a1-an、b1-bn,则可在O-UV图像坐标中得到对应的点为a1′-an′、b1′-bn′.随着a1与a2、b1与b2之间特征点密度的增加,O-XZ平面X轴方向的标定精度也会越好,但标定过程中的计算量会增加,标定成本也会越高.同理,在a1-an所在平面与b1-bn所在平面之间增加多个不同高度的标定面,增加相应的特征点c1-cn,d1-dn,…,z1-zn,也会提高O-XZ平面Z轴方向的标定精度.考虑到标定精度的要求以及标定成本的控制,文中在标定方法的设计上,选择以1 mm的点间距将a1a2划分为n 个特征点,以0.05 mm的高度间距设置m 个标定面,共设置n×m 个特征点.
1.2 平面靶标设计及特征点提取
为了在各个标定面上以1 mm的点间距设置n 个特征点,设计了如图3所示的平面靶标.平面靶标主要由中间一系列的平行线组成,相邻平行线之间的间距为1 mm.靶标左右两端分布有一组对齐刻线,用于调整线结构光,以保证线结构光与平面靶标上的平行线垂直.进行标定时,将线结构光投射到平面靶标上产生一条光条,光条与平行线相交形成一组交点.由于平行线之间的间距为1 mm,则所得交点的点间距也为1 mm,因此交点即可作为标定所需的特征点.在实际使用中,以图3的平面靶标为基础,通过玻璃光刻技术制作成一高精度的玻璃线纹尺.通过光刻技术制作的线纹尺,具有平面度好、精度高等优点,100 mm量程的刻线位置偏差均在0.001 mm以内,能满足标定精度的要求.

图3 平面靶标Fig.3 Planar target
为了准确获取特征点在图像坐标系下的坐标(U,V),并确定对应的三维空间坐标(X,0,0),其过程主要包括以下几个步骤.
(1)光条中心提取.保持线纹尺固定,开启与关闭线结构光,分别获取有光条投射与无光条投射的两幅靶标图像,如图4(a)、4(b)所示.将两幅靶标图像进行灰度相减,即可提取光条的投射区域,如图4(c)所示.由于光条沿图像坐标系U轴行方向分布,光条宽度在12 个像素以内,因此用11×1的滑窗沿图像坐标系V轴列方向搜索.进行第j列搜索时,当滑窗内像素点的灰度和Sum(j)最大且Sum(j)>T时,取此时滑窗中心点作为该列的粗略光条中心点Mj,其中T是根据实际经验得出的灰度和阀值(这里T=200).最后,采用灰度重心法[18]在V轴列方向⎣Mj-3,Mj+3」区间内精确提取第j列光条中心的亚像素V轴坐标Cj:
(2)

图4 特征点提取Fig.4 Extraction of feature points
(2)特征点图像坐标提取.如图4(a)、4(b)所示,由于两幅图像的区别在于是否有光条投射,因此当光条中心V轴坐标点集ΩC已知时,在图4(b)上用1×6的滑窗沿点集ΩC从左往右逐列搜索,计算滑窗内像素点的灰度和分布曲线,提取灰度和分布曲线中的灰度和波谷,即为黑色平行线与光条交点的U轴坐标.为了提高交点图像坐标提取的精度与鲁棒性,在提取过程中,首先对图4(b)采用3×3方形模块进行平滑处理,然后通过式(3)对图像灰度值进行拉伸,再进行灰度和波谷的搜索:

(3)
对提取出来的灰度和波谷点再次按照步骤(1)中的灰度重心法,即可提取更为精确的交点U轴坐标.结合步骤(1)得到的光条中心V轴坐标点集ΩC,即可得到特征点点集ΩP的图像坐标值(U,V),提取结果如图4(d)所示.
(3)确定特征点三维空间坐标.以平面靶标在视场范围内左边第1条平行线为0刻度线,则第1条平行线与光条交点对应的三维空间X轴坐标为0,依次往右,各交点对应的三维空间X轴坐标可由式(4)求出:
xn=(n-1)d
(4)
式中,d=1mm,n=1,2,…,n,n为特征点点集ΩP的元素个数.
1.3 标定过程
由于结构光光平面在三维空间坐标系的O-XZ平面上,图像坐标系U轴对应三维空间坐标系X轴,图像坐标系V轴对应三维空间坐标系Z轴,为了在图像坐标系上建立物像索引表,需要依次获取三维空间坐标系的O-XZ平面上光平面内已知三维空间坐标特征点的图像坐标,以实现直接标定.其标定过程具体步骤如下:
1)在单自由度精密位移平台的运动轴Z轴上安装线结构光视觉传感器,将基于平面靶标制作而成的线纹尺固定在一块精加工的铝板上,将铝板放置在精密位移平台的工作台上.开启线结构光视觉传感器,将线结构光投射到线纹尺上产生一条光条,调整铝板的位置使得光条在线纹尺左右两端的对齐刻线上的读数一致,保证光条垂直于线纹尺上的平行线.
2)操作单自由度精密位移平台与线结构光视觉传感器,采集三维空间坐标系O-XZ平面上光平面内不同高度的靶标图像,其操作过程如下:
(1)调整单自由度精密位移平台Z轴的初始位置,使得光条在图像坐标系上落在物像索引表的起始位置,并以此时Z轴的位置作为0基准面.
(2)操作单自由度精密位移平台以0.05 mm的步进距离改变Z轴的位置,并在同一Z轴位置上,分别获取有光条投射与无光条投射的两幅靶标图像.
3)对步骤2)采集的一系列靶标图像进行特征点提取,得到各个Z轴位置上特征点的图像坐标值(U,V)与三维空间X轴坐标,并根据步骤2)中Z轴的运动记录,得到特征点相应的三维空间Z轴坐标.
4)建立一个二维数组I,根据步骤3)确立的图像坐标值(U,V)与三维空间坐标值(U,V)之间的对应关系,以特征点的图像坐标值(U,V)作为行列数,在二维数组I相应位置赋予相应的三维空间坐标值(X,Z).由于相邻平行线之间的间距与Z轴步进距离的限制,二维数组I中相邻特征点元素之间存在无赋值的元素,因此,最后通过基于三角形的三次插值法对二维数组I进行插值运算.
至此,即可完成亚像素物像索引表的建立,实现线结构光视觉传感器的直接标定.
2实验验证与结果分析
为验证文中提出的标定新方法的有效性,采用自主研发的线结构光视觉传感器搭建实验平台,进行线结构光视觉传感器的标定实验与精度验证实验,如图5所示.本实验平台使用的线结构光视觉传感器采用HITACHI KP-FMR200WCL型相机、深圳市视清科技有限公司DTCA230-37C型双侧远心镜头和波长为410 nm的线结构光发生器.其中,相机分辨率为2 048 像素×1 088像素.此外,本实验平台使用的单自由度精密位移平台可在Z轴方向平移,其分辨率为0.000 5 mm.
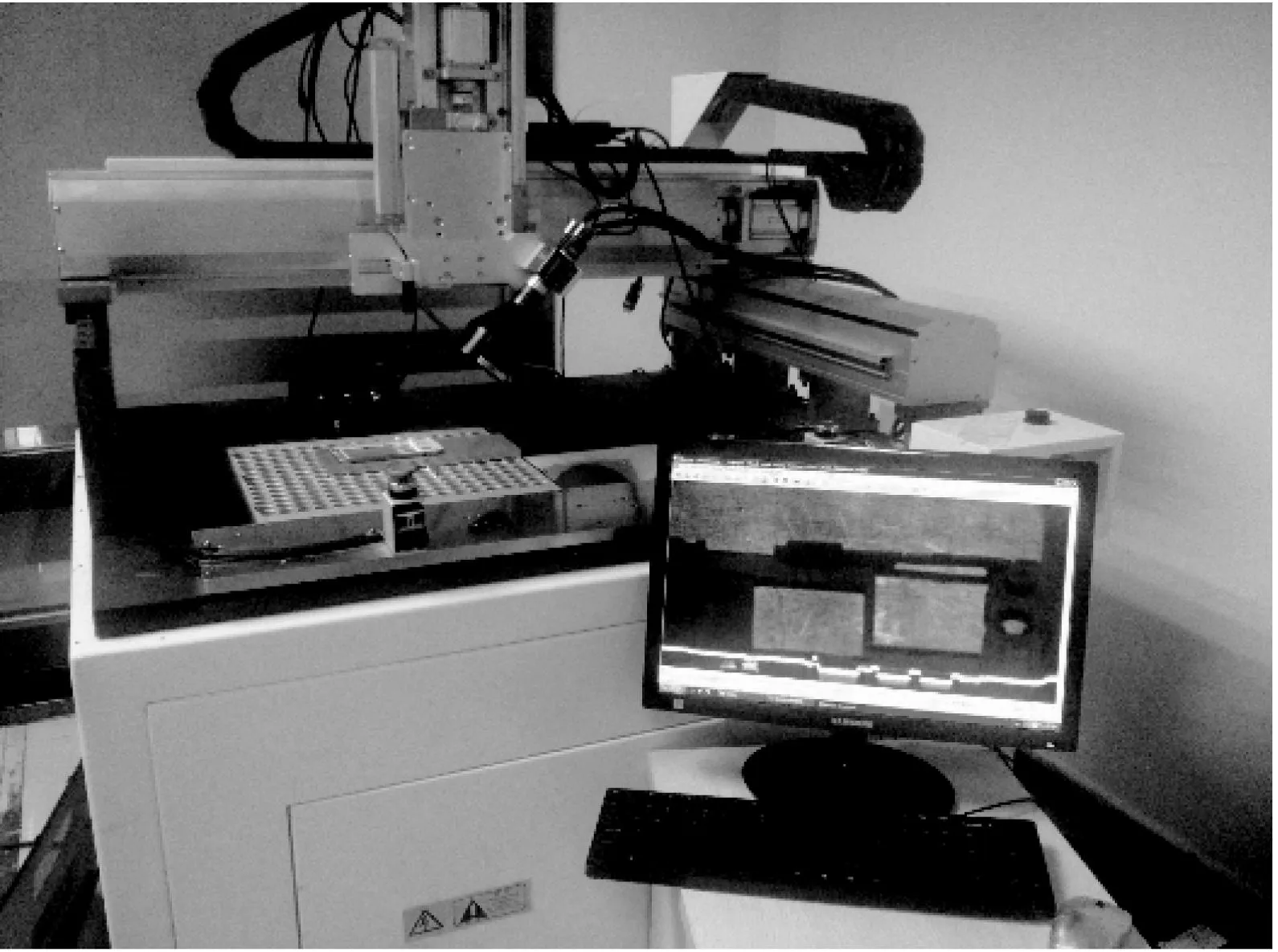
图5 实验平台Fig.5 Experiment platform
实验流程如下:
(1)根据文中提出的标定方法,以平面靶标为基础,通过玻璃光刻技术制作一高精度的玻璃线纹尺,然后对线结构光视觉传感器进行直接标定,建立亚像素物像索引表.在本次标定实验中,标定的Z轴高度为5 mm,标定的X轴宽度为74 mm.
(2)对线结构光视觉传感器进行Z轴测量精度的实验分析:将线结构光视觉传感器已标定的工作区域分成8个区域,如图6所示.在各区域内,依次将不同高度的标准2级量块放置于工作台上,以量块中心平面与工作台之间的高度差作为测量高度,重复测量多次,部分实验结果如表1、图7所示.其中,由于量块采用高反光材料,在实验过程中会在工作区域的中间区域产生较大的光斑,影响测量的结果,因此在本次实验中避开了中间区域.
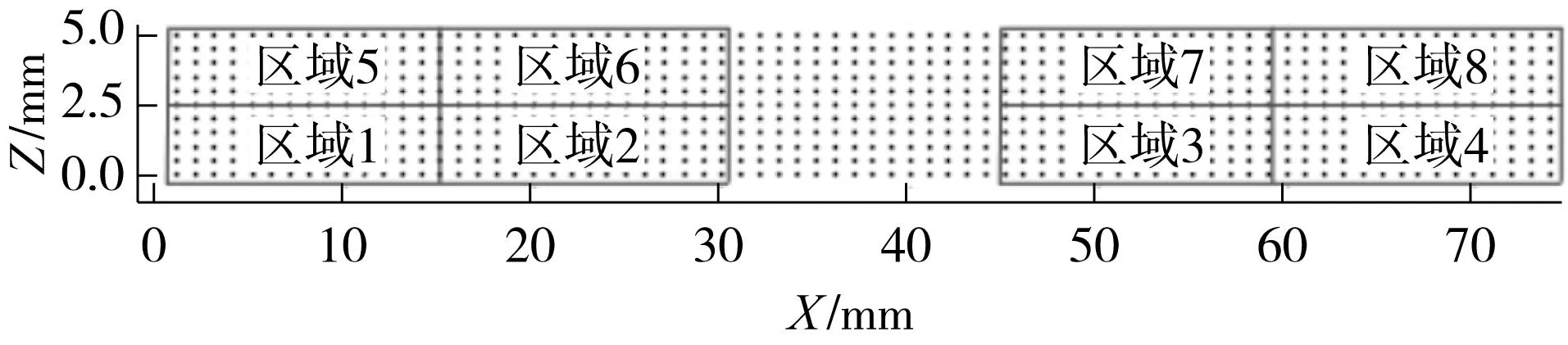
图6 区域划分Fig.6 The division of region
表1Z轴测量数据1)

Table1 Measurement data in Z axis
1)量块高度为1.000 0 mm.

图7 Z轴测量误差分布直方图Fig.7 Measurement error distribution histogram in Z axis
(3)对线结构光视觉传感器进行X轴测量精度的实验分析:在线结构光视觉传感器已标定的工作区域内,将线纹尺放置于工作台上,提取光条与平行线的交点作为实验测量点,重复测量多次,部分实验结果如表2、图8所示.
Z轴的最大绝对误差、最小绝对误差、绝对误差均值和标准偏差分别为0.017 6、0.000 1、0.004 5、0.003 6 mm,X轴的依次为0.043 0、0.001 3、0.013 0、0.009 0 mm.
从表1、图7可知,Z轴方向同一高度的量块测量值略有波动,经初步分析得,测量误差来源于精度验证实验中,是因为被测量块与工作台之间存在贴合间隙.从表2、图8及X轴、Z轴的测量误差统计数据可知,X轴方向的测量误差值较大,且有较大波动,经初步分析得知,该测量误差来源于标定实验中,是因为线纹尺的刻线有一定的宽度,对特征点的精确提取存在一定影响.
为了对比文中标定新方法与现有直接标定方法之间的差异,分别将文献[14]、 [15]与文中标定新方法的相应实验数据列于表3中.从表3中可知,文中标定新方法在测量精度上优于文献[14]、 [15]中提出的直接标定法,在特征点的获取上也更为简单、快速.
综合以上实验结果可知,采用文中提出的直接标定新方法标定的线结构光视觉传感器在Z轴、X轴方向上均具有较高的测量精度,Z轴方向的测量误差均值为0.004 5 mm,X轴方向的测量误差均值为0.013 0 mm,初步验证了标定方法的有效性.
表2X轴测量数据

Table 2 Measurement data in X axis
1)L表示理论值.
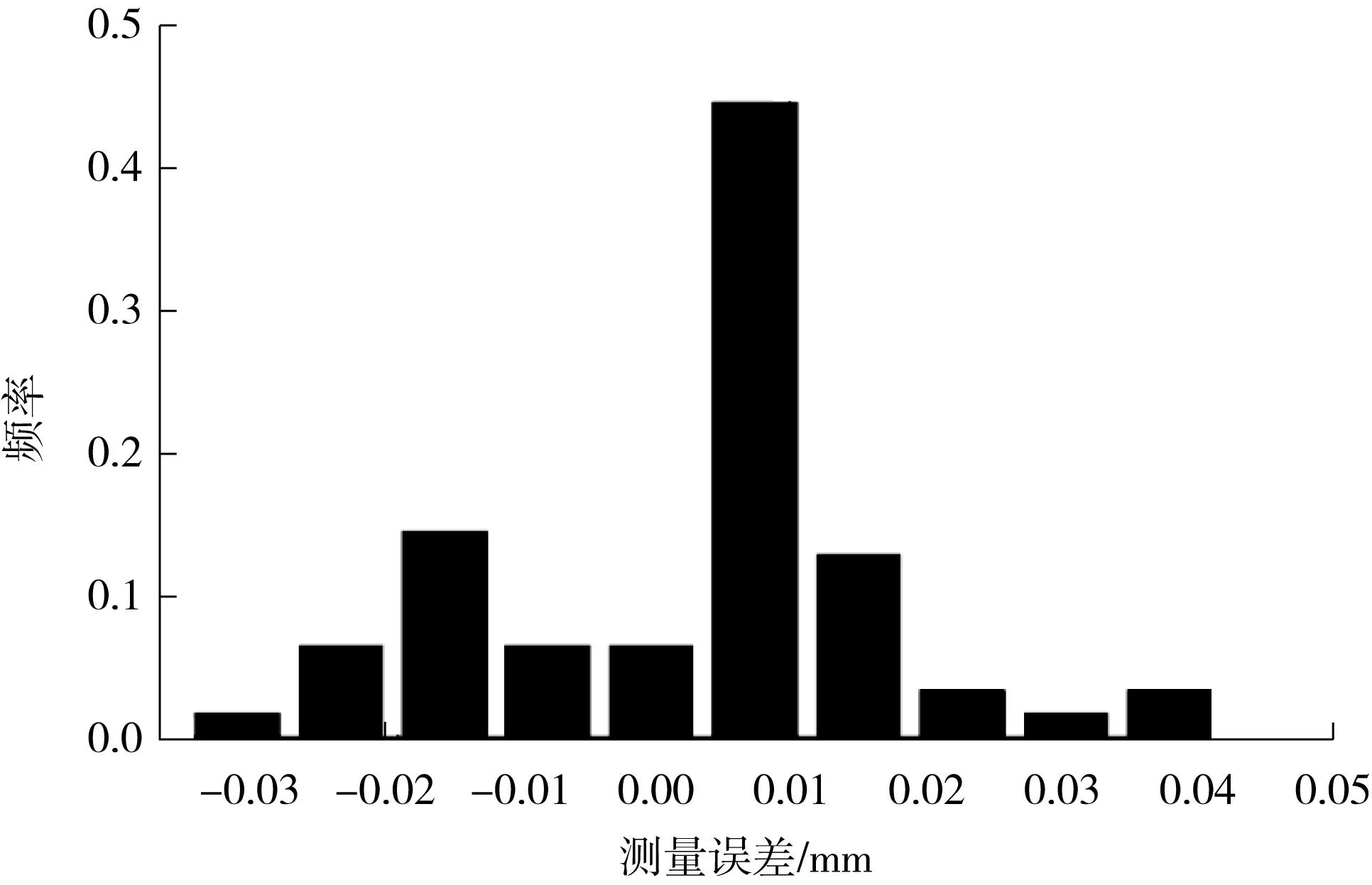
图8 X轴测量误差分布直方图Fig.8 Measurement error distribution histogram in X axis
表3不同标定方法的性能
Table 3Performance of different calibration methods

标定方法绝对误差均值/mmZ轴方向X轴方向单次采集特征点个数文献[14]的方法0.03400.034015文献[15]的方法0.02790.023710文中标定新方法0.00450.013074
3结语
文中提出了一种基于线纹尺的线结构光视觉传感器直接标定新方法,设计了平面靶标与特征点提取算法,采用自主研发的线结构光视觉传感器搭建实验平台,进行线结构光视觉传感器的标定实验与精度验证实验.其中,笔者自主研发的线结构光视觉传感器不仅研发与标定成本远低于国外厂商的集成式线结构光视觉传感器,而且可根据使用要求搭配不同的硬件配置.实验结果表明:文中标定新方法标定精度高,易于操作和实现,Z轴方向的测量误差均值为0.004 5 mm,X轴方向的测量误差均值为0.013 0 mm,能够满足工业生产与测量的基本需求.
参考文献:
[1]袁夏.三维激光扫描点云数据处理及应用技术 [D].南京:南京理工大学,2006.
[2]汤强晋.激光三角法在物体三维轮廓测量中的应用 [D].南京:东南大学,2006.
[3]曾祥军,霍金城,吴庆阳.线结构光三维测量系统扫描方向的标定 [J].中国激光,2012,39(1):0108002/1-5.
ZENG Xiang-jun,HUO Jin-cheng,WU Qing-yang.Calibration method for scanning direction of 3D measurement system based on linear-structure light [J].Chinese Journal of Lasers,2012,39(1):0108002/1-5.
[4]CIGADA A,MANCOSU F,MANZONI S,et al.Laser-triangulation device for in-line measurement of road texture at medium and high speed [J].Mechanical Systems and Signal Processing,2010,24(7):2225-2234.
[5]袁振宇.基于线结构光扫描的脚型重构测量研究 [D].合肥:安徽大学,2014.
[6]陈会,密保秀,高志强.基于畸变规律的三维结构光测量系统标定 [J].光学学报,2013,33(12):215002/1-9.
CHEN Hui,MI Bao-xiu,GAO Zhi-qiang.Calibration of 3D structured light measurement system based on the properties of lens distortion [J].Acta Optica Sinica,2013,33(12):215002/1-9.
[7]王鹏.线结构光三维自动扫描系统关键技术的研究 [D].天津:天津大学,2008.
[8]LILIENBLUM E,AL-HAMADI A.A structured light approach for 3-D surface reconstruction with a stereo line-scan system [J].IEEE Transactions on Instrumentation and Measurement,2015,64(5):1266-1274.
[9]XU J,DOUET J,ZHAO J G,et al.A simple calibration method for structured light-based 3D profile measurement [J].Optics and Laser Technology,2013,48:187-193.
[10]DHILLON D S,GOVINDU V M.Geometric and radiometric estimation in a structured-light 3D scanner [J].Machine Vision and Applications,2015,26(2):339-352.
[11]CHEN L,ARMSTRONG C W,RAFTOPOULOS D D.An investigation on the accuracy of three-dimensional space reconstruction using the direct linear transformation technique [J].Journal of Biomechanics,1994,27(4):493-500.
[12] TSAI R Y.A versatile camera calibration technique for high-accuracy 3D machine vision metrology using off-the-shelf TV cameras and lenses [J].IEEE Journal of Robotics and Automation,1987,3(4):323-344.
[13]WENG J,COHEN P,HERNIOU M.Camera calibration with distortion models and accuracy evaluation [J].IEEE Transactions on Pattern Analysis and Machine Intelligence,1992,14(10):965-980.
[14]熊会元,宗志坚,许铀.线结构光视觉传感器直接标定方法 [J].传感器与微系统,2009,28(3):38-41.
XIONG Hui-yuan,ZONG Zhi-jian,XU You.Direct calibration method of structured light stripe visual sensor [J].Transducer and Microsystem Technologies,2009,28(3):38-41.
[15]邹媛媛,赵明扬,张雷.基于量块的线结构光视觉传感器直接标定方法 [J].中国激光,2014,41(11):195-200.
ZOU Yuan-yuan,ZHAO Ming-yang,ZHANG Lei.Direct calibration method of laser stripe vision sensor based on gauge block [J].Chinese Journal of Lasers,2014,41(11):195-200.
[16]LIU Z,LI X,LI F,et al.Calibration method for line-structured light vision sensor based on a single ball target [J].Optics and Lasers in Engineering,2015,69:20-28.
[17]胡曙光,陈静,华艳秋,等.基于激光三角法的传感器设计 [J].测控技术,2006,25(6):7-12.
HU Shu-guang,CHEN Jing,HUA Yan-qiu,et al.Design of sensor based on laser trigonometry [J].Measurement and Control Technology,2006,25(6):7-12.
[18]贾波,苏显渝,郭履容.采用激光光刀的叶片三维面形测量方法 [J].中国激光,1992,19(4):271-275.
JIA Bo,SU Xian-yu,GUO Fu-rong.3-D measurement of turbine blade profile by light knife [J].Chinese Journal of Lasers,1992,19(4):271-275.
责任编辑:牛晓光
A New Calibration Method for Line-Structured Light Vision Sensor
Based on Linear Scale
KUANGYong-congCUILiang-chun
(School of Mechanical and Automotive Engineering, South China University of Technology, Guangzhou 510640, Guangdong, China)
Abstract:In order to realize a simple, rapid and high accuracy calibration of line-structured light vision sensors, a new direct calibration method of line-structured light vision sensors on the basis of linear scale is proposed, and a planar target and an extraction algorithm of feature point are designed. In the method, by achieving the image coordinates of feature points in the known 3-D coordinates, a subpixel index table is established, and direct calibration of system is realized. The results of calibration and measurement experiments demonstrate that the new calibration method is simple to operation and easy to implement, and is of a high accuracy, specifically, its average measurement error is 0.004 5 mm in Z axis and 0.013 0 mm in X axis. Overall, the new method can meet the requirements of industrial production and measurement.
Key words:line-structured light; vision sensor; calibration; feature point extraction; 3-D measurement
doi:10.3969/j.issn.1000-565X.2016.01.011
中图分类号:TP212.14;TP202
作者简介:邝泳聪(1970-),男, 博士,副教授,主要从事机器视觉、精密制造等研究.E-mail:yckuang@scut.edu.cn
*基金项目:国家“863”计划项目(2012AA050302);粤港关键领域重点突破项目(东莞专项2012205122)
收稿日期:2015-06-08
文章编号:1000-565X(2016)01- 0071- 07
Foundation items: Supported by the National High-tech R&D Program of China (863 Program) (2012AA050302)and the Guangdong & Hongkong Priority Breakthrough Program in Key Areas(Dongguan2012205122)

