一种用于三角形连接绕组的改进型SVPWM算法的研究

周卫华，刘卫国，谭 博

(西北工业大学，西安 710072)

一种用于三角形连接绕组的改进型SVPWM算法的研究

周卫华，刘卫国，谭 博

(西北工业大学，西安 710072)

星形连接绕组的传统SVPWM算法之前已有大量研究。在分析传统SVPWM算法的基础上提出了一种用于三角形连接绕组的改进型SVPWM算法，推导了改进型SVPWM算法并在Simulink环境下搭建了采用该新算法的绕组三角形连接方式的三相混合式步进电机细分驱动系统的仿真模型。并基于DSP芯片TMS320F28335对该算法进行了试验。改进型SVPWM模块和三相混合式步进电机相电流在不同细分数下的仿真和实验波形与理论分析相符。结果验证了该算法的正确性和对三相混合式步进电机细分驱动系统的适用性。

SVPWM；三角形连接绕组；三相混合式步进电机；细分

0 引 言

三相混合式步进电机作为机电系统的输出执行元件，具有结构简单、价格低廉、控制容易、无积累误差、转子角位移与输入脉冲成严格正比等优点，因此三相混合式步进电机广泛用于无机械减速装置的直接驱动控制场合[1-2]。由于制造工艺水平的限制，步进电机的相数和转子齿数不能无限制的增大，从而导致固有步距角较大，不能直接用于高精度伺服控制系统。细分驱动技术使得步进电机可以克服自身的限制，减小步距角，提高步进电机的运行平稳性和精度，抑制了震荡、失步和高噪声现象[3]。SVPWM技术通过对逆变器空间矢量的切换来获得标准圆形磁场，因其谐波少、电压利用率高、编程简单、易于微处理器实现，简化了电路设计，提高了系统的可靠性和实时性，所以广泛应用于永磁同步电机伺服系统中[4]。混合式步进电机从原理上讲可看作低速下的永磁同步电机，可以利用SVPWM技术能在任意空间角度对定子磁链进行定位的性能对混合式步进电机进行细分驱动[5]。现有大多数文献资料给出的电路结构和实验结果都是针对绕组定子绕组星形接法，而对三角形接法研究甚少。以中国电器科学研究院的谭建成为主的学者对绕组连接拓扑结构进行了系列的研究[6-11]，但是这些研究主要集中在无刷直流电机的不同绕组连接方式的性能对比，而对三角形连接的绕组的控制策略未做深入研究，针对三相混合式步进电机定子绕组三角形接法的控制策略研究更少。本文将应用于星形连接绕组的SVPWM算法通过改进应用到三角形连接绕组，并将改进的SVPWM算法应用到绕组三角形连接的三相混合式步进电机脉冲细分驱动控制系统中，最后给出了仿真和实验结果，表明了算法的正确性。

1 用于三角形连接绕组的改进型SVPWM算法

1.1 SVPWM原理及其常规算法

电机的相电压取决于三相逆变器上下桥臂功率管的开关状态，三相逆变电路如图1所示，假设所用功率管均为理想开关器件，定义开关量Si(i=A,B,C)分别为A,B,C相的开关状态，并当i(i=A,B,C)相上桥臂导通时Si=1，反之Si=0。则三相逆变桥共有8种开关状态Vs0～Vs7，其中Vs1～Vs6为工作矢量，Vs0和Vs7为零矢量[12]。8个基本电压矢量空间分布示意图如图2所示。

图1 三相逆变电路示意图

图2 星形连接绕组基本空间电压矢量示意图

根据矢量合成原理，空间任意角度的电压矢量均可以通过其所在扇区两侧的两个基本电压矢量合成得到。根据伏秒平衡原理，只需要满足式(1)，在PWM周期T内目标电压矢量Vref作用效果与相邻两基本电压矢量Vx,Vy分别作用时间Tx和Ty作用效果相同[13]。

VrefT=VxTx+VyTy

(1)

根据以上分析可知，常规SVPWM算法包括扇区的判断、基本电压矢量的选择及其作用时间的确定和电压空间矢量切换点的计算。SVPWM算法原理框图如图3所示[14]。

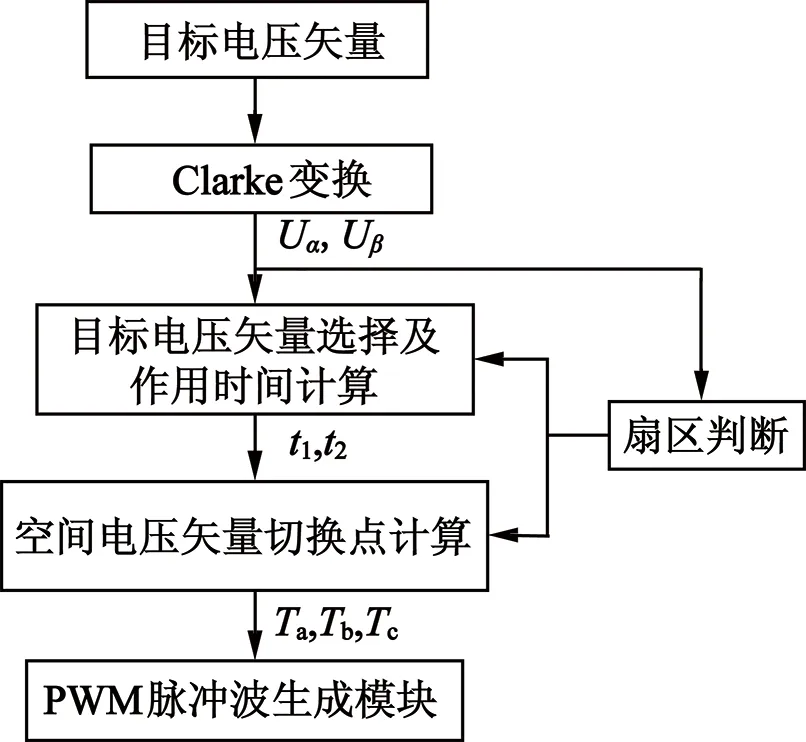
图3 SVPWM算法原理框图

目标电压矢量经过Clarke变换得到两相静止坐标系下的α轴和β轴分量Uα和Uβ，Uα和Uβ根据扇区判断模块计算出目标电压矢量所处扇区，根据求取的扇区号并结合Uα和Uβ可选取两个基本电压矢量并求得其作用时间，进一步求得空间电压矢量切换点，即三相逆变器各功率管的通断时间。

1.2 改进型SVPWM算法

三角形连接绕组内部结构示意图及坐标定义如图4所示。

仿照图2可以得到针对三角形连接绕组的8个空间电压矢量示意图，如图5所示。

图4 三角形连接绕组内部结构及坐标定义示意图

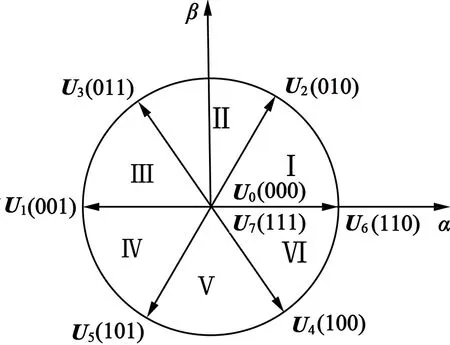
图5 三角形连接绕组基本空间电压矢量示意图

对比图2和图5，不难发现三角形连接绕组的8个基本空间电压矢量相对于星形连接绕组的空间矢量整体顺时针旋转30°电角度，显然传统的SVPWM算法已不再适用，本文将在传统的SVPWM算法的基础上推导出适用于三角形连接绕组的SVPWM算法。

1.2.1 扇区判断模块

表1 扇区号N与P的对应关系

1.2.2 基本电压矢量的选择及其作用时间的确定

表2 相邻两空间电压矢量作用时间表

由基本电压矢量作用时间T1和T2求取电压空间矢量切换点Tcm1,Tcm2,Tcm3的计算方法与传统的SVPWM算法一致，这里不再赘述。在软件中将电压矢量切换点值写到DSP比较寄存器中即可实现对功率管的通断控制即完成了SVPWM算法[15]。

2 仿真分析与试验验证

MATLAB软件包中的Simulink提供了大量的可以实现基本功能的标准模块，能很方便地搭建控制系统仿真模型[16-18]。图6为基于MATLAB/Simulink平台的三相混合式步进电机电流闭环控制系统仿真模型。

图6 三相混合式步进电机脉冲细分驱动仿真图

2.1 改进型SVPWM算法仿真验证

搭建的SVPWM模块内部各个环节如图7所示。其中T=0.002 s,Udc=310 V,Uα和Uβ即为目标电压矢量在两相静止坐标系中α轴和β轴分量。

图7 SVPWM内部仿真图

仿真结果如图8所示。图8(a)中P值变化规律为7-5-4-0-2-3，结合表1可以看出扇区变化规律为Ⅰ-Ⅱ-Ⅲ-Ⅳ-Ⅴ-Ⅵ，说明该模型可以正确判断目标电压矢量所处扇区号，验证了算法的正确性。另外基础电压矢量作用时间和电压矢量切换点分别为三角波和马鞍波，与理论相符。

(a)扇区模块仿真波形(b)基础电压矢量作用时间仿真波形

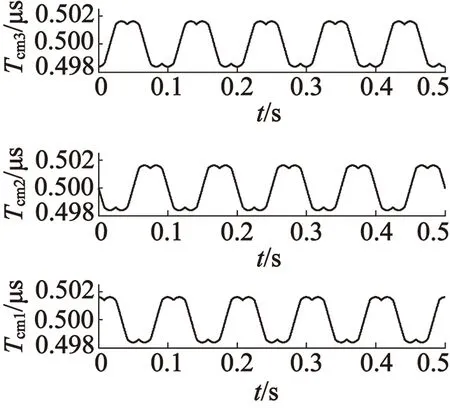
(c) 电压矢量切换点仿真波形

2.2 三角形连接绕组电流细分波形仿真分析与试验验证

实验以绕组三角形连接方式的三相混合式步进电机为研究对象,转子齿数为50，采用DSP芯片TMS320F28335作为控制核心,电压型逆变电路作为主本，IR公司的智能功率模块IPM作为功率器件,组成一个闭环控制系统，并使用恒转矩、等步距角电流细分驱动控制方法。仿真和实验波形如图9所示。

(a) 四细分下的电流波形

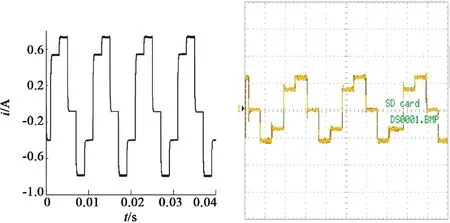
(b) 五细分下的电流波形

(c) 八细分下的电流波形

(d) 二十细分下的电流波形

(e) 一千细分下的电流波形

图9 不同细分数下的电流仿真和实验波形

图9中细分数确定时相电流仿真和实验波形相同，并且随着细分数的增加，相电流波形愈趋近于正弦波，与理论相符，验证了改进型SVPWM算法的正确性以及对三相混合式步进电机的适用性。

3 结 语

SVPWM技术因其编程简单、易于处理器实现、可简化硬件电路等优点广泛应于现代电机伺服系统中。本文在分析传统SVPWM原理及其算法的基础上，推导出了针对绕组三角形连接方式的改进型SVPWM算法。该算法针对8个基本电压矢量相对于两相静止坐标系顺时针旋转30°电角度的问题对扇区判断模块、基本电压矢量的选取和作用时间的确定模块进行了相应的改进。并将改进型SVPWM算法应用到绕组三角形连接的三相混合式步进电机脉冲细分驱动控制系统并进行仿真和实验验证，结果表明了本文所提改进型算法的科学性和有效性。

[1] 史敬灼,徐殿国,王宗培.混合式步进电动机伺服系统研究[J].电工技术学报,2006,21(4):72-78.

[2] 刘景林,王帅夫.数控机床用多步进电机伺服系统控制[J].电机与控制学报,2013,17(5):80-86.

[3] JUNMEI X,GAOHUAaohua L,WU Y.Study of stepping motor subdivision driver[C]//2010 International Conference on Intelligent Computation Technology and Automation (ICICTA).2010:443-446.

[4] 程树康,高晗璎,孙力.两相混合式同步电动机的SVPWM控制[J].中国电机工程学报,2003,23(2):97-102.

[5] 苏义鑫,孙功武,聂巍.基于矢量控制的步进电动机细分驱动技术[J].微特电机,2014,42(2): 56-59.

[6] 曹春.无刷直流电动机绕组接法的比较分析[J].微特电机,2008,36(2):24-25.

[7] 谭建成.三相无刷直流电动机分数槽集中绕组槽极数组合规律研究(连载之八)[J].微电机,2008,41(7):52-55.

[8] 韩光鲜,王宗培,程智,等.无刷直流电动机定子绕组的星形和三角形联接[J].微电机(伺服技术),2003,36(1):3-6.

[9] 王宗培,陈敏祥.关于直流电动机的电枢绕组及电枢电路(一)环流问题[J].微电机,2012,45(7):1-5.

[10] 谭建成.多相永磁电机封闭形绕组无环流条件的分析[J].微电机,2013,46(4):1-7.

[11] 谭建成.多相无刷直流电机绕组拓扑结构的探讨[J].微电机,2013,46(10):1-4.

[12] 杨贵杰,孙力,崔乃政,等.空间矢量脉宽调制方法的研究[J].中国电机工程学报,2001,21(5):80-84.

[13] 邢绍邦,罗印升,沈琳.一种新颖的SVPWM算法及其仿真[J].系统仿真学报,2013,25(1):190-194.

[14] 贺虎成,肖杰,赵熙,等.VVVF控制用SVPWM算法设计[J].微特电机,2015,43(4): 68-69.

[15] 吴丽华,高慧芝,刘政,等.一种改进型的SVPWM算法研究[J].电机与控制学报,2013,17(4): 57-63.

[16] GRIMBLEBY J B.Simple algorithm for closed-loop control of stepping motors[J].IEE Proceedings,Electric Power Applications,1995,142(1):5-13.

[17] 刘卫国,宋受俊.三相反应式步进电动机建模及常用控制方法仿真[J].微电机,2007,40(8): 22-25.

[18] 徐杜,蒋永平,周韶勇,等.全数字式步进电机连续细分方法与实现[J].微特电机,1997,25(2):25-29.

[19] 刁红泉.基于DSP的三相混合式步进电机脉冲细分驱动系统[D].杭州：浙江大学,2005.

Study on an Improved SVPWM Algorithm for △-Connected Windings

ZHOUWei-hua，LIUWei-guo，TANBo

(Northwestern Polytechnical University,Xi’an 710072,China)

Considerable research on conventional SVPWM algorithm has been done for Y-connected windings. An improved SVPWM algorithm for △-connected windings was presented based on the analysis of conventional SVPWM theory. The improved SVPWM algorithm was deduced and the subdivision drive control system of a three-phase hybrid stepping motor with △-connected windings was built by Simulink. Experiments about the improved algorithm are completed based on DSP controller TMS320F28335. The simulation and experiment waveforms of the improved SVPWM module and phase currents of the three-phase hybrid stepping motor accord with theoretical analysis results. The results verify the correctness of this algorithm and applicability to the subdivision drive control system of the three-phase hybrid stepping motor.

SVPWM; △-connected windings; three-phase hybrid stepping motor; subdivision

2015-10-12

张惠国(1978-)，男，博士，副教授，主要研究方向为功率器件及应用、集成电路设计。

TM383.6

A

1004-7018(2016)12-0102-04