基于Copula函数的风电场风速建模分析
刘文霞,何向刚,钟以林,李雪凌
(贵州电网有限责任公司电网规划研究中心,贵州贵阳 550003)
Modelling Analysis on Wind Speed of Farm Based on Copula FunctionLIU Wenxia, HE Xianggang, ZHONG Yilin, LI Xueling
(Grid Planning & Research Center, Guizhou Power Grid Co., LTD, CSG., Guiyang 550003, China)
基于Copula函数的风电场风速建模分析
刘文霞,何向刚,钟以林,李雪凌
(贵州电网有限责任公司电网规划研究中心,贵州贵阳550003)
Modelling Analysis on Wind Speed of Farm Based on Copula FunctionLIU Wenxia, HE Xianggang, ZHONG Yilin, LI Xueling
(Grid Planning & Research Center, Guizhou Power Grid Co., LTD, CSG., Guiyang 550003, China)
0引言
风能是一种绿色清洁能源,做好风速建模及风速预测工作,可为分析风速特性对电网安全稳定影响、风电消纳、风电场规划选址等问题提供有力的帮助及相关技术支撑。当前风速建模预测方法可分为基于物理模型和基于历史数据这两种。前者一般采用数值天气预报数据进行风速预测,后者是利用历史风速进行外推预测。风力资源分布具有一定地域特性,但现阶段风速建模研究中大多未考虑同一风场内部不同位置风速的相关性,而是假设风场内各风机所处位置的风速在同一时刻相等[1-2]。对于大型风电场或山区风电场(如贵州毕节赫章的韭菜坪风电场),该假设显然没有反映出风场内部风速具有相关性这一特点。由于风场内部风速相关性直接影响风场出力,进而影响系统电量分配及安全运行,因此要做好风电场规划选址、风电消纳工作、含风电场电力系统的安全稳定性分析及经济性分析,就必须要建立拟合度较好的风电场风速相关性模型。
目前常用来处理风速相关性的方法主要有3种。一是基于自回归滑动平均模型和时移技术法建立时间序列相关性的风速序列[3];二是基于线性相关系数矩阵的Cholesky分解的正交变换法[4-6];三是考虑风速线性相关矩阵与标准正态分布变量线性相关矩阵关系的Nataf变换方法[7-10]。这3种方法都假设具有相关性的风速序列满足同参数的分布,例如假设都满足同样的威布尔分布参数。但实际风场的风速常呈现不同的分布,即使建模认为分布类型相同,分布参数也不一样。Copula函数的秩相关度量方法能够很好地解决上述问题。Copula函数在金融问题研究方面已得到应用[11-12]。在电力系统方面,文献[13-14]基于Copula函数提出了电力线和铁塔冰荷载、风荷载的联合概率分布计算模型;文献[15]应用Copula函数建立了相依概率性序列运算理论和方法,并将该运算用于多个风电场总出力概率分布分析中;文献[16-17]分别基于实测多个风电场风速及负荷水平的相关性,采用Copula函数建立了计及风场间风速相关性的风速样本及具有相关性的负荷需求样本。文献[18]采用混合Copula函数建立了山区风电场出力模型。
本文基于正态Copula函数,对韭菜坪风电场内部风速的分布特性及所具有的相关性进行建模预测,即通过历史风速的累积概率分布函数建立正态Copula函数,再用秩相关理论建立风场内部风速秩相关矩阵,根据正态Copula函数及风速秩相关矩阵建立了该风电场风速预测模型。通过对比风速建模预测模型与历史统计风速数据的累积概率分布曲线和概率密度曲线,得知所采用的正态Copula函数能较好地预测韭菜坪风电场相关风速。据此,可以将Copula函数建立风电场风速模型推广应用到工程实际中,以指导规划风电场的风速预测、站址选择,也可以应用到在运行的风电场出力建模及安全稳定运行分析中。
1基于Copula函数的风场聚合模型
1.1Copula函数及其基本理论
1.1.1Copula函数
1959年Sklar将一个n维联合分布函数分解为n个边缘分布函数和一个Copula函数。Copula函数可以用来描述变量的相关性,它把随机向量X1,X2,…,Xn的联合分布函数F(x1,x2,…,xn)与各自的边缘分布函数FX1(x1),…,FXn(xn)连接在一起,即函数C(u1,u2,…,un),使:
(1)
假设随机向量U1,U2,…,Un服从[0,1]之间的均匀分布,则随机向量X1,X2,…,Xn的边缘分布函数FX1(x1),…,FXn(xn)可记为[16-17]:
(2)
式中:ui为向量Ui中的元素。对边缘概率分布函数(累积概率分布函数)FXi(xi)作等概率逆变换:
(3)
则式(1)可写为
(4)
1.1.2多元正态Copula函数
以下基于多元正态Copula函数建立风场内部相关风速模型,n元正态Copula分布函数:
(5)
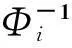
1.2Spearman秩相关系数
度量随机变量相关性的方法有很多种,线性相关度是常用的指标之一,其定义为
(6)
式中:ρRL表示随机变量X1、X2之间的线性相关度;cov(•)表示求协方差;var(•)表示求方差。
线性相关度仅反映了随机变量之间的线性相关性,如果对随机变量进行单调性相同的线性变换,则其线性相关度不变,但若对其进行单调的非线性变换,则其线性相关度将发生改变。为了避免对风速作非线性变换时采用线性相关来度量相关性出现偏差,本文将采用Spearman秩相关的方法来计算风场内部风速的相关性。
随机向量X、Y的Spearman秩相关系数ρRr定义如下,设有随机变量(xj,yj|j=1,2,…,m)是随机向量X、Y中的元素,对X、Y中的元素进行排序,得到随机向量中元素(xj,yj|j=1,2,…,m)的秩(XRj,YRj),则:
(7)
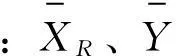
假设有风速序列(采样时间间隔是1min,采样总时间10min)vS1、vS2;风机出力特性分段拟合函数式为(8),切入风速是3m/s,切出风速是25m/s,额定风速为14m/s;将风速序列带入风机出力特性拟合函数得到风机出力Pw1、Pw2,该过程实际是对风速序列做单调非线性变换。
(8)
vwi、vwo为切入、切出风速;vr是额定风速;Pr是风机额定出力(本文为1.5MW);t为风速-功率系数,本文取为3。
表1显示了风速序列vS1、vS2及其秩R1、R2,风机出力Pw1、Pw2及其秩r1、r2,对表1中风速序列求得线性相关度为0.872 6,风机出力线性相关度为0.859 8;对风速序列求得秩相关度为0.818 2,风机出力秩相关度也为0.818 2,可见,风速与风机出力的秩相关度相等。基于上述结论,本文利用Spearman秩相关这一优良特性度量风场内部风速相关性。
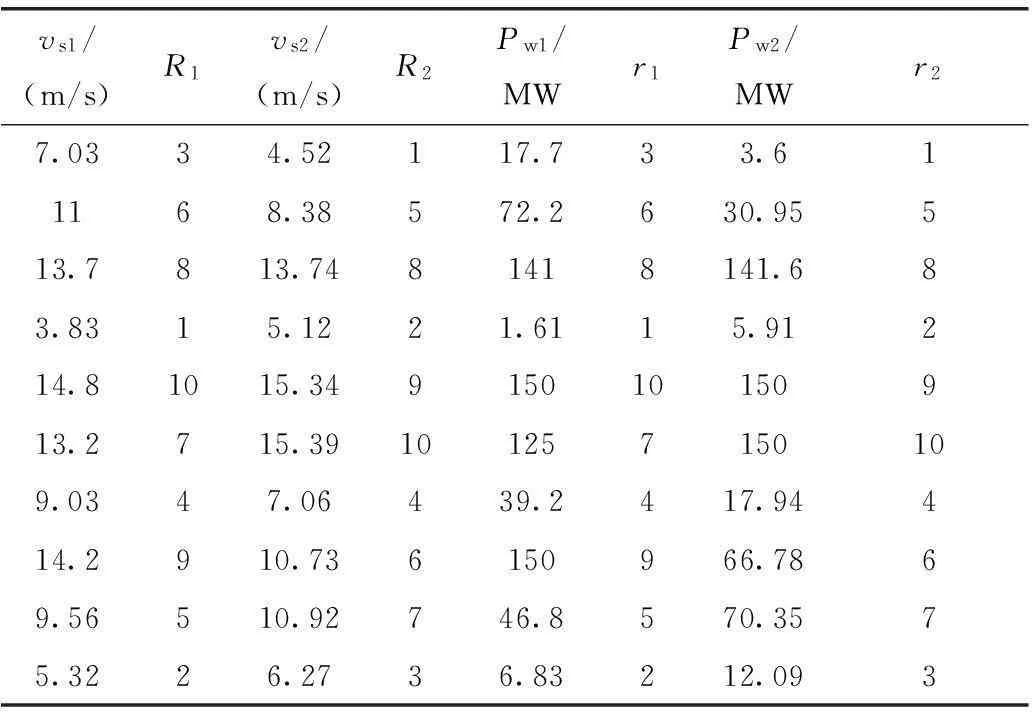
表1 风速及风机出力的秩
2基于Copula函数及秩相关理论的风速建模
本文根据韭菜坪风电场2012年8月~2013年7月间每月典型日的各台风机历史风速实测数据,采用Copula函数建立其相关风速模型。该风场共56台风机,单机容量1.5MW,总装机84MW,本次建模将按照该风电场风机编号8组,每组风机群包含7台风机。
建模时对风电场历史记录风速作非线性变换,即设风速为服从威布尔分布,将此样本通过风速的累积分布函数变换到均匀分布空间,然后用式(5),通过多元正态Copula函数将均匀分布空间变换到标准正态分布空间,建立起风场内部的相关风速模型。
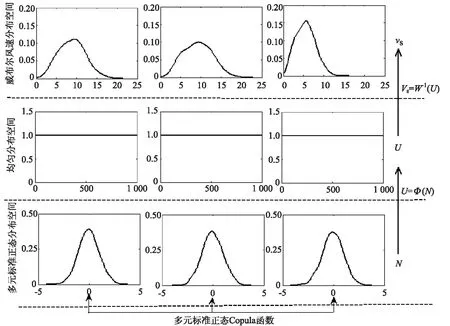
图1 正态Copula函数变换过程示意图
3个样本空间变换关系如图1所示[19],图中VS表示风速样本,W-1(•)为威布尔分布函数的逆函数,N为多元标准正态分布的随机变量。
3计算流程
计算过程如下:首先对韭菜坪风电场2012年8月~2013年7月一年内的历史风速进行采样,并求得历史记录风速的秩相关矩阵及威布尔分布参数;其次采用多元正态Copula函数建立风场内部各机群的相关风速样本,最后对比分析历史风速和预测建模风速的概率统计信息(风速累积概率分布曲线和概率密度曲线),以验证所采用多元正态Copula函数的实用性。计算过程详见图2。
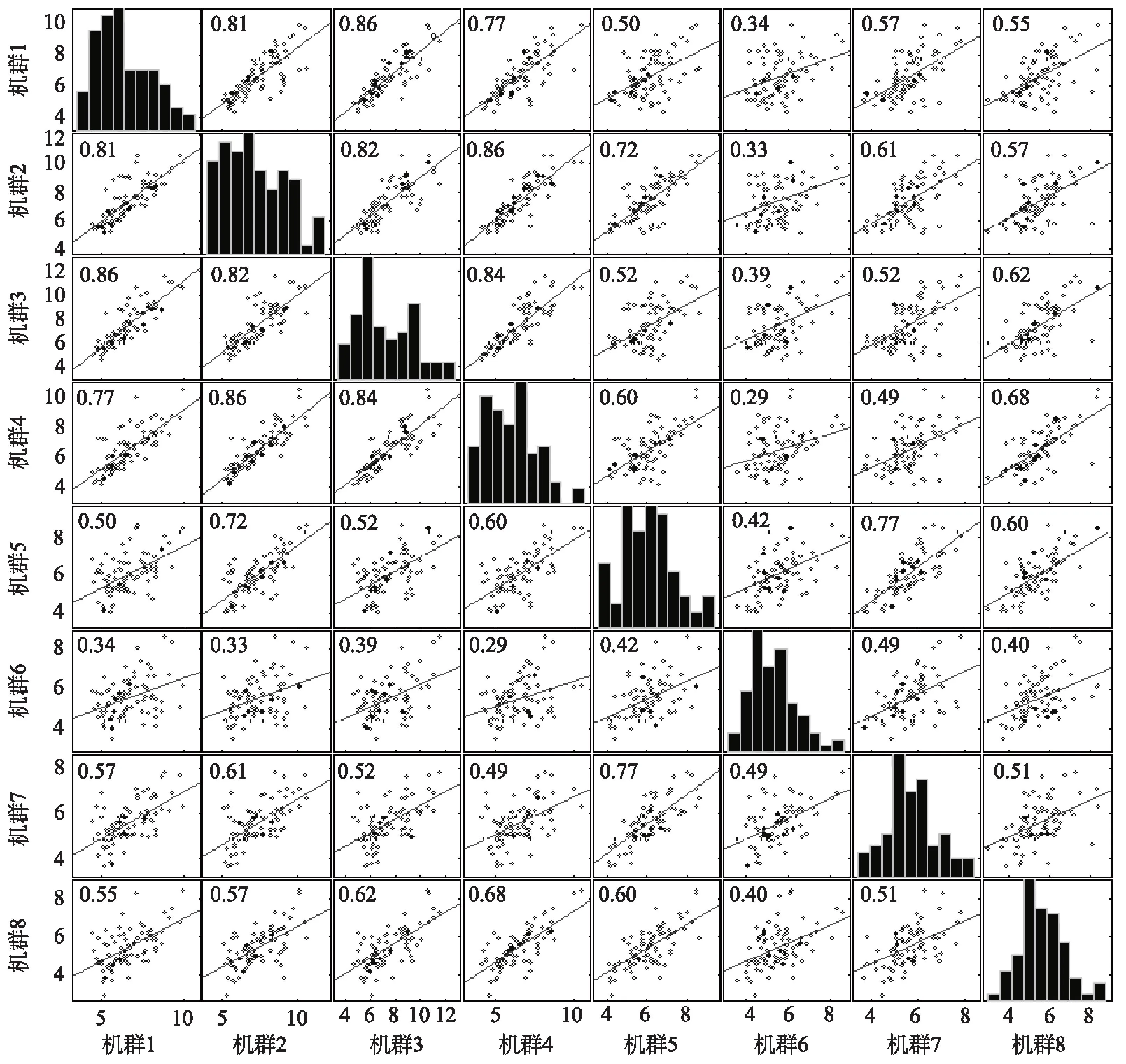
图3 各风机群历史风速分布秩相关矩阵
4算例分析
本文对韭菜坪风电场的风速进行预测建模。首先对历史风速样本空间求取Spearman秩相关矩阵,如图3为该风电场8个机群之间历史记录风速的秩相关矩阵图,对角线子图显示各个风机群风速所服从的威布尔分布(秩相关矩阵的对角元素一定为1,表示各个机群的风速与自身的秩相关度为1),非对角元素表示每两个风机群之间的风速秩相关度,例如第一行第二列表示风机群1与风机群2的秩相关为0.81,可见,风场内部各风机群的风速具有一定的相关性。
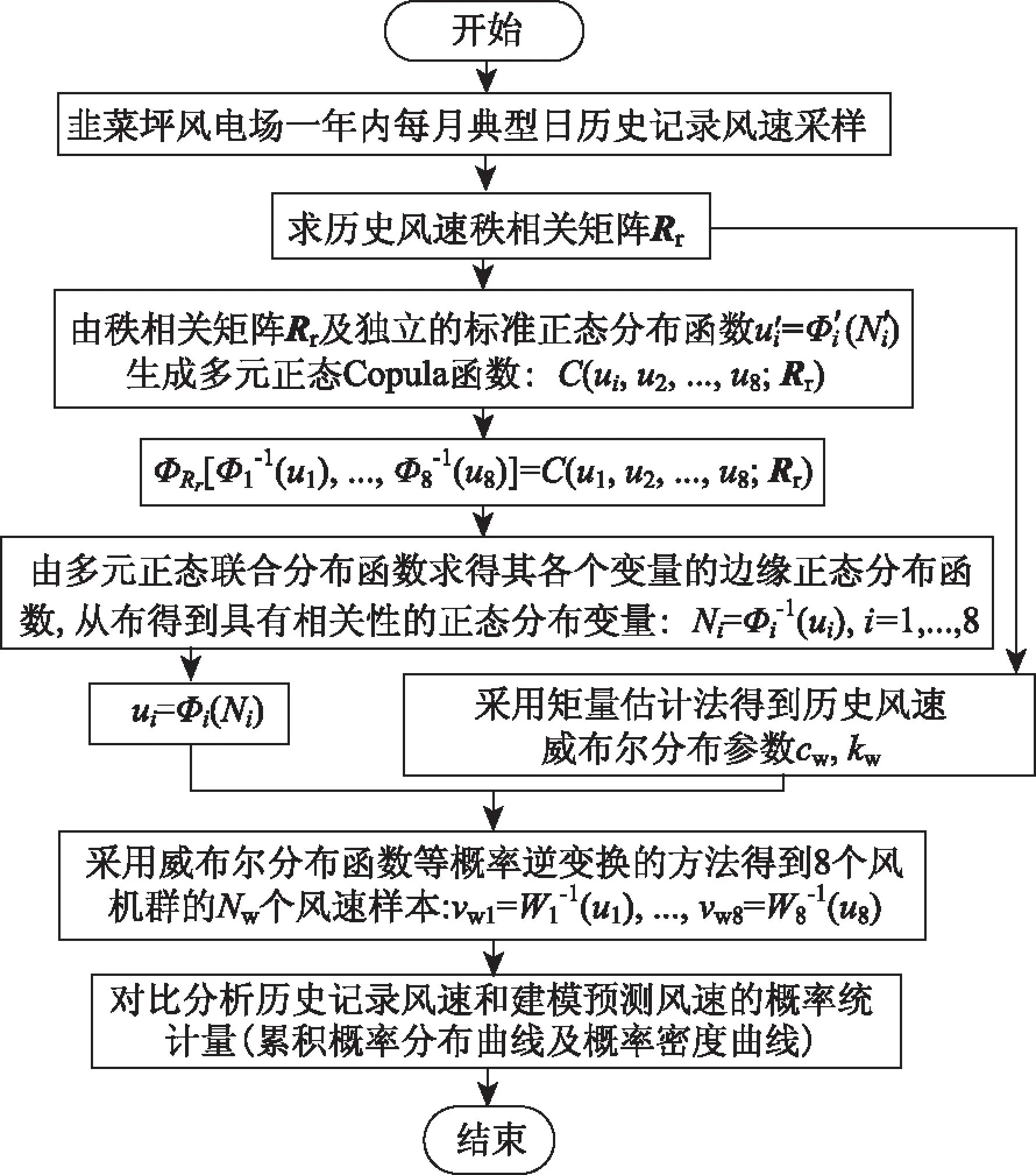
图2 计算流程图
在拟合该风电场8个风机群的历史记录风速样本分布时,假设风速服从威布尔分布[20-23],如式(9),并通过矩量估计法[22]得到威布尔分布参数,如表2所示。
(9)
式中:vw是风速;cw和kw分别为尺度参数和形状参数;cw反映所描述地区的年平均风速大小。
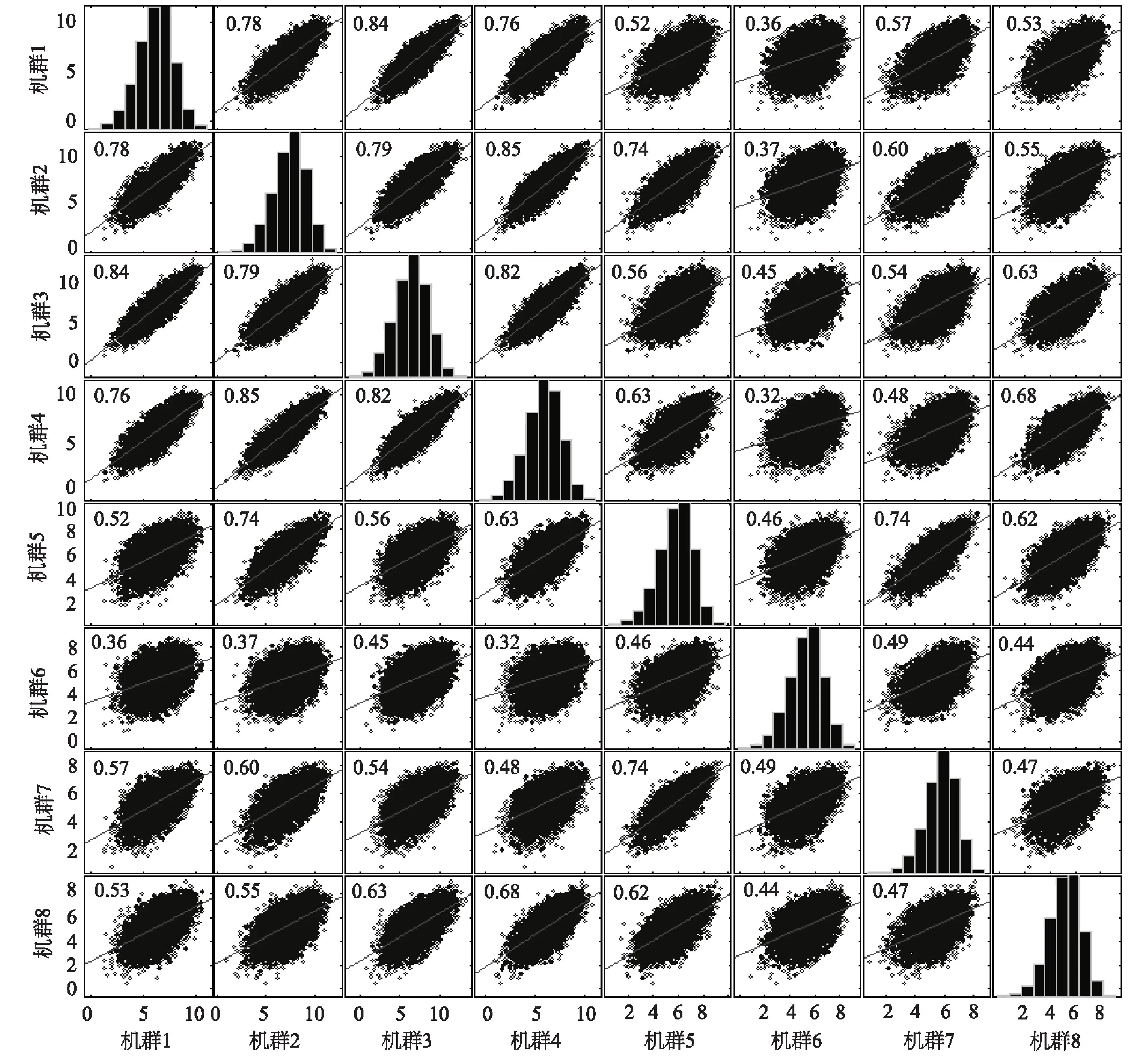
图4 各风机群预测风速分布秩相关矩阵
采用多元正态Copula函数,建立韭菜坪风电场风速预测模型,设风速预测样本为10 000,得到所建模预测的相关风速秩相关矩阵如图4所示,对比图3可以看出,所建模预测的风速与韭菜坪风电场历史记录风速的秩相关矩阵基本相等。
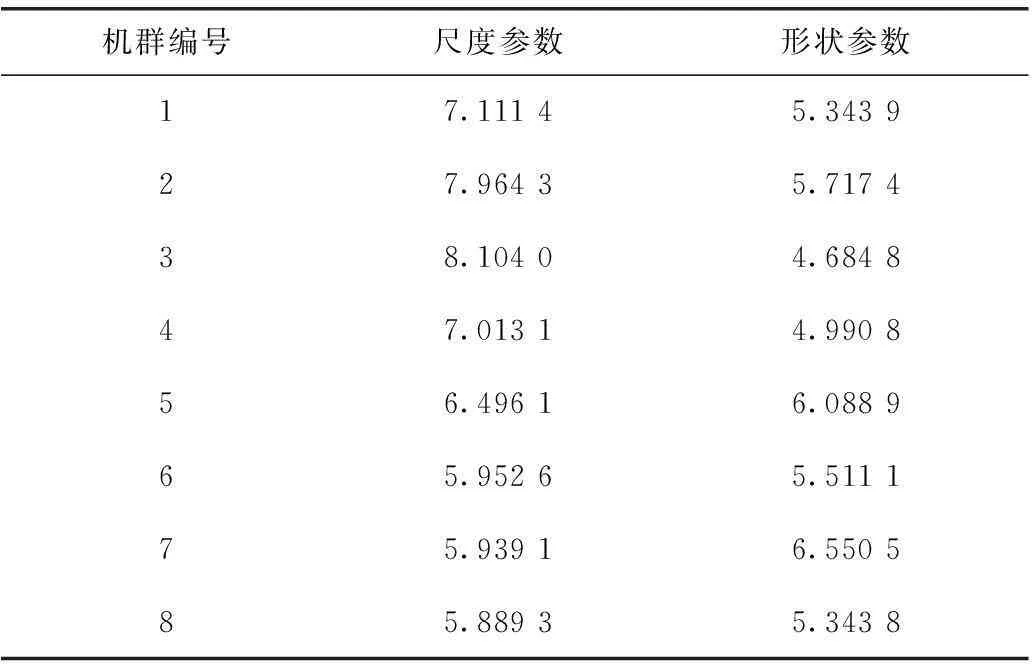
表2 韭菜坪风电场风速威布尔分布参数
图5显示了建模预测风速与历史记录风速的累计概率分布曲线,图6为概率密度曲线。显然,历史记录风速的累积概率分布与预测建模风速的累积概率分布曲线基本重合,显示了所采用多元正态Copula函数建模的较高准确度。在风速概率密度曲线中,历史记录风速分布较预测风速概率曲线略微“陡峭”,实际上是由于历史风速取的是每个月的典型日风速,所以风速分布会显得相对“集中”。
综合对比历史记录风速和建模预测风速秩相关矩阵和概率统计曲线,可以看出本文所采用的方法有较高的拟合预测精度。
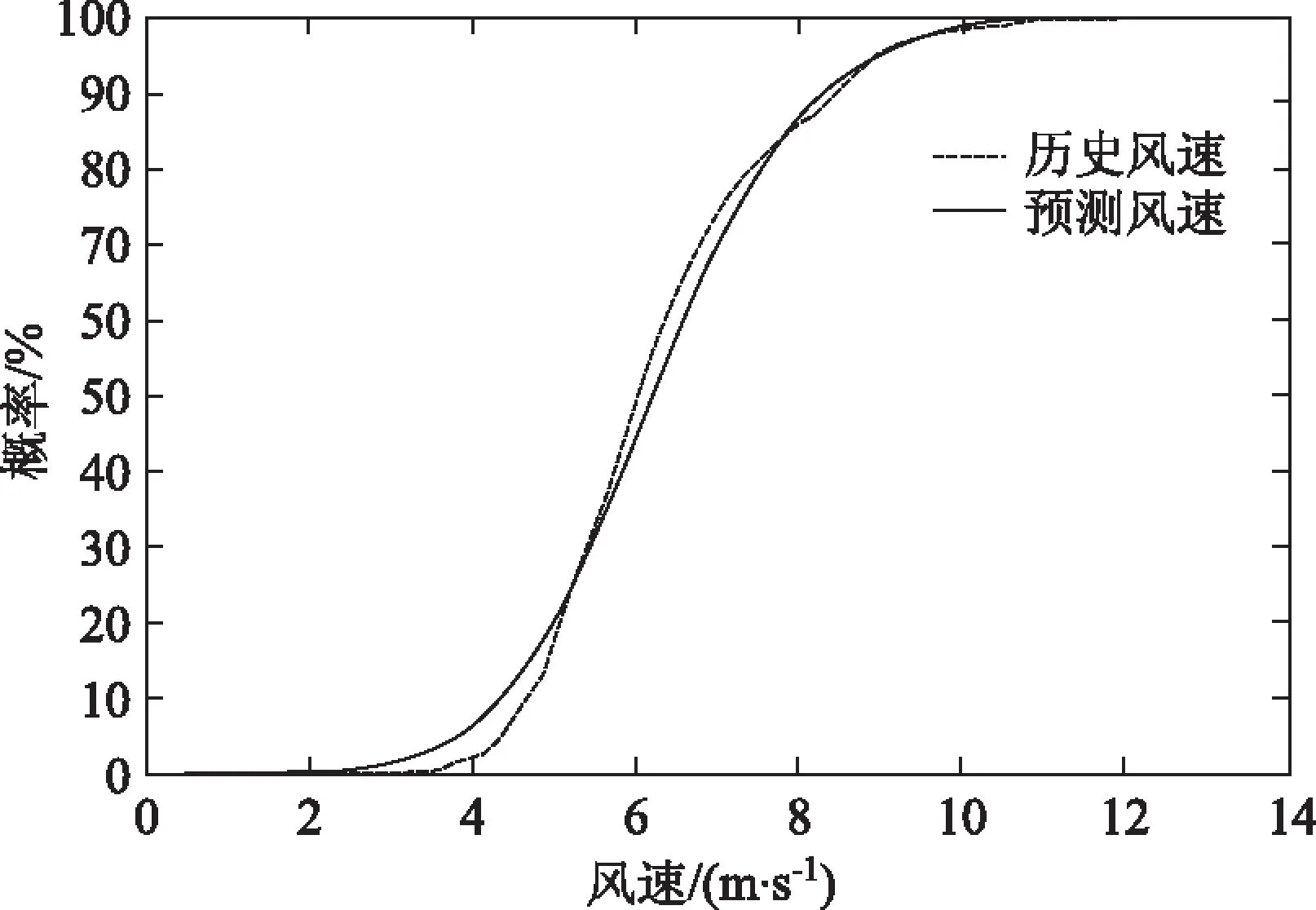
图5 风速累积概率分布曲线

图6 风速概率密度曲线
5结束语
建模分析结果显示,秩相关矩阵能够较好地描述风电场内部机组之间风速的相关特性,通过多元正态Copula函数建模预测的风速与历史风速的概率统计特性比较贴近,体现了该方法的较高准确度。进而可以考虑将本方法推广应用到贵州电网大型风电场及山区风电场的风速建模计算中,以进一步提高风速预测的精度,从而为贵州省风电场规划选址、电网安全稳定及经济运行提供一定的技术支持。
参考文献
[1]孙元章,吴俊,李国杰,等.基于风速预测和随机规划的含风电场电力系统动态经济调度[J].中国电机工程学报,2009,29(4):41-47.
[2]叶林,刘鹏.基于经验模态分解和支持向量机的短期风电功率组合预测模型[J].中国电机工程学报,2011,31(31):102-108.
[3]范荣奇,陈金富,段献忠,等.风速相关性对概率潮流计算的影响分析[J].电力系统自动化,2011,35(4):18-22.
[4]Edwin Haesen,Cindy Bastiaensen,Johan Driesen,et al.A Probabilistic Formulation of Load Margins in Power Systems With Stochastic Generation[J].IEEE Trans. on Power Systems,2009,24(2):951-958.
[5]张粒子,凡鹏飞,麻秀范,等.考虑调峰适应性风险的风电场群时序规划方法[J].中国电机工程学报,2012,32(7):14-22.
[6]鲍海波,韦化.考虑风电的电压稳定概率评估的随机响应面法[J].中国电机工程学报,2012,32(13):77-85.
[7]潘雄,周明,孔晓民,等.风速相关性对最优潮流的影响[J].电力系统自动化,2013,37(6):37-41.
[8]Juan M Morales,Antonio J Conejo,Juan Pérez-Ruiz.Simulating the Impact of Wind Production on Locational Marginal Prices[J].IEEE Trans. on Power Systems,2011,26(2):820-828.
[9]Juan M Morales,L Baringo,Antonio J Conejo,et al.Probabilistic power flow with correlated wind sources [J].IET Generation, Transmission & Distribution,2010,4(5):641-651.
[10]潘雄,刘文霞,徐玉琴,等.基于SRSM和Nataf方法的含风场群电力系统暂态稳定分析[J].中国电机工程学报,2013,33(16):56-62.
[11]Umberto Cherubini,Fabio Gobbi,Sabrina Mulinacci,et al.Dynamic Copula Methods in Finance [M].Chichester:Wiley,2011.
[12]Umberto Cherubini,Elisa Luciano,Walter Vecchiato.Copula Methods in Finance [M].Chichester:Wiley,2004.
[13]徐文军,杨洪明,赵俊华,等.冰风暴灾害下电力断线倒塔的概率计算[J].电力系统自动化,2011,35(1): 13-17.
[14]杨洪明,黄拉,何纯芳,等.冰风暴灾害下输电线路故障概率预测[J].电网技术,2012,36(4): 213-218.
[15]张宁,康重庆.风电出力分析中的相依概率性序列运算[J].清华大学学报:自然科学版,2012,52(5):704-709.
[16]George Papaefthymiou,Dorota Kurowicka.Using Copulas for Modeling Stochastic Dependence in Power System Uncertainty Analysis [J].IEEE Trans. on Power Systems,2009,24(1):40-49.
[17]Alicja Lojowska,Dorota Kurowicka,George Papaefthymiou,et al.Stochastic Modeling of Power Demand Due to EVs Using Copula [J].IEEE Trans. on Power Systems,2012,27(4):1960-1968.
[18]潘雄,王莉莉,徐玉琴,等.基于混合Copula函数的风电场出力建模方法[J].电力系统自动化,2014,38(14):17-22.
[19]王俊,蔡兴国,季峰.基于Copula理论的相关随机变量模拟方法[J].中国电机工程学报,2013,33(22):75-82.
[20]Bowden G J,Barker P R,Shestopal V O,et al.The Weibull distribution function and wind power statistics[J].Wind Engineering,1983,7:85-98.
[21]雷亚洲,王伟胜,印永华,等.基于机会约束规划的风电穿透功率极限计算[J].中国电机工程学报,2002,22(5):32-35.
[22]Feijoo A E,Cidras J.Modeling of wind farms in the load flow analysis [J].IEEE Trans. on Power Systems,2000,15(1):110-115.
[23]吴义纯,丁明,张立军.含风电场的电力系统潮流计算[J].中国电机工程学报,2005, 25(4):36-39.

刘文霞(1987—),女,硕士,助理工程师,主要从事电力系统规划设计、分析计算等方面的工作,E-mail: liuwenxia_csggz@126.com;
何向刚(1982—),男,硕士,工程师,主要从事电力系统规划、电力系统可靠性分析工作,E-mail:525153231@qq.com;
钟以林(1971—),男,本科,工程师,主要从事电力系统规划、分析工作,E-mail:310319040@qq.com;
李雪凌(1981—),女,硕士,工程师,主要从事电力系统规划设计、分析计算等方面的工作,E-mail:lixuelinglxl@126.com。
(责任编辑:杨秋霞)
摘要:韭菜坪风电场为贵州省的一个大型山区风电场,风电场内各机组的风速具有一定相关性。本文采用多元正态Copula函数及秩相关矩阵度量的方法来量化分析该风电场内风速的相关性,以建立更能反映该风电场特性的风速模型。多元正态Copula函数能有效地将威布尔分布的风速序列、风速累积概率分布序列及标准正态分布序列连接起来,实现相关风速变量的转换及建模预测。该方法为今后分析韭菜坪风电场风速特性对该地区电网安全稳定性的影响提供一定的技术支持,也可为山区及大型风电场规划选址提供参考。
关键词:Copula函数;风速相关性;秩相关;概率密度
Abstract:Jiucaiping wind farm of Guizhou province locates in a large mountainous area, and the wind speed of each wind turbine in wind farm is always correlative. In this paper, multivariate normal Copula function and rank correlation matrix are used to quantify the coherence of wind speed in the wind farm so as to build the wind speed model which can reflect the wind speed characteristics of the wind farm. The Weibull wind speed distribution, cumulative distribution function of wind speed and multivariate normal distribution sequences can be joined by multivariate normal Copula function effectively, which realizes the transform and modeling prediction of relative wind speed. Furthermore it can provide certain technical support for analyzing the influence of wind speed of Jiucaiping wind farm on the stability of power grid security in this region. It also can provide some references to the planning and development of wind farms in the mountainous area and large wind farms as well.
Keywords:Copula function; wind speed correlation; rank correlation; probability density
作者简介:
收稿日期:2015-05-10
基金项目:国家高技术研究发展计划(863计划)项目(2014AA051902);中国南方电网公司重点科技项目(K-GZ2013-468)
中图分类号:TM743
文献标志码:A
文章编号:1007-2322(2016)02-0070-07

