基于风场景识别的动态风电功率概率预测方法

阎　洁，刘永前，张　浩，张慧玲，冯双磊

(1.新能源电力系统国家重点实验室(华北电力大学)，可再生能源学院，北京　102206;

2.国网宁夏电力公司，宁夏银川　750001；3.中国电力科学研究院，北京　100192)

Dynamic Wind Power Probabilistic Forecasting Based on Wind Scenario RecognitionYAN Jie1, LIU Yongqian1, ZHANG Hao1, ZHANG Huiling2, FENG Shuanglei3

(1.State Key Laboratory of Alternate Electrical Power System with Renewable Energy Sources (School of Renewable Energy),

North China Electric Power University, Beijing102206,China; 2.State Grid Ningxia Electric Power Company,

Yinchuan 750001,China;3.China Electric Power Research Institute, Beijing 100192, China)



基于风场景识别的动态风电功率概率预测方法

阎洁1，刘永前1，张浩1，张慧玲2，冯双磊3

(1.新能源电力系统国家重点实验室(华北电力大学)，可再生能源学院，北京102206;

2.国网宁夏电力公司，宁夏银川750001；3.中国电力科学研究院，北京100192)

Dynamic Wind Power Probabilistic Forecasting Based on Wind Scenario RecognitionYAN Jie1, LIU Yongqian1, ZHANG Hao1, ZHANG Huiling2, FENG Shuanglei3

(1.State Key Laboratory of Alternate Electrical Power System with Renewable Energy Sources (School of Renewable Energy),

North China Electric Power University, Beijing102206,China; 2.State Grid Ningxia Electric Power Company,

Yinchuan 750001,China;3.China Electric Power Research Institute, Beijing 100192, China)

0引言

风力发电是可再生能源发电技术中发展最快和最为成熟的方式。2014年，中国(除台湾地区外)新增风电机组13 121台，新增装机容量23 196MW，同比增长44.2%；累计安装风电机组76 241台，累计装机容量114 609MW，同比增长25.4%[1]。然而风电具有波动性和间歇性，大规模风电接入电网给电力系统的安全和稳定运行以及保证电能质量带来严峻挑战。风电功率预测技术是减轻风电并网带来的负面影响的有效方式之一。准确可靠的风电功率预测对电力系统动态经济调度、增加风电渗透率、减少旋转备用容量、提高风电场容量系数等具有重要意义[2-3]。

很多学者致力于研究风电功率预测算法和优化策略，在实际工程应用中已经取得了较好的效果。人工神经网络是目前短期风电功率单点预测领域应用最为广泛的方法，具有非线性映射能力强、泛化性好的特点[4-7]。尽管如此，在实际工程应用中，短期单点预测的误差约为15%～20%，尚无法满足电力系统优化运行的精度需求。概率预测是单点预测的延伸，提供任意置信水平下风电功率可能的波动范围，补充预测误差的概率性信息。常用方法有：分位数回归法[8-10]、核密度[11-12]、情景模拟法[13-14]等。但上述方法采用固定模型模拟风力发电过程，导致对特定风况的预测精度较低，模型鲁棒性弱。尤其在大规模风电场(群)，风况时空分布特征多样，单一预测模型将更难描述风况复杂多样的变化规律，预测精度也将难以得到提升。

针对上述问题，本文提出了基于风场景识别的风电功率概率预测模型。通过分析自然风短时变化和季节性特征，研究数值天气预报(Numerical weather prediction, NWP)数据对预测误差的敏感程度，选用风速和风向作为划分风场景的参考变量，建立风场景聚类分析模型。每一类风场景代表一种自然风的特征，针对不同特征建立基于相关向量机(Relevance vector machine, RVM)的概率预测模型，提供单点预测结果的同时，补充任意置信水平下风电功率可能的波动范围。在预测时根据实际风况实时判断所属的风场景类别，动态调用该场景下的模型参数来进行概率预测。引用中国西北某风电场的实际运行数据，验证风场景识别在概率预测中的应用效果，采用基于人工神经网络的单点预测模型进行误差对比分析，利用基于分位数回归算法的概率预测模型进行概率预测可靠性和技术分数的对比。结果表明：基于风场景识别的概率预测算法有效提高了模型的可靠性和精度。

1风特性分析

由风电机组功率曲线可知，风速是影响风电场发电特性的最主要因素，而不同时间内风速波动的频率和幅度有很大区别，加剧了风速影响的程度。图1为中国西北某风电场5月到7月的风速波动情况，该段时间内风电场平均风速为5.86m/s，最大风速17.79m/s，最小风速0.07m/s。

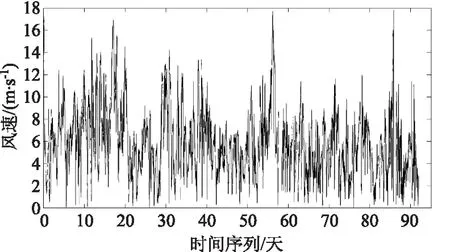
图1　西北某风电场5月到7月份风速图

风向也是影响风电场输出功率的重要因素，不同季节内风向的频率分布迥异。图2～图5为该风电场4个季节的风向玫瑰图。可见，11月到1月的主导风向为北风与东北风；2月到4月主要为西北风，5月到7月主要为西风与西南风，8月到10月主要为西风与北风。

由于受到大气湍流、尾流效应、塔影效应的影响，风电机组轮毂高处附近的风场往往是不均匀的，导致风力发电机组在指定风速下达不到理论功率曲线预期的功率。此外，根据热力学理论，气温、压力、相对湿度等天气因素会导致空气密度的变化，这也将影响风电场输出功率。

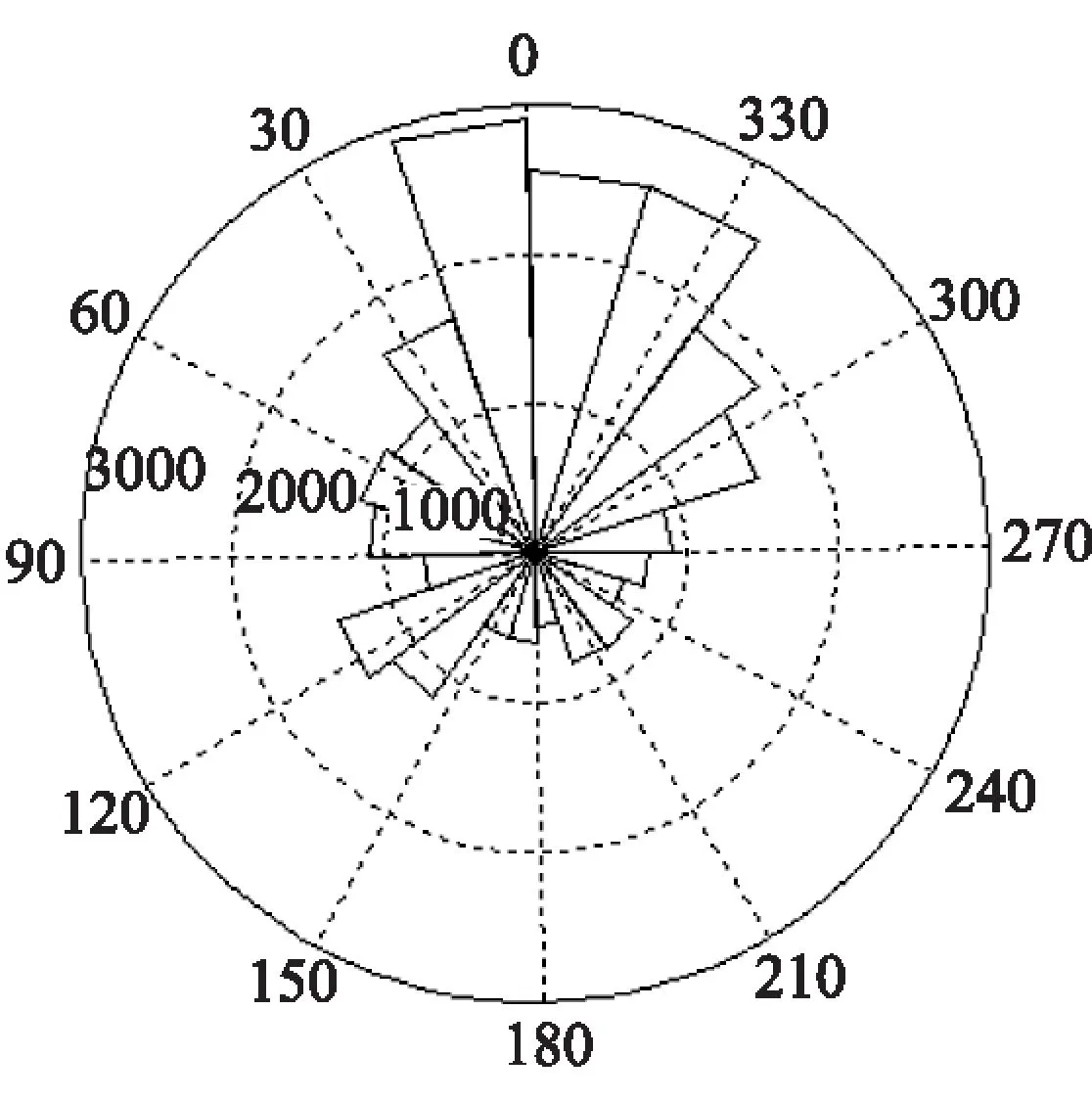
图2　西北某风电场11月到1月风向玫瑰图

图3　西北某风电场2月到4月风向玫瑰图

图4　西北某风电场5月到7月风向玫瑰图

图5　西北某风电场8月到10月风向玫瑰图

综上，风况是时变的、复杂多样的。单一预测模型无法体现风况时变性对风力发电过程的影响，导致预测误差低、模型适应性弱等问题。因此，根据风特征参数识别风场景，并据此划分风况类别，建立适用于复杂风况的概率预测模型是至关重要的，有助于提高风电功率预测精度和鲁棒性。

2数值天气预报误差敏感性分析

数值天气预报(NWP)是风电功率预测的基础数据，是预测误差的主要来源。国内外多数短期功率预测系统采用单一NWP源作为预测模型输入参量，国外也有采用多源NWP提高预测精度的工程实例。因此，研究NWP误差对风况的敏感性，对敏感性强的NWP风况进行细化分组，对不敏感的NWP风况进行集中归类，据此识别风场景，可以寻求预测精度和计算效率之间的平衡。

图6是不同NWP风速下的风速预测绝对误差，绝对误差平均值为0.045m/s，实线表示NWP风速预测的正误差和负误差的平均值，分别为0.78m/s和-0.6m/s。可见：当NWP风速较小时，风速预测绝对误差大多为负值；随着NWP风速增加，风速预测误差的绝对值减小；直至NWP风速为8m/s时，绝对误差达到最小值，将近为零。NWP风速继续增加时，风速预测的绝对误差持续增加，且预测数值向着大于实际风速的趋势发展。图7是NWP风速预测绝对误差的标准差，其平均值为2.03 m/s，在图中以实线表示。可见，风速预测绝对误差的标准差随NWP风速的增加而增加，即风速大的时候预测不确定性也相应增高，这种风速预测误差特性在非线性功率曲线的影响下对发电功率的影响更具不确定性。

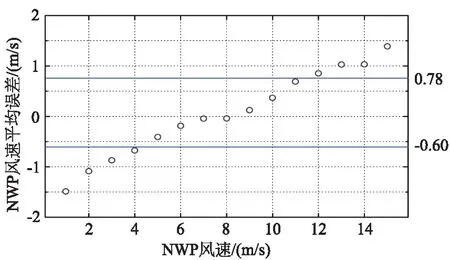
图6　NWP风速预测误差的平均值

图7　NWP风速预测误差的标准差

3基于K-means的风场景识别模型

K-means算法是聚类分析中应用最为广泛的一种无监督学习算法，具有算法简单、可高效处理大数据集的优点。该算法的基本思想是在给定聚类组数k值的条件下，通过多次迭代将n个样本数据分成k组[15-16]。聚类的目标函数为使聚类之后各组数据与所在组的聚类中心的距离总和最小。

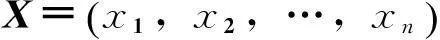
(1)

式中:‖xij-cj‖2为聚类样本点xij到第j组聚类中心cj的距离量度法；j为聚类组号。

K-means算法对于类内紧密、类间远离的聚类结构，具有较好的聚类效果。但必须事先给定聚类个数k值，另外该算法对孤立点较敏感，对于比较复杂的数据结构，聚类结果易受初始聚类中心选取的影响[17]。

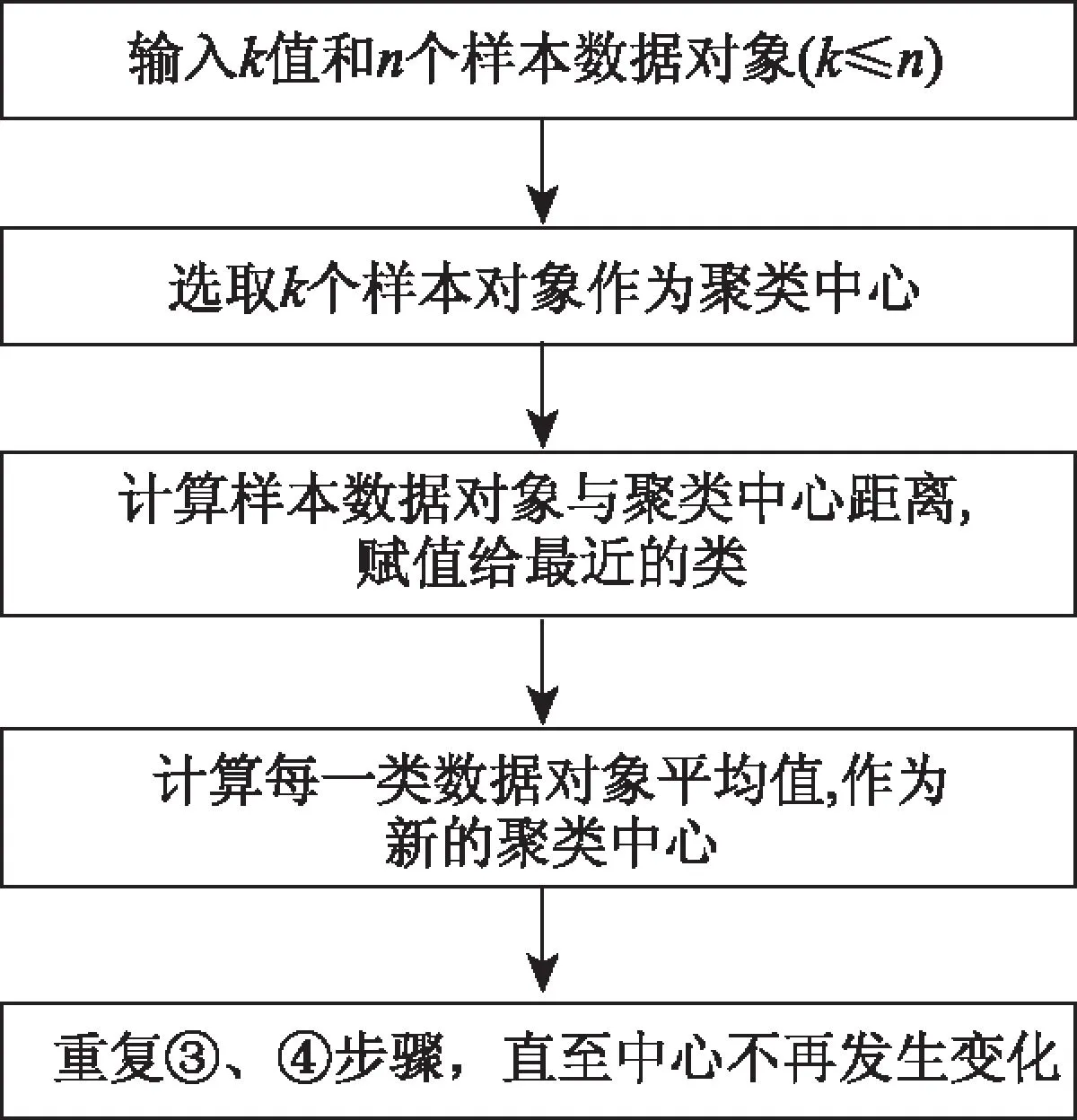
图8　K-means算法流程图

K-means算法流程见图8，计算步骤如下：

① 输入k值和待聚类的n个样本数据对象(k≤n)；

② 从原始数据对象中随机选取k个样本对象作为初始聚类中心；

③ 计算每个其他样本数据对象与各个类聚类中心的距离，将其赋给最近的类；

④ 计算每类数据对象的平均值，将其作为每一类新的聚类中心；

⑤ 重复步骤③、④，直至聚类中心不再发生变化，得到最佳聚类结果。

4相关向量机(RVM)原理[18]

假设yn为M个基函数φ(x)的线性权重加和：

(2)

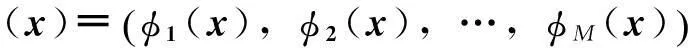
将核函数K(x,xi)引入相关向量机，得到预测公式：

(3)

式中:wi是权重向量；K(x,xi)是核函数； 概率定义如下式

(4)

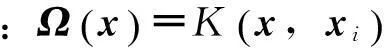
然后提出先验的概率分布

(5)

式中:α是超参数；N代表方差为σ2的高斯分布。定义了先验分布后，运用贝叶斯推理进行整理，关于未知数据的后验分布为

(6)

考虑到p(w|t,α,σ2)=∫p(t|w,σ2)p(w|α)dw为高斯的卷积形式，故权重值的后验分布为

(7)

式中:A=diag(α0,α1,…,αN)；

后验均值和方差分别为

(8)

(9)

计算上式关于α的偏微分，并令该式等于零，可得

(10)

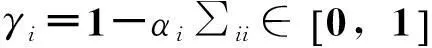
若样本数量为N，关于方差求微分，可得

(11)

在学习算法中，重复迭代式(9)和(10)，根据后验均值和方差式更新∑和μ，直到满足收敛条件为止。在参数估计过程中，大部分αi→，其对应的wi=0，导致大部分核函数矩阵的项不参与预测计算过程，大大降低了模型的复杂度和计算的时间。在超参数估计过程中，基于后验分布中各个权重值进行预测，不断调整最大化的。通过式(5)计算预测结果的分布，对于新数据x*进行预测：

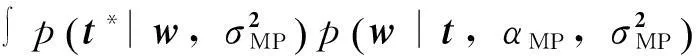
(12)

(13)

(14)

5动态概率预测模型

传统的概率预测方法是静态的、非条件性的，即不加区分地使用全部历史样本进行建模，无法代表每一特定时刻的“当前”状态，如：较小风速对应较小的输出功率，此种情况下的样本大多预测误差较小，使用这些样本建模，无法准确评估在预测较大功率时所面临的风险，这就需要建立考虑外部条件实时变化的、动态的概率预测方法。在风场景特征识别和类别划分的基础上，具有针对性地训练不同天气条件下的概率预测模型；在实际运行中，根据外界环境实时变化情况动态切换相应的预测模型。这种优化策略的优势是：一方面提高模型整体的精度和适应性；另一方面预计算训练模型，将大量耗时的模型训练放在实时预测之前进行，提高了模型运行的效率。

建模流程如图9所示，具体过程如下：

①将风速、风向数据输入K-means聚类模型，进行风场景识别和聚类分组；

② 针对风场景的分组结果，建立不同风场景类别下的训练样本和测试样本；训练样本包括：训练输入(NWP)和训练目标(实际功率)；测试样本包括：测试输入(NWP)和测试对照(实际功率)；

③ 利用各组别训练样本构建RVM预测模型(可参见文献[19]，具体计算步骤如下：

a.归一化处理：将所有的输入数据映射到[-1,1]的范围内；

b.计算后验分布的权重；

c.计算更新后验分布中的平均值和方差(或称变异数)；

d.迭代直至满足收敛条件；

e.反归一化处理。

④ 提取每一个风场景分组中的预测模型参数，以备预测时使用；

⑤ 实时预测中通过输入风速和风向实时判别当前风况所属的预测组别；

⑥ 调用相应模型参数预测风电功率及其波动区间。

图9　动态概率预测模型的建模流程图

6算例分析

6.1数据

以中国西北某风电场为例验证模型，运行数据包括12个月测风塔位置处的风速和风向，以及全场输出功率，时间分辨率为15min；数值天气预报数据包括风速、风向、气压、温度、湿度，数据的时间段和数据分辨率与运行数据相同。将数据分成两个部分，每个月前20d为训练样本，后10d为测试样本。与人工神经网络模型对比验证单点预测模型精度；与分位数回归模型对比验证概率预测效果。算例中各模型均采用相同的训练样本和测试样本，以保证对比的公平性。

6.2评价指标

采用两种主要的误差指标来评估单点预测精度：标准化均方根误差(NRMSE)和标准化平均绝对误差(NMAE)。NRMSE可以评估一段时期内的整体误差，而NMAE偏重代表系统实时偏差，计算公式见文献[20]。

采用文献[21]中的两个评价指标来验证不确定性分析模型，包括：可靠性指标和综合技术分数。可靠性指标是风电场实际功率落于预测区间内的概率与预设概率水平之间的差值，零为最优值。综合技术分数是综合评估可靠度和概率性波动区间大小的指标，数值越高模型越优，零为最优值。

6.3结果与分析

图10为基于K-means聚类算法的风场景识别结果，聚类组数设定为25，图中不同颜色代表不同类型的发电场景。可见，从功率曲线宽度轴来看，风场景划分较为均匀，说明实际功率曲线的分散性对误差影响模式较为固定；从风速轴来看，5～10m/s的风速段划分较细，这是因为功率曲线线性部分对误差影响较为灵敏；从风向轴来看，偏北方向的点比较密集，此为风电场主导风向。总之，风场景识别模型可对不同的风况(风速、风向)特征、功率曲线非线性特征进行有效地识别和分类。

图10　基于K-means聚类算法的风场景识别结果

图11为基于风场景识别的动态RVM模型在测试年内不同季节中随机4d的概率预测结果和实际功率曲线，设置置信水平为90%，即理论上概率预测的可靠性为90%。由图可见，单点预测曲线紧贴实际功率曲线且保持相同的走势；功率上下限与预测数值的趋势相同，实际功率曲线几乎全部在上下限范围内波动。经统计，动态RVM模型在测试年的NRMSE指标为13.27%，NMAE指标为10.79%；人工神经网络模型在测试年的NRMSE指标为14.53%，NMAE指标为11.27%；即RVM模型较人工神经网络NRMSE指标下降了9.47%，NMAE指标下降了4.44%。

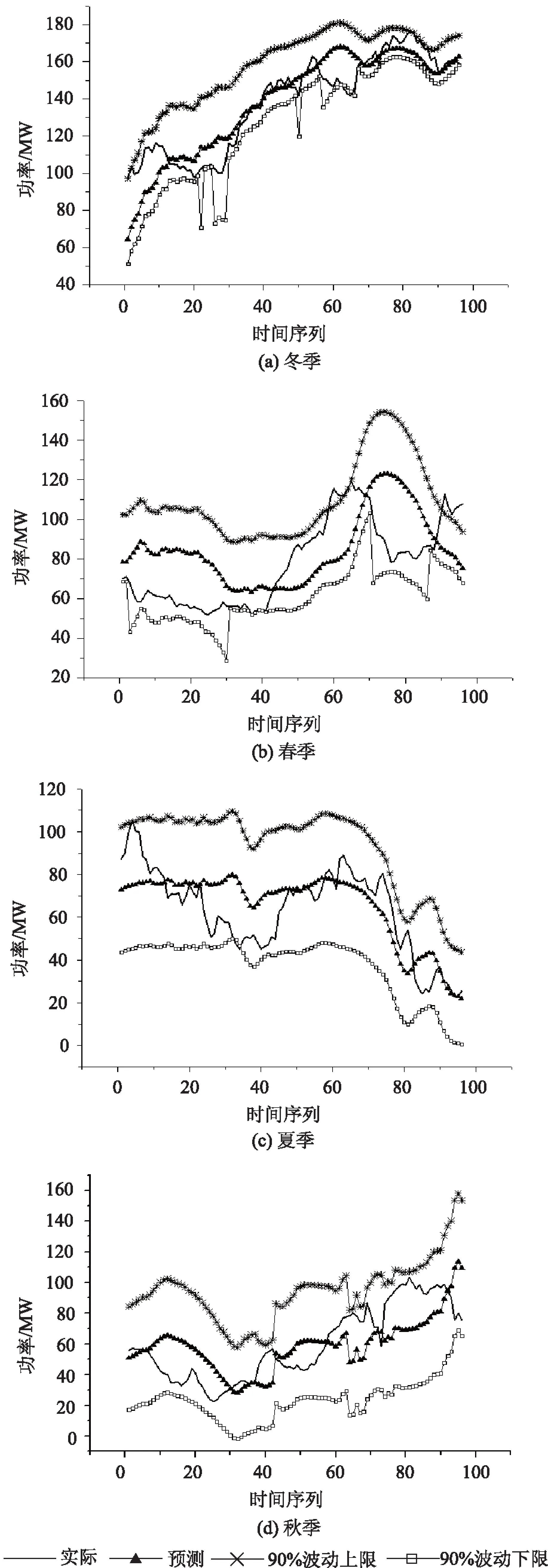
图11　各季节的实际功率曲线和预测功率曲线

图12为RVM动态概率预测模型与分位数回归模型的测试结果对比图。由图可见，动态RVM模型的可靠性指标为89.3%，分位数回归模型的可靠性指标为88.9%。两个模型的可靠性均非常接近置信水平的设置值，且动态RVM模型的可靠性比分位数回归方法稍高。对于综合技术分数，动态RVM模型比分位数回归模型高16.38%。

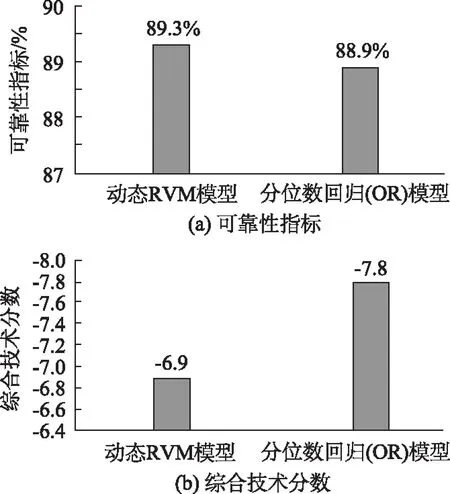
图12　RVM动态概率预测模型的测试结果

综上所述，基于风场景识别的风电功率概率预测模型的各个预测性能指标都有提升，说明该方法能够更有针对性地模拟不同的风场景下的发电过程，提高预测模型整体的鲁棒性和预测精度。当然，预测效果的提升不仅仅得益于风场景的划分，也得益于使用了映射能力更强的RVM算法。

任何预测模型都不可避免的具有误差和不确定性，通过敏感性分析研究气象参数(数值天气预报数据)对预测精度的影响，选取对预测结果影响较大的敏感参数进行细化建模，可以有效降低计算维度、进一步提高预测精度的目的。

将数值天气预报中的5个参量分别单独输入相关向量机概率预测模型，验证单一气象参量对预测效果的影响程度。如表1所示，风速是对预测结果影响最为主导的因素，年均方根误差为19%；风向的影响次之，均方根误差约为23%；其他因素影响效果均较小，均方根误差约为30%。可见，风电功率预测中至少要包括风速参量；使用风向参量在一定程度上可以提高预测精度，但提升程度需要进一步考察风电场的风向频率分布，以及机组分布位置；而其他气象参数并非必要的输入参量。同时，敏感性分析结果也间接验证了，将风速和风向作为风场景识别模型的输入参数是具有科学依据的。

表1　模型输入参量对预测误差的敏感性分析　%

7结论

本文提出了基于风场景识别的动态风电功率概率预测方法。利用K-means算法实现了对自然风变化和数值天气预报误差规律的特征提取以及聚类分析；利用相关向量机方法完成了对风电场输出功率的概率性预测，不仅提供功率单点预测数值，还计算任意置信水平下的功率波动范围。对耗费时间的模型训练过程进行预计算，在实时预测中仅需动态调用各类风况场景下的预测模型参数，为预测精细化建模提供了新的解决方案，有效提高了计算效率和预测精度。

以中国西北某风电场为例，对比不同预测模型的测试效果，结果表明：动态RVM模型相比人工神经网络模型降低了单点预测的年均方根误差和绝对误差，幅度分别为9.49%和4.44%；在概率性预测方面，动态RVM模型比分位数回归模型得到更为可靠的结果，且技术评分提高了16.38%。总之，该方法加强了对风况“当前”状态的识别和模拟，有效提高了预测的鲁棒性和精度；且具有较强的实时预测能力。

参考文献

[1]2014年中国风电装机容量统计.中国风能协会.

[2]刘永前,韩爽,胡永生. 风电场出力短期预报研究综述[J]. 现代电力, 2007(5):6-11.

[3]牛东晓,范磊磊. 风电功率预测方法综述及发展研究[J]. 现代电力, 2013(4): 24-28.

[4]Mabel M C,Fernandez E. Analysis of wind power generation and prediction using ANN: a case study [J]. Renewable Energy, 2008, 33(5): 986-992.

[5]Cadenas E, Rivera W. Short term wind speed forecasting in La Venta, Oaxaca, México, using artificial neural networks [J]. Renewable Energy, 2009, 34 (1): 274-278.

[6]Tu Y L, Chang T J,Chen C L, et al. Estimation of monthly wind power outputs of WECS with limited record period using articial neural networks [J]. Energy Conversion and Management, 2012, 59: 114-121.

[7]Rasit Ata. Articial neural networks applications in wind energy systems: a review [J]. Renewable and Sustainable Energy Reviews, 2015, 49: 534-562.

[8]Bremnes J B. Probabilistic wind power forecasts using local quantile regression [J]. Wind Energy, 2004, 7(1): 47-54.

[9]阎洁,刘永前,韩爽. 基于分位数回归方法的风电功率预测不确定性分析[J]. 太阳能学报, 2013, 34(12): 2101-2107.

[10]Haque A U, Nehrir M H, Mandal P. A Hybrid Intelligent Model for Deterministic and Quantile Regression Approach for Probabilistic Wind Power Forecasting [J]. IEEE Transactions on Power Systems, 2014, 29(4): 1663-1672.

[11]Bessa R, Miranda V, Botterud A, et al. Time Adaptive Conditional Kernel Density Estimation for Wind Power Forecasting [J]. IEEE Transactions on Sustainable Energy, 2012, 3(4): 660-669.

[12]Taylora J W, Jeonb J. Forecasting wind power quantiles using conditional kernel estimation [J]. Renewable Energy, Aug. 2015, 80: 370-379.

[13]Wang J, Botterud A,Bessa R, et al. Wind power forecasting uncertainty and unit commitment [J]. Applied Energy, 2011, 88(11): 4014-4023.

[14]Aghaei J, Niknam T, Azizipanah-Abarghooee R, et al. Scenario-based dynamic economic emission dispatch considering load and wind power uncertainties [J]. International Journal of Electrical Power & Energy Systems, May, 2013, 47: 351-367.

[15]Kanungo T, Mount D M, Netanyahu N S, et al. An efficientK-means clustering algorithm: analysis and implementation [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2002, 24: 881-892.

[16]Wagstaff K, Cardie C,Rogers S, et al. ConstrainedK-means clustering with background knowledge [C]. Proceedings of the 18th International Conference on Machine Learning, 2001: 577-584.

[17]周世兵,徐振源,唐旭清.K-means 算法最佳聚类数确定方法[J].计算机应用, 2010, 30(8): 1995-1998.

[18]Tipping M E. Sparse Bayesian Learning and the Relevance Vector Machine[J]. Journal of Machine Learning Research, 2001(1):211-244.

[19]Yan J, Liu Y Q, Han S, et al. Wind power grouping forecasts and its uncertainty analysis using optimized relevance vector machine [J]. Renewable & Sustainable Energy Reviews, 2013, 27: 613-621.

[20]Shuafiu A, Anaya-Lara O, Bathurst G. Aggregated wind turbine models for power system dynamic studies [J]. Wind Engineering, 2006, 30(3):171-185.

[21]Pinson P, Nielsen Haa, Møller J K, et al. Nonparametric probabilistic forecasts of wind power: required properties and evaluation [J]. Wind Energy, 2007, 10: 497-516.

阎洁(1987-)，女，博士研究生，风电场功率预测及不确定性分析、含有风电的电力系统优化运行等， E-mail:yanjie_freda@163.com；

刘永前(1965-)，男，教授，博士生导师，研究方向为风电场设计与运营技术等，E-mail:yqliu@ncepu.edu.cn。

(责任编辑：林海文)

摘要：传统风电功率预测是确定的、静态的、非条件性的，无法代表不同外部状态的发电过程，缺失预测误差的概率性信息。针对上述问题，提出了一种动态的基于风场景识别的风电功率概率预测方法。首先建立基于K-means的风场景识别模型，根据风速和风向识别自然风特征，据此划分风电场风况类别。然后针对各风况类别建立基于相关向量机的概率预测模型。在实际预测中，根据实时风况动态调整概率预测模型参数。以中国西北某风电场为例进行验证，结果表明，该方法提高了单点预测精度、概率预测可靠性和技术分数、运行效率，为预测细化建模提供新的解决思路。

关键词：风场景;动态预测;风电场;概率预测;细化建模

Abstract：Most traditional wind power forecasting methods are deterministic and static without considering external changing conditions as well as probabilistic information of forecasting error. To solve the above problem, a new wind power probabilistic forecasting method is presented based on wind scenario recognition in this paper. Firstly, a wind scenario recognition model is established based on K-means clustering algorithm. The natural wind feature is extracted from wind speed and wind direction. Then, the probabilistic forecasting models based on relevance vector machine (RVM) are built for each wind scenario. During real-time forecasting, the power generation process in different conditions can be recognized and mapped by adjusting the parameters of the pre-established probabilistic forecasting model. Taking a wind farm in Northwest China as an example, the results show that the accuracy of deterministic forecasting, the reliability and skill score of probabilistic forecasting, and forecasting efficiency are improved by the proposed method, which provides a new solution for refined forecast modeling.

Keywords：wind scenario; dynamic forecasting; wind farm; probabilistic forecasting; refined modeling

作者简介：

收稿日期：2015-04-02

基金项目：国家自然科学基金(51206051)；国家电网公司科技项目

中图分类号：TM614

文献标志码：A

文章编号：1007-2322(2016)02-0051-08