一类特殊本原有向图的m－competition指数

李林倩,方 炜

（1.山西农业大学信息学院,山西晋中030800；2.中北大学仪器与电子学院,山西太原030051）

一类特殊本原有向图的m－competition指数

李林倩1,方 炜2

（1.山西农业大学信息学院,山西晋中030800；2.中北大学仪器与电子学院,山西太原030051）

对一类含有两种不同圈长的本原有向图的m－competition指数进行了研究,根据图论知识,通过分析本原有向图D与本原有向图Dn－4,Dn－2之间的关系,结合本原有向图m－competition指数的定义,利用集合的运算给出了此类图的m－competition指数.

本原有向图；途径；m－competition指数

0 引言

设D为有向图,顶点集为V（D）,边集为E（D）,D中允许有环但不允许有重弧.本原有向图的研究,最早始于1950年Wielandt的工作,他给出了n阶本原有向图的一般性上界.文献［1,2］中介绍了本原有向图的定义,设D为有向图,如果存在正整数k,使得对于D中的任意两个顶点vi,vj（可以相同）,在D中都存在从vi到vj的k长途径,则称D为本原有向图.上述最小的k称为D的本原指数,记为exp（D）.

文献［3］中,M.Akelbek和S.Kirkland给出了本原有向图的scrambling指数的定义.D是n阶本原有向图.如果存在正整数k,对于D中任意顶点vi和vj,都存在顶点w∈V（D）,使得从vi和vj到w都有k长途径,满足上述条件的最小正整数k称为本原有向图D的scrambling指数,记作k（D）.

文献［4］中,从记忆通讯系统的背景,柳伯濂和黄宇飞对scrambling指数进行了推广,引入了广义scrambling指数.设D为n阶本原有向图,λ,μ∈Z＋,1≤λ,μ≤n.对于集合X⊆V（D）,定义（D）为最小的正整数l,使得存在μ个顶点w1,w2,…,wμ∈V（D）,对于∀x∈X,从x到wi都有l长途径（i＝1,2,…,μ）,则

分别称为本原有向图D的λ重下μ－scrambling指数和λ重上μ－scrambling指数.

本原有向图的m－competition指数是本原指数与scrambling指数的推广.文献［5］中,Hwa Kyung Kim和Sung Gi Park给出了本原有向图的m－competition指数的概念.设D为n阶本原有向图,1≤m≤n,对于任意的顶点u,v∈V（D）,存在正整数m,在D中总能找到m个点,使得u,v到这m个点都存在k长途径,上述k的最小值称为D的m－competition指数,记作km（D）.m－competition指数也称为广义competition指数.

另外,根据三者定义不难得到n阶本原有向图的m－competition指数与本原指数,scrambling指数之间的关系：k（D）＝k1（D）≤k2（D）≤…≤kn（D）＝exp（D）.

为了表达方便：

2）RDt｛x｝表示从集合D中的顶点x出发,经过t长途径所能到达的点的集合,t为非负整数.

3）｜RDt｛x｝｜表示从集合D中的顶点x出发,经过t长途径所能到达的点的个数.

1 主要结论

本文主要主要研究了一类特殊的本原有向图D（含有两个n－4圈和一个n－2圈,如图1所示）的mcompetition指数见图1,图2.

图1D

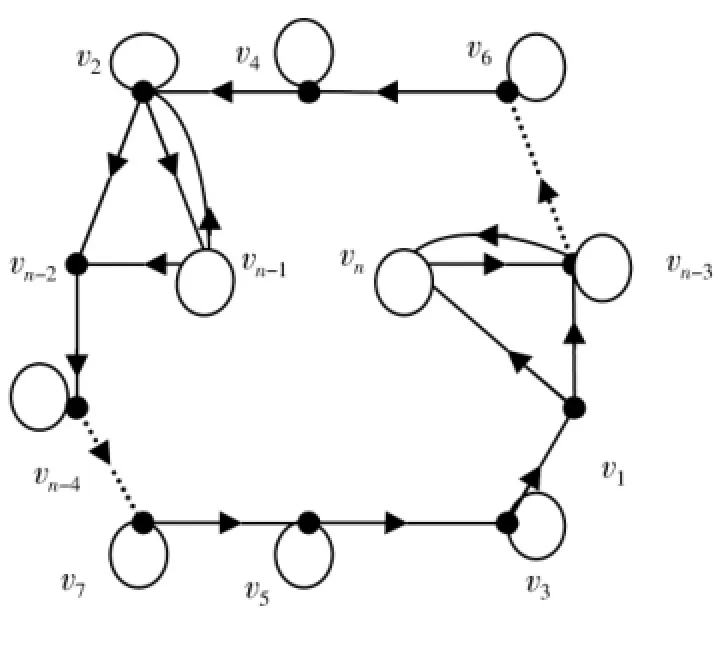
图2Dn－4

定理设D为n（n≥9,n≡1（mod2））阶本原有向图（如图1所示）,则有向图D的m－competition指数为：

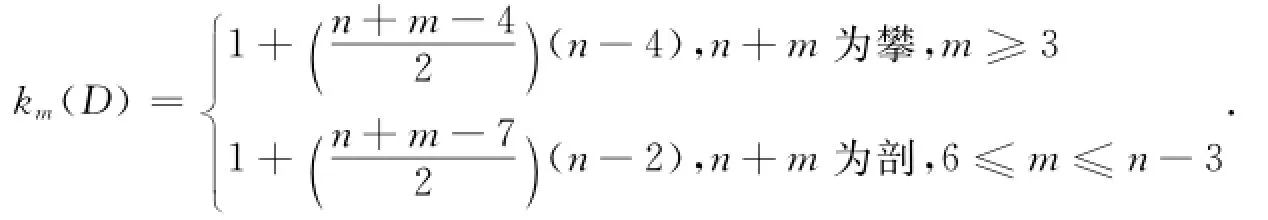
证明：Case1n＋m是偶数,且m≥3.

由D的本原性可得Dn－4（如图2所示）是本原的.

在Dn－4中,令Cn－2＝｛v1,v2,…vn－3,vn－2｝,其中｛v2,v3,…vn－3｝是环点.当vi是环点时,从vi经过长途径所能到达的点的个数至少为

图3Dn－2

Case2n＋m是奇数,且6≤m≤n－3.

由D的本原性可得Dn－2（如图3所示）是本原的.

在Dn－2中,令Cn－4＝｛v2,v3,…vn－3｝,且Cn－4中的顶点都是环点.当vi是环点时,从vi经过n长途径所能到达的点的个数至少为

在D中,点集V（D）＼｛vn－2,vn－3｝中的任意一个顶点经过1长途径都能到达环点｛v2,v3,…vn－3｝,而且

［1］邵嘉裕.对称本原矩阵的指数集［J］.中国科学（A辑）,1986（9）：931－939

［2］徐俊明.图论及其应用［M］.第2版.北京：中国科学技术大学出版社,2005

［3］Mahmud Akelbek,Steve Kirkland.Coefficients of ergodicity and the scrambling index［J］.Linear Algebra and its Applications,2009,430：1111－1130

［4］Yufei Huang,Bolian Liu.Generalized scrambling indices of a primitive digraph［J］.Linear Algebra and its Applications,2010,433：1798－1808

［5］Hwa Kyung Kim.Generalized competition index of a primitive digraph［J］.Linear Algebra and its Applications,2010,433：72－79

The Competition Index of A Special Class of Primitive Digraphs

LI Linqian1,FANG Wei2
（1.College of Information,Shanxi Agricultural University,Jinzhong 030800；2.School of Instrument and Electronic,North University of China,Taiyuan 030051,China）

A class of two different cycle length of primitive digraphs are discussed.According to graph theory,by analyzing the relationship between the primitive digraph D and the primitive digraphDn－4,Dn－2and combining with the definition of the m－competition index of a primitive digraph,the exponent of this special class of primitive digraphs is given through the set operations.

the primitive digraph；walk；m－competitionindex

1672－2027（2016）04－0045－04

O157.5

A

2016－09－11

李林倩（1987－）,女,山西长治人,硕士,山西农业大学信息学院助教,主要从事组合数学的研究.